柔性作业车间中基于工序分批的调度问题与求解
徐本柱 吉 靖 费晓璐
合肥工业大学,合肥,230009
柔性作业车间中基于工序分批的调度问题与求解
徐本柱 吉 靖 费晓璐
合肥工业大学,合肥,230009
考虑到柔性作业车间分批调度中不同工序具有各自合适批量大小,提出了基于工序分批调度的概念,建立了以关键路径工序为中心的分批调度模型。该模型动态更新可加工工序子批集,同时更新可选加工机器,及时调整加工路线,为不同工序安排大小合适的批量,以达到优化完工时间、有效降低总加工批次的目的。实验结果表明,相比基于工件分批的调度,该模型在优化最长完工时间、提高机器利用率的同时,大幅减少了总加工批次数量(42%),降低了车间调度管理的复杂度。
柔性作业车间;分批调度模型;工序分批;不等量分批
0 引言
作业车间调度问题(job-shopschedulingproblem,JSP)是一类满足任务分配和顺序约束的组合优化问题[1],随着实际作业车间模式的不断改革创新和研究的不断推进,分批和并行成为JSP的重点扩展方向[2-3]。并行机调度问题(PMSP)和流水作业车间调度问题(FSSP)是作业车间调度研究的典型问题,文献[4]利用差分进化算法分别对并行机调度问题和流水作业车间调度问题进行了分批调度优化。文献[5]利用蚁群算法对混合流水作业车间调度问题,即并行机调度和流水作业车间调度的结合问题,进行了分批调度优化。而柔性作业车间调度问题(flexiblejob-shopschedulingproblem,FJSP)作为JSP的扩展[6],是目前调度领域的重要研究方向。当前柔性作业车间分批调度问题(flexiblejob-shopschedulingwithlot-splittingproblem,FJSLP)模型对同种工件所有工序采用等量分批的方法,没有考虑不同工序的适合批量需求。由于不同工序具有加工时间、加工准备时间和约束关系不同等特点,使得不同工序具有各自的合适批量大小,甚至同一工序在不同机器上加工,其合适的批量大小也可能会发生变化。
作为并行加工问题重要的优化方法,分批调度一直是国内外针对柔性作业车间调度研究的热点。文献[7-8]通过仿真实验证明分批处理可以有效提高机器利用率,缩短生产周期,但并未给出具体的分批方法。文献[9]解决了单一工艺路线的作业车间分批调度问题,但未考虑柔性作业车间的调度环境。文献[10]提出了一种等量分批方法,该方法使子批批次数量的确定和子批加工顺序的确定同时得到优化,但由于是等量划分,各子批批量难以根据设备的负荷大小进行柔性调整。文献[6]利用压缩技术,设计了一种动态柔性分批策略,使得工件可以根据设备负荷动态调整批量大小。文献[11]利用遗传算法解决FJSP问题,有效地优化了最长完工时间,但是该算法存在早熟、收敛慢的缺点。文献[12]利用两级遗传算法解决可变工艺路线的JSP问题。文献[6]利用禁忌搜索法解决柔性作业车间分批调度问题,对分批策略进行优化,并在优化加工顺序的过程中提出对关键路径进行邻域搜索的方法,可以有效地平衡机器负荷,缩短生产周期。但是面对多品种小批量的生产需求,以上文献没有考虑变批量的生产特征。文献[13-14]针对多品种、变批量需求的可重构制造问题,综合考虑工艺路线与生产批量约束关系,提出了两阶段求解的虚拟制造单元构建方法。但上述方法没有考虑到工序具有加工时间不同、准备时间不同以及工序约束关系不同等特点,本质上都属于基于工件分批的方法。
本文针对柔性作业车间中不同工序的加工工时及准备时间不同、工序间约束关系差异的情况,以及各工序合适的批量大小不尽相同的特点,提出了基于工序分批的调度概念,建立了以关键路径工序为中心的分批调度模型。该模型为不同工序安排了合适的批量大小,同时优化了最大加工完成时间,大幅减少了加工批次数量,并且使得分批更加灵活,符合实际生产需求。
1 问题描述
本文重点研究柔性作业车间工件工序可并行的分批调度问题,即在柔性作业车间调度的基础上对工序进行分批,为不同的工序安排合适的批量,并让受约束不可同时加工的工序在一定条件下并行加工,该分批调度问题描述如下:共有n种待加工工件J= {Ji|i=1,2,…,n},在m台加工机器M= {Mk|k=1,2,…,m}上进行加工,工件Ji包含ni道工序,工序集合为O={Oij|i=1,2,…,n;j=1,2,…,ni},每道工序可在多台机器上进行加工,同一工序在不同的设备中加工时间相等或不等,每种工件的每道工序被分成l= {lij|i=1,2,…,n;j=1,2,…,ni}个批次。
图1所示为工件P的加工工序,若基于工件分批,则批次数量lP1=lP2=lP3,即所有工序批次数量相同,而本文基于工序分批,则lP1、lP2、lP3根据工序特点进行确定,可相等或不等。

图1 工件P的加工工序
针对上述问题描述,假设如下:①所有工件的工序数以及工序约束关系已知;②每道工序在可用机器上的加工时间确定;③每道工序加工准备时间已知;④加工过程中设备不因人为或非人为因素中断。
同时,该问题需要满足以下约束:①加工设备约束。同一机器在完成一个批次的工件后才能加工另一个批次。②加工准备时间约束。同工件相同工序的不同批次依次在同一机器上进行加工,后者无需加工准备时间,其他情况则需要加工准备时间。③工序并行性约束。在工件的加工装配过程中,工件的某些工序可以并行加工。如图2和图3所示:图2中,子工件A经过工序OA加工成子工件A′,子工件B经过工序OB加工成子工件B′ ,子工件A′ 和B′经过工序OC加工成目标工件C,图3是图2抽象出的工序约束关系图。工序并行性约束存在两种情况:相同批次的工序OA和工序OB可并行加工;不同批次的工序OA和工序OC可并行加工。④工序子批批量动态加工约束。每道工序所有紧前工序已加工总批量需大于或等于该道工序的欲加工子批批量,此工序批次方可加工。
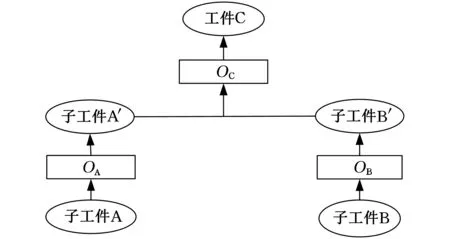
图2 工件工序加工装配图

图3 工序约束关系图
2 基于工序的分批调度模型
根据问题的描述和实际需要,建立数学模型,目标函数如下。
(1)设Ci为工件Ji的完工时间,下式表示最长完工时间最小:
(1)
(2)设lij为工序Oij的被划分的批次数量,下式表示总加工批次最少:
(2)
本文属于多目标求解问题,在优化f1的同时,尽可能减小f2,以降低车间管理复杂度。
批量加工相关的约束条件如下。
(1)设Xijz为工件Ji第j道工序第z批的批量大小,Di为工件Ji的总数量,同工序的所有批次数量总和等于工件总数。故批次数量和批量大小间的约束关系如下:
(3)
(2)同一工序内采用等量分批的方法,当工件不可完全等分时,剩余不足一批的工件与前一批次同时加工。设lij为工件Ji第j道工序的批次数量,则子批大小为
(4)
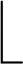
(3)所有工序间批次数量可相等,也可不等。因此不同工序间批次数量关系约束如下:
lij=lij′‖lij≠lij′j≠j′
(5)
(4)同一台机器,当欲加工批次的工序与紧前加工批次工序不同时,需要加工准备时间,否则无需加工准备时间。设pijk为工件Ji第j道工序在机床Mk上加工单个工件的时间,prijk表示工件Ji第j道工序在机床Mk上的加工准备时间,cijzk表示工件Ji第j道工序的第z批次在机床Mk上的全部加工时间。工件工序单批次的加工时间约束如下:
(6)
(5)设psijzk为工件Ji第j道工序第z批次在机床Mk上的加工开始时间,ei′j′z′k为第i′ 种工件第j′ 道工序的第z′ 批次在机床Mk上的加工结束时间。设备Mk在完成对正在加工批次所有工件的加工之后,才能进行下一工序批次的加工。即批次加工不可中断约束如下:
psijzk≥ei′j′z′k
(7)
式中,z′为z的紧前批次。
3 基于工序的分批调度算法
3.1 确定调度工艺路线
3.1.1 工艺路线的表示方法
当前生产模式越来越趋向于加工装配混合进行。针对实际作业车间工件加工的分解与合成,本文采用加工顺序树[15]对这种生产加工过程进行形象描述。
加工顺序树是产品的一种工艺结构表示形式,如图4所示,树的节点表示工序,有向边是工序加工的顺序约束关系,所以叶子节点是最先可以被加工的工序,根节点是最后加工的工序。工件i的加工顺序树每个节点的表示形式为Oij/lij/Mj1,Mj2,…,Mjx/pj1,pj2,…,pjx。其中,Oij为工件i的第j道工序;lij为工序Oij的批次数量;Mj1,Mj2,…,Mjx为工序Oij的可选设备;x表示工序Oij在该时刻有x台可选加工设备;pj1,pj2,…,pjx为工序Oij在不同设备上对应的加工时间。
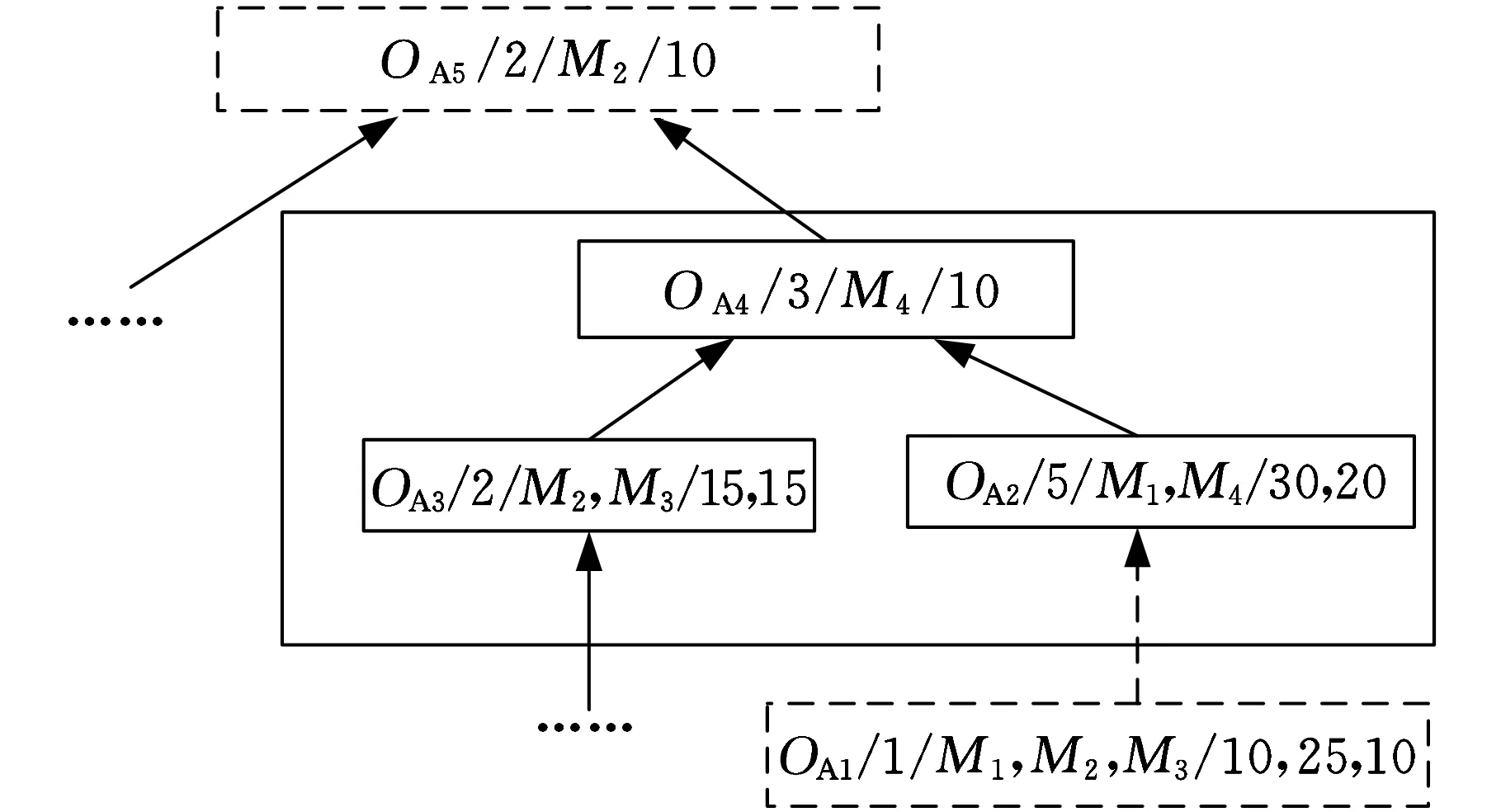
图4 工件A的部分工序加工顺序树
3.1.2 可加工工序子批集确定方法
本文定义可加工工序子批集σjob包含当前可加工的所有工序子批,该集合随着工序子批加工的进行而动态变化,以工件A为例。图4给出了工件A的部分工序加工顺序树,加工数量为100,共有4台加工设备。假设工序OA2和OA3的所有前驱工序都加工完毕,执行图4框中的工序步骤。
根据图4,当前阶段工序OA2被分为5批,工序OA3被分为2批,工序OA4被分为3批。则当前可加工工序子批集σjob为{OA2-1,OA2-2,OA2-3,OA2-4,OA2-5,OA3-1,OA3-2},可加工工序子批集的动态更新过程如下。
(1)随机选择加工工序OA2-1,数量为20。
(2)OA2-1加工完成,判断OA2-1紧后工序OA4-1可否被加工。加工OA4-1需要满足条件1({33个OA2加工完成的半成品})和条件2({33个OA3加工完成的半成品}),条件1和条件2均不满足。
(3)加工OA2-2,数量为20,总加工数量为40。
(4)OA2-2加工完成,判断OA2-1紧后工序OA4-1可否被加工,条件1满足,条件2不满足。
(5)加工OA3-1,数量为50。
(6)判断OA3-1紧后工序OA4-1可否被加工,条件1和2均满足,触发OA4-1进行加工,更新可加工工序子批集为{OA2-3,OA2-4,OA2-5,OA3-2,OA4-1}。
根据上面描述的某阶段加工工序子批集动态变化过程,给出确定加工工序子批集的方法。
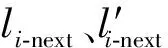
(8)
化简上式可得不可加工子批工序变为可加工工序的判定公式:
(9)
3.1.3 机器以及加工顺序确定方法
在加工开始阶段,所有机器都是空闲的,可加工工序子批集σjob中的所有工序在对应可选设备中均可以加工。如果在某个机器空闲时刻只有一道工序可在该机器上加工,那么该道工序选择在该空闲机器上加工;如果某时刻没有工序可以在该机器上加工,则机器处于空闲状态,直到某可加工工序加工完成后,不可加工工序转化为可加工工序,更新可加工工序子批集,再对机器进行选择;如果在某一时刻存在多个工序对一台空闲机器M1进行争夺,分下面三种情况进行讨论。
(1)存在2道或以上的工序争夺机器M1,且其可选设备只有M1。假设某时刻T空闲机器为M1,有两道工序O1(M1)、O2(M1),即O1、O2同时争夺空闲机器M1,利用机器短用时策略[15]为M1选择可加工工序,即选择加工时间较短的工序进行加工。
(2)争夺机器M1的所有工序均存在多个可选设备(包括M1在内)。假设某时刻T空闲机器为M1,有两道工序O1(M1,Mi, …,Mx)和O2(M1,Mj, …,My)同时争夺M1,工序O1在M1上的加工时间为p11,O2在M1上的加工时间为p21,同样选择加工时间较短的工序进行加工。
(3)争夺机器M1的多个工序中,有且仅有一道工序,其可选设备唯一,即M1。假设某时刻T空闲机器为M1,有两道工序O1(M1,Mi, …,Mx)和O2(M1),工序O1加工时间为p11,O2加工时间为p21,(Mi, …,Mx)结束当前加工工序时间为(ei, …,ex),那么判断max(ei, …,ex)与T+p21:若max(ei, …,ex)>T+p21,如图5所示,那么当前空闲机器加工工序O2;若max(ei, …,ex)
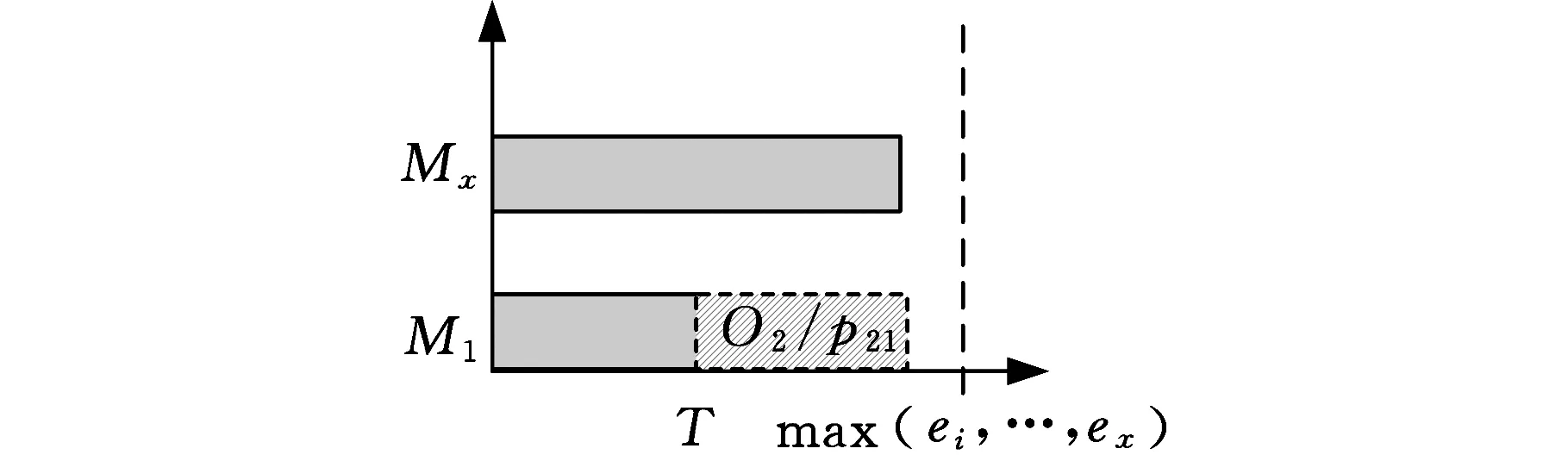
图5 max(ei,…,ex)>T+p21甘特图
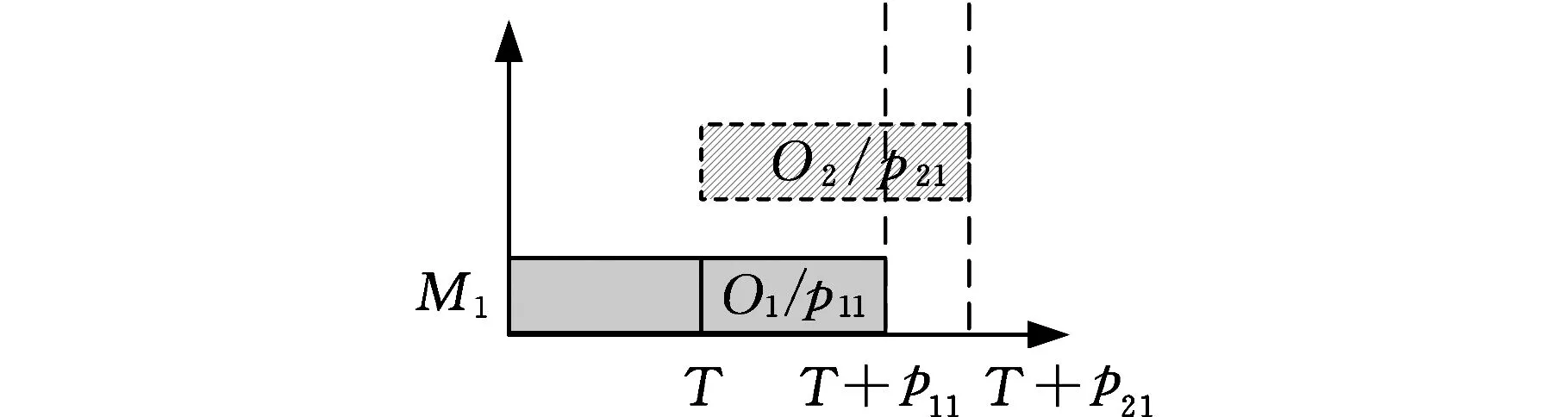
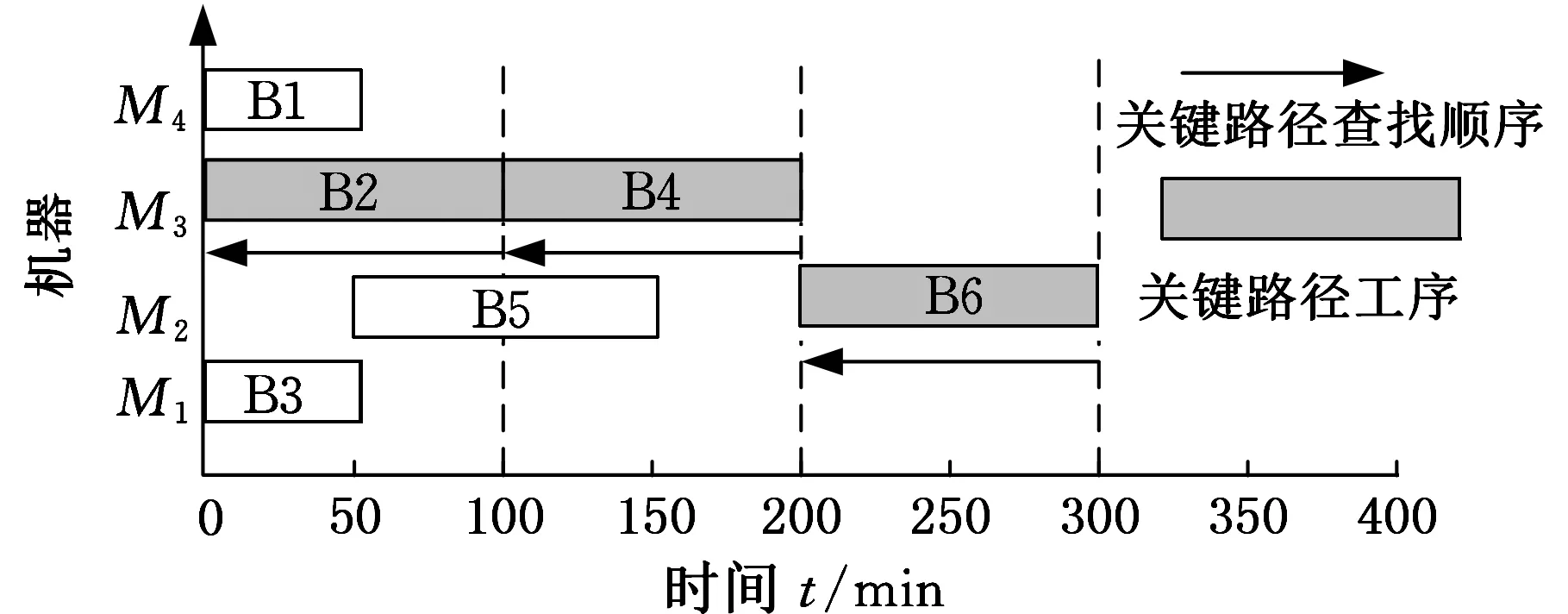
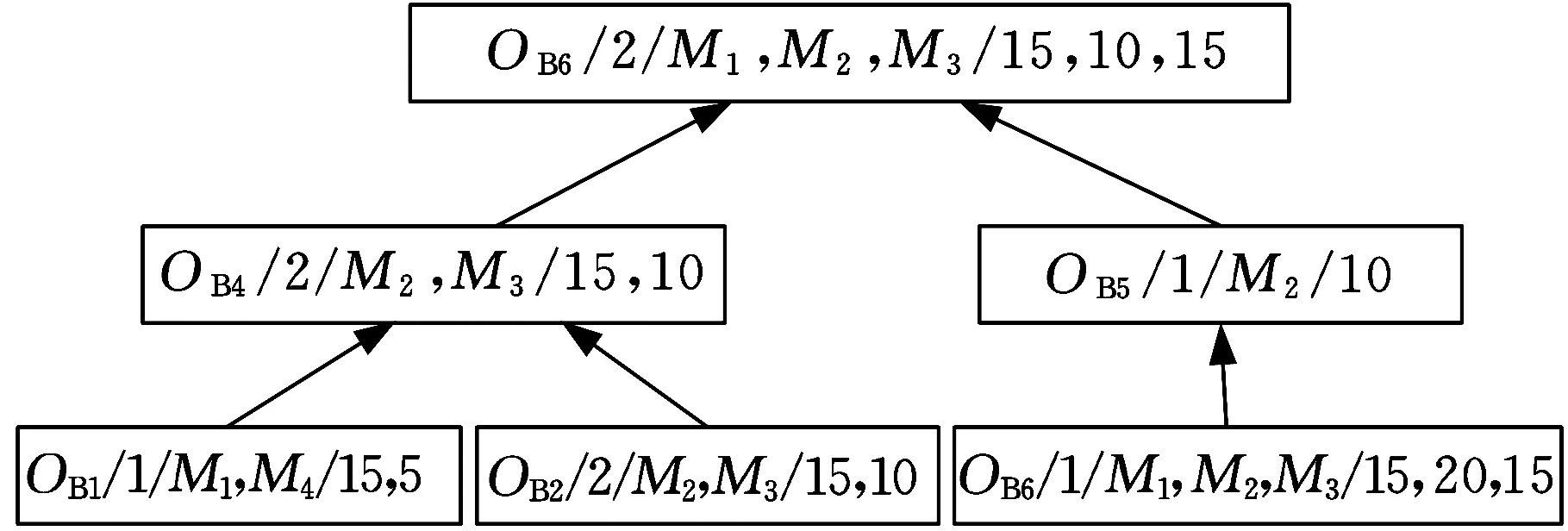
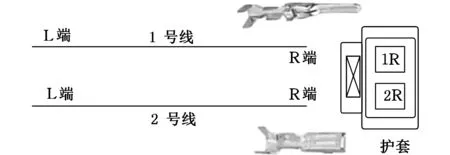
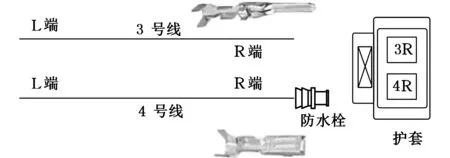
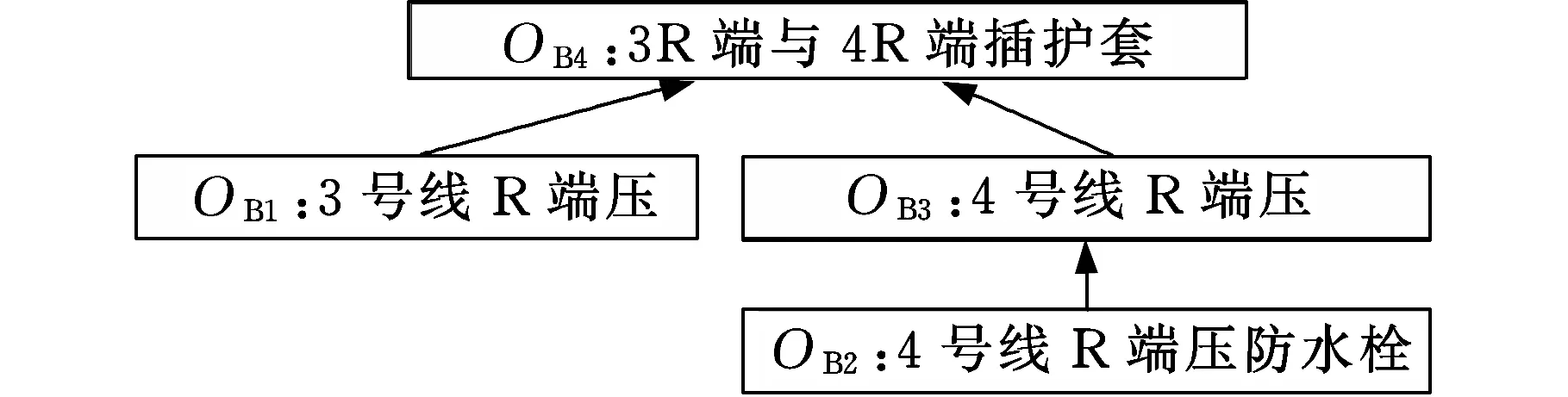
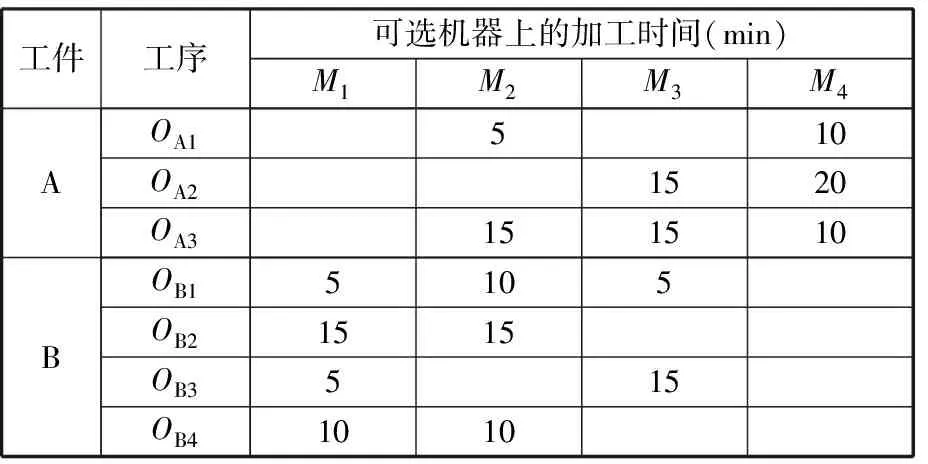
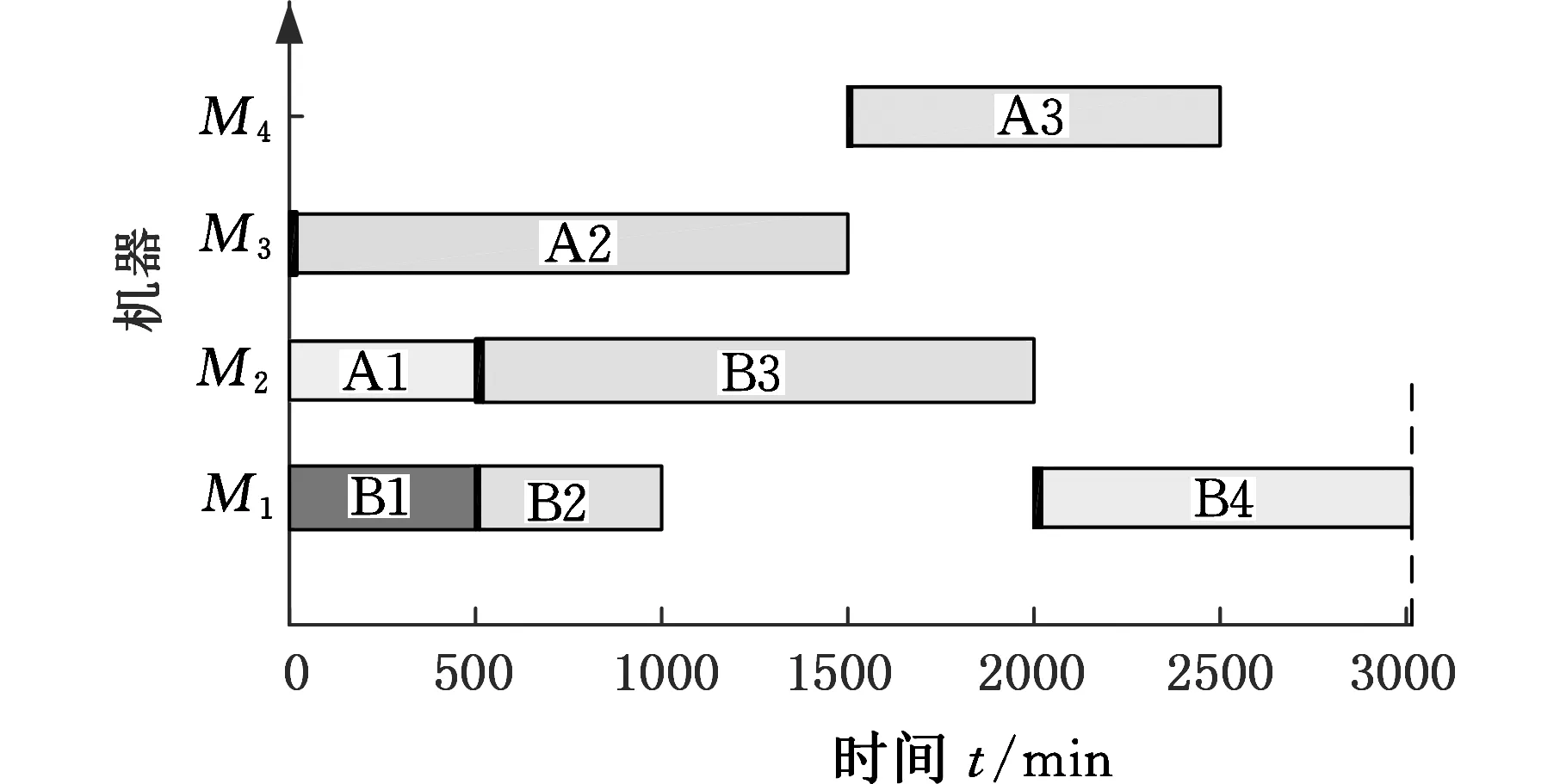
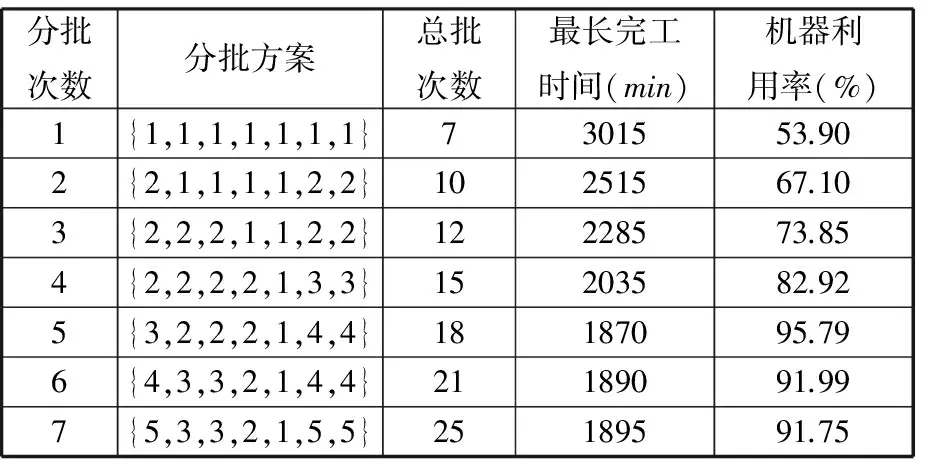
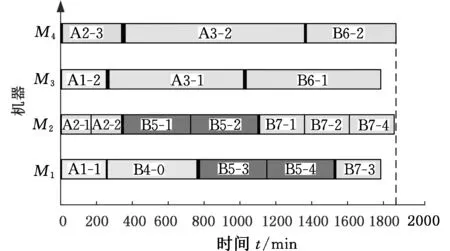
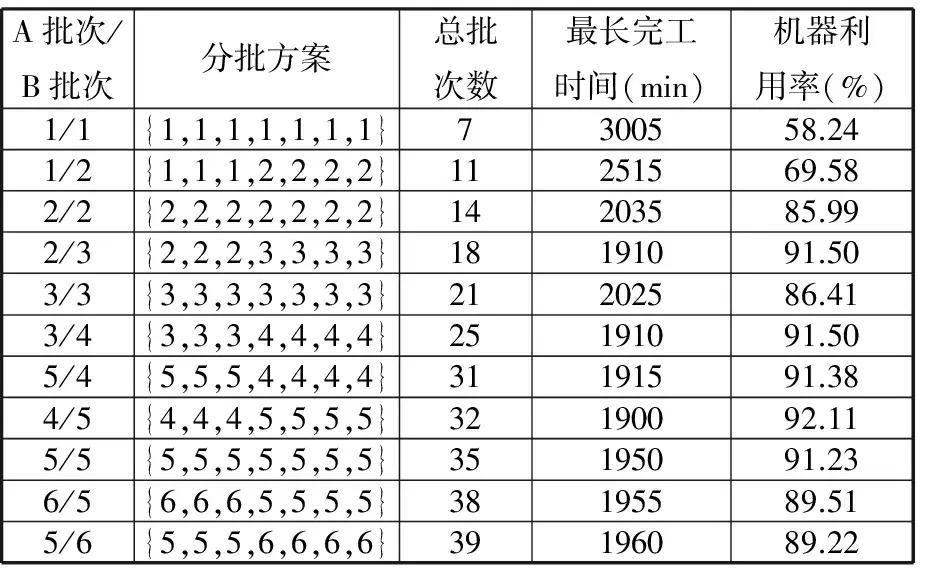
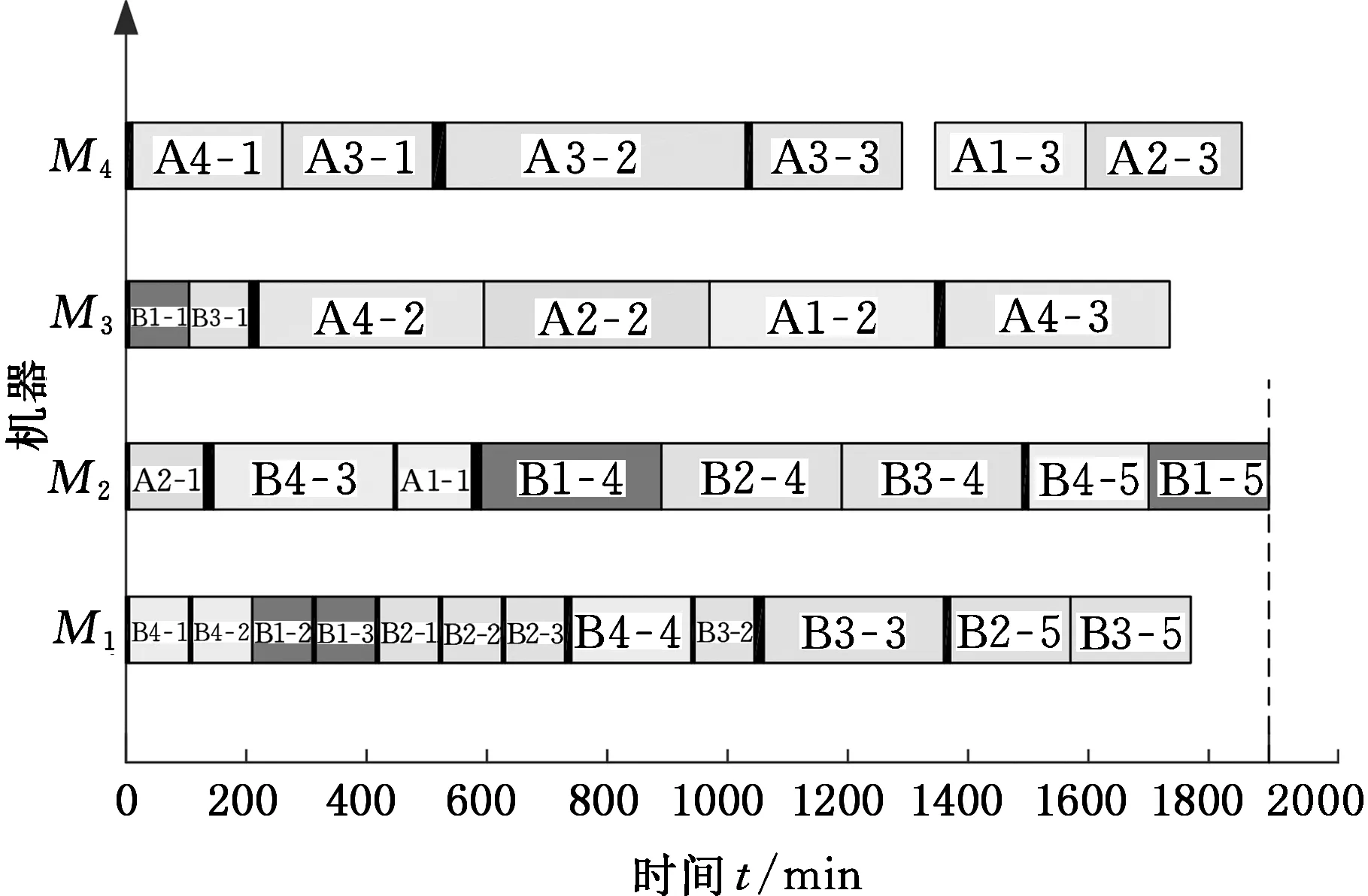
图6 max(ei, …, ex) 针对以上三种情况,如果争夺机器工序加工时间相同,则使用长路径策略[16]选择加工工序。 长路径策略即选择比工序父节点的最短加工路径长度更长的工序进行加工。最短路径长度为根节点到可加工节点之间的最短加工路径长度。计算过程中,因为每道工序的加工机器不唯一,加工时间不同,所以选择最短的加工时间作为最短路径时间。假设有两道工序Ox和Oy在一台空闲机器上的加工时间相同,工序Ox、Oy的最短加工路径长度分别为Lx和Ly,根据长路径策略,若Lx>Ly,那么加工Ox,反之则加工Oy。文献[17]指出,优先加工路径长度更长的工序,可以使两个可调度工序及其后续工序的总加工时间减少,实现工序加工的最大并行性。 3.2 关键路径工序的分批算法 根据上述方法确定加工工艺路线,在工艺路线中,加工时间最长的路径为关键路径[6],由于对关键路径有效的调整对产品的加工时间有很大程度的影响[18],所以本文对批量的调度研究也应用了关键路径。 首先确定工件加工任务中的关键路径,从最后完工的某一工序开始搜索首尾相连的工序(同时遇到其紧前工序和同一机器前邻工序时取其机器前邻工序)得到一条关键路径[19],关键路径工序子批集σkey由关键路径上所有工序子批组成。给出关键路径工序分批算法步骤如下。 (1)根据调度策略及方法生成整批调度路线Rfull。 (2)整批调度路线作为当前最新调度路线和最优调度路线:Ropt=Rnew=Rfull。 (3)确定Rnew的关键路径以及关键路径工序子批集σkey。 (4)σkey中的工序批次数量:lσ←lσ+1,非关键路径工序子批数不变。 (5)判断σkey中最大的分批数与给定的分批最大值llimit的大小:若maxlσ>llimit,则分批结束并返回最优调度路线Ropt;否则,继续步骤(6)。 (6)对所有工序子批进行调度,生成新的调度路线Rnew。 (7)Cnew表示新调度路线的最长完工时间,Copt表示最优调度路线的最长完工时间,判断Cnew≤Copt,若成立,则令Ropt=Rnew,转步骤(3);否则,最优路线不变,直接转步骤(3)。 图7描述的是工件B的加工顺序树,其加工数量设定为10。 图7 工件B加工顺序树 图8为工件B的整批调度甘特图,最后一道工序OB6为关键路径工序,工序OB6开始加工时间为200min,记为psB6,然后向前查找关键工序,由于工序OB4的加工完成时间为200min,与psB6相等,所以工序OB4为关键路径工序,以此类推,从调度方案最后向前查找得到的关键路径为OB2→OB4→OB6,因此关键路径工序子批集σkey为{OB2,OB4,OB6}。使σkey内所有工序的批次数加1,调整加工顺序树,如图9所示,其中工序OB2、OB4、OB6的批次数量为2。对已调整的加工顺序树中所有工序批次进行重新调度,得到工艺路线如图10所示。 图8 工件B整批调度甘特图 图9 第一次调整后顺序加工树 图10 新调度甘特图 更新关键路径工序子批集σkey为{OB2-1,OB4-1,OB5,OB6-2},对新的关键路径工序进行再分批,直到分批量达到给定最小值,分批结束,得到加工时间相对最短的工序分批方案和加工工艺路线。 3.3 基于关键路径工序分批调度算法 综上所述,算法流程步骤如下。 (1)输入产品的工艺信息,即工件工序集σfull以及各个工序之间的顺序约束关系,工序加工设备集σM等。 (2)将工件工序输入到调度模块,利用机器短用时策略调度所有工序。①由于工件工序间有顺序约束,首先要确定可加工工序子批集σjob,开始时刻所有机器为空闲。②利用短用时策略和长路径策略确定当前空闲机器加工工序。③更新可加工工序子批数量,将已加工的工序子批数量减1。机器选择可加工工序加工,更新可加工工序子批集σjob,如果工序子批批次数量大于1,根据可加工工序子批集确定算法动态更新可加工工序子批集σjob。④判断σjob=∅是否成立,若成立,本次调度结束,返回调度路线Ropt,转到步骤(3);否则转到步骤②。 (3)判断是否所有工序批次均为1,若是,则判定当前调度为整批调度,Rnew=Ropt=Rcur,转到步骤(5);否则Rnew=Rcur,转到步骤(4)。 (4)判断Tnew≤Topt若成立,则Ropt=Rnew,转到步骤(5);否则,直接转到步骤(5)。 (5)确定Rnew的关键路径以及关键路径工序子批集σkey。 (6)使子批集σkey里的工序批次数加1,即lσ←lσ+1,非关键路径工序子批数量不变。 (7)判断关键路径工序子批集中最大的分批数与给定的最大分批批次的大小:若maxlσ≤llimit,则转到步骤(2);否则,转到步骤(8)。 (8)返回最优调度路线Ropt。 (9)输出加工工艺路线和分批方案。 本节通过实际加工案例进行实验分析,验证本文算法的可行性和有效性。算法运行环境配置为Inteli7CPU,3.4GHz主频,8G内存,Windows7操作系统,其中基于遗传算法的调度排序交叉概率设定为0.85,变异概率为0.2,进行多次仿真实验。 线束工艺产品车间,拟加工A和B两个线束零部件(以下简称工件A、工件B),加工图纸见图11,加工数量均为100,共有4台加工设备。加工工序顺序如图12所示,加工工件工序加工时间见表1,抽象出虚拟加工顺序树如图13所示。设定分批加工的最小批量为20,加工准备时间设定为单工件工序在各机器上的加工时间,通过以上算法对工件工序加工顺序进行调度安排。 (a)工件A (b)工件B图11 线束零部件图纸 (a)工件A (b)工件B图12 工序约束图 在加工开始时刻,可加工工序为叶子节点工序,根据图12加工顺序树,开始时刻可加工工序子批集σjob为{OA1,OA2,OB1,OB2}。开始时刻每个设备均为空闲状态,所以根据机器选择策略选择合适的工序加工。如工序OB1和OB2在M1上的 表1 工件工序加工时间表 (a)工件A (b)工件B图13 虚拟加工顺序树 需求时间相等,所以根据长路径策略,OB1和OB2的最短路径长度分别为25和10,所以机器M1选择工序OB1加工。当工序OB1加工完毕,触发工序OB3变成可加工工序,那么当前可加工工序子批集σjob为{OB2,OB3},由于工序OB2在机器M1上加工时间少于OB3在机器M1上加工时间,所以选择工序OB2。根据上述步骤更新可加工工序子批集并确定加工机器,直至可加工工序子批集为空,生成调度方案如图14所示。 图14 整批加工调度甘特图 由图14可以看出,整批加工的最长完工时间长达3015min,并且机器利用率极低。整批加工后的关键路径工序为OA1→OB3→OB4,对该路径所有工序批次数量加1。图14中黑色区域表示加工准备时间。 工件工序分批加工后,最小批量不能小于20,即最大批次不能大于5。每次分批后,对关键路径和调度方案进行审查,若批量小于给定最小值,则分批结束。表2给出了基于关键路径工序每次分批的结果,其中分批方案为各道工序的批 表2 基于工序分批结果 次数,用{lA1,lA2,lA3,lB1,lB2,lB3,lB4}表示。通过分析多目标值最长完工时间和总批次数可知,第五次分批为最优分批,分批方案为{3,2,2,2,1,4,4},总批次数量为18,最长完工时间为1870min,机器利用率达到95.79%,图15为该次分批后调度甘特图。而继续分批得到的第6次、第7次调度结果的总批次数和最长完工时间相对第五次均有所增加,且机器利用率也降低至91.5%左右。 图15 基于工序最优(第五次)分批调度甘特图 为了验证本模型实验结果的真实性和有效性,将本模型与传统的基于工件分批调度模型[11]进行对比,这里以基于遗传算法的分批调度模型为参照。表3为遗传算法迭代100次的分批结果。其中,当lA/lB为1/2、1/3等分批次数时,最长完工时间与lA/lB为1/1分批的最长完工时间相同,故不再赘述,只列出最长完工时间变动的分批方案,在批量不小于20的要求下,最优分批方案为{4,4,4,5,5,5,5},总分批数量为32,最长完工时间为1900min,机器利用率达到92.11%,图16为该分批方案调度甘特图。 表3 基于遗传算法分批结果 图16 基于遗传算法工件分批的最优调度甘特图 根据表4,基于关键路径工序的分批调度算法在保证最长完成时间相对优化的情况下,为每个工序安排其合适的批次数,使总加工批次由32降为18,减少了42%,机器利用率由92.1%提高到95.8%。 表4 调度方案对比表 (1)根据工序间的不同特点,提出基于工序进行不等量分批概念,为每道工序安排其合适的批量大小。 (2)采用动态更新可加工工序子批集与机器选择的方法,及时调整加工路线。 (3)以关键路径工序为中心进行分批,并在调度过程中考虑加工准备时间,增加工艺柔性和实用性。本文从总加工批次和最长完工时间两方面与基于工件分批的调度方案进行比较,用实验结果验证了基于工序分批调度的可行性和有效性。 (4)本文重点讨论对工序进行分批,建模过程中采用了对关键路径工序进行分批的调度方法,该解决方法相对简单易用,比较适合加工装配型车间的生产,但具有陷入局部最优的可能。为了提高算法的全局搜索能力,同时适应更加复杂的作业车间生产,今后将考虑采用禁忌搜索、粒子群算法以及混合算法等方法进一步对模型进行优化和改进。 [1] 王万良, 吴启迪, 宋毅. 求解作业车间调度问题的自然改进自适应遗传算法 [J]. 系统工程理论与实践, 2004, 2(2):58-62.WangWanliang,WuQidi,SongYi.ModifiedAdaptiveGeneticAlgorithmsforSolvingJob-shopSchedulingProblems[J].SystemsEngineering—Theory&Practice, 2004, 24(2):58-62. [2]HuangRH.Multi-objectiveJob-shopSchedulingwithLotSplittingProduction[J].InternationalJournalofProductionEconomics, 2010, 124(1):206-213. [3] 刘晓平, 徐本柱, 彭军, 等. 工件工序可并行的作业车间调度模型与求解 [J]. 计算机辅助设计与图形学学报, 2012, 24(1):120-127.LiuXiaoping,XuBenzhu,PengJun,etal.ModelandSolutionofJob-shopSchedulingforParallelProcesses[J].JournalofComputer-AidedDesign&ComputerGraphics, 2012, 24(1):120-127. [4] 王海燕. 基于混合差分进化算法的制造过程分批优化调度研究[D]. 杭州:浙江工业大学, 2011. [5] 宋代力, 张洁. 蚁群算法求解混合流水车间分批调度问题 [J]. 计算机集成制造系统, 2013,19(7):1640-1647.SongDaili,ZhangJie.BatchSchedulingProblemofHybridFlowShopBasedonAntColonyAlgorithm[J].ComputerIntegratedManufacturingSystems, 2013,19(7):1640-1647. [6] 陆汉东, 何卫平, 周旭, 等. 基于禁忌搜索的柔性作业车间分批调度 [J]. 上海交通大学学报, 2012, 46(12):2003-2008.LuHandong,HeWeiping,ZhouXu,etal.AnIntegratedTabuSearchAlgorithmfortheLotStreamingProbleminFlexibleJobShops[J].JournalofShanghaiJiaotongUniversity, 2012, 46(12):2003-2008. [7]LowCY,HsuCM,HuangKI.BenefitsofLot-splittinginJob-shopScheduling[J].InternationalJournalofAdvancedManufacturingTechnology, 2004, 24(9/10):773-780. [8] 潘多科, 朱剑英. 多工艺路线的批量生产调度优化[J]. 机械工程学报, 2004, 40(4):36-39.PanDuoke,ZhuJianying.OptimizationMethodforaJob-shopSchedulingProblemwithAlternativeMachinesintheBatchProcess[J].ChineseJournalofMechanicalEngineering, 2004, 40(4):36-39. [9]JeongHI,ParkJW,LeachmanRC.ABatchSplittingMethodforaJobShopSchedulingProbleminanMRPEnvironment[J].InternationalJournalofProductionResearch, 1999, 37(15):3583-3598. [10] 孙志峻, 安进, 黄卫清. 作业车间多工艺路线批量作业计划优化[J].中国机械工程, 2008, 19(2):183-187.SunZhijun,AnJin,HuangWeiqing.LotSchedulingwithMultipleProcessRoutesinJobShop[J].ChinaMechanicalEngineering, 2008, 19(2):183-187. [11]ChanLY.TheApplicationofGeneticAlgorithmstoLotStreaminginaJobSchedulingProblem[J].InternationalJournalofProductionResearch, 2009, 47(12):3387-3412. [12] 陈伟达,达庆利. 工艺路线可变车间作业调度的两级遗传算发[J].系统工程学报,2002,17(2):161-166.ChenWeida,DaQingli.Job-shopSchedulingwithAlterableCraftBasedonBilevelGeneticAlgorithms[J].JournalofSystemsEngineering, 2002, 17(2):161-166. [13] 陶俐言, 聂倩, 王志峰, 等. 面向变批量生产的制造单元构建方法[J]. 计算机集成制造系统, 2014, 30(10):2411-2418.TaoLiyan,NieQian,WangZhifeng,etal.FormationTechnologyofManufacturingCellDesignforScalableBatchProduction[J].ComputerIntegratedManufacturingSystems, 2014, 30(10):2411-2418. [14] 陈亚绒, 周余庆, 周宏明, 等. 两阶段求解的可重构虚拟制造单元构建方法[J]. 中国机械工程, 2013, 24(22):3024-3029.ChenYarong,ZhouYuqing,ZhouHongming,etal.VirtualManufacturingCellFormationMethodforReconfigurableManufacturingBasedonTwo-stageSolving[J].ChinaMechanicalEngineering, 2013, 24(22):3024-3029. [15]XieZ,HaoS,YeG,etal.ANewAlgorithmforComplexProductFlexibleSchedulingwithConstraintbetweenJobs[J].Computers&IndustrialEngineering, 2009, 57(3):766-772. [16] 谢志强, 杨静, 杨光, 等. 可动态生成具有优先级工序集的动态Job-Shop调度算法 [J]. 计算机学报, 2008, 31(3):502-507.XieZhiqiang,YangJing,YangGuang,etal.DynamicJob-shopSchedulingAlgorithmwithDynamicSetofOperationHavingPriority[J].ChineseJournalofComputers, 2008, 31(3):502-507. [17] 谢志强, 辛宇, 杨静. 基于设备空闲事件驱动的综合调度算法[J]. 机械工程学报, 2011, 47(11):139-147.XieZhiqiang,XinYu,YangJing.IntegratedSchedulingAlgorithmBasedonEvent-drivenbyMachines’Idle[J].JournalofMechanicalEngineering, 2011, 47(11):139-147. [18] 周驰, 高亮, 高海兵. 基于PSO的置换流水车间调度算法[J]. 电子学报, 2006, 34(11):2008-2011.ZhouChi,GaoLiang,GaoHaibing.ParticleSwarmOptimizationBasedAlgorithmforPermutationFlowShopScheduling[J].ActaElectronicaSinica, 2006, 34(11):2008-2011. [19] 苏子林. 车间调度问题及其进化算法分析[J].机械工程学报, 2008, 44(8):242-247.SuZilin.Job-shopSchedulingProblemandItsEvolutionAlgorithmAnalysis[J].ChineseJournalofMechanicalEngineering, 2008, 44(8):242-247. (编辑 王旻玥) ProblemsandSolutionsofFlexibleJob-shopSchedulingwithOperationLot-splitting XuBenzhuJiJingFeiXiaolu HefeiUniversityofTechnology,Hefei,230009 Consideringthateachoperationinflexiblejob-shopschedulingwithlot-splittinghaditsownappropriatelot-size,theconceptofschedulingwithlot-splittingwasproposedbasedonoperations,andaschedulingmodelwithlot-splittingwasestablishedbasedoncriticalpathoperations.Thismodelcoulddynamicallyupdatemachinablesub-lotset,updateavailablemachines,determineoptimalprocessingroutesandappropriateoperationlot-sizesthusmakespanmightbeoptimizedandtotallotquantitymightbereduced.Theexperimentalresultsshowthat,comparedwithlot-splittingbasedonworkpieces,usingtheestablishedschedulingmodelthemakespanmaybeoptimized,machineutilizationmaybeimproved,totalmachinedlotquantitymaybereduced(42%)andschedulingmanagementcomplexitymaybedecreased. flexiblejobshop;schedulingmodelwithlot-splitting;operationlot-splitting;non-equalsizelot-splitting 2016-01-25 国家自然科学基金资助项目(61300118);安徽省自然科学基金资助项目(1308085MF102);安徽省科技攻关项目(1401B042009);中央高校基本科研业务费专项资金资助项目(2014HGCH0014) TP391.7 10.3969/j.issn.1004-132X.2016.23.016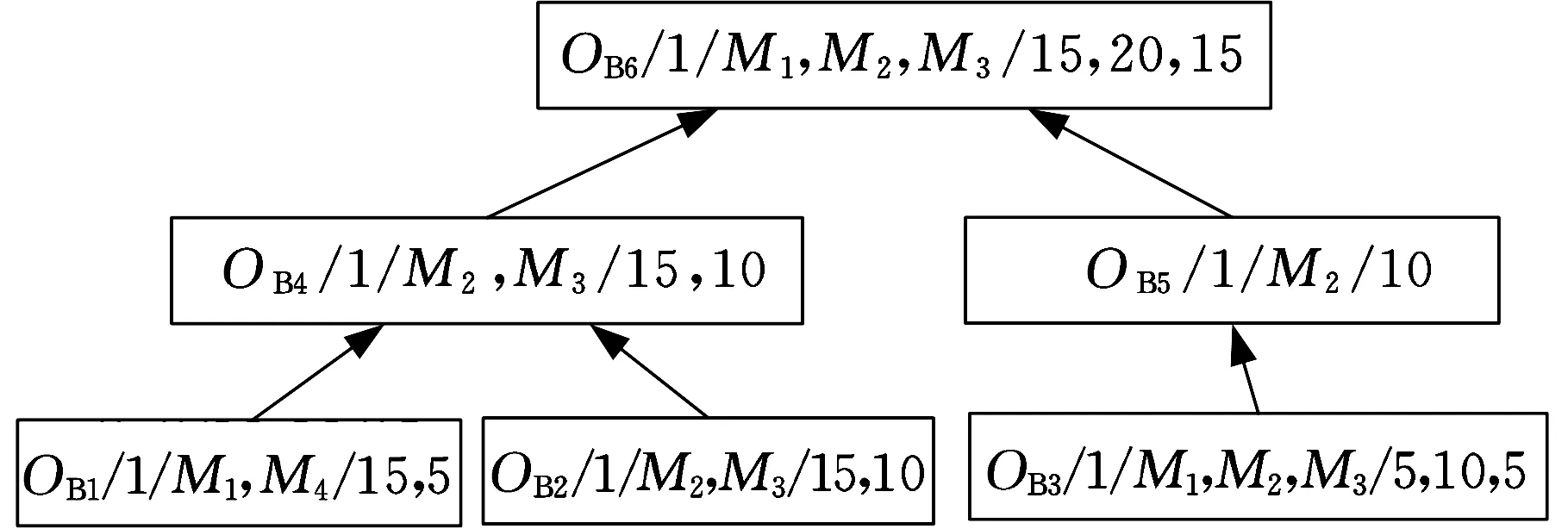

4 实例分析

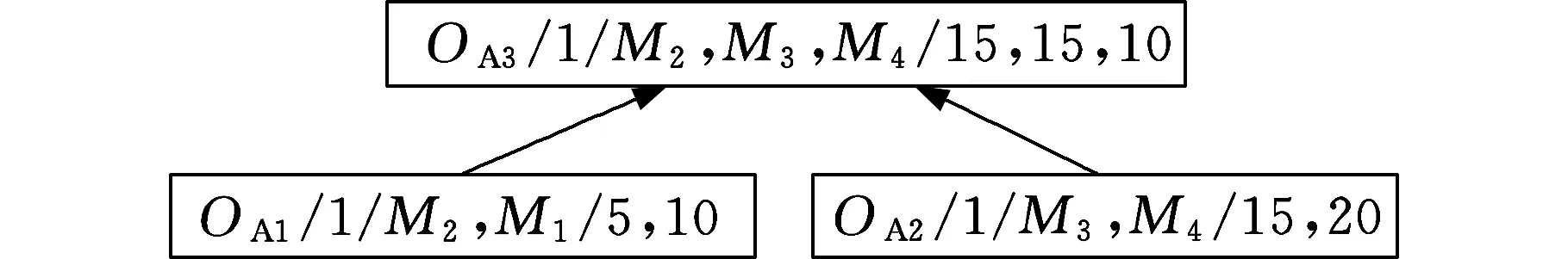


5 结论

