基于小波神经网络的高精度惯导重力扰动补偿方法

周 潇，杨功流，蔡庆中

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191）

基于小波神经网络的高精度惯导重力扰动补偿方法

周 潇，杨功流，蔡庆中

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191）

重力扰动矢量(空间同一点实际重力与正常重力之差，包括垂线偏差和重力异常两部分) 一直是惯性导航系统的重要误差源之一。针对重力扰动误差精确补偿问题，推导并建立了考虑重力扰动的惯导误差方程，并提出了基于小波神经网络的重力扰动补偿方法。通过仿真验证了小波神经网络的重力扰动补偿方法对惯导导航精度的提高效果。24 h仿真结果表明：所提出的重力扰动补偿方法能有效减小惯导导航系统误差，经重力扰动矢量补偿后，速度误差最大能减小约0.2 m/s，降低约30%，位置误差最大能减小约3000 m，降低约25%。

捷联惯导系统；重力扰动补偿；惯导误差方程；小波神经网络

惯性导航系统[1]不需要任何外来信息，也不会向外辐射任何信息，仅靠惯性导航系统本身就能在全天侯条件下，在全球范围内和任何介质环境里自主地、隐蔽地进行连续的三维定位和三维定向，具有诸多其他导航系统无法比拟的优点，故广泛应用于军事，民用等诸多领域。随着惯性器件精度的逐步提高以及高精度捷联惯性导航系统应用需求的提出，重力扰动已经成为高精度捷联惯性导航系统最主要的剩余误差源之一[2-3]。

为了解决这一问题，本文提出了一种基于小波神经网络的重力扰动预测及补偿方法，并通过仿真试验验证了该方法对重力扰动的预测精度以及在高精度惯导中的补偿效果。

1 考虑重力扰动的惯导误差方程

1.1 惯导系统原理图及坐标系定义

在惯性导航系统中，陀螺仪和加速度计通过稳定平台安装在载体上，分别测量载体相对惯性空间的角运动信息和线运动信息，在给定相关初值和其他必要信息（如重力信息）的情况下，经过一系列运算和控制可以得到载体相对于导航坐标系的位置、速度和姿态等信息。图1为本文所提出的考虑重力扰动补偿的惯导系统原理图[4]。

图1 惯性导航系统原理图Fig.1 Principle of inertial navigation system

坐标系定义：b系—载体坐标系；n系—导航坐标系（在本文中取为东-北-天当地水平指北坐标系）；e系—地固坐标系；i系—惯性坐标系。

1.2 重力扰动的基本定义

重力扰动矢量δg为实际重力矢量与正常重力矢量γ之间的差值[5]：

式中：0γ可以根据正常重力模型得到，通常采用1980年国际正常重力公式：

式(3)中：g0=9.780327，a=0.0053024，b=0.0000058。重力扰动矢量可以表示为

式(4)中：η和ξ分别为东西向和南北向垂线偏差，一般在10″左右，个别地区可以达到30″；ΔgE、ΔgN、分别为重力扰动矢量的东向、北向、垂向分量。

1.3 考虑重力扰动的捷联惯导误差方程推导及分析

捷联惯性导航误差方程[6-8]：

姿态误差方程为

式(5)中：

式(6)中：δKG为陀螺标度系数误差；δG为陀螺安装误差矩阵；φ为姿态角误差；为坐标系转换矩阵；为载体系下的陀螺输出；nε为导航坐标系下的陀螺漂移；为指令角速度误差，且可表示为

式中：L为载体所在位置的纬度；RM、RN、h分别为载体所在位置的子午圈半径、卯酉圈半径和海拔高度。

根据公式(5)可知，引起惯导姿态误差的主要误差源有陀螺的输出误差，除此之外还可以通过速度位置的耦合关系引起姿态误差，体现于一项。

速度更新误差方程为

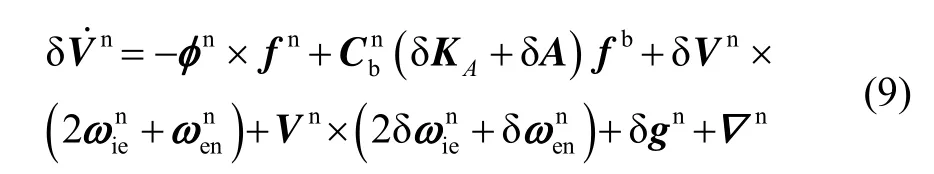
式(9)中：

式中：δKA为加速度计标度系数误差；δA为加速度计安装误差矩阵；fn为导航坐标系下的加速度计输出；为导航坐标系下加速度计零偏；δgn为导航坐标系下的重力扰动。

位置更新误差方程为

式中：L、λ分别为地理纬度和经度。

由公式(9)可知，引起惯导系统速度误差的误差源主要有加速度计输出误差惯导前一时刻积累的速度误差在导航坐标系下的投影、速度位置的耦合误差项以及重力扰动δgn。

由公式(11)可知，引起惯导系统位置误差的主要误差源为惯导前一时刻的速度误差δVn以及速度位置的耦合误差。

通过以上对重力扰动在惯导系统中的误差分析可以得出，重力扰动 δgn首先通过公式(9)引起惯导的速度误差，速度误差进一步通过公式(11)引起惯导系统位置误差，最终通过公式(5)引起惯导的姿态误差，并且惯导误差随时间的增长而发散。

在以往的惯导系统中，重力扰动所引起的误差远远小于由惯性器件所带来的误差，所以在惯导解算时通常对重力扰动所带来的系统误差予以忽略。但是随着惯性器件以及惯导标定技术的快速发展，重力扰动已成为惯导解算中影响系统误差的主要来源，制约着惯导导航精度的进一步提高，所以必须对惯导解算中的重力扰动项进行补偿。

2 重力扰动数据小波神经网络的预测方法

小波神经网络（Wavelet Neural Network，WNN）是将小波分析理论和神经网络相结合的一种神经网络模型，可以实现时域和频域的同时分析，具有良好的局部特性，较强的学习能力和任意函数逼近能力[8-9]。WNN以传统的BP神经网络构架为支架，将神经网络隐含层的传输函数用小波函数来替代，实现信号的前向传播和误差的方向传播。本文以3层神经网络为例，设计出基于局部区域重力扰动数据的小波神经网络预测模型，其网络结构如图2所示。

图2 小波神经网络结构图Fig.2 Structure of wavelet neural network

图2中：X1,X2, …,Xk为小波神经网络的输入参数，本文选载体所在位置的经纬度(λ,L)作为输入参数；Y1,Y2,…,Yk为小波神经网络的预测值输出，这里为重力扰动的水平分量，东西向和南北向的垂线偏差η、ξ和垂向重力扰动Δg。ωij和ωjk为小波神经网络权值。在输入信号为xi(i=1,2, …,k)时，隐含层输出公式为[10-11]

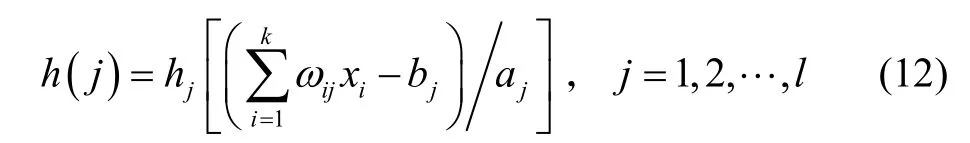
式中：h(j)为隐含层第j个节点输出值；ωij为输入层和隐含层之间的连接权值；bj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子；hj为小波基函数。小波神经网络输出层的输出公式为

式中：ωik为隐含层到输出层的连接权值；h(i)为第i个隐含层节点的输出；l为隐含层节点数；m为输出层节点数。

在小波神经网络的应用中，小波基函数的选择对于网络预测效果影响非常的大，根据不同的问题选择不同的基函数，但是目前尚没有理论上的支撑。Morlet小波函数多用于分类、图像识别和特征提取；高斯一阶导数多用于函数估计和预测；Mexican hat 小波函数多用于系统辨识等。本文通过反复计算得出，当选择高斯一阶导数作为小波基函数时，网络模型有着较高的预测精度。

小波神经网络权值参数修正算法类似于BP神经网络权值得修正，采用梯度修正法修正网络权值和小波基函数参数，从而使小波神经网络预测输出不断地逼近期望输出[12]。

计算网络预测误差：

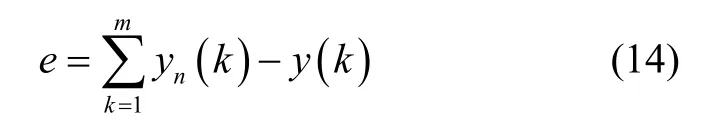
式中：yn(k)为期望误差；y(k)为小波神经网络预测输出。

根据预测误差e修正小波神经网络的权值和小波基函数系数：

式中：η为小波神经网络学习速率，取值在0到1之间。

本文提出的重力扰动数据小波神经网络学习算法的步骤如图3所示。

图3 小波神经网络算法流程图Fig.3 Flow chart of wavelet neural network

1）网络初始化。随机初始化小波函数伸缩因子aj,平移因子bj以及网络连接权值ωij、ωik，并设置网络学习速率η。

2）样本分类。将样本分为训练样本和测试样本。

3）预测输入。将训练样本输入网络，计算网络输出和网络预测误差e。

4）权值修正。根据网络预测误差e对网络权值和小波函数参数进行修正，使网络预测值逼近期望值。

5）判断e值。判断网络预测误差e是否满足给定误差阈值，若满足则结束训练，否则返回步骤3）重新训练。

3 仿真分析

3.1 重力扰动建模仿真

仿真条件：仿真模拟数据来自美国国家大地数据测量局提供的太平洋某片海域N40～43°、W160°～163°的重力扰动格网数据，格网数据的空间分辨率为1′×1′。网格内重力扰动数据的分布图如图4所示。

采用小波神经网络建立重力扰动预测模型时，将格网区域内的重力扰动数据分成两个部分：一部分为训练样本，占总点数的70%；另一部分为测试样本，占总点数的30%。本文随机选取10个点对小波神经网络模型的预测精度进行评价，并与反距离加权（IDW）插值结果相比较，计算结果如表1、表2所示。

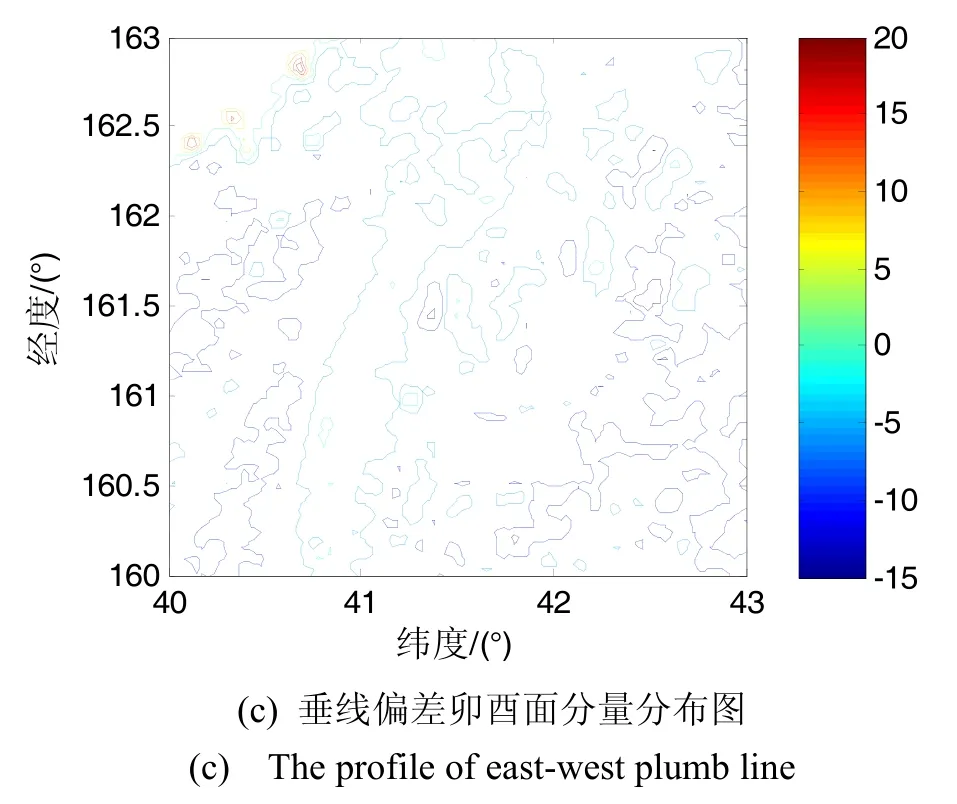
图4 格网区域内重力扰动分布图Fig.4 Profile of gravity disturbance in the selected mesh region

由表1和表2的对比结果可以看出，利用小波神经网络对格网区域内重力扰动数据的预测精度明显高于采用IDW插值方法的预测精度。当采用小波神经网络进行预测时，重力扰动各分量与真实值接近，求差后重力异常误差的极值仅在1 mGal左右，垂线偏差误差的极值也都在5″之内，从而说明小波神经网络对格网内的重力扰动数据有很好的预测效果，预测精度完全可以满足高精度惯导对于重力扰动精度的需求。

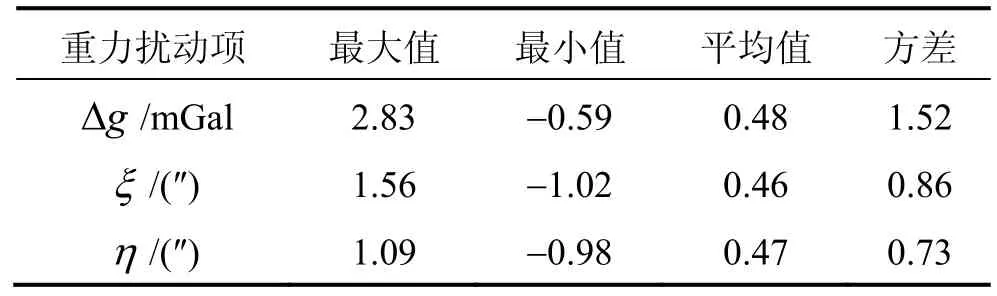
表1 IDW插值误差评价表Tab.1 Performance of IDW interpolation

表2 小波神经网络预测误差评价表Tab.2 Performance of WNN estimation

3.2 重力扰动对惯导补偿仿真

仿真条件：三个陀螺的常值漂移为3×10-3(°)/h，随机游走系数为2×10-4/h，加速度计的零漂均为10×10-6g。为了更好地分析重力扰动对惯导误差的影响，故忽略其他误差的影响，设安装误差角为零，无初始对准误差。仿真过程中忽略高度通道的影响。仿真步长设为1 s，仿真时间为24 h。模拟舰船实验，故设载体的东向、北向速度为5 m/s，天向速度为0 m/s。仿真中利用提供的1′×1′的重力格网数据插值后得到网格区域内的重力扰动数据来模拟实际重力扰动，加入到惯导系统中可以得到无重力扰动补偿时捷联惯导误差，仿真结果如图5所示。采用本文提出的小波神经网络重力扰动补偿方法，进行重力扰动补偿后，得到的系统误差如图6所示。

图5 无重力扰动补偿惯导系统误差Fig.5 System errors of INS without gravity disturbance compensation

由图5、图6的仿真结果可以得出：经过小波神经网络重力扰动补偿后的惯导速度误差和位置误差都有明显减小。补偿后的速度误差最大能减小约0.2 m/s，降低约30%，位置误差最大能减小约3000 m，降低约25%。以上分析表明，本文提出的重力扰动补偿方法可以有效地提高高精度惯导的导航精度。

图6 重力扰动补偿后惯导系统误差Fig.6 System errors of INS with gravity disturbance compensation

4 结 论

随着惯性元件精度的不断提高以及惯导技术的快速发展，重力扰动已成为惯性导航系统的重要误差源，必须对其进行补偿才能进一步的提高惯导的导航精度。本文建立了考虑重力扰动矢量的惯导系统误差方程，并提出了基于小波神经网络的重力扰动补偿方法。通过仿真验证了小波神经网络的重力扰动补偿方法对惯导导航精度的提高效果。仿真结果表明：本文所提出的重力扰动补偿方法能有效地减小惯导导航系统误差；经重力扰动矢量补偿后，仿真24h速度误差最大能减小约0.2 m/s，降低约30%，位置误差最大能减小约3000 m，降低约25%。

（References）：

[1]吴太旗, 欧阳永忠, 陆秀平, 等. 重力匹配导航的影响模式分析[J]. 中国惯性技术学报, 2011, 19(5)：559-564.Wu Tai-qi, Ouyang Yong-zhong, Lu Xiu-ping, et al. Analysis on effecting mode of several essential factors to gravity aided navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(5): 559-564.

[2] 周潇, 杨功流, 王晶, 等. 基于Kalman滤波原理对惯导中重力扰动的估计及补偿方法[J]. 中国惯性技术学报,2015, 23(6): 721-726.Zhou Xiao, Yang Gong-liu, Wang Jing, et al. Estimation and compensation for gravity disturbance based on Kalman filtering in inertial navigation[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 721-726.

[3]Man X, Fang J CH, Ning X L. An overview of autonomous navigation for a gravity-assist interplanetary spacecraft[J]. Progress in Aerospace Sciences, 2013, 63: 56-66.

[4]Rummel R, Yi W, Stummer C. GOCE gravitational gradiometry[J]. Journal of Geodesy, 2011, 85: 777-790.

[5]Cai Shao-kun, Zhang Kai-dong, Wu Mei-ping. Improving airborne strapdown vector gravimetry using stabilized horizontal components[J]. Journal of Applied Geophysics.2013: 79-89.

[6]Li X. Strapdown INS/DGPS airborne gravimetry tests in the Gulf of Mexico[J]. Journal of Geodesy, 2011, 85:597-605.

[7] 王虎彪, 王勇, 方剑. “最小均方差旋转拟合法”重力辅助导航仿真研究[J]. 中国科学: 地球科学, 2012, 42(7):1055-1062.Wang Hu-biao, Wang Yong, Fang Jian. Simulation research on a minimum root-mean-square error rotationfitting algorithm for gravity matching navigation[J].Science China: Earth Sciences, 2012, 42(7): 1055-1062.

[8]战德军, 戴东凯, 张忠华, 等. 单轴旋转INS/GPS组合导航中重力垂线偏差引起的姿态误差分析[J]. 中国惯性技术学报, 2014, 22(3): 301-305.Zhan De-jun, Dai Dong-kai, Zhang Zhong-hua et al.Analysis of gravity vertical deflection-induced attitude error in single-axis rotation INS/GPS integrated navigation system[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 301-305.

[9]Falamarzi Y, Palizdan N, Huang Y F, et al. Estimating evapotranspiration from temperature and wind speed data using artificial and wavelet neural networks (WNNs)[J].Agric. Water Manag., 2014, 140: 26-36.

[10]赵忠, 王鹏. 高精度惯性导航系统垂线偏差影响与补偿[J]. 中国惯性技术学报, 2013, 21(6): 701-705.Zhao Zhong, Wang Peng. Analysis and compensation of vertical deflection effect on high accuracy inertial navigation system[J]. Journal of Chinese Inertial Technology,2013, 21(6): 701-705.

[11]Alexandridis A K, Zapranis A D. Wavelet neural networks:a practical guide[J]. Neural Networks, 2013, 42: 1-27.

[12]Guan C, Luh P B, Michel L D, et al. Very short-term load forecasting: wavelet neural networks with data pre-filtering[J]. IEEE Transactions on Power Systems, 2013,28(1): 30-41.

Compensation on gravity disturbance for high-precision INS based on wavelet neural network

ZHOU Xiao, YANG Gong-liu, CAI Qing-zhong
(1. School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China;2. Science and Technology on Inertial Laboratory, Beijing 100191, China)

The gravity disturbance is one of the important error sources of inertial navigation system, which is the difference between the actual gravity and normal gravity on the same point, and is composed of two parts: deviation of plumb line and gravity anomaly. In this paper, the error equation of inertial navigation system considering gravity disturbance is derived and established, and the gravity disturbance compensation based on wavelet neural network is proposed. The 24 h simulation results show that the proposed gravity disturbance compensation method can effectively reduce the navigation errors of INS, and after the gravity disturbance compensation, the maximum velocity error and the maximum position error are reduced by about 0.2 m/s and 3000 m respectively, therefore the velocity accuracy and the position accuracy can be improved by about 30% and 25%, respectively.

strapdown inertial navigation system; gravity disturbance compensation; inertial navigation error equation; wavelet neural network

U666.1

A

1005-6734(2016)05-0571-06

10.13695/j.cnki.12-1222/o3.2016.05.003

2016-06-03；

2016-09-12

国家自然科学基金（61340044，11202010）

周潇（1987—），男，博士研究生，从事惯性技术研究。E-mail: buaa17zhou@163.com

联 系 人：杨功流（1967—），男，教授，博士生导师。E-mail: bhu17-yang@139.com