基于D-最优的惯性平台自标定方案设计

王 琪，汪立新，沈 强，秦伟伟

（火箭军工程大学，西安 710025）

基于D-最优的惯性平台自标定方案设计

王 琪，汪立新，沈 强，秦伟伟

（火箭军工程大学，西安 710025）

惯性平台自标定的标定方案设计目前多是依靠经验人为设计，而没有比较系统的标定方案设计方法，为解决此问题，提出了一种基于D-最优理论的惯性平台自标定方案设计方法。首先分析给出了包含36个待估计参数的平台系统误差模型；然后以陀螺仪和加速度计的输出模型为回归模型，将惯性平台自标定看作一个广义的多元回归问题，以D-最优理论为优化准则，提出了并行设计和串行设计两种标定方案设计思路。将得到的优化方案与传统的十六位置标定方案进行了仿真对比分析，仿真结果表明：优化方案的陀螺仪误差系数、加速度计误差系数和加速度计安装误差系数标定相对误差都在1%以下，与传统十六位置标定方案的标定精度相当；但优化方案的陀螺仪安装误差标定相对误差在 5%左右，远远优于传统十六位置标定方案 25%的相对误差；而且优化方案的标定位置更少，能够减少标定时间，验证了标定方案设计思路的正确性。

D-最优；惯性平台；自标定；误差模型；最优位置

制导工具误差和方法误差是影响制导武器命中精度的主要因素，前者占主要成份，而惯性仪表的精度在很大程度上决定了惯性平台系统的使用精度，因此在使用时必须进行补偿。对于高精度惯性平台，对误差进行标定并进行补偿就显得更为重要[1]。目前对于惯性平台的误差标定和补偿，主要方法是在地球重力场内的多位置翻滚自标定方法，将地球重力加速度和自转角速度作为加速度计和陀螺仪的输入，得到加速度计和陀螺仪的输出，利用最小二乘法估计出平台的误差系数。在这个过程中，标定位置的选择将影响加速度计和陀螺仪的输入大小，从而直接影响误差标定的精度[2]。因此标定位置的选择，即标定方案的设计对于提高惯性平台自标定精度、减少标定时间有着重要作用。但是目前对于标定方案的设计，大多是依靠人为经验进行设计，并没有比较系统的标定方案设计方法，而惯性平台自标定实质上是一个广义的多元回归问题，因此可以利用D-最优理论对标定方案进行设计[3]。

本文首先给出了惯性平台中的坐标系转换关系和加速度计、陀螺仪的误差模型，然后将加速度计和陀螺仪的误差模型看作广义多元回归模型，利用 D-最优理论进行标定方案设计。针对惯性平台自标定中需要同时考虑加速度计和陀螺仪的输出响应的问题，给出了两种标定方案设计思路，并分别得到了两个标定方案。最后将得到的标定方案与传统的十六位置标定方案进行了仿真对比分析，验证了标定方案设计思路的正确性。

1 平台误差模型

1.1 坐标系定义及转换矩阵

首先给出平台中的坐标系定义，假设平台由三个单自由度积分陀螺仪与三个摆式加速度计组成，如图1所示。

图1 平台组成图Fig.1 Platform geometry

设陀螺仪i轴绕其o、s轴的安装误差为Δoi、Δsi，加速度计i轴绕其 p、o轴的安装误差为θpi、θoi，则平台坐标系p到X陀螺仪和X加速度计坐标系的转换矩阵分别为[4]

在惯性平台自标定试验中，如果平台先绕外环轴转动角度γ，再绕台体轴转动角度α，则从地理坐标系n（东北天坐标系）到平台坐标系p的转换矩阵为

1.2 陀螺仪和加速度计误差模型

陀螺仪的静态误差模型为[5]

加速度计的静态误差模型为[4]

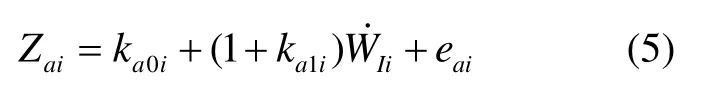
结合上文中的坐标系转换矩阵，将式(1)～(3)代入式(4)和(5)，可得陀螺仪和加速度计的输出模型分别为(以X陀螺仪和X加速度计为例）

因此，我们可将式(6)看作5维因素空间中的有8个待估计参数的广义回归模型，将式(7)看作3维因素空间中的有4个待估计参数的广义回归模型，以回归试验优化的方法进行标定方案设计。

2 D-最优理论

最优试验设计是基于回归模型的一类试验设计方法，又称回归设计[7]。对于广义回归模型：

式中：tε为服从分布的相互独立的随机变量；为因素空间X中的一点，若因素空间为p维欧式空间，则xt就是p维向量 (是因素空间X中的小于或等于p元的连续函数；为m个待估计参数。

假设试验方案ε由N个试验点x1,x2,… ,xN组成，那么广义回归模型(8)的结构矩阵为[8]

其信息矩阵为

D-最优理论认为，在同一模型(8)下，对两个不同的试验方案1ε和2ε，如果有，则在D-优良性下方案1ε比2ε好[9]。本文将会依据该准则设计基于D-最优的惯性平台自标定方案。

3 自标定方案设计

在惯性平台自标定中，由于标定的误差系数较多，如果采用构造 D-最优设计的数值方法来进行方案设计，会产生计算量大、回归方程最优解不易求得等问题[10]。根据以往的经验可知，相邻位置的α和γ之间一般间隔相同的角度（一般为45°或90°），因此可以采取一种遍历寻优的方法，只需要确定初始位置α1、γ1和相邻位置的间隔角度Δα、Δγ，以D-最优理论为设计准则，就可以通过遍历搜索的方式得到最优方案。

首先给出α和γ角的变化规律如表1所示。接下来就可以以表1所示的α和γ角的变化规律为基础，以陀螺仪和加速度计的输出模型为回归方程进行最优标定方案设计。

表1 α和γ角变化规律Tab.1 Changing characteristics ofαandγ

遍历寻优的算法流程如下：

1）设置1α和1γ的步长，本文选择相等的步长5°，且1,1[0,180]α λ∈ 。

2）设置Δα和Δγ的值，依次取Δα=45°、90°，

3）设置标定位置数N∈[m, 16]，其中m为待估计参数个数。

4）求取每一个标定位置数N下的最优标定方案。对于每一个Δα和Δγ的值，按照表1所示的变化规律，计算出180/5=36组标定位置；由于Δα和Δγ的值有 4种组合方式，所以在一个标定位置数N下有36× 4=144组标定位置，根据式(9)和(10)求出每组标定位置的信息矩阵行列式值，其中最大的标定位置就是该标定位置数N下的最优标定方案。

5）比较每个标定位置数N下的最优标定方案得出最终的基于D-最优的平台N位置标定方案。

惯性平台自标定不同于单表的测试，必须同时考虑陀螺仪和加速度计的输出响应。对于不同轴上的陀螺仪和加速度计而言，它们之间是初等变换矩阵的转换关系，因此对于相同的标定方案，不同轴上的陀螺仪和加速度计的信息矩阵行列式是相等的。所以在进行标定方案设计时，只需要考虑一个轴上的陀螺仪和加速度计即可，得出的最优标定方案就是所有陀螺仪和加速度计的最优标定方案[11]。由此产生了两种构造最优标定方案的思路：第一种是同时设计陀螺仪和加速度计的标定方案，然后对两种方案进行组合，得到最终的平台自标定方案，称之为并行方案设计；第二种是串行方案设计，即首先选择对加速度计或陀螺仪中的一个进行标定方案设计，然后以此方案为初始方案，以另一个的输出模型为回归方程进行方案优化，得到最终的标定方案。由于在D-最优理论中要求初始方案的标定位置数必须大于待估计参数个数，所以本文选择先对误差系数个数较多的陀螺仪进行标定方案设计，再在加速度计误差模型的基础上进行方案优化。下面就两种设计思路进行最优方案设计。

3.1 并行方案设计

并行设计方案是对陀螺仪和加速度计同时进行最优标定方案设计，然后将两个标定方案进行组合得到最终的标定方案。以加速度计为例，X加速度计的输出模型为如公式(7)所示。

则其信息矩阵为

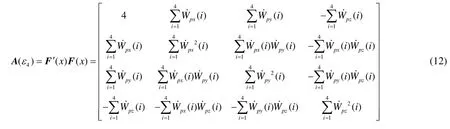
按照遍历寻优的算法流程比较信息矩阵行列式值的大小就可以得到对于加速度计的最优标定方案。不同标定方案的部分信息矩阵行列式值变化如图2所示。

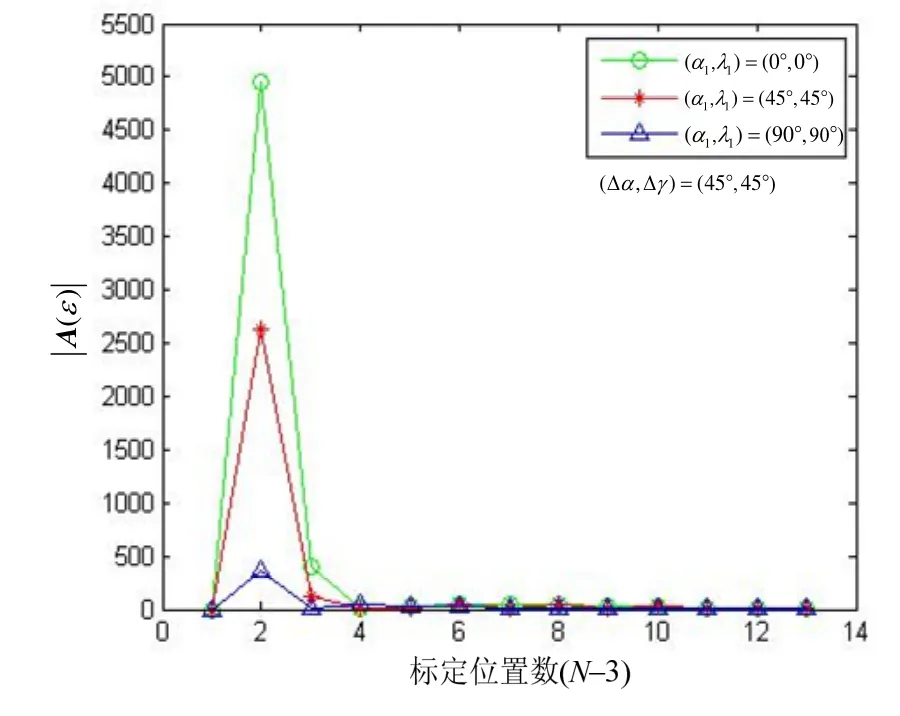
图2 信息矩阵行列式值变化图Fig.2 Change of information matrix determinant

同理可以得到陀螺仪的最优标定方案如表3所示。

表2 加速度计最优标定方案Tab.2 Optimal calibration scheme of accelerometer

表3 陀螺仪最优标定方案Tab.3 Optimal calibration scheme of gyro

将两个标定方案组合就可以得到并行方案设计下的D-最优平台自标定方案如表4所示。

表4 并行设计下的平台标定方案Tab.4 Optimal calibration scheme of platform

3.2 串行方案设计

串行方案设计是先进行陀螺仪最优标定方案的设计，然后以此方案为基础，以加速度计的输出模型为回归方程进行优化，得到最终的平台自标定方案。

在第2节中已经得到了陀螺仪的最优标定方案，在此基础上进行方案优化。此时以加速度计输出模型为回归方程可以得到信息矩阵行列式值变化如图3所示。

图3 信息矩阵行列式值变化图Fig.3 Change of information matrix determinant

表5 串行设计下的平台标定方案Tab.5 Optimal calibration scheme of platform

从图3可以看出，当N-7=2，即N=9时信息矩阵行列式值为最大，所以串行方案设计下的平台最优标定方案如表5所示。

4 仿真分析

为验证提出的标定方案设计思路的可行性，将得到的两种标定方案与文献[4]中的十六位置标定方案进行仿真对比。该十六位置标定方案如表6所示。

表6 十六位置模型Tab.6 Model of 16 position

首先给出仿真真值如表7第二栏所示。表7中：陀螺仪零次项系数单位为(°)/h，一次项系数单位为(°)/(h·g)，二次项系数为(°)/(h·g2)，安装误差单位为角秒(″)；加速度计零次项误差系数单位为 0.001 m/s2，一次项系数单位为0.001 m/(s2·g)，安装误差单位为角秒(″)；陀螺仪漂移随机误差标准差为 0.001 (°)/h；加速度计测量随机误差标准差为 1× 10-6m/s2。在标定过程中,平台框架轴安装误差认为是己知量，其仿真真值通过随机抽样产生，均值为10″，标准差为1″。

表7 仿真真值Tab.7 True values of simulation

图4 误差系数标定结果（注：图中36个误差系数依次与表7纵向相对应）Fig.4 Calibration results of three schemes

定义相对误差为

三种方案的标定结果如图4所示，表7中第三栏给出了并行方案的标定结果。从图4中对比可以看出，并行方案的标定精度明显高于串行方案和十六位置方案，而且并行方案是13位置方案，能够有效减少标定时间。从表7的并行方案标定结果可以看出，陀螺仪误差系数估计相对误差最大为 0.62%，加速度计误差系数估计相对误差最大为 0.25%，加速度计安装误差估计相对误差最大为 0.89%，估计精度都比较高。只有陀螺仪安装误差估计精度稍低，最大相对误差为8.81%，这是因为作为其激励的地球自转角速度比较小，无法充分激励误差，若要进一步激励陀螺仪安装误差，需要对平台施加加矩角速度。

5 结 论

本文首先给出了包含 36项误差系数的较为完整的惯性平台误差模型，在此基础上，针对惯性平台自标定需要同时考虑陀螺仪和加速度计的输入响应的问题，提出了两种标定方案设计思路：并行方案设计和串行方案设计。文中将惯性平台自标定看作一个广义多元回归问题，以D-最优理论为设计原则，将陀螺仪和加速度计输出模型看作广义回归方程，就两种设计思路设计出了两种标定方案。最后通过仿真分析对比两种标定方案与传统的十六位置标定方案的误差系数标定结果，证明并行方案能够以较少的标定位置(13个标定位置）达到比传统十六位置更好的误差系数估计精度，具有一定的可行性。

（References）：

[1]Seong-hoon P W, Farid G. A triaxial accelerometer calibration method using a mathematical model[J]. IEEE Transactions on Instrumentation and Measurement, 2010,59(8): 2144-2152.

[2]包为民, 申功勋, 李华滨, 等. 惯性平台在系统中多位置翻滚自标定方法[J]. 北京航空航天大学学报, 2011,37(4): 462-465.Bao Wei-min, Shen Gong-xun, Li Hua-bin, et al. Investigation on inertial platform multi-position rolling selfcalibration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 462-465.

[3]Begot S, Voisin E, Hiebel P. D-optimal experimental design applied to a linear magnetostatic inverse problem[J]. IEEE Transactions on Magnetics, 2002, 38(2): 1065-1068.

[4]Kit Yan Chana, Nimali Rajakarunaa, Ulrich Engelkeb, et al. Alignment parameter calibration for IMU using the Taguchi method for image deblurring[J]. Measurement,2015, 65: 207-219.

[5]曹渊, 张士峰, 杨华波, 等. 惯导平台误差快速自标定方法研究[J]. 宇航学报, 2011, 32(6): 1281-1287.Cao Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Research on rapid self-calibration method for inertial platform[J].Journal of Astronautics, 2011, 32(6): 1281-1287.

[6]Cao Y, Cai H, Zhang S F, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit[J]. Measurement Science and Technology, 2012,23(1): 385-394.

[7]Hajiyev C. Sensors calibration design based on D-optimal criterion[J]. Metrology and Measurement Systems, 2016,23(3): 413-424.

[8]Stuart H, Munson-McGee. D-optimal experimental designs for uniaxial expression[J]. Journal of Food Process Engineering, 2014, 37(3): 248-256.

[9]Ghasemain E, Motaghian P, Vatanara A. D-optimal design for preparation and optimization of fast dissolving Bosentan nanosuspension[J]. Adv Pharm Bull, 2016, 6(2): 211-218.

[10]Kincaid R K, Padula S L. D-optimal designs for sensor and actuator locations[J]. Computers & Operations Research,2002, 29(6): 701-713.

[11]孟卫锋, 袁爱红, 贾天龙, 等. 高精度惯性平台十六位置自标定方案[J]. 中国惯性技术学报, 2015, 23(2):150-155.Meng Wei-feng, Yuan Ai-hong, Jia Tian-long, et al.16-position self-calibration of high-accuracy inertial platform[J]. Journal of Chinese Inertial Technology, 2015,23(2): 150-155.

Design of inertial platform self-calibration scheme based on D-optimal theory

WANG Qi, WANG Li-xin, SHEN Qiang, Qin Wei-wei
(Rocket Force University of Engineering, Xi’an 710025, China)

In view that there is usually no systemic design method for the self-calibration scheme of inertial platform, a design method based on D-optimal theory is proposed to solve such problem. An error model of inertial platform with 36 error coefficients is deduced and is used as multi-regression model in designing the calibration scheme, in which the inertial platform self-calibration is regarded as a generalized multiple regression problem. Two design ideas, i.e. parallel scheme and serial scheme, are proposed for the calibration scheme based on the D-optimal theory. Simulation comparisons are made between the obtained optimized scheme and the traditional 16-position calibration scheme, and the results show that the relative error of gyro-platform geometry by the optimized scheme is about 5%, which is much lower than that of the traditional 16-position calibration scheme, and the calibration precision of the optimized scheme is better than that of the traditional scheme. In addition, the calibration time is reduced because of fewer positions.The simulation results validate the applicability of the design idea based on D-optimal theory.

D-optimal; inertial platform; self-calibration; error model; optimal position

U666.1

A

1005-6734(2016)05-0583-06

10.13695/j.cnki.12-1222/o3.2016.05.005

2016-07-01；

2016-09-17

国家自然科学基金青年基金（61503390）

王琪（1991—），男，博士研究生，从事惯性系统及仪器研究。E-mail: wq050314@163.com

联 系 人：汪立新（1966—），男，博士生导师，从事惯性系统及仪器研究。E-mail: wlxxian@sina.com