理解“整式的加减”的规则

孔凡哲　祖丹

“整式的加减”是“数与代数”领域的重要内容，是学好“一元一次方程”等其他知识的重要基础。

从人类发展的视角看，“整式的加减”的规则并非人为规定，而是解决实际问题的现实需要，对于合并同类项法则是如此，对于去括号法则也是如此。

例1如图1所示，餐厅的1个长条桌旁最多可坐6人，遇到小型聚会，餐厅老板总是按照顾客要求，将长条桌并在一起（如图2所示），按照这种方式摆x个长条桌，可以坐多少位顾客？

下面是几位同学的答案，我们一起来揭示他们思考的过程。

4同学说：“当摆x个这样的长条桌时，可以坐（2x+2x+1+1）位顾客，如图3，当摆z个长条桌时，这些长条桌的上侧可以坐2x位顾客，这些长条桌的最左边、最右边可以各坐1位顾客，这些长条桌的下侧可坐2x位顾客，所以，当摆x个长条桌时，一共可坐（2x+2x+l+1）位顾客。”

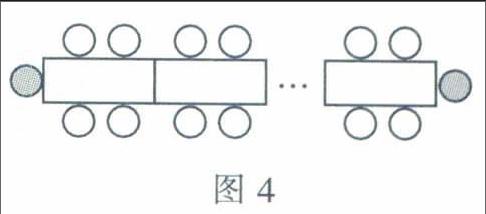
B同学说：“我的答案是2+4x，如图4，当摆x个长条桌时。最左边、最右边可以各坐1位顾客，当摆1个长条桌时，我就加上4个座位，一共可坐2+4=6（位）顾客；当摆2个长条桌时，我就加上2x4个座位，一共可坐2+2x4=10（位）顾客；当摆3个长条桌时，我就加上3x4个座位，一共可坐2+3x4=14（位）顾客，依此类推，我得到的答案就是（2+4x）位顾客。”

C同学说：“我认为，6x-2（X--1）是正确答案，请看图5，当摆1个长条桌时，可坐6位顾客；当摆2个长条桌时，有6×2=12（个）座位，但是，有2个座位是无法坐的（如图5中的阴影座位），所以，可坐6x2-2x（2-1）：10（位）顾客；当摆3个长条桌时，有6x3=18（个）座位，有无法坐的座位2x（3-1）=4（个），也就是，一共可坐6x3-2x（3-1）=14（位）顾客，因此，我得到的答案是[6x-2（x-1）]位顾客，”

D同学说：“答案应该是6+4（x-1），当摆1个长条桌时，可坐6位顾客；当摆2个长条桌时，在1个长条桌的6个座位基础上加上4个，即可坐6+4x（2—1）=10（位）顾客：当摆3个长条桌时，在2个长条桌的0个座位基础上加上4个，即可坐6+4x（3-1）=14（位）顾客，因而，摆x个长条桌就应该可坐[6+4（X-1）]位顾客，也可以理解成，只有第一个长条桌旁有6个座位，剩下的长条桌旁都只有4个座位（如图6所示），”

同一个问题，为什么答案不一样呢？谁的答案正确呢？考虑到字母x取值的任意性，我们来验证一下（参见表1），

从表1中我们可以发现，这四个整式的结果总是相同的，那么，是不是说四位同学所得的式子都相等呢？

这是我们的猜想！而且这个猜想是合理的（起码就我们验证的数字来说，是对的），同时，可以发现，在四个式子中，2+4x是最简单的，计算起来也最简单，

猜想1：2x+2x+1+1=2+4x，

思考过程：我们可以将这个多项式中的相同的项加在一起，即2x+2x=4x，1+1=2，因而，2x+2x+1+1=2+4x是有道理的，

猜想2：6x-2（x-1）=2+4x

思考过程：如果这个等式成立，那么，必然有2x-2（x-1）=2，也就是说，-2（x-1）必须等于2x+2，可以发现，去掉括号前的负号，括号内的各项的符号都要变号！

猜想3：6+4（x-1）=2+4x，

思考过程：如果这个等式成立，那么，必然有4（x-1）=4x-4，也就是说，去掉括号，括号内的各项，都要同时乘以括号前面的数字！

在上面这个问题的解决中，我们实际上“发现”了去括号法则和合并同类项法则，

如何理解合并同类项？同类项的分类标准是什么？下面我们一起来看一道例题，

例2化简多项式4x+7+x2+3x-2x2-5+y-3y。

在化简多项式时，我们需要对单项式进行分类、合并，以减少项数达到化简的目的，根据不同的分类标准得到不同的解题方法（如表2），

为了将代数式化为最简，总结表2中两种分类标准的局限性，将具有相同字母，并且相同字母的次数相同的单项式作为分类标准，可以这样化简：

（x²-2x²）+（4x+3x）+（7-5）+（y-3y）=-X²+7x+2-2y。

由此，我们可以发现，合并同类项之后，所得项的系数是合并前各同类项的系数之和，

如果多项式内有括号时，需要先将括号去掉再根据同类项的定义对其进行分类，

例如，对于多项式a（x-3）和多项式-a（x-3），类比数的乘法分配律，应该这样化简：

a（x-3）=ax-3a，-a（x-3）=-ax+3a，

根据去括号时符号的变化规律，我们得到如下口诀：

去括号，看符号，加不变，减全变。