电子相对论径向波函数的基本特征

刘晓斌，师应龙，邢永忠，路飞平

(天水师范学院 物理系，甘肃 天水 741001)



电子相对论径向波函数的基本特征

刘晓斌，师应龙，邢永忠，路飞平

(天水师范学院 物理系，甘肃 天水 741001)

利用相对论平均自洽场理论，研究了电子相对论径向波函数的基本特征.电子相对论径向波函数大小分量的数量级通常相差悬殊且不“同步”，核外电子的径向分布没有严格的零概率点；束缚电子相对论径向波函数大小分量的节点个数为n-l-1、波腹个数为n-l，而自由电子的节点和波腹数则趋于无穷大.电子相对论径向波函数反映了相对论效应的基本特征：相对论效应越强，小分量振幅相对越大，自由电子径向波函数振荡越剧烈.

狄拉克方程；相对论自洽场；径向波函数；节点；波腹

量子力学的基本原理之一，就是微观体系的状态可用希尔伯特空间的波函数完全描述，从波函数可以得到微观体系的所有性质：只要知道波函数，则体系的其他物理量如能量、截面以及跃迁概率等原则上均可确定.作为量子力学的基本方程，薛定谔方程深刻地揭示了微观世界物质运动的基本规律，打破了以往看来十分神秘的微观世界，为波动力学的建立奠定了基础.实验表明，只要微观粒子的运动速度远比光速小，薛定谔方程就是一个很好的近似，可成功地描述许多微观现象，甚至对低能核物理中的一些现象也能做出令人满意的解释.但研究高能粒子的行为须用相对论量子力学，此时描述微观粒子运动的波动方程对洛伦兹变换必须协变，而薛定谔方程中时间和空间并非对称，对时间坐标的求导为一次，而空间为二次，很显然不符合相对论协变性要求[1].狄拉克方程就是为了推广薛定谔方程使其符合相对论协变性要求而提出的，是相对论性的量子力学波动方程[2].对于高能领域如核聚变、粒子的高能碰撞以及高温等离子体等，由于粒子的速度非常高，相对论效应十分明显，此时粒子的运动须用狄拉克方程描述.

与非相对论性的薛定谔方程相似，如果将狄拉克方程中的ψ看作态的波函数，则ψ*ψ为概率密度，可将狄拉克方程作为单粒子运动的波动方程，这也能说明氢能级的精细结构等重要的物理问题.但将ψ*ψ理解为概率密度意味着在一定程度上粒子有确定的位置，根据不确定关系其动量必存在一定的不确定性，足够大的动量将使粒子的能量大于其二倍静止能量并导致粒子的产生，此时讨论单粒子的问题将失去精确的物理意义；为克服负能态的困难，狄拉克对“真空”做了新的理论解释：真空并非一无所有，真空是没有任何场量子被激发的状态，或所有的场都处于基态即为物理上的“真空”.狄拉克“真空”不空的物理思想包含了极为丰富的物理内容，任何物理上可测量到的量相当于对“真空”态的偏离.所以在相对论情形中场的概念不可避免，理论内在的自洽性要求将狄拉克方程理解为场方程，再进行量子化.尽管如此，在一些问题中如果粒子的产生和湮没等现象的影响不是很严重，狄拉克方程的单粒子理论还是取得了很大成功：狄拉克方程隐含了电子自旋，从理论上可直接得出电子存在自旋运动及内秉磁矩，并预言了正电子的存在等.正因如此，狄拉克方程在很长时间内被人们视为唯一值得信赖的相对论波动方程.

1 理论方法

原子的能量由组成原子的各粒子间的相互作用决定，而通常这种相互作用非常复杂，如果不进行必要的简化，就会使相关的理论研究变得极为困难甚至不可能.早期采用单电子零级近似：忽略了电子间的相互排斥作用，认为各电子在原子核外完全“独立”地运动，这种近似处理与客观实际相差较大,其结果必然相当粗糙.合理可行的方法就是采用独立电子的中心场模型：考虑了电子间的相互排斥作用，但将这种相互作用作了必要的理论简化处理,认为电子独立地在原子核与其他电子的平均势场中运动，其他电子对第i个电子的排斥作用从原子核发出，显然这种理论模型比单电子零级近似更接近物理实际.中心场近似为简化多电子原子提供了一个相当成功的量子力学模型，在物质结构的理论研究中得到了广泛应用.在中心场模型下，如果知道原子中相关电子的波函数，即可通过一定的理论计算而知道电荷分布，并进一步推导出其激发的平均势；根据平均势也可以计算出电子的电荷分布、进而知道波函数.这说明原子中电子的波函数与平均势相互依存并彼此制约：电子波函数所确定的平均势与由平均势所确定的波函数必须相互协调或自洽，这就是自洽场(self-consistent field,SCF)理论的物理思想.满足这个条件的微观体系的平均势能场称为自洽场，按照这种物理思想所设计的计算方法为自洽场方法.自洽场理论模型更好地考虑了电子间的相互作用，其计算结果通常具有很高精度.相对论自洽场理论本质上是独立电子的平均自洽场模型，与非相对论性自洽场理论模型下的电子波函数不同，单电子的相对论波函数为[3]

(1)

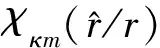
(2)

独立电子的中心场模型最多是一种理论近似(仅对氢原子严格成立，对其他原子则未必如此)：没有很好地考虑电子间的相互关联，例如减小平行自旋电子相互接近概率的泡利关联、电子间相互作用的库仑关联等[4]；原子中的相关电子除受到核的中心势外，通常还会受到自旋-轨道、核自旋、外电磁场以及电子间的相互排斥等非中心势的作用[5].在中心场近似下，电子相对论波函数的角向和径向部分可分离，分离后的相对论角向波函数对所有原子均相同，而不同原子或相同原子不同状态的相对论径向波函数通常不同，即相对论径向波函数的求解更具物理上的实际意义.当电子在中心场U(r)中运动时，狄拉克方程可表示为[2]

(3)

(4)

εnk为电子在nκ相对论次壳层的轨道能量，Vscf(r)为自洽势； 通常束缚态电子只能处于原子核外一定区域，电子在非常靠近和远离核的区域出现的概率几乎为零，而自由电子的波函数则可延伸到无穷远处.对多电子原子中的束缚电子，此方程只能通过自洽场迭代数值求解；自由电子由于其动能已知，不需通过迭代过程而只需积分即可得到波函数.一般而言，自洽场势有多种近似方法[7]，但主要为起决定作用的核吸引的库仑势、较小的电子-电子排斥库仑势以及局部交换势.

2 计算结果及讨论

利用上述理论方法，本文研究了相对论径向波函数的基本特征.主要内容包括以下两方面.

2.1 相对论径向波函数的一般特征

狄拉克方程中的波函数为4分量函数，在中心场近似下可将电子相对论波函数的角向和径向部分分离.图1是Na(1s22s22p63s)的3s电子及Na1+(1s22s22p6)的势场中动能为ε=0.001 Hartree的自由电子相对论径向波函数的大分量P(r)和小分量Q(r)；为便于比较，我们将径向波函数的小分量Q(r)乘了50(后面有类似情况)；径向距离和电子能量采用了原子物理的理论研究中通常采用的原子单位，分别为a0=0.529×10-10m 和ε0=27.211 eV=1 Hartree.可以看出：电子相对论径向波函数的大分量与小分量的数量级相差非常悬殊，在通常情况下大分量起主导作用；与非相对论的情况相同，束缚电子相对论径向波函数大小分量均有n-l-1=3-0-1=2个节点、n-l=3-0=3个波腹，当径向距离增大到一定程度时径向波函数迅速趋于零；自由电子相对论径向波函数的大小分量有无穷多个节点和波腹，在靠近核的区域波函数振幅较小，远离核时波函数振幅略有增大趋势；相对论径向波函数的大小分量明显地不同步，即在相对论情况下核外电子的径向概率分布P2(r)+Q2(r)没有严格意义的零概率点.这是因为自由电子可到达原子核外任何距离处，波函数可以延伸到无穷远，其主量子数n由于失去确定性而趋于无穷大，相对论径向波函数大小分量的节点数n-l-1及波腹数n-l即为无穷，具体表现为波函数振荡剧烈；束缚电子通常只能处于原子核附近的一定区域，其主量子数n具有确定值，相对论波函数大小分量的节点和波腹数也确定.通常情况下，自由电子由于距离原子核较远，很难靠近原子核，从而使其在近核区域的径向波函数振幅较小，这也是主量子数n较大时束缚电子波函数所具备的基本特征.

图1 Na(1s22s22p63s)的3s电子以及Na1+(1s22s22p6)的势场中动能为0.001Hartree的自由电子εs的相对论径向波函数的大小分量.为便于比较，小分量径向波函数乘了50

2.2 相对论效应较强时径向波函数的特征

束缚电子所感受到的核势场越强、自由电子的动能越大，则意味着相对论效应越明显.图2是Fe15+(1s22s22p63s)的3s电子相对论径向波函数的大小分量，由于Fe15+(1s22s22p63s)为高离化态离子，其离化度较高，核外电子所感受到的有效核电荷较一般离子(原子)的大的多，即相对论效应对电子的影响应较强.与图1中Na(1s22s22p63s) 的3s电子相比，可以发现两者3s电子的径向波函数十分相似，但Fe15+(1s22s22p63s)的3s电子的小分量径向波函数的振幅相对较大，而且径向波函数沿靠近核的空间被严重压缩.对此不难理解：较大的有效核电荷将导致相关电子只能在更靠近核的区域运动，即波函数沿靠近核的径向空间被压缩，而相对论效应的增强使径向波函数的小分量也有所增加.

图2 Fe15+ (1s22s22p63s)的3s电子相对论径向波函数

图3是动能为ε=1 Hartree和ε=100 Hartree的自由电子εp(j=1.5)在Fe16+(1s22s22p6)的势场中运动时的相对论径向波函数.通常自由电子的动能越大，相对论效应就越明显，主要表现为径向波函数振荡更为剧烈、其小分量的振幅也相对较大，而这正是图3所表示的.

图3 Fe16+(1s22s22p6)的势场中动能分别为ε=1 Hartree和ε=100 Hartree的自由电子εp(j=1.5)的相对论径向波函数

3 结论

利用相对论平均自洽场理论，研究了电子相对论径向波函数的主要特征.电子相对论径向波函数的大分量与小分量的数量级通常相差非常悬殊，且大小分量沿径向空间的变化并不“同步”；与非相对论的情形相同：相对论径向波函数的大小分量均有n-l-1个节点、n-l个波腹，但自由电子则由于其主量子数失去确定性而趋于无穷大，其节点和波腹个数必然为无穷大.通常相对论效应越强则电子相对论径向波函数小分量振幅相对地越大、自由电子波函数振荡越剧烈，而核库仑势的增强及电子动能的增大意味着相对论效应更为明显.

[1] 褚圣麟. 原子物理学 [M].北京: 高等教育出版社,1979:89-91.

[2] 柯善哲, 蔡建华. 量子力学(下)[M].北京: 高等教育出版社,1992:346-350,362.

[3] Dyall K G, Grant I P, Johnson C T, et al. Grasp: A general-purpose relativistic atomic structure program [J]. Comput Phys Commun, 1989, 55: 425-456.

[4] 唐纳德J P. 高激发原子[M].詹明生,王谨,译. 北京: 科学出版社,2003:10-11.

[5] 徐克尊. 高等原子分子物理学 [M].北京: 科学出版社,2000:93-95.

[6] 李家明, 赵中新. 变价稀土元素L,M,N内壳层电子束缚能的变化 [J]. 物理学报, 1982, 31(1)：97-103.

[7] 方泉玉, 颜君. 原子结构、碰撞与光谱理论 [M]. 北京: 国防工业出版社, 2006:144-154.

The fundamental properties of electron relativistic radial wave function

LIU Xiao-bin, SHI Ying-long, XING Yong-zhong, LU Fei-ping

(Department of Physics, Tianshui Normal University, Tianshui, Gansu 741001, China)

The fundamental properties of electron relativistic radial wave functions have been studied theoretically based on the relativistic average self-consistent field. Usually, the small-component of relativistic radial wave functions is several orders of magnitudes less than the large-component, and is not generally synchronous with the large-component, so the radial probability density of electron has no exact zeros. The number of nodes for bound electron large- or small-component isn-l-1, so that the number of antinodes isn-l, but the number of nodes and antinodes for free electron just turn to infinite. The radial wave functions are extremely sensitive to the relativistic effects, the amplitude of small-component increases with increasing relativistic effects, as well as the oscillating intensity of large, small-component for free electron.

Dirac equation; relativistic self-consistent field; radial wave function; node; antinode

2016-03-22；

2016-05-30

国家自然科学基金(11264033,11464040,11265013)、甘肃省高等学校科研项目(2014A-104)、甘肃省自然科学基金(1506RJZE112)资助

刘晓斌(1973—)，男，甘肃天水人，天水师范学院电子信息与电气工程学院物理系副教授，主要从事原子物理的教学及研究工作.

O 562.1

A

1000- 0712(2016)12- 0019- 04