一类n阶三脚架电阻网络的等效电阻研究
谭志中,陆建隆
(1. 南通大学 物理系,江苏 南通 226019;2. 南京师范大学 教师教育学院,江苏 南京 210097)
一类n阶三脚架电阻网络的等效电阻研究
谭志中1,陆建隆2
(1. 南通大学 物理系,江苏 南通 226019;2. 南京师范大学 教师教育学院,江苏 南京 210097)
研究了一类n阶三脚架网络的等效电阻模型, 该模型含有7个不同的电阻元素,因而包含了多个网络模型. 文章采用构建等效模型的方法导出了一个非线性差分方程模型,采用变量代换的方法间接地给出了非线性差分方程的通解. 本文进一步创造了一个负电阻的概念,获得了电阻网络任意节点间的等效电阻公式. 利用特殊条件下的数个特殊例子与相关结果进行了比较. 本文的结论也适用于复阻抗网络的等效复阻抗研究.
三脚架网络;等效模型;非线性差分方程;等效变换;负电阻
电阻网络模型的建立与研究已经历了170多年的历史. 自从1845年德国物理学家基尔霍夫(1824—1888)创立了节点电流定律和回路电压定律以来,人类就开始通过建立电阻网络模型解决许多抽象和复杂的科学问题[1-26].在自然科学领域与工程技术领域研究电阻网络模型具有重要的理论与实践意义, 其研究方法的创造性对于大学物理开展教学与科研协同相长教学具有很好的方法论意义,对培养大学生的创新思维能力具有较好的教学实践意义. 文献[1]系统地研究了各种类型的电阻网络模型,构建了研究电阻网络等效电阻的一系列新的理论与方法,有力地推动了人类对电阻网络模型的深入研究与应用.
文献[1-7]分别从不同侧面及用不同的方法研究了一类n阶梯形网络的等效电阻. 文献[8]研究了一类n阶矩形复阻抗网络问题, 文献[9]研究了一类n阶三角形网络的等效电阻问题. 这些研究工作推动了电阻网络等效电阻的研究与发展. 然而科学的发展不断提出新的电阻网络问题,有些新问题正在等待着研究者去解决. 本文拟研究一种新类型的含有复杂三脚架结构的n阶梯形电阻网络的等效电阻,如图1所示. 这一网络模型中含有7个独立的任意电阻元素,因而该电阻网络具有多价值功能. 本文的研究目标是获得n阶网络左端An和Bn两节点间的等效电阻公式, 以及任意Ak和Bk两节点间的等效电阻公式.
1 递推方程模型建构
图1为一般形式的n级三脚架电阻网络模型. 该网络有7个不同的任意电阻元素,即r、r0、r1、r2、r3、r4、R0.其中网络最右端的一个电阻R0可视为网络的负载. 当n→∞时,一般称该网络为无穷三脚架电阻网络.根据图1的结构特征,假设n阶网络的左端An和Bn两节点间的等效电阻为Rn,那么n-1阶网络的左端两节点间(从左端向右看)的等效电阻为Rn-1. 因此我们可以将图1简化成为图2所示的一个简单模型.

图1 一个n阶三脚架电阻网络模型,其中右端为任意负载R0

图2 二端网络等效电路模型
电路图2可以继续等效为图3(a)和图3(b)结构. 在图3(a)中计算得到

图3 二端网络中等效电阻的分级计算图
(1)
在图3(b)中计算得到
(2)
将式(1)代入式(2)中化简得到
(3)
利用图3(b)计算得到
(4)
将式(3)代入式(6)中化简得到
(5)
其中a、b、c分别为


(6)
方程式(5)是我们寻找的递推公式,此属于非线性差分方程[1-4,8,9]. 这一数学模型的物理意义是非常明确的,即对于网格数为n的梯形电阻网络,其等效电阻为Rn,当网格数为n-1个时,其等效电阻为Rn-1,当网格数为0时,其等效电阻为R0.
2 推导等效电阻公式
根据文献[1]中建立的计算非线性差分方程的方法,设存在待定数列{xn},并且xn满足如下关系:
(7)
可以规定其初始项x0=1,进而根据式(7)得到
x0=1,x1=R0+c
(8)
将式(7)及其递推式Rn-1代入式(5)化简得到
xn+1=(c+b)xn+(a-bc)xn-1
(9)
设方程式(9)的特征方程的两个根分别为α和β,则解得:
(10)
则差分方程式(9)可以重新写成为
xn+1=(α+β)xn-αβxn-1
(11)
根据文献[1]中建立的计算差分方程的方法得到
(12)
将初始条件式(8)代入式(12)化简得到
(13)
如果应用α+β=c+b(由式(10)导出), 则可以将式(13)重新写成
xn=Fn+1+(R0-b)Fn
(14)
其中
(15)
式(14)就是我们得到的差分方程式(9)的通项公式. 将式(14)及其递推式xn+1代入式(7)化简得到
(16)
将式(16)化简得到
(17)
其中αβ=bc-a由式(9)得到,并且利用了α+β=c+b. 另外,应用式(6)计算得到
(18)
式(16)和式(17)是等价的,都是一个对于r、r0、r1、r2、r3、r4、R0这7个任意电阻均成立的等效电阻公式,具有普遍意义. 这一简洁公式的发现是一次有意义的创新.
3 任意节点间的等效电阻公式
式(17)仅仅给出了计算左端An和Bn两节点间的等效电阻,我们能否计算任意节点间的等效电阻呢?本文创造性地建立了负电阻的概念,巧妙地解决了这样的问题. 设Ak、Bk分别是距离右端两节点A0、B0间隔为k个网格的两个任意节点,则有等效电阻公式
(19)
或者写成
(20)
其中
(21)
(22)
下面给出式(19)的推导过程.
我们首先建立负电阻的假设,将电阻r0等效为3个电阻的并联,如图4所示,即r0=r0//(-r0)//r0. 这是一个非同一般的等效假设,因为人类科学史上从来没有出现负电阻的概念,这一等效方法巧妙地解决了一个复杂的问题.
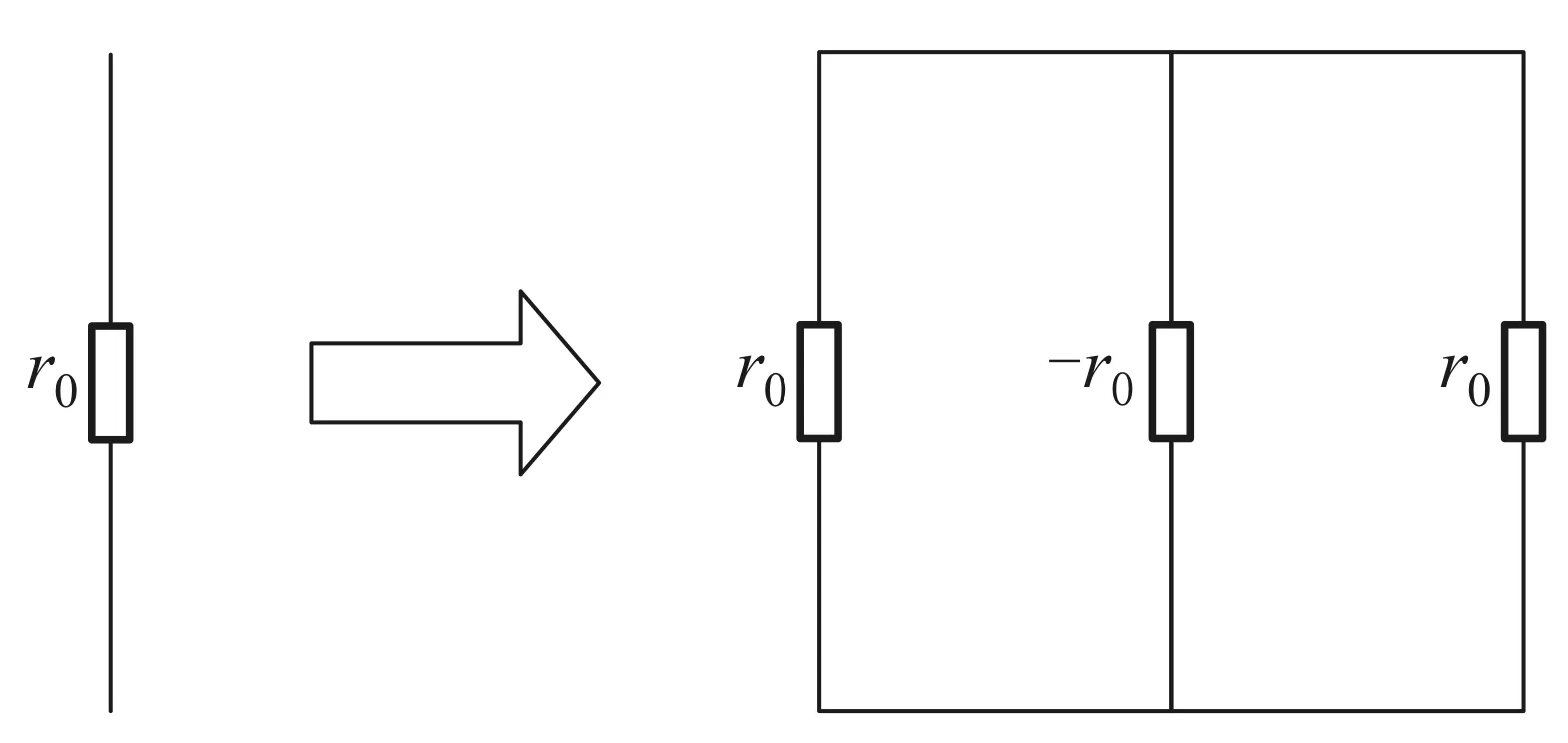
图4 一个电阻等效为3个并联电阻
为了计算任意Ak、Bk两节点间的等效电阻,在图4的等效假设之下将图1等效为图5的等效模型. 因为Ak、Bk分别是距离右端两节点A0、B0间隔为k个网格的两个任意节点,所以图5中Ak、Bk的右端有k个网格,而Ak、Bk的左端有n-k个网格. 从Ak和Bk之间的负电阻分别向左右两边考虑,记向右和向左的等效电阻分别为Rright(k)和Rleft(n-k),则根据上文得到的等效电阻公式(17)即可以得到式(21)和式(22).

图5 图1网络模型的一种等效变换模型
图5实际上是一个简单的3个电阻并联结构(其中有一个负电阻-r0),依据图5容易得到等效电阻
(23)
由此化简即得式(19),而由式(19)化简即得式(20).至此式(19)和(20)获证.
4 应用于复阻抗网络
设图1网络中的所有元素为复阻抗, 则称图1为一类n阶三脚架结构的复阻抗网络. 记图1中的复阻抗为rk(k=0,1,2,3,…). 复阻抗子网络结构如图6所示. 如果输入电压的圆频率为ω,则根据混联电路的计算规则得到等效复阻抗单元为
(24)
其中i为虚数单位,i2=-1.将式(17)中的电阻元素用式(24)取代即可以得到复阻抗网络的等效复阻抗公式.由于复阻抗的表达结构比较复杂并且需要讨论特征方程根的复数情形,此处不再给出具体公式与讨论.

图6 元素rk表达的等效复阻抗
5 数个特殊结论及应用
情形1 当r3=0及r1→∞时,图1中的网络单元退化为图7所示的双三角形结构,显然图7结构即为文献[9]中研究过的三角形电阻网络模型.

图7 内含2个三角形的子网络模型
当r3=0及r1→∞时,由式(6)中的3个等式取极限得到
(25)
则由结论式(17)得到
(26)
其中Fn=(αn-βn)/(α-β),b由式(25)给出, 并且由式(10)得到
(27)
其中d=(r0+r)(r2+r4)+r2r4.通过对比发现结论式(26)与文献[9]中的结论完全一致,这就间接地验证了结论式(17)的正确性.
情形2 当r3=0,r1=r2=∞时,图1中的网络单元退化为图8所示的矩形结构,这是一类常见的n阶矩形电阻网络模型.

图8 一个n阶矩形网络的子网络模型
由于r1、r2→∞相当于断路(等效于去掉r1、r2),所以r1、r2→∞时的物理意义是,原三脚架电阻网络退化成为一般的n阶矩形网络. 由式(6)取极限得到
a=r0(r+r4),b=r0,c=r0+r+r4
(28)
则由结论式(17)得到
(29)
图8的网络模型已经被不少文献研究过,如文献[1]的研究, 比较式(29)与文献[1]中的结果可以发现2种结论完全相同. 这就再次间接地验证了结论式(17)的正确性.
情形3 当r0=r1=r2=r3=r4=r时,由式(6)化简得到
(30)
代入式(10)得到
(31)
则由式(17)得到
(32)
情形4 当r=0,r2=∞时,图1中的网络单元退化为图9结构.

图9 一类二端梯形网络的子网络模型
当r=0,r2=∞时,由式(6)取极限得到
(33)
代入式(18)得到
(34)
因此由结论式(17)得到
(35)
情形5 当r0=∞,r4=0时,图1中的网络单元退化为图10结构.

图10 一个n阶三角形网络的子网络模型
由于r0→∞相当于断路(等效于去掉r0),所以r0→∞时的物理意义是,原三脚架电阻网络退化成为一类n阶三角形电阻网络.
当r0=∞,r4=0时,由式(6)取极限得到
(36)
代入式(18)得到
(37)
则由结论式(17)得到
(38)
其中Fn=(αn-βn)/(α-β),并且b由式(36)给出.
情形6 当n→∞时,由式(10)得到0<β/α<1,故对式(17)取极限得到
(39)
其中a、b、c由式(6)给出. 结论式(39)说明式(17)是有界的.
情形7 当R0=b时(b由式(6)给出),由式(17)得到
(40)
其中α、β由式(10)给出,公式(40)是一个比较有趣的简单结果.
情形8 当R0=b-β时,由式(17)化简得到
(41)
另外,当R0=b-α时,由式(17)化简得到
(42)
其中b由式(6)给出.式(41)、式(42)都是有限常数,表明b-α及b-β是该网络的特征电阻值,与网络的阶数n无关.
6 小结与简评
本文研究了一类三脚架结构的电阻网络模型,如图1所示. 这一网络模型中含有7个独立的电阻元素,因而该电阻网络具有多价值功能. 本文采用构建等效模型的方法通过简单的计算而建立了一个非线性差分方程模型,为了研究非线性差分方程的通解,我们采用变量代换的方法间接地给出了非线性差分方程的通解,进而导出了左端节点的等效电阻公式. 为了获得电阻网络中任意节点间的一个等效电阻公式,本文创造了一个负电阻的概念,将一个电阻等效为3个并联电阻,利用前文得到的结论应用于计算任意节点间等效电阻,获得了理想的等效电阻公式. 需要强调的是目前的现实世界中还没有真正的“负电阻”,“负电阻”概念是创造的一种辅助技巧相当于几何证明中引进的辅助线,另外“负电阻”还可能相似于“数学中的虚数”,看上去没有用其实能够帮助人们解决许多复杂的问题. 当然不排除未来发现的暗物质中存在“负电阻”. 根据任意电阻可能存在的不同条件而给出了数个特殊例子,通过比较而间接地验证了本文结论的正确性. 当然,由于本文的理论推导是严密和精确的并且是自洽的,因而得到的结论必然是正确的. 本文的结论也适用于复阻抗网络的等效复阻抗研究,根据电路元件在计算中的对应关系自然地得到纯电容网络的等效电容公式. 本文的研究工作对大学物理开展教学与科研协同相长教学具有很好的指导意义,对培养大学生的创新思维能力具有较好的教学实践意义.
[1] 谭志中. 电阻网络模型[M]. 西安电子科技大学出版社, 2011:3-160.
[2] 李建新, 刘栓江.N级梯形电阻网络的研究[J]. 大学物理, 2003, 22 (7):20-21.
[3] 陆建隆, 谭志中. 关于梯形网络等效电阻的普适研究[J]. 大学物理, 2001,20 (10): 26-28.
[4] 谭志中, 陆建隆. 二端梯形网络等效复阻抗的普适研究[J]. 大学物理,2009,28 (7): 29-33.
[5] 李永安. 梯形网络等效电阻网络分析的再研究[J]. 大学物理, 2003,22(10):12-14.
[6] 谭志中, 赵素英.N阶电阻网络等效电阻的普适研究[J]. 河北师范大学学报(自然科学版), 2004,28(2):149-154.
[7] 汤华,谭志中.n阶网络任意节点的等效电阻的研究[J]. 大学物理, 2012,31 (11): 18-22.
[8] 谭志中, 陆建隆. 建构非线性数列模型研究二端梯形网络等效值[J]. 河北师范大学学报(自然科学版), 2001,25(3):339-344.
[9] 谭志中,杨建华. 一类含有复杂电阻的n阶三角形网络的等效电阻公式[J]. 大学物理, 2015,34 (6): 24-26.
[10] 谭志中,罗礼进. 2×n阶电阻网络等效电阻的再研究[J]. 南通大学学报(自然科学版),2010,9(1):86-89.
[11] 谭志中,方靖淮. 3×n阶电阻网络等效电阻的研究[J]. 大学物理,2008,27(9):7-10.
[12] 谭志中,罗达峰,杨建华. 3×n阶电阻网络等效电阻的再研究[J]. 南通大学学报(自然科学版),2011,10(2):67-72.
[13] 谭志中,罗达峰. 4×n阶网络的2个等效电阻公式[J]. 南通大学学报(自然科学版),2011,10(3):87-94.
[14] 谭志中. 半无穷矩形网络边界上的等效电阻和电流分布[J]. 南通大学学报(自然科学版),2015,14(4):70-74.
[15] 谭志中,陆建隆. 多边形电阻网络等效电阻的统一建构[J]. 河北师范大学学报(自然科学版), 2011,35(2):140-144.
[16] 谭志中. 加强型多边形电阻或电容网络的等效值研究[J]. 大学物理,2011,30(12):29-32.
[17] 谭志中. 二阶方阵N次幂的普适公式与应用 [J]. 南通大学学报(自然科学版),2012, 11(2):60-68.
[18] Wu F Y. Theory of resistor networks: the two-point resistance [J]. J Phys A: Math Gen, 2004, 37: 6653.
[19] Tan Zhi-Zhong, Essam J W, Wu F Y . Two-point resistance of a resistor network embedded on a globe [J]. Physical Review E, 2014, 90:012130.
[20] Essam J W, Tan Zhi-Zhong, Wu F Y. Resistance between two nodes in general position on anm×nfan network [J]. Physical Review E,2014, 90:032130.
[21] Tan Zhi-Zhong. Recursion-transform approach to compute the resistance of a resistor network with an arbitrary boundary [J]. Chin Phys B, 2015, 24 (2):020503.
[22] Tan Zhi-Zhong. Recursion-Transform method to a non-regularm×ncobweb with an arbitrary longitude[J]. Scientific Reports,2015(5):11266.
[23] Tan Zhi-Zhong. Recursion-transform method for computing resistance of the complex resistor network with three arbitrary boundaries [J]. Physical Review E, 2015, 91:052122.
[24] Tan Zhi-Zhong,Fang J. -H. Two-point resistance of a cobweb network with a 2r boundary [J]. Commun. Theor Phys, 2015, 63:36-44.
[25] Tan Zhi-Zhong,Zhang Q H. Formulae of resistance between two corner nodes on a common edge of them×nrectangular network [J]. Int J Circ Theor Appl, 2015, 43:944-958.
[26] Tan Zhi-Zhong, Ling Zhou, Da-feng Luo. Resistance and capacitance of 4×ncobweb network and two conjectures [J]. Int J Circ Theor Appl, 2015, 43:329-341.
A study of the equivalent resistance of ann-step network with tripod structure
TAN Zhi-zhong1, LU Jian-long2
(1. Department of Physics, Nantong University, Nantong, Jiangsu 226019, China; 2. College of Teacher Education,Nanjing Normal University, Nanjing,Jiangsu 210097,China)
We study the equivalent resistance of ann-step network with tripod structure,which is a profound problem, has not been resolved before. The network model contains seven arbitrary parameters which make the network contain a number of different types. First of all, we establish a nonlinear difference equation by means of simplifying a complex graphics into a simple equivalent model; next, we construct the method of equivalent transformation to obtain the general solution of the nonlinear difference equation. Finally, we create a new concept of negative resistance for the needs of the equivalent conversion, and obtain two general resistance formulae of ann-step network with tripod structure. We compare several results by making use of a number of specific examples in the special conditions. Our method and the results are suitable for the research of complex impedance network as well.
tripod structure network; equivalent model; nonlinear difference equation; equivalent transformation; negative resistance
2015-12-03;
2016-03-16
南通大学自然科学类科研基金前期预研项目(15ZY16);南通大学教学改革研究项目“大学物理教学与科研相长模式研究”(2015B01)资助
谭志中(1965—),男,江苏兴化人,南通大学教授,硕导,主要从事理论物理研究和物理教育研究工作.
教学讨论
O 441.1, TN 711.3
A
1000- 0712(2016)12- 0013- 06

