关于柔软细绳运动问题中加速度奇点的讨论

路峻岭，秦联华，任乃敬

(清华大学 物理系，北京 100084)



关于柔软细绳运动问题中加速度奇点的讨论

路峻岭，秦联华，任乃敬

(清华大学 物理系，北京 100084)

柔软细绳的运动问题是大学物理力学课在“质点系的动量定理”的教学中常常涉及的典型类型之一， 柔软细绳是日常实际绳索的简化的理想模型. 而理想模型的引入有时会出现在研究对象的某些点处的加速度变为无穷大，可称之为奇点. 若不考虑加速度奇点的影响常常产生错误.本文借助柔软细绳运动的一个实例对此加以讨论.

物理模型；加速度奇点；柔软细绳；质心

1 问题的提出

国内流行的不少大学物理教科书在力学之“质点系的动量定理”的教学内容中，常常在例题或习题中引入柔软细绳的运动问题.所谓柔软细绳指的是直径可忽略、长度一定、质量均匀分布且十分柔软的线段状模型， “十分柔软”指的是在无张力存在时它可以任意弯折或收缩，例如竖直静止的柔软细绳在重力的作用下可以自动地被压缩为一点(如图1(e)).柔软细绳是日常实际绳索的简化的理想模型.

下面是此类问题的几例，如图1所示.设每条细绳的质量均以m表示，位形参数均以x表示，单位长度柔软细绳的质量均以ρ表示.为了显示清晰，其中“柔软细绳”都被画成了有一定粗细的绳索.图1(a)表示[1-3]:长2l的柔软细绳AB挂在一水平光滑细圆轴钉上，由平衡静止状态起，经A端的一个向下的微小扰动后，在重力和轴钉力的作用下绕轴钉滑落.求柔软细绳刚刚脱离轴钉时的速率和在整个滑落过程中轴钉受到细绳的力.图1(b)表示[1]:长l的柔软细绳AB，B端固定，A端自由，两端并排放置，研究自由端A由静止开始下落直至细绳整体处于竖直状态的过程，求固定端在此过程中受到的细绳的力. 图1(c)表示[2]:长l的柔软细绳AB盘缩于距离地面l的水平光滑桌面上，其一端A处刚好有一光滑小孔，A端穿过小孔漏下少许，在重力的作用下柔软细绳会通过小孔向下滑落，求柔软细绳AB从开始下滑起至其整体落到地面上的一刻止所需要的时间. 图1(d)表示[1]: 长l的柔软细绳AB， 堆缩于水平光滑桌面上，其上端A在力F的作用下以速度v0匀速上升，求在此过程中力F的大小.图1(e)表示[4-6]]：长l的柔软细绳AB，A端由一力拉着，竖直地静止于一水平桌面之上，其下端B刚刚与桌面接触，突然A端的拉力消失，柔软细绳将在重力的作用下下落.求下落过程中桌面受到的柔软细绳的作用力.

若给出一定的初始条件，此类问题皆可得到解析解. 但此处柔软细绳理想模型的引入使得在研究对象的某些点处的速度有跃变从而加速度变为无穷大，可称之为加速度奇点.例如，对图1(e)所示竖直柔软细绳自由下落过程，我们用类似画波形图的方法画出某时刻细绳上各质元的位矢、速度和加速度，如图2所示，其中，横轴x′(设B为原点)表示细绳上质元的坐标，空心箭头表示过程发展的趋势.

从图2中可见，柔软细绳上随质元位置的变化，位矢是连续的，速度有跃变，加速度出现奇点(无穷大).其他各例亦有类似情况.若不考虑加速度奇点的影响常常产生错误.对求解此类问题，文献[4，5]中均有“质心加速度的计算颇有微妙之处，如不注意容易弄错.”的提示，并且建议尽量避开质心加速度的计算.其所谓‘微妙之处’的含义就在于此.近几年来，对此类问题持错误理解的文章时有发表[7，8]，因此，有必要予以纠正[9].

本文借助柔软细绳运动的一个实例(图1(a))对此加以说明.在该例中，圆轴钉半径趋于0是其重要特征，轴钉圆周趋于其圆心点，据此可忽略环绕轴

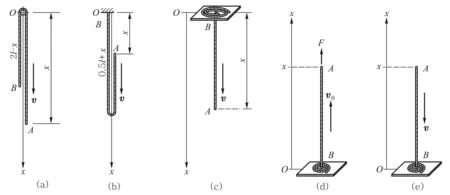
图1 柔软细绳运动问题的几例

图2 柔软细绳垂直自由下落时绳上质元的位矢u、速度v及加速度a

钉的绳元质量的影响，例如柔绳在圆轴钉两侧的张力可认为是相等的.为了叙述方便，有时要把轴钉截面画为一个具有一定半径的圆，本例指的是此圆半径趋于0的极限情形.在圆轴钉半径趋于0的极限情况下，绕轴钉运动的绳元速度方向的渐变成了速度方向的突变.

2 绕光滑水平细圆轴钉滑落的柔软细绳运动问题的几种解法

面对一道物理题，首先要做的不是马上就进行计算，而是根据题意在脑中形成正确完整的物理图像.否则，即使得到了正确的解析解它也不一定能够被理解，如在狭义相对论中洛伦兹变换是洛伦兹首先得到的，而正确理解它的却是爱因斯坦.

具体到本例，柔软细绳上相邻质元间没有收缩形变且绳上各点的速率相同，细圆轴钉光滑，所以整个滑落过程没有能耗，柔软细绳的机械能守恒.柔软细绳绕水平光滑细圆轴钉的滑落过程是初速度为零、加速度从零开始越来越大(最大为重力加速度g)的过程.轴钉两侧长短绳段在同步加速，而跨过轴钉的绳元的速度突然反向，轴钉两侧长短绳段的拉力(柔绳的张力)与轴钉力的合力是使柔软细绳元在轴钉处速度反向的力， 合力在轴钉圆周径向的分量即是使其绕轴钉作圆周运动的向心力.当柔软细绳运动的速率增大到一定值时，柔软细绳的张力自身就可以使绕轴钉运动的柔软细绳元的速度绕轴钉后而反向(不需要轴钉向上的力)，此时轴钉受到细绳向下的力为零，柔软细绳即开始与轴钉脱离接触.从此时刻起，柔软细绳元已经不能再绕圆轴钉作圆周运动了，欲使后续的柔软细绳元继续作圆周运动，需要轴钉对柔软细绳元施以向下的力(本题给出的轴钉不可能提供)，除非“柔软细绳最初绕细圆光滑轴钉悬挂”的条件改为“柔软细绳最初穿过一个半径很小的细光滑半圆形沟槽悬挂” (光滑半圆形沟槽)，只有沟槽才能够对经过它的柔软细绳元施以向上或向下的力以使它保持作圆周运动.所以在本题中， 柔软细绳的尾部在尚未到达轴钉时，贴近轴钉的绳元就已经开始脱离轴钉了.

根据题意可先作一些简单的计算，以期对柔软细绳滑落的主要特征性物理量有所了解.

据图1(a)， 若柔绳尚未脱离轴钉，则位形参数为x时的柔软细绳质心的坐标为

(1)

由初始平衡位形(x=l)到位形参数为x时，柔软细绳质心的下降高度为

(2)

由于柔软细绳滑落过程无能耗，根据机械能守恒计算柔软细绳的滑落速率.由

进而得柔软细绳的滑落速率

(3)

而速率不是速度，但可以根据速率来确定速度. 柔软细绳长侧段(x)的速度沿正x方向， 柔软细绳短侧段(2l-x)的速度沿负x方向，速度的大小均由式(3)表示.

将式(3)对时间求导，可得到柔软细绳的滑落加速率(加速度的大小)：

(4)

但加速率亦不是加速度，类似关于速度的描述，柔软细绳长侧段(x)的加速度沿正x方向， 短侧段(2l-x)则沿负x方向，加速度的大小均由式(4)表示.特别需要指出的是，绕轴钉滑过的柔软细绳元的速度由-v变为v，其加速度ao大小为无穷大(奇点)，方向沿正x方向，见下式：

(5)

由于圆轴钉半径趋于0， 与轴钉相接触的半圆形绳元为小量，它的加速不会使与轴钉相切的两点处的柔软细绳的张力值有差别，两边的张力相同，设为FT.可借助于式(4)把FT求解出来，它的大小FT可由下式表示：

(6)

当然，也可以通过长侧段(x)的动力学方程求FT，结果是一样的.

2.1 质心运动定理法

本问题用质心运动定理法求解最为简捷. 将式(1)对时间求导可以得到质心速度vc：

(7)

质心速度亦可以通过加权平均法求得：

将式(7)对时间求导可以得到质心加速度ac：

(8)

质心加速度亦可以通过加权平均法求得，但必须考虑到加速度奇点的影响.在通过加权平均法求质心加速度的过程中，加速度奇点的权为

(9)

它乘以式(5)即是加速度奇点对质心加速度的贡献.据此用加权平均法求得质心加速度：

(10)

设在柔软细绳的滑落过程中，轴钉受到细绳的向下的拉力为F，则细绳受到的力只有两个:重力FG和轴钉施予细绳的向上的力-F.且FG=mg.根据质心运动定理，列出动力学方程:

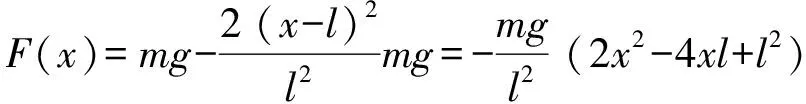
(11)

根据式(11)画出F随x的变化曲线如图3所示[7].图中AB段表示细绳接触轴钉滑落，BD段表示细绳

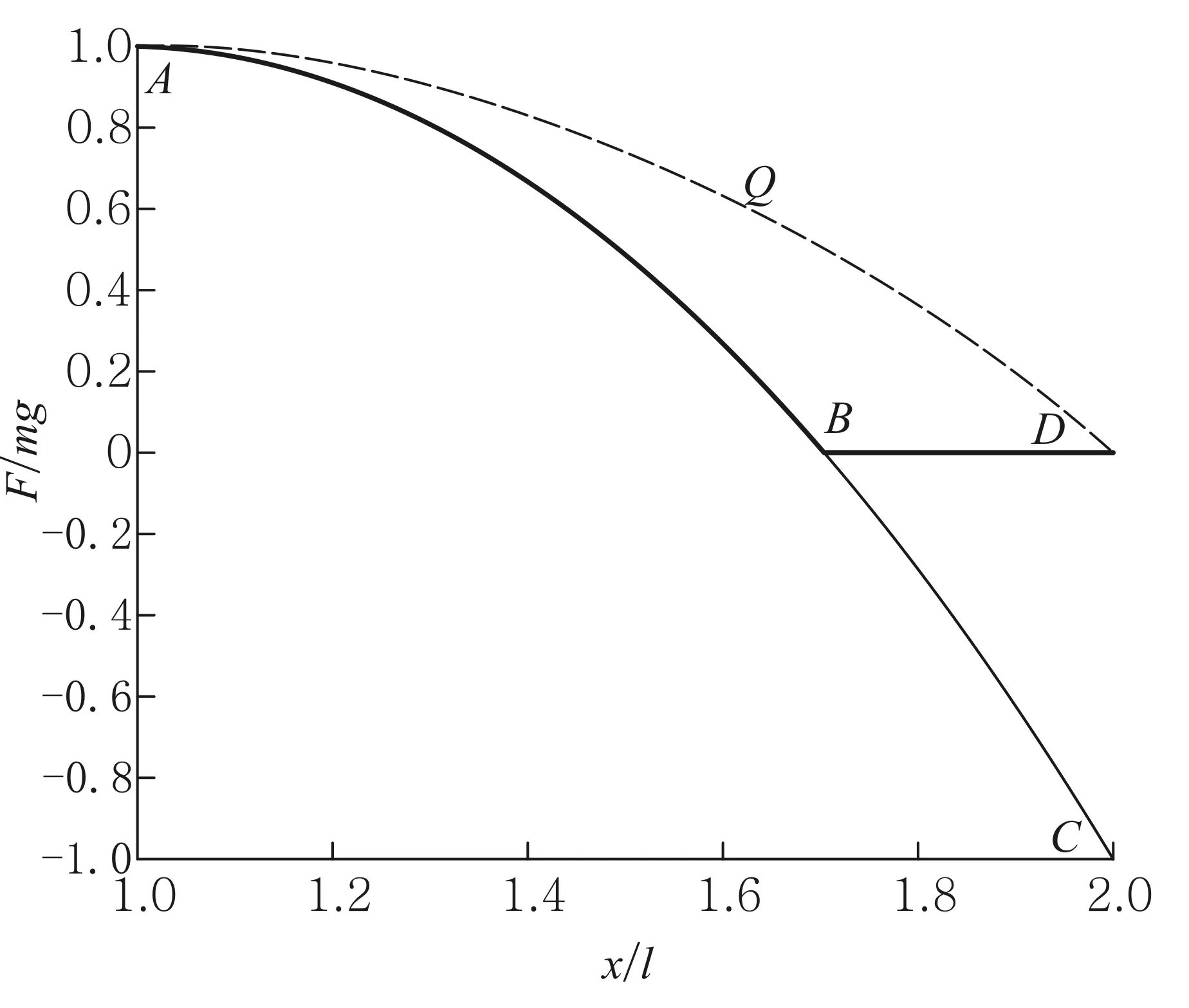
图3 轴钉受到向下的力F随x的变化曲线

脱离轴钉后的情形.曲线ABC表示若细绳通过光滑的小半圆形沟槽滑落的情形.求出B点的坐标值xB即可求出柔软细绳刚刚脱离轴钉时的速率.令式(11)为零，解此方程可得到在x>l条件下的解.

将它代入式(3)，可得柔软细绳刚刚脱离轴钉时的滑落速率：

(12)

其实， 柔软细绳刚刚脱离轴钉时的速率亦可通过对绕轴钉绳元作动力学分析得出[2].如图4所示，设绳

图4 跨过轴钉的绳元的动力学分析

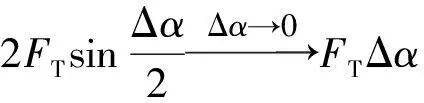
FT(x)=ρv2(x)

(13)

这便是绳元刚刚脱离圆轴钉时的临界方程.注意临界张力与绳元作圆周运动的半径无关.故在本题中，在细轴钉处若柔软细绳元段满足该式时，柔绳就会脱离轴钉.求解式(3)、式(6)、式(13)联立方程组得

此即柔软细绳刚刚脱离轴钉时的速率vB，与式(12)相同.

总之，本题的答案是：

若柔软细绳绕轴钉滑落时，则轴钉受到向下的力为

(14)

柔绳刚刚脱离轴钉时的速率为

(15)

如果把绕光滑细圆轴钉换成通过光滑小半圆形沟槽进行柔软细绳的滑落实验，结果是：

沟槽受到向下的力为

(16)

柔绳刚刚脱离沟槽时的速率为

(17)

2.2 按变质量物体处理法

本例题可按变质量物体处理法求解.在图1(a) 中，设想用一含x轴且垂直于柔绳的平面把柔绳分为两部分，左侧短段 (2l-x)，在重力和轴钉向上的力(设为F1)的共同作用下，沿负x方向加速运动，且其上端的绳元以速度突变为零的方式而湮灭；右侧长段 (x)，在重力和轴钉向上的力(设为F2)的共同作用下，沿x方向加速运动，且上端总有绳元以速度由零突变为v(x)而加入到右侧长段的运动中来.以下分别求解.

左侧短段 (2l-x)的情形见图5(a)，设其初始时长度为(2l-x)，速度为[-v(x)]，动量即为[-(2l-x)ρv(x)].经过时间Δt，湮灭掉的绳段长v(x)Δt，本绳段的速度变为 [ -v(x)-a(x)Δt]，动量变为[2l-x-v(x)Δt]ρ[-v(x)-a(x)Δt].其间该绳段的受力为重力和轴钉的向上的作用力F1.据动量定理：

[2l-x-v(x)Δt]ρ[-v(x)-a(x)Δt]-

(2l-x)ρ[-v(x)]=[(2l-x)ρg-F1]Δt

忽略高阶小量，由此式解出

F1=(2l-x)ρ[g+a(x)]-v2(x)ρ

(18)

图5 按变质量物体处理法求解

右侧长段(x)的情形见图5(b)，设初始时长度为(x)，速率为(v(x))，动量即为ρxv(x).经过时间Δt，由上端加入的绳段长为v(x)Δt，本绳段的速度变为[v(x)+a(x)Δt]，动量变为[x+v(x)Δt]ρ[v(x)+a(x)Δt].其间该绳段的受力为重力和轴钉的向上的作用力F2.据动量定理：[x+v(x)Δt]ρ[v(x)+a(x)Δt]-xρv(x)=[xρg-F2]Δt忽略高阶小量，由此式解出

F2=ρx[g-a(x)]-ρv2(x)

(19)

根据牛顿第三定律，轴钉受到柔绳向下的力为

F=F1+F2

将式(3)、(4)代入，最后得

(20)

结果与式(11)相同，进一步的分析不再重复.

2.3 直接对绕轴钉滑过的绳元进行分析法

如图6所示，设在时间Δt内，绳元Δm=ρΔx=ρv(x)Δt绕轴钉滑过，其速度由(-v(x))变为v(x)，为显示出它绕轴钉的运动，在图中轴钉被画得较大，实际上绕轴钉的半圆形微段是更高阶的小量，据此则其加速度为

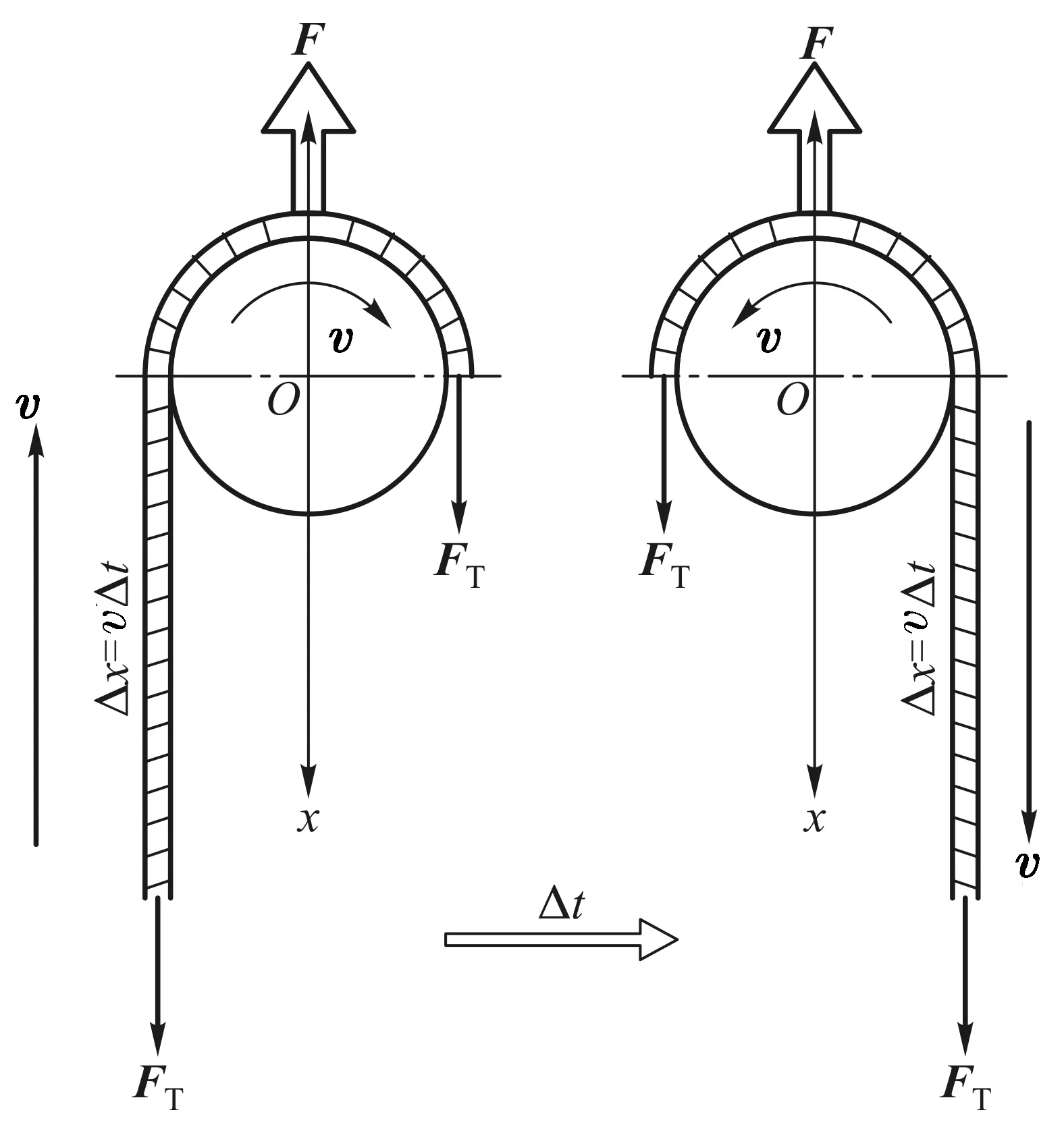
图6 瞬间改变运动方向的绳元的动力学分析

且绳元Δm共受到4个力:两端各受到其他绳段提供的张力FT(x)，轴钉向上的支撑力F和绳元重力FG(FG=Δmg).根据牛顿第二定律，沿x方向列出方程：

令Δt→0，方程化为2FT(x)-F=2ρv2(x)，即得F=2FT(x)-2ρv2(x).把式(3)、式(6)代入该式，整理可得

(21)

结果亦与式(11)相同，进一步的分析亦不再重复.

3 对柔软细绳绕水平光滑细圆轴钉滑落问题的进一步讨论

设有一个由N个质点组成的质点系，其第i个质点的质量为mi，位置坐标为xi，则其质心坐标xc，质心速度vc，质心加速度ac，可按下列三公式由上至下依次求出，这是不会出错的.

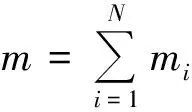
如果忽略含加速度奇点的一项，则由式(10)计算得质心加速度值就会减少一半，即为式(10)的二分之一，据此再按照质心运动定理求解，就会得到结果：

(22)

根据此式画出F随x的变化曲线如图3中曲线AQD所示.文献[7]花费大量篇幅论述该结果的合理性. 由式(9)知，加速度奇点的权是趋于零的，故它非常容易被忽略， 忽略它之后即得式(22).此式易被人接受的另一个原因是当x→2l时F=0，既然柔绳都要整个离开轴钉了，对轴钉的作用力为零似乎很合理.但力F在x=2l处有跃变，如同图1(e)柔软细绳垂直自由下落实验中桌面支持力FN在x=0处也有跃变一样，当由x>0到x=0时FN等于细绳所受重力的3倍，一旦细绳完全落到桌面上，FN只等于细绳重力的一倍.认为式(22)正确的根本原因是未能理解加速度奇点的影响.

在用“直接对绕圆轴钉滑过的绳元分析法”求解时(见图6)，若误以为图中两倍FT(柔软细绳张力)等于柔软细绳所受的重力，也会得到式(22)所示的错误解[7].原因是：用绳子系一重物，若重物静止或作匀速运动时，绳上张力才等于重物所受的重力，若重物作加速运动时则绳上张力就不再等于重物所受的重力了.

加速度奇点被忽略的一个典型对应模型如图7所示[7]，就是用一段轻质细绳跨过一个质量可以忽略的光滑滑轮，细绳两端再分别连接到质量分别等于长短柔软细绳段的两个质量块上，且它们一同以加速度a作加速运动，则滑轮受到细绳的向下的力即为式(22).该模型的关键是去除了有质量的绳元速度突变而产生的加速度奇点.

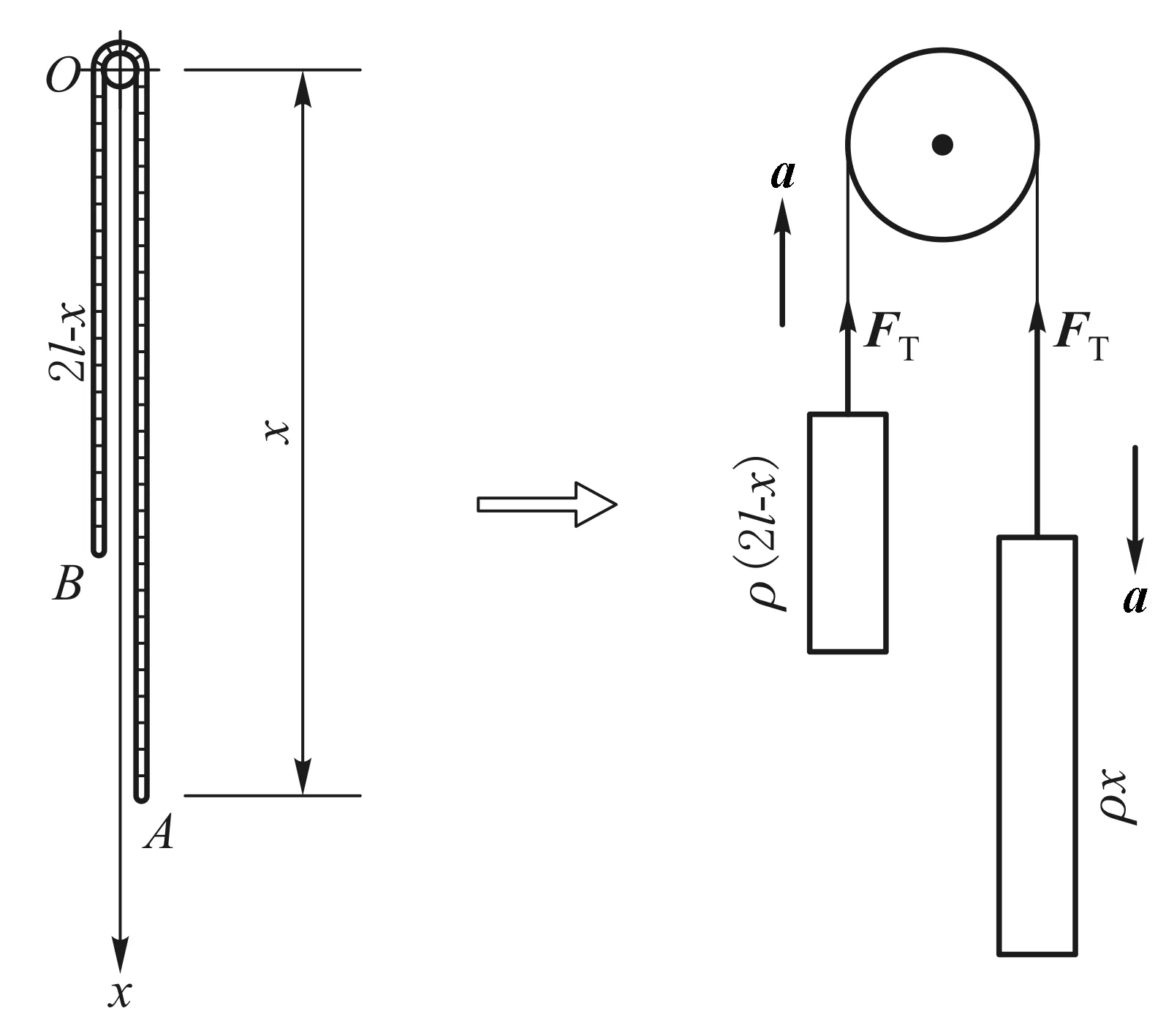
图7 柔绳滑落问题的一种错误对应模型

误以为式(22)为真的另一个陷阱是所谓实验验证，证明当x=1.707l时柔软细绳不会脱离轴钉，进而认为：由x=l至x=2l，柔软细绳在轴钉上一直在接触轴钉作绕轴钉运动，绳元经半周后速度反向[7].确实，牛顿力学的许多问题都可以通过实验来验证，但本问题却不可以.其中的原因是由它的条件所决定的: 起始，x=l时柔软细绳处于力学平衡状态，轴钉受到的压力最大(mg)，绳和钉之间一定的微小摩擦系数μ就可产生阻碍细绳滑落的具有一定值的摩擦力(μmg)(有限大量)，绳段的微小扰动(无穷小量)不会启动柔绳的滑落运动.除非μ=0严格成立，而自然界中这样的柔软细绳和光滑轴钉是不存在的.在这里，首先需要的不是基于实物的实验验证，而是人脑中的理想物理实验.

特别需要指出的是，对柔软细绳绕光滑细圆轴钉滑落问题的正确理解早已有之[2]，但他们的叙述过于简练且没有指出问题的要害是加速度奇点的存在，从而未能为人们所理解和接受.

4 结论

柔软细绳的运动问题中，加速度奇点是引入理想模型而产生的结果.严格地按照质心坐标定义求其质心坐标，将其对时间求导计算质心速度，再对时间求导计算质心加速度等运算都不会出错，有时出错就错在用加权平均法时忽略了权趋于零的加速度奇点的影响.除此之外，对物理图像的理解也至关重要.碰见问题首先要在脑中建立起研究对象运动的正确的物理图像再进行具体计算，是非常必要的.

[1] 郑永令，贾起民，方小敏.力学[M] .2版. 北京：高等教育出版社，2002:119，199.

[2] 纳德，等.200道物理学难题——附提示与解答 [M]. 李崧，等，译. 北京：北京理工大学出版社，2008：21-22:题103，题105;147-151: 题解103，题解104，题解105.

[3] 程稼夫.中学奥林匹克竞赛物理教程力学篇[M].合肥：中国科技大学出版社，2002:133-134.

[4] 梁昆淼.力学[M] .4版. 上册. 北京：高等教育出版社，2010: 188-191.

[5] 刘斌. 力学[M] .2版. 合肥：中国科学技术大学出版社，2013: 142-145.

[6] 李复. 力学教程(上)[M] .北京：清华大学出版社，2011:155-156.

[7] 刘斌. 充分发挥习题的作用培养学生独立解决问题的能力[J]. 物理与工程，2014，24(4):11-19.

[8] 赵素芬，张德明，陈子瑜，等. 2009年全国高等学校物理基础课程教育学术研讨会论文集[M]. 北京：清华大学出版社，2010:37-39.

[9] 路峻岭，秦联华，王长江. 对用动量定理解柔软细绳问题陷阱的探究[J]. 大学物理,2011，30(2)：5-8.

A discussion about the acceleration strange point in some questions of soft and thin cords’ movement

LU Jun-ling,QIN Lian-hua，REN Nai-jing

(Department of Physics, Tsinghua University, Beijing 100084, China)

Questions involving soft and thin cords’ movement are a kind of model of college physics. A soft and thin cord is an ideal model for the actual one, which makes the acceleration be infinite at some point of the soft and thin cord. This is the acceleration strange point. If the acceleration strange point is neglected, some mistakes may arise. A discussion is given here by an example of a soft and thin cord.

physics model; acceleration strange point; soft and thin cord; center of mass

2015-12-21；

2016-04-04

路峻岭(1946—)，男，河北南宫人，清华大学物理系教授，主要从事大学物理教学和传感器敏感元件物理学的研究工作.

O 313.2

A

1000- 0712(2016)12- 0007- 06