微分几何法求解单位矢量的空间导数

罗宏超，鞠丽平

(沈阳航空航天大学 理学院，辽宁 沈阳 110136)



微分几何法求解单位矢量的空间导数

罗宏超，鞠丽平

(沈阳航空航天大学 理学院，辽宁 沈阳 110136)

利用微分几何与矢量极限的方法及坐标系间的关联推导了常见曲线坐标系中单位矢量的空间导数.推导过程简洁直观，便于理解，方便在物理教学及实践中运用.

单位矢量； 微分几何； 曲线坐标； 空间导数

在理论物理及其工程应用中经常需要计算矢量的导数，曲线坐标系中由于单位矢量的方向变化，需附加单位矢量的空间导数或时间导数[1,2]，一般采用正交曲线坐标系进行求解[3-6]，过程严谨，通用性好，但需要一定的数学基础，求解方法比较抽象.

利用微分几何的方法[7,8]，考虑极坐标与柱坐标和球坐标的关联，可以直观形象地求解常用曲线坐标系下单位矢量的导数问题，对于正确理解矢量的偏导数及偏微分方程有重要意义.

1 极坐标系下单位矢量的空间导数

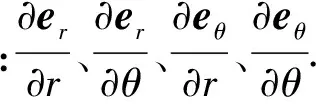
(1a)

(1b)

(1c)

(1d)

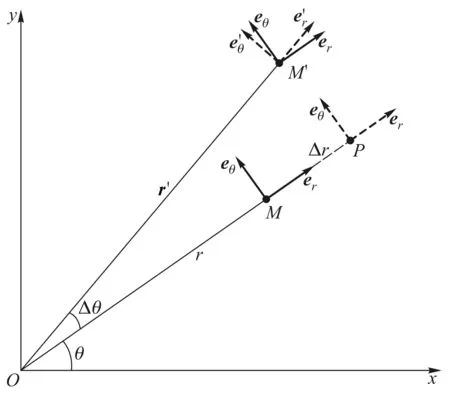
图1 极坐标系下单位矢量的变化

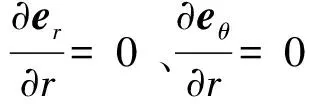
|Δer|≈|er|Δθ= Δθ

(2a)

|Δeθ|≈|eθ|Δθ= Δθ

(2b)

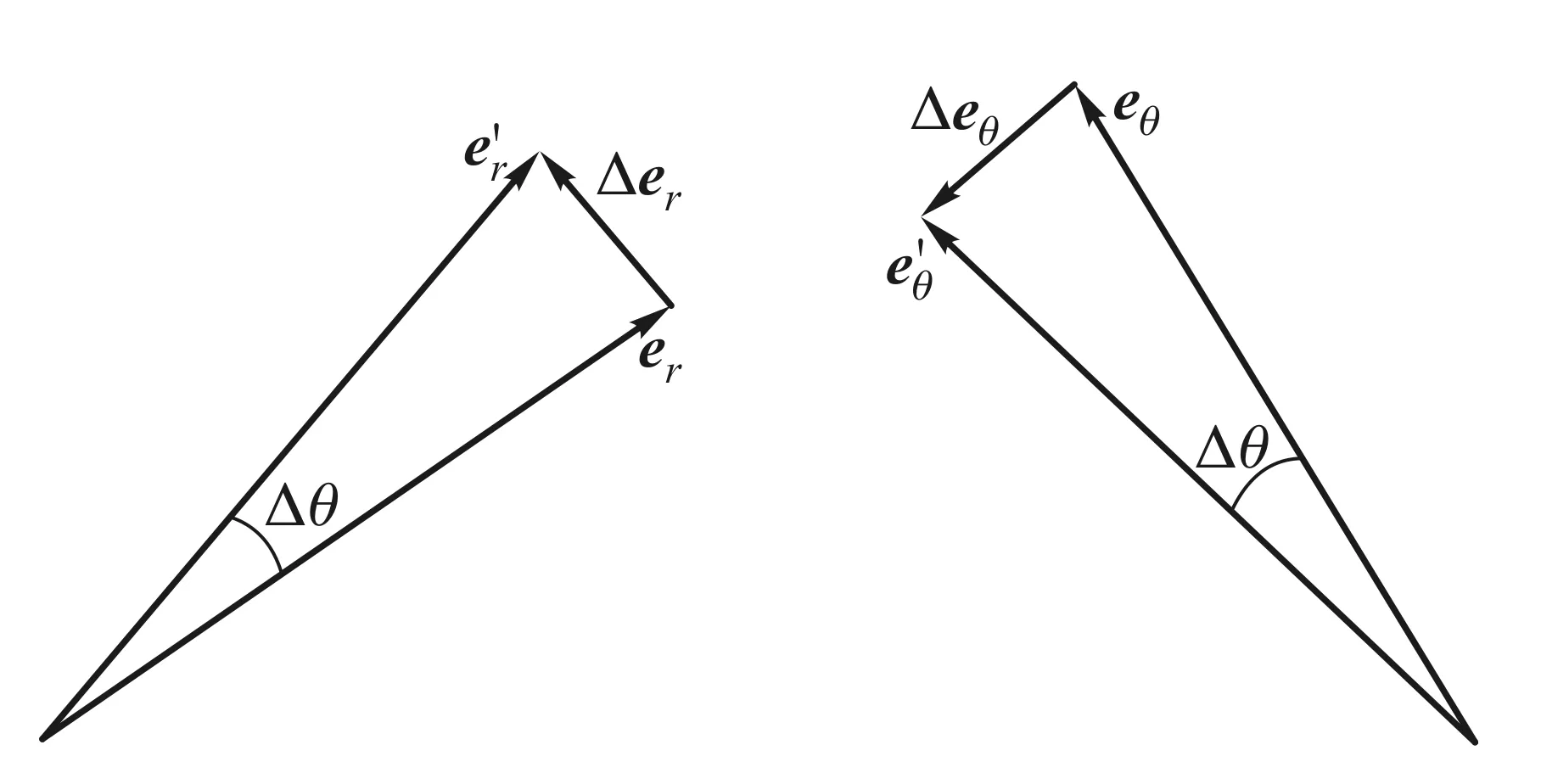
图2 Δθ→0时Δer和Δeθ方向的判断

将(2a)、(2b)分别代入(1b)、(1d)，取极限Δθ→0得到：

(3a)

(3b)

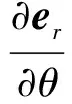
(4a)

(4b)

将上述方程整理后得到极坐标系下单位矢量的空间导数为：

(5a)

(5b)

2 柱坐标系下单位矢量的空间导数

柱坐标系是在xy面的极坐标系(ρ，φ)基础上增加了与之垂直的z轴坐标，如图3所示.根据第1节关于极坐标单位矢量的偏导数的计算，可以首先确定由坐标(ρ，φ)构成的极坐标系下的单位矢量偏导数：

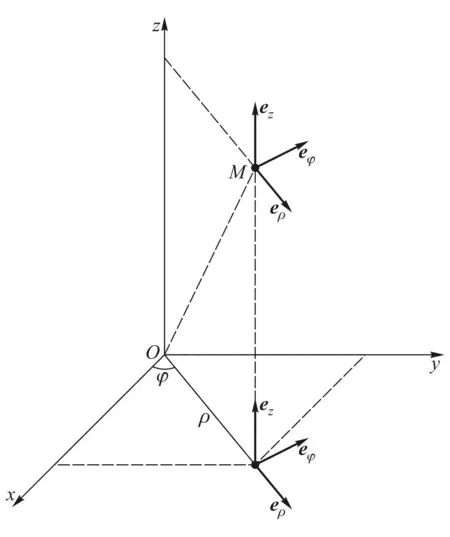
图3 柱坐标系及其单位矢量

(6)

因为z坐标方向固定，其单位矢量ez为常矢量，所以与其相关的坐标偏导数为零：

(7)

当z增加Δz时，根据矢量平移原则，eρ、eφ大小及方向不变，所以eρ、eφ与z坐标相关的导数为零：

(8)

将上述方程整理后，得到柱坐标系下单位矢量的空间导数为：

(9a)

(9b)

(9c)

3 球坐标系下单位矢量的空间导数

球坐标系如图4所示，任意点坐标用(r，θ，φ)表示，相应的单位矢量为er、eθ、eφ.由图可见，er、eθ均在ρ、z所构成的平面内，r、θ构成平面极坐标系，根据第1节讨论，可以得到：

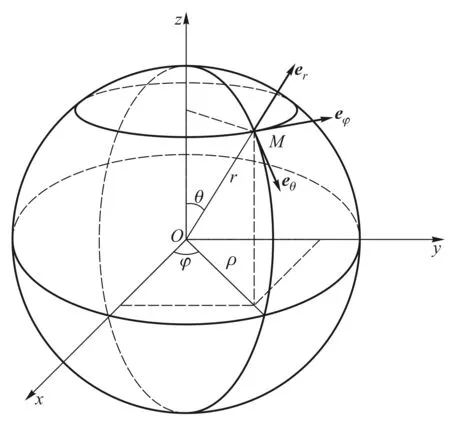
图4 球坐标系及其单位矢量

(10)

eφ的方向垂直于ρz平面，沿着φ增加的方向，所以，eφ的大小及方向不随r或θ的变化而变化，则

(11)

在r、θ不变的情况下，当φ增大Δφ时，er、eθ、eφ均随之旋转，相关单位矢量也会随之变化.er、eθ可分解为ρ和z两个方向的分量，其中与z轴平行的分量不发生变化，但在xy平面内沿ρ轴方向的投影会有方向变化，eφ方向平行于xy平面.可以确定，Δer、Δeθ、Δeφ均在经过M点与z轴垂直的纬线平面内，如图4所示. 根据矢量的平移不变性，该面可以看作由ρ和φ构成的极坐标平面.令|er|ρ和|eθ|ρ分别为er、eθ在ρ轴上投影的大小，根据矢量的单位圆关系(如图5所示)，可以得到：

|er|ρ=|er|sinθ， |eθ|ρ=|eθ|cosθ

(12)

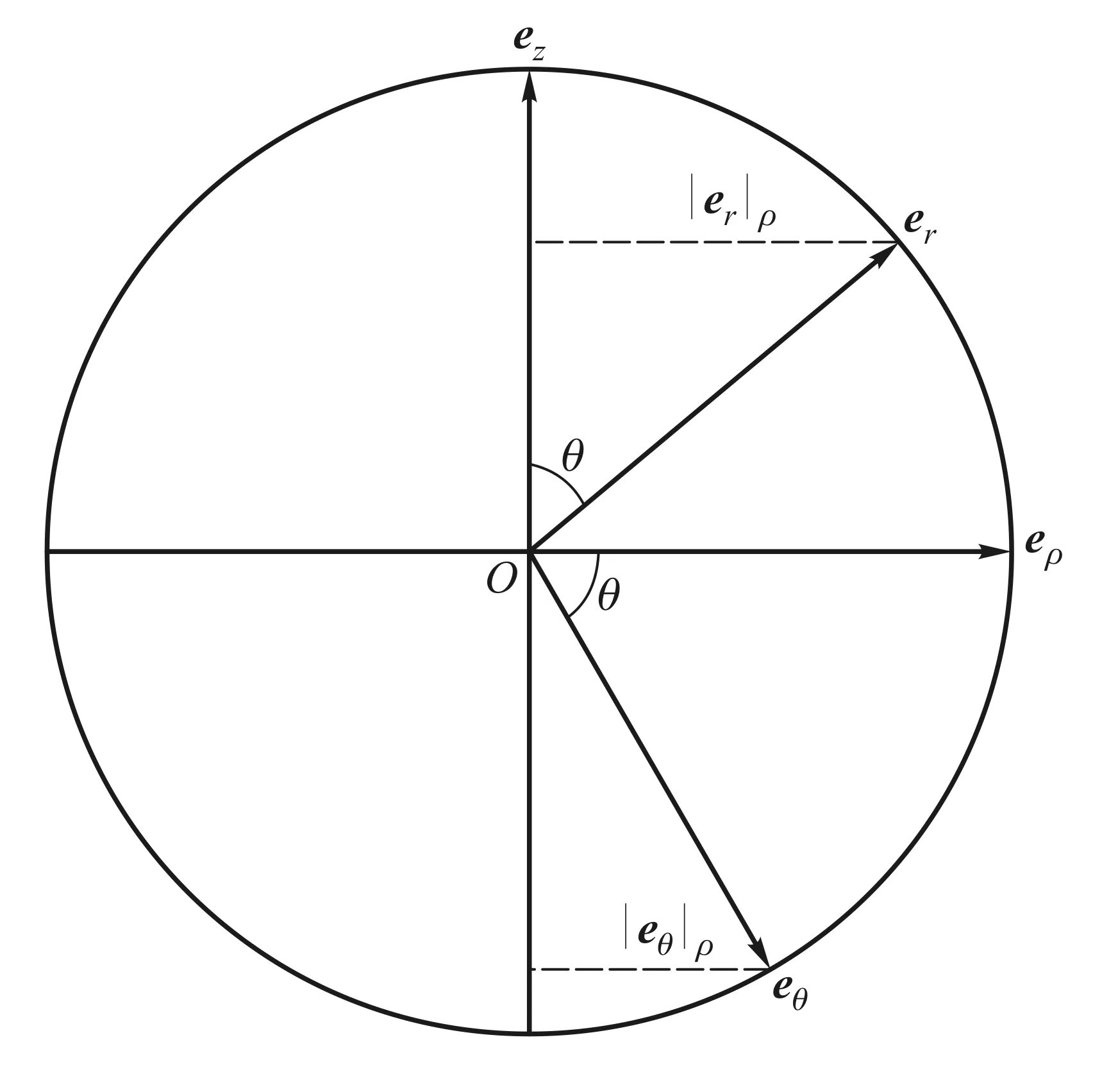
图5 单位矢量的单位圆

|er|ρ和|eθ|ρ亦可看作位于ρ、φ构成的与z轴垂直的纬线平面内的极坐标系中.根据第1节推导可知，当Δφ很小时有

|Δer|ρ≈|er|ρΔφ= sinθΔφ，

|Δeθ|ρ≈|eθ|ρΔφ= cosθΔφ

(13)

由于er、eθ在z轴的分量不发生变化，所以|Δer|=|Δer|ρ，|Δeθ|=|Δeθ|ρ，方向沿eφ方向，Δφ→0取极限得：

(14)

同理，在r、θ不变的情况下，当φ增大Δφ时，则

(15)

根据图5单位圆表述的矢量关系：eρ=ersinθ+eθcosθ，可得

(16)

将上述方程整理后，得到球坐标系下单位矢量的空间导数为：

(17a)

(17b)

(17c)

4 结论

利用微分几何和矢量极限的方法求解了单位矢量的空间导数，过程基于微分几何原理及曲线坐标系间的空间关联，简洁明晰. 根据全微分的定义，再配合单位矢量的空间导数，很方便地得到常见曲线坐标系下单位矢量对时间的导数以及运动学变量位矢、速度、加速度，便于加深对概念的理解，也适合在课堂教学中使用.

[1] 顾樵. 数学物理方法[M]. 北京: 科学出版社， 2012:15-19.

[2] 林为干， 符果行， 邬琳若,等. 电磁场理论[M]. 北京: 人民邮电出版社， 1984: 183-187.

[3] 徐重光， 朱菊香. 广义矩阵法在求任意曲线坐标系的导热方程的应用[J]. 松辽学刊(自然科学版)， 1991，3: 1-7.

[4] Koo W K， Liew Y C. 正交曲线坐标系中单位矢量的时间导数[J]. 大学物理， 1992， 11(4): 46-47.

[5] 成泰民， 孙树生. 正交曲线坐标系中单位基矢的导数[J]. 大学物理， 2010， 29(6): 27-29.

[6] 安秉权，杨焕雄. 求一般正交曲线坐标系中单位基矢之时空导数的一种简便方法[J]. 固原师专学报(自然科学)， 1998， 19(3): 32-34.

[7] 周衍柏. 理论力学教程[M].3版. 北京: 高等教育出版社， 2009: 8 -11.

[8] 邵毅全， 田莉兰， 黄永超,等. 极坐标下矢量的微分几何研究[J]. 激光杂志， 2015， 36(1): 85-86.

The solution of spatial derivatives of unit vectors using differential geometry method

LUO Hong-chao, JU Li-ping

(School of Science, Shenyang Aerospace University, Shenyang, Liaoning 110136, China)

By using the differential geometry, the vector limit and the relationship of various coordinate systems, we deduce the spatial derivatives of unit vectors in common curvilinear coordinates. This derivation method is simple and intuitive, which is easy to understand and apply in physics teaching and practice.

unit vectors; differential geometry; curvilinear coordinate; spatial derivative

2016-03-10；

2016-06-04

辽宁省普通高等教育本科教学改革研究项目(UPRP20140282)、沈阳航空航天大学本科教学改革研究项目(2014年)资助

罗宏超(1978—)， 男， 辽宁阜新人，沈阳航空航天大学理学院讲师，硕士，主要从事基础物理教学及原子分子物理研究工作.

O 411

A

1000- 0712(2016)12- 0023- 03