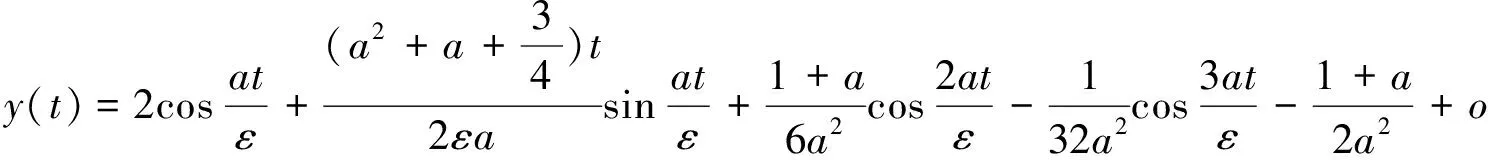一类具零频率的Nagumo型方程的同伦摄动近似解
余梦兰 韦玉程
(河池学院 数学与统计学院, 广西 宜州 546300)
一类具零频率的Nagumo型方程的同伦摄动近似解
余梦兰 韦玉程
(河池学院 数学与统计学院, 广西 宜州 546300)
考虑由典型的发放神经元模型—FHN模型简化得到的Nagumo方程,应用同伦摄动理论,通过引入一嵌入变量p∈[0,1]构造一同伦函数,求解得方程的一阶近似解和参数a的估计值。
同伦摄动方法;Nagumo方程;近似解
0 引言
在科学和工程研究中特别是在现代科学技术中出现的非线性问题是极为常见的。解决科学、工程、科技中的问题很大程度上归结为解非线性方程的问题。然而,绝大部分非线性问题无法获得精确的解析解,因此求解非线性方程的近似解具有非常重要的实际意义。随着现代科学技术的不断发展,学者们提出了很多种求非线性方程近似解的方法,如迭代法、变分法、摄动方法、同伦分析法、同伦摄动法等等[1-2]。
摄动方法是求解非线性问题的常用方法之一,但各种摄动方法都有一定的局限性。首先,摄动方法应用对象为含有小参数的方程,限制了其本身的应用范围;第二,各阶摄动方程与原始非线性方程密切相关;第三,摄动级数的收敛性强烈依赖小参数。为解决这些问题,数学工作者引入了 Lyapunov 人工参数法、δ展开法、Adomian 分解法等不需要小参数的方法[3-5],但级数解的收敛性问题没有办法保证,也不能自由选择表达非线性方程解的基函数。基于此,1992年廖世俊根据拓扑理论中的同伦概念提出了一种新的解决非线性问题的方法——同伦分析方法,并于1997年进一步引入“收敛控制参数”将同伦分析法加以完善[6-7]。1998年何吉欢结合同伦分析法与摄动法的相关理论提出了同伦摄动方法,其基本思想如下[8-9]。
考虑非线性方程:
A(u(t))=L(u(t))+N(u(t))=0,
其中L,N分别为A的线性部分与非线性部分。构造同伦
H(p,u)=(1-p)[L(u)-L(u0)]+pA(u)=0,
其中p∈[0,1]为嵌入参数。对于不同的参数p对应的方程不同,其解也不相同。令u=u(t,p), 即
H(p,u)=(1-p)[L(u(t,p))-L(u0)]+pA(u(t,p))=0,
当p=0时,L(u(t,0)-u0)=0 ;当p=1时,A(u(t,1))=0.于是,此同伦是将线性方程的解u0连续地变到了非线性方程A(u)=0的解。将嵌入参数p视为小参数, 将u展开为p的幂级数

当p=1时, 得到
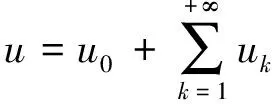
就是非线性方程A(u)=0的解。
同伦摄动法的主要特点是,克服传统摄动理论对小参数的过分依赖问题,特别是对非线性问题的控制和边界条件不管是否含有小参数,都能将其自由边界问题转化为固定边界问题;而且,该方法可以自由选取最适合问题的基函数,更有效的取得问题的解;除此之外,同伦摄动方法提供的简洁有效途径使得到的级数解收敛,获得精确的近似解。近年来,同伦摄动法成功的应用到许多涉及非线性问题领域的求解之中。
生命科学的研究表明:发放型神经元在神经网络中的研究极为重要[10-11]。时下,以发放型神经元模型为基础构成的联想记忆神经网络模型是国际上生物数学研究的热点。FitzHugh-Nagumo方程(简称FHN方程)是发放型神经元的数学描述,其形如下:
ut=uxx+u(u-α)(1-u)-β∫udt,(0<α<1,β>0)
参数α是由细胞膜的电特性决定的参数。由于非线性FHN方程的复杂性,缺乏一种求出FHN方程解析解的方法,因此在对FHN模型进行研究时学者们常借助于数值方法。当FHN方程中参数β=0时,即得到 Nagumo方程:
ut=uxx+u(u-α)(1-u),
对于Nagumo方程,人们感兴趣的是寻找形如
u(x,t)=q(ξ),ξ=kx-ωt+ξ0,
的行波解,其中k>0为波数,ω为角频率,ξ0为常数。则q满足方程
k2q″+ωq′+q(q-α)(1-q)=0.
此方程可化为Lienard方程,它具有三个平衡点q=0;α;1,而且都是双曲型。对于Nagumo方程的研究,可参见Iqbal[12]及Mckean[13]及其参考文献。受其启发,我们运用同伦摄动方法考虑具有零频率的Nagumo方程为背景的一类二阶微分方程的近似解问题。
1 主要结果及其证明
定理:考虑形如
ε2y″+y(1-y)(y-a)=0,
(1)
一类具有零频率的简化Nagumo型方程,其中ε为小参数,y(0)=1,0 这里a≈0.793 054,t为变量,o(t)是误差项。 注:方程(1)有三个奇点y=0;y=a;y=1,取定初始值y(0)=1,是指以奇点(0,1)为出发点。 定理的证明: 对于方程(1), 我们选择构造下面的同伦,y(t)→y(t;p): (1-p)[ε2y″(t;p)+a2y(t;p)]+p[ε2y″(t;p)+y(t;p)(1-y(t;p))(y(t;p)-a)]=0, 即 ε2y″(t;p)+(1-p)a2y(t;p)+p[(1+a)y2(t;p)-ay(t;p)-y3(t;p)]=0,p∈[0,1] (2) 这里p为嵌入参数,y(0)=1为方程(2)的初始解。 当p=0 时,方程(2)转化为一个线性方程: ε2y″(t;p)+a2y(t;p)=0, 当p=1 时,方程(2)就是原来的非线性方程(1)。应用摄动理论[12-13],我们假设(2)的解可表示为 y(t;p)=y0(t;p)+py1(t;p)+p2y2(t;p)+…, (3) 当ρ→1,方程(2)转化为方程(1),这时(3)式变成了方程(1)的近似解,即 把(3)代入(2),得: ε2(y0(t;p)+py1(t;p)+p2y2(t;p)+…)″+(1-p)a2(yo(t;p)+py1(t;p)+p2y2(t;p)+…)+p[(1+a)(y0(t;p)+py1(t;p)+p2y2(t;p)+…)2-a(yo(t;p)+py1(t;p)+p2y2(t;p)+…)-(y0(t;p)+py1(t;p)+p2y2(t;p)+…)3]=0. 即有 ε2y″0(t;p)+ε2py″1(t;p)+…+a2y0(t;p)+pa2y1(t;p)+…-pa2y0(t;p)- 比较p的相同次幂系数,得: p0: ε2y″0(t;p)+a2y0(t;p)=0; (4) p1: (5) 解方程(4),得其通解为: 由于y(0)=1, 于是,我们可选取如下的基函数 (6) 把(6)代入(5)并化简得: (7) 下面我们通过方程(7)解出y1的具体表达式。 首先考虑其对应的齐次方程 ε2y″1(t;p)+a2y1(t;p)=0 类似于方程(4),我们选定基函数为 其次我们将非齐次线性方程(7)折分成下面四个非齐次线性方程: 分别求出这四个非齐次线性方程的一个特解: 根据常微分方程解的叠加原理,方程(7)的解可表示为: 于是可得方程(1)的一阶近似 y(t)=y0(t;p)+y1(t;p)+o(t) (8) 由初值y(0)=1知,当t=0时有: 把t=0代入(8)式,可得到 即 96a2-32a-35=0, 解这个方程,并注意到0 至此,我们得到了所需要的结果。定理证明结束。 [1] Nayfeh A H. Perturbation methods[M].New York: John Wiley & Sons, 2000. [2] Smith D R. Singular-perturbation theory[M]. London: Cambridge University Press, 1985. [3] Lyapunov A M. General problem on stability of motion[M]. London:Taylor & Francis, 1992. [4] Awrejcewicz J, Andrianov I V, Manevitch L I. Asymptotic approaches in nonlinear dynamics[M]. Berlin: Springer Verlay, 1998. [5] Adomian G. Nonlinear stochastic differential equations [J]. Math Anal and Applic., 1976, 55: 441-452. [6] 廖世俊.同伦分析方法:一种不依赖于小参数的非线性分析方法[J].上海力学, 1997,8(3):197-200. [7] 廖世俊.超越摄动:同伦分析方法基本思想及其应用[J].力学进展, 2008, 38(1): 1-34. [8] He J H., An approximate solution technique depending upon an artificial parameter[J]. Commun Nonlinear Sci Numer Simulat, 1998, 3(2):92-97. [9] He J H. Homotopy perturbation techique[J]. Comput. Methods Appl. Mech. Engrg., 1999, 178:257-262. [10] Fitzhugh R. Impulses and Physiological State in Theoretical Models of Nerve Membrane[J]. Biophys, 1961, 1: 445-467. [11] 张伟,乔清理.联想记忆人工神经网络的发展和研究现状[J].医疗卫生装备, 2008, 29(5):36-38. [12] Iqbal M. Numerical Solutions of Nagumo’s Equation [J]. Journal of Applied Mathematics & Decision Sciences, 1999, 3(2): 189-193. [13] Mckean H P. Nagumo’s Equation [J]. Advances in Mathematics, 1970, 4: 209-223. [责任编辑 刘景平] The Homotopy Perturbation Approximation Solution of A Class of Nagumo Equations with Zero Frequency YU Menglan, WEI Yucheng (School of Mathematics and Statistics, Hechi University, Yizhou, Guangxi 546300, China) In this paper, we considered a class of two order nonlinear equations by simplifying the classical neuron model—FHN equation. Using the homotopy perturbation method what completely does not depend on small parameters, we get the first order approximate solutions for it and estimate value of parameteraby introducing a embedded variablep∈[0,1], constructing a homotopy function and using the perturbation theory. homotopy perturbation method; Nagumo equation; approximate solution O175.12 A 1672-9021(2016)05-0064-05 余梦兰(1992-),女,广西天峨人,河池学院2011级学生;韦玉程(1966-),男,广西凤山人,博士, 河池学院数学与统计学院副教授, 主要研究方向:变分法。 广西教育厅自然科学研究基金资助项目(KY2015YB255); 广西教育厅教改基金资助项目(2015JGA322;2015JGB355)。 2016-02-25