海上浮式风机运动响应的时域耦合计算方法

金飞，滕斌

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

海上浮式风机运动响应的时域耦合计算方法

金飞，滕斌

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

建立了一种用于计算海上浮式风机运动响应的时域耦合方法，该算法主要由气动力模块、水动力模块、系泊模块和系统运动模块构成。气动力模块采用叶素动量法；水动力模块采用一阶势流理论，通过边界元法求解；系泊模块采用悬链线模型，用Chebyshev多项式进行拟合计算。对于系统运动模块，采用Runge-Kutta法求解。对OC3-Hywind spar风机进行了建模，对各模块及耦合模型的进行对比研究，验证了此耦合计算方法的准确性。并利用该方法计算和分析了此风机的运动响应及其对风机功率的影响。

浮式风机；时域耦合方法；叶素动量法；边界元法；悬链线模型

风力发电作为一种利用可再生、清洁能源的技术，已经得到国内外广泛研究和使用[1]。目前风机的主要形式可分为陆上风机和海上风机2种。而海上风机又可以分为海上固定式和海上浮式风机。相比于陆上风机，海上风机摆脱了土地利用以及风场大小的限制[2]。而由于近岸区域海岸线利用的限制，海上风机将逐渐走向深水区域，此时海上固定式风机的建造费用将剧增，不利于经济效益。海上浮式风机的概念应运而生，它能适应深水环境，具有发电稳定、风能利用率高等优势，具有广阔的应用前景。

海上浮式风机由风机、浮体平台、锚链等多部分组成，受到风场、波浪、潮流等共同作用，受力非常复杂，在运动过程中可能出现失稳、倾覆等问题，所以需要对系统作整体的耦合分析。耦合分析可以充分考虑结构各部分以及各力之间的相互影响，在计算结构运动、动力响应等方面能得到更准确的结果。Withee（2004年）[3]使用FAST和ADAMS开发了全耦合动力响应程序，用来计算浮式风机在风场和波浪作用下的响应。该程序同时考虑了浮体受到的非线性波浪荷载和风机受到的空气动力荷载。Nielsen（2006年）[4]使用空气动力学程序HAWC2和计算海洋结构物动力响应的程序SIMO/RIFLEX，开发了计算浮式风机在风场、波浪作用下动力响应的程序。唐耀（2013年）[5]对Spar型浮式风机平台做了耦合动力响应分析。对于风力荷载，采用Knauer等提出的经验公式进行简化计算。对于水动力计算，使用SESAM软件中的DeepC模块计算系泊状态下浮式风机系统的运动响应及锚链的张力。

以往在进行时域内浮式风机水动力计算时常采用频域转时域的方法，如商业软件SESAM中的一些计算模块就采用这样的方法。虽然此种方法计算速度快，但是需要先求出高频下结构物的水动力系数，这对于复杂结构物是比较困难的。另外，频域理论中通常假设浮体的运动幅度较小，而浮式风机由于受到风的作用，水平方向的漂移较大，这时此种方法将带来误差。针对这个问题，本文采用直接时域方法进行浮体水动力计算。这种方法对有限振幅运动的时域计算将更加准确和有效，同时也可以与气动力计算和系泊计算方便地进行耦合。这样建立的耦合计算方法将更真实地刻画时域内海上浮式风机的运动响应。

1 耦合计算方法

本文将建立一种用于计算海上浮式风机运动响应的时域耦合方法，并形成一套完整而独立的时域耦合计算程序。对于风机所受的气动力荷载，采用经典的叶素动量法计算。对于浮体平台的水动力荷载，在一阶势流理论下采用边界元法进行计算。对于锚链模型，采用Chebyshev多项式拟合的悬链线模型计算。对于系统运动模块，采用Runge-Kutta法求解。

1.1 风机气动力理论

本文采用叶素动量法（blade element momentum method）进行风机气动力计算[6]。叶素动量法由动量理论和叶素理论构成。

根据动量理论，风机平面dr圆环上的轴向力可以表示为：

式中：v1为来流风速；r为圆环至圆心距离；ρ为空气密度；a为轴向诱导因子。环形单元的扭矩为：

式中：ω为风机旋转的角速度；a′为切向诱导因子。

根据叶素理论，将叶片分为若干个叶素段，每一段内采用一种翼型数据。对于给定的叶素段，通过推导，风机平面dr圆环上的轴向力和扭矩可以表示为：

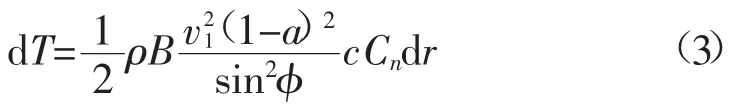
式中：B为叶片数；φ为相对来流风速与风机平面的夹角；c为此翼型的弦长；Cn为垂向分力系数。

让式（1）与式（3）相等、式（2）与式（4）相等，即有：

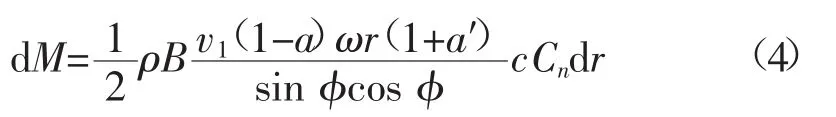
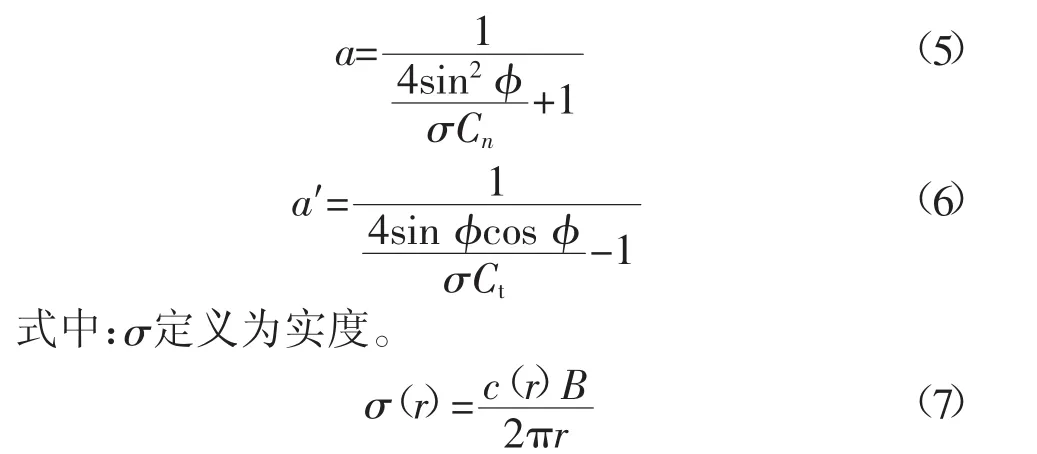
具体计算时，不断迭代轴向和切向诱导因子直至收敛，即可计算出dr圆环上的轴向力和扭矩，积分后即可得到整个风机的受力。

以上即为叶素动量法，为了获得更精确的结果，这里进行了两项修正。第一项为Prandtl叶尖损失修正。第二项为Glauert修正。

浮式风机在波浪的作用下将产生纵荡、纵摇等运动形式，此时风机平面将发生变化，导致相对来流风速vrel和入流角度φ的改变，从而引起风机轴向力和功率的变化。而浮式风机在运动过程中还具有速度，也会导致相对来流风速的变化。比如当浮式风机发生纵摇时，风机平面发生偏转，首先导致入流角度发生变化，这时垂直于风机平面的来流风速分量也将发生变化，因此迭代计算结果也会改变，即轴向和切向诱导因子会改变，最终风机轴向力和功率发生变化。因此计算浮式风机气动力时需要考虑系统的位移和速度。

1.2 波浪与浮体作用的时域分析方法

由于浮式风机一般布置在深水区，其截面尺度相对于波浪要素基本上是小尺度，因此采用势流理论计算一阶波浪力就可以较准确地计算出其受力[7]。

一阶势流理论下速度势函数Φ和波面函数η可以分为已知的入射分量和未知的散射分量：

式中：散射势ΦS包含所有由于波浪和物体扰动而产生的散射分量。

散射势在域内满足Laplace方程：

并满足如下边界条件:

式中：n为物面的法线方向，规定指出物体为正。

为了构成定解问题，还需增加一个远场辐射边界条件。在数值计算中，采用增加人工阻尼层来保证散射波向外传播而不反射回来。

利用简单格林函数法，选取Rankine源和它关于海底的像作为格林函数：

式中：x为场点；ξ为源点。利用格林第二定律，可以得到关于计算域边界上散射势的边界积分方程：

式中：边界S包括淹没在水中的物体平均湿表面SB和从物体到阻尼层外边界的有限静水面SF；α为固角系数。

根据散射势的自由水面条件式（11）、式（12），采用高阶边界元法求解边界积分方程即可计算出速度势。得到速度势后，就可以计算出物面的压强及受力。对于线性波浪，作用在物体上的一阶波浪力可以表示为：

1.3 锚链模型

对于海洋中的浮体结构，需要锚链对其进行定位和约束。进行锚链力的计算时，常采用悬链线模型。具体计算时，常采用分段外推-校正法计算，即首先对锚链分段，对每一段求解，然后外推，经过多次迭代校正后得到最终的结果。

但在时域内的浮体—锚链系统中，每个时间步上浮体的位置都在变化，因此迭代的计算量会显著增加。针对这个问题，本文采用Chebyshev多项式对锚链顶端位置和顶端拉力函数进行拟合，求出用于计算锚链顶端位移与受力关系的拟合公式[8]。

应用Chebyshev多项式进行拟合能够根据锚链的顶端位置，方便、快速地求出锚链顶端的拉力，能够应用在浮体—锚链系统的耦合计算中。

1.4 时域耦合模[10]

海上浮式风机的运动受到波浪力、锚链力、风机轴向力的相互耦合作用。对于一个给定的系统状态（已知浮式风机的位移和速度），可以计算出此时各部分的外力。系统受到这些外力的作用，下一时刻的状态就会改变。而波浪与结构物、锚链与浮体、风与浮式风机各自都存在相互作用，而各部分间又有相互作用，因此使得整个问题成为一个非常复杂的耦合问题。

本文在耦合计算时采用的思路可以由图1体现。系统运动模块将系统的位移、速度传递给对应的计算模块，各模块计算后将力、力矩返回给运动方程，周而复始完成时域计算。图1中的风机参数包括风机模型尺寸、叶片气动力特性等参数，波浪参数包括波高、周期或者波浪谱的参数，锚链参数包括锚链强度、长度、类型等参数。

图1 耦合计算流程图Fig.1 Flow chart of the coupled calculation

对于气动力模块，系统运动模块将为其提供浮体的位移和运动速度，根据给定的风机参数计算出当前时刻的风机轴向力和力矩；对于水动力模块，系统运动模块也将为其提供浮体的位移和运动速度，根据给定的波浪参数计算出当前时刻的水动力和力矩；对于系泊模块，系统运动模块只需为其提供浮体的位移，因为在锚链力的计算中，不涉及浮体的运动速度，根据给定的锚链参数计算出当前时刻的锚链力和力矩。这些力和力矩将返回到运动模块中，根据运动方程计算出下一时刻的位移和速度。系统运动模块分别与其余3个模块有变量交换，完成了相互之间的耦合作用，因此这样的模型是在时域上全部耦合的，能够充分考虑各部分外力与整体系统的相互作用。

系统运动模块中的运动方程可以表述为：

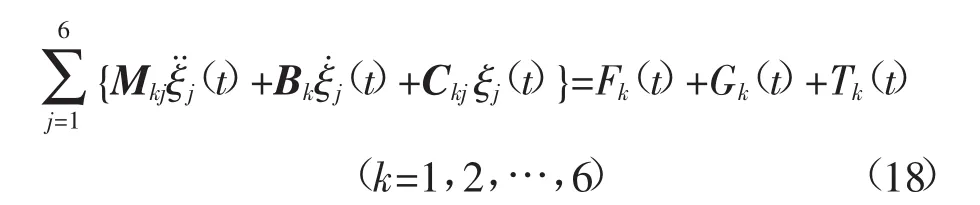
式中：Fk为总的广义水动力荷载分量（包括力和力矩）；Gk为锚链作用力和力矩；Tk为风机轴向力和力矩。对于以上3个参数，k=1～3时分别表示x，y，z方向的力；k=4～6时分别表示对x，y，z轴的力矩。Mkj为物体的质量矩阵；Bk为系统阻尼矩阵；Ckj为恢复力矩阵。

具体数值求解时，把式（18）的二阶微分方程写成如下的通用格式：

采用四阶Runge-Kutta法求解此二阶微分方程，计算时首先根据t时刻物体的位移ξ（t）和速度ξ˙（t），由水动力模块确定波浪激振力、恢复力和阻尼力，由系泊模块确定锚链力，由气动力模块确定风机轴向力，从而求得t时刻函数，再由Runge-Kutta法计算出t+Δt时刻新的位移ξ（t）和速度。重复该过程直至计算结束。

2 模型建立与验证

计算模型采用的是2010年Jonkman提出的OC3-Hywind spar型海上浮式风机[11]。上部风机为NREL 5-MW风机。浮体部分为spar型圆柱结构。采用3根对称分布的锚链进行系泊。部分重要参数见表1—表2，锚链布置形式见图2。

表1 风机与塔架参数Tab.1 Parameters of the wind turbine and tower

2.1 气动力验证

利用1.1中的气动力理论编写程序，对于不同风速下的固定式风机进行计算（不考虑风机实际的控制策略），并与其他程序和结果进行了对比验证。

2.1.1 功率验证

利用Blade Element Method计算不同风速下、风机固定时的功率，并与FAST程序结果进行比较，对比结果如图3所示。

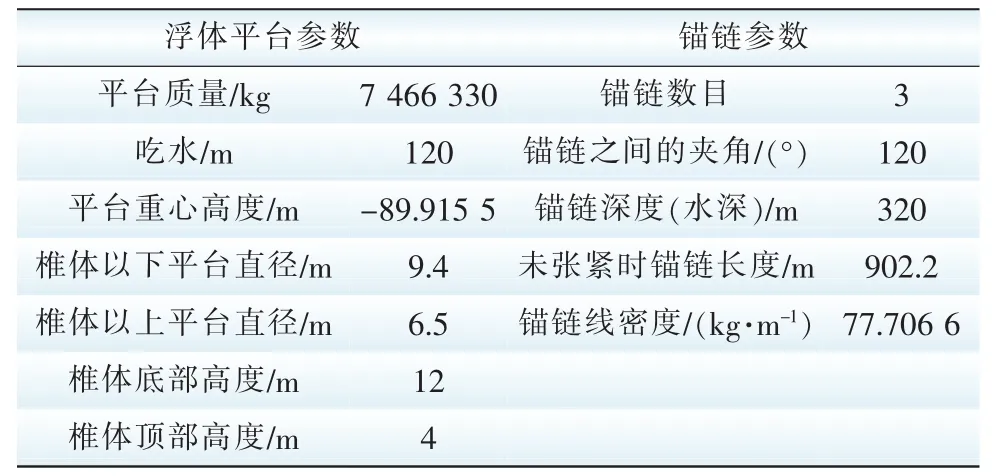
表2 浮体平台与锚链参数Tab.2 Parameters of the platform and anchor chain

图2 锚链布置形式Fig.2 Layout of the anchor chains

图3 不同风速下固定式风机功率Fig.3 Powers of the fixed wind turbine in different wind velocities

对比显示，在风速7～14 m/s时，程序计算结果与FAST结果基本吻合，当风速较大时，存在一定误差。

2.1.2 推力验证

11.4 m/s是该风机的额定风速，需要对此风速下风机受到的推力重点验证。这里计算了该风速及其附近风速下风机受到的推力，并与文献结果进行了比较，结果如表3所示。

对比显示，额定风速及其附近风速下风机受到的推力（即轴向力）与文献结果吻合。

综合以上2个验证，表明风机参数设置正确，气动力模块计算结果准确。

表3 风机推力结果Tab.3 Results of the axial force of the wind turbine

2.2 水动力验证

利用1.2和1.3中的理论和模型，对浮式风机系统进行水动力计算。考虑入射波为规则波，波高2.56 m，周期10 s，入射方向朝向x正方向。锚链采用悬链线模型。此时不考虑风的作用。由于浮体平台和锚链布置的对称特性，当来浪方向平行于x轴时，其运动响应只有在纵荡、垂荡、纵摇方向上有值，其余3个方向上为0。图4—图6是浮体纵荡、垂荡、纵摇的计算结果。

图4 浮体纵荡历程及其幅值谱Fig.4 The history and the amplitude spectrum of surge of the floating platform

从运动响应可以看出，经过一段时间后，浮体在平衡位置附近做规则的往复运动。从谱分析的结果也可以看出，谱峰频率是入射规则波的频率，说明浮体主要受波浪的影响。为了验证水动力计算的准确性，将稳定后的运动响应幅值与时域下锚链采用等效刚度以及频域下锚链采用等效刚度的结果进行了比较，如表4所示。

图5 浮体垂荡历程及其幅值谱Fig.5 The history and the amplitude spectrum of heave of the floating platform

图6 浮体纵摇历程及其幅值谱Fig.6 The history and the amplitude spectrum of pitch of the floating platform

从上述比较结果中可以看出，采用悬链线的时域计算结果与其他2种方法非常吻合，说明浮体模型参数设置准确，水动力模块计算准确。

表4 浮式风机运动响应幅值比较Tab.4 Comparison among amplitudes of the motion response of the floating wind turbine

2.3 耦合计算验证

浮式风机受到风、波浪、锚链的耦合作用，除了需要对每个模块验证准确性，还需对整体耦合计算模型进行准确性验证。为了与已有的计算结果进行比较，本文进行了浮式风机平衡位置的计算，以此作为耦合模型的验证。

风速为11.4 m/s，朝向x正方向。入射波波幅为0（存在辐射波，仍考虑水动力模块），锚链采用悬链线模型。其纵荡计算结果如图7所示。

图7 浮式风机纵荡历程Fig.7 The history of surge of the floating wind turbine

从图7中可以看出，经过一段时间后，纵荡达到了稳定，平衡在27.8 m。文献[5]中给出的结果为25.7 m。考虑到所用的计算模型存在误差，计算结果还是比较吻合的。平衡位置的耦合计算虽然没有计入入射波的作用，但是依然考虑了水动力模块，浮体的运动会产生辐射波浪力，也与气动力形成了相互作用。因此，仍然是气动力模块、水动力模块、系泊模块的相互耦合计算。上述验证说明整体系统模型参数设置准确，各部分模块及耦合程序计算准确。

3 结果分析

3.1 规则波计算

入射波为规则波，波高2.56 m，周期10 s，入射方向朝向x正方向。锚链采用悬链线模型。风速11.4 m/s，朝向x正方向。图8给出了2种计算中纵荡结果的比较。其中wave-induced指的是只考虑水动力作用，不计入气动力影响。wind-wave指的是气动力和水动力的联合作用。

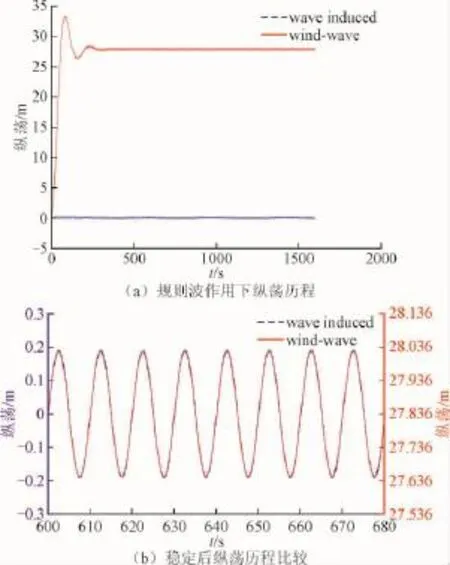
图8 规则波作用下浮式风机纵荡历程Fig.8 The history of surge with the regular wave of the floating wind turbine

从图8（a）、图8（b）中可以看出，在此计算条件下，气动力的作用主要是使系统在纵荡方向漂移了很长一段距离，稳定后，两者运动幅值与周期几乎一致，说明此时系统主要受到波浪的作用。表5中给出了3个方向上运动的具体数值。

表5 浮式风机运动的平衡位置与幅值Tab.5 Balance position and amplitude of motion of the floating wind turbine

3.2 运动响应对风机功率的影响

计算条件同3.1中的耦合计算一致，这里计算了浮式风机的功率，如图9所示。

由于初始效应，风机功率在0～300 s时有所波动，300 s后在一个平衡位置附近作周期性振荡。平衡后的平均功率为5 216 kW。而同样风速下，固定式风机的功率为5 363 kW。由此表明，由于浮体的运动，浮式风机的平均功率有所减小，减小约3%。

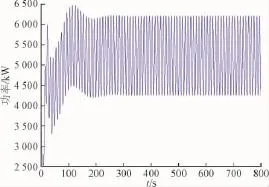
图9 风机功率历程Fig.9 The history of power of the wind turbine

4 结论

本文建立了一种用于计算时域内海上浮式风机运动响应的耦合方法，主要由气动力模块、水动力模块、系泊模块、系统运动模块构成。前3个模块通过与系统运动模块相互传递变量进行耦合计算。通过气动力验证、水动力验证以及耦合验证，表明各模块计算准确、各模块之间的耦合也是准确的。这样建立的时域内海上浮式风机运动响应的耦合计算方法是准确而有效的。此耦合计算方法计算速度快，准确性高，可以用于海上浮式风机的设计及研究。

本文计算了OC3-Hywind spar型海上浮式风机在11.4 m/s的定常风，波高2.56 m、周期10 s的规则波作用下的运动及其功率变化。初始阶段，浮式风机主要收到风机推力的影响，在纵荡方向会漂移很大一段距离，稳定值为27.8 m。稳定后，主要受波浪作用，在平衡位置处做往复运动。对于功率而言，由于浮体的运动，浮式风机的平均功率减小了约3%。

[1]张志春，刘洪伟.我国发展风电产业的战略性分析[J].电网与清洁能源，2013，29（5）:67-72.ZHANG Zhichun，LIU Hongwei.Strategic analysis of wind power industry development in China[J].Power System and Clean Energy，2013，29（5）:67-72（in Chinese）.

[2]郑小霞，叶聪杰，符杨.海上风电场运行维护的研究与发展[J].电网与清洁能源，2012，28（11）:90-94.ZHENG Xiaoxia，YE Congjie，FU Yang.Research and development of operation and maintenance for offshore wind farms[J].Power System and Clean Energy，2012，28（11）:90-94（in Chinese）.

[3]WITHEE J E.Fully coupled dynamic analysis of a floating wind turbine system[D].Monterey，California: Naval Postgraduate School，2004.

[4]NIELSEN F G，HANSON T D，SKAARE B.Integrated dynamic analysis of floating offshore wind turbines[C]//American Society of Mechanical Engineers.25th International Conference on Offshore Mechanics and Arctic Engineering，June 4-9，2006，Hamburg，Germany:ASME，2006:671-679.

[5]唐耀.Spar型浮式风机平台动力响应分析[D].上海:上海交通大学，2013.

[6]HANSEN M O L.Aerodynamics of wind turbines[J].Rotors Loads&Structure James，2015，5（2/3）:141-167.

[7]李玉成，滕斌.波浪对海上建筑物的作用[M].北京:海洋出版社，2002:95-98.

[8]滕斌，郝春玲，韩凌.Chebyshev多项式在锚链分析中的应用[J].中国工程科学，2005（1）:21-26.TENG Bin，HAO Chunling，HAN Ling.Numerical simulation of static behavior of the single anchor cable[J].Engineering Science，2005（1）:21-26（in Chinese）.

[9]SHIM S.Coupled dynamic analysis of floating offshore wind farms[D].Texas:Texas A&M University，2007.

[10]WAYMAN E N.Coupled dynamics and economic analysis of floating wind turbine systems[D].Massachusetts:Massachusetts Institute of Technology，2006.

[11]BUTTERFIELD S，MUSIAL W，SCOTT G.Definition of a 5-MW reference wind turbine for offshore system development[M].Golden，CO:National Renewable Energy Laboratory，2009:5-16.

[12]JONKMAN J M.Definition of the floating system for phase IV of OC3[M].Golden，CO:National Renewable Energy Laboratory，2010:2-21.

[13]马钰.单柱式浮式风机动力性能机理研究[D].上海:上海交通大学，2014.

（编辑 冯露）

A Coupled Time-Domain Calculation Method for Motion Response of Floating Offshore Wind Turbine

JIN Fei，TENG Bin
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，Liaoning，China）

In this paper，a coupled time-domain calculation method is established for the motion response of floating offshore wind turbine，mainly including aerodynamic，hydrodynamic，mooring and system motion modules.The blade element momentum method is used in the aerodynamic module and in the hydrodynamic module；the boundary element method is used for calculation under the first-order potential theory.In the mooring module，the catenary model is used with fitting calculation by the Chebyshevpolynomial.As for the motion module of the whole system，Runge-Kutta method is used to solve it.The OC3-Hywind spar wind turbine is modeled and the accuracy of this coupled calculation method is verified through the comparisons of each module and the coupled model.The method is used to calculate and analyze the motion response and its influence on the power of the wind turbine.

floating wind turbine；coupled time-domain method；blade element momentum method；boundary element method；catenary model

国家自然科学基金项目（51379032，51490672）。

Project Supported by National Natural Science Foundation of China（51379032，51490672）.

1674-3814（2016）08-0093-07

P751

A

2016-01-18。

金 飞（1991—），男，硕士研究生，研究方向主要为海上浮式风机的耦合计算。