基于序列光滑性分析的集抄数据缺陷判定

杨海涛，牟婷婷，杨海滔，辛洁晴

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海 200072；2.国网上海市电力公司市北供电公司，上海 200240）

基于序列光滑性分析的集抄数据缺陷判定

杨海涛1，2，牟婷婷1，杨海滔1，辛洁晴1

（1.上海交通大学电力传输与功率变换控制教育部重点实验室，上海 200072；2.国网上海市电力公司市北供电公司，上海 200240）

将集抄失灵后冻结电量的异常突增与正常的电量增长甄别开来是集抄缺陷分析的难点。为此，提出一种基于月累计电量序列光滑性分析的判定方法：通过光滑比分析搜索出疑似缺陷的数据序列；对这些序列进一步实施haar小波变换并求取Lipschitz指数，据累计电量序列异常突增表现为阶跃型突变、对应的Lipschitz指数接近于0的特点，辨别出异常突增缺陷。针对上海市北供电公司的算例结果表明，与现有经验性判据相比，所提方法对集抄电量异常突增缺陷具有更强的挖掘能力，可提高集中抄表环境下的出账准确率。

集中抄表；数据缺陷判定；光滑比；Lipschitz指数；小波分析

我国对低压用户已基本实现集中抄表全覆盖。不过，由于信道质量不佳、采集终端软件故障等原因，集抄数据常出现缺失或异常（冻结电量下降、异常高值等）[1-2]。因此，在集抄电量发布前须实施数据缺陷分析，对存在数据缺陷的用户进行核抄和消缺作业。由于集抄数据量巨大，建立合理的数据缺陷判定方法至关重要。

值得指出的是，目前供电公司的集抄消缺主要关注电量缺失问题。这种消缺能提升集抄在线率和采集率，对提升集抄数据准确率的作用非常有限。隐藏的异常数据很可能影响出账电量的准确性、进而激发供需矛盾或导致供电公司营销损失。因此，本文研究的集抄缺陷分析包括数据缺失和数据异常两方面的分析，并着重于后者的辨识方法。

相关文献中，绝大多数探讨的是集抄数据异常表象和对应的原因[1-2]，或是研究如何优化硬件设计方案[3]、优化消缺排查流程，以提高集抄成功率[4-5]。这些成果对消缺现场作业具有指导意义，但并没有回答如何在消缺作业前锁定待消缺用户的问题。

待消缺用户判定的现有研究成果较少，且多采用经验判据。文献[6]将集抄冻结电量异常归结为零值、空值、下降、异常突增几种，并着重对异常突增给出了“当日与前一日电量冻结值之差大于1 500或前日用电量小于10、当日用电量大于300”之经验判据；文献[7]则提出以用户装接容量的2～3倍（再综合用电时间）确定畸变判据。上述判据主观性强且过于严格，易漏判。

在其他领域，基于小波分析的信号奇异点检测已备受关注。例如：文献[8]对热力设备承压受热面检测信号实施小波分析，以诊断设备有无受到撞击、变形；文献[9]将小波变换应用于变压器负荷曲线和电压曲线奇异点分析，等等。通过小波变换的模极大值分析可找到信号奇异点（突变点），由奇异点的Lipschitz指数取值特点可进一步判定信号突变的类型（阶跃、斜坡、脉冲等等）。因不同领域信号异常突变的表象有所不同，将小波分析理论应用于集抄数据缺陷分析是一个值得专门研究的问题。

鉴于此，本文针对集抄所得的累计电量序列，提出一种基于光滑性分析的数据缺陷判定方法。该方法针对集抄点数量庞大的特点，首先据光滑比缩小疑似缺陷的序列范围；再对这些序列实施haar小波变换，据异常突增点（类似于阶跃型突变）与正常突增（斜坡型突变）Lipschitz指数的差异，将两类奇异点区分开来，以提高判定的准确性。

1 集抄数据特点分析

1.1 集抄正常数据表象

集抄系统采集的是低压用户每日0:00总电量和分费率电量的冻结值，这些冻结值构成的序列正常情况下呈如下特点。

1）连续：即不存在部分日数据缺失。

2）非降：冻结电量是用户日用电量的累计值，故非降。

3）多数情况下光滑：用户用电遵循一定规律，在气温不突变的情况下，日用电量也不会突变，故而冻结电量序列多数情况下是光滑的（以图1中序列1为例，图中数据为某年7月值且均标幺化、并转换为首值为零的基准下）；但在季节交替气温突变时、对某些气温敏感度高的用户而言（如图1中序列2），或是在用户用电行为突变时（如图1中序列3，该用户月中一段时间不用电），冻结电量序列也会呈现不平滑性。

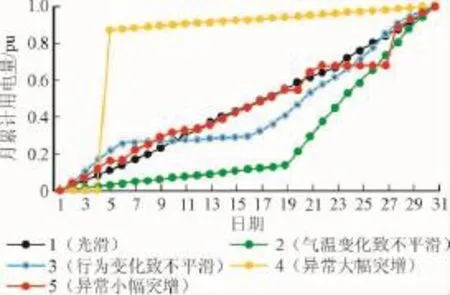
图1 集抄冻结电量序列的典型情况Fig.1 Typical freezing consumption series collected by the centralized metering system

4）总分电量匹配：指同一时刻采集的电量冻结值中，总电量冻结值与各分费率电量冻结值之和应相等。

1.2 集抄缺陷数据表象

数据缺陷表象可归结为如下几种情况。

1）集抄数据全失：采集不到相应表号的电量数据，通常是由于导入集中器的用户关联信息错误、表计故障或安装错误引起。

2）部分日数据缺失：常因信道干扰或通信模块接触不良引起。缺失发生在当期首日或下月首日时无法确定出账电量，需核抄；若非上述情况，虽当月可出账，但隐藏的硬件或信道质量问题很可能影响后续月集抄出账电量的准确性，故仍应及时消缺。

3）总分电量不匹配：通信故障产生无效数据或电能表内部存储数据错乱引起。

4）集抄冻结电量下降：往往由采集终端软件故障或信道干扰引起。若发生在月初或月末，会导致出账电量错误、甚至为负。

5）集抄冻结电量异常突升：同样由采集终端软件故障或信道干扰引起，表象为电量冻结值维持多日几乎不变（集抄失灵），而后突然较大幅度上升。突增幅度与集抄失灵持续天数有关，例如：图1中序列4当月第5天的冻结值较前一日上升了2 209 kW·h（该日前有125天集抄失灵）；序列5在第6～8日及15～25日集抄失灵，致使9日和26日的冻结值分别较前一日增加了80 kW·h和224 kW·h，增幅大致是失灵期用电量的累计值。这种集抄失灵导致的异常突增较常见，发生在月初或月末时会严重影响出账电量准确性。

上述缺陷中前4类很好判定，第5类缺陷的准确判定是一个难点。这是因为，季节交替月份气温的变化（例如春夏交替月份日最高气温上升至35℃以上）或是用户用电行为变化（如出差或度假后回家）也会造成冻结电量序列斜率的突增，而这2种都属正常用电情况。因此，在判定集抄数据异常突增类缺陷时，不仅要找出不光滑的序列，还要对异常突增和正常突增加以甄别。

2 集抄数据异常突增的判定方法

考虑按月实施集抄数据缺陷分析的问题，下文仅针对总电量序列，对分费率电量序列异常突增的判定方法类似。

在甄别出1.2节中第（1）～（4）类缺陷后，需从剩余计量点中去除月用电量很低（算例中取≤15 kW·h/月）的计量点。此类用户对营销电费收益的影响很小，且往往具有间歇性用电的特点、不宜采用光滑性分析的方法判定集抄数据异常。经上述两步后的剩余计量点实施异常突增点判定。

2.1 基于光滑比分析的疑似缺陷判定

设第i个计量点当期（指出账电量对应的周期）第k日总电量冻结值为Ei（k）。为弱化冻结电量绝对值大小对光滑性判定结果的影响，首先将冻结值折算到当期首日冻结值为0的基准下并标幺化，公式为

式中：n为当期天数。按式（1）计算所得的序列Xi=（xi（2），xi（3），…，xi（n））称为“累计电量序列”（accumulated consumption series，ACS）。

由第1节分析可知，若集抄冻结值存在异常突增点，则其ACS非光滑，反之不然。故可依据光滑比初筛疑似存在异常突增的ACS序列。为此，计算如下两序列：

1）光滑比序列：光滑比等于序列元素与其前序元素累计和值之比，即

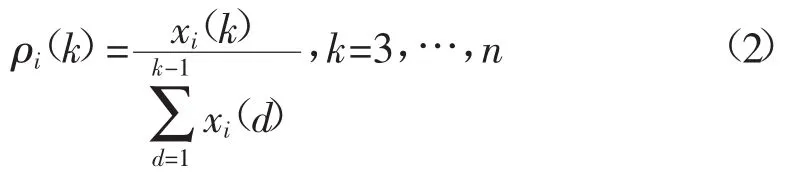
2）光滑比的级比：级比为序列中相邻2个元素之比，光滑比级比的计算式为

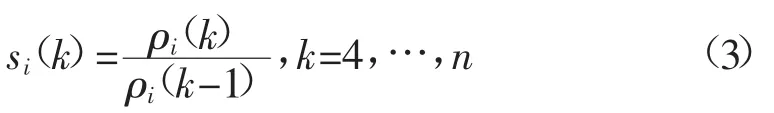
根据序列光滑性的定义[10]，若一ACS序列满足如下2个条件之一，就判定该序列疑似存在异常突增点：

2.2 基于Lipschitz指数分析的二次判定

ACS异常突增与正常突增的一个重要差别是：前者的增幅对应集抄失灵期用电量的累计值，该值往往远大于突增后几日的增幅，从而使得异常突增表现为阶跃型的突变；后者在突变日的冻结电量增幅则与一日用电量相当，同时也与突变后几日的每日增幅相当，这使得正常突增表现为斜坡型突变。在小波分析中，这2类突变具有不同的Lipschitz指数，可利用这点加以区分。

2.2.1 Lipschitz指数的定义

在信号奇异性（指信号在某处间断或其导数不连续）分析中，用Lipschitz指数α描述奇异点的不光滑度。

定义1[8，11]：设n为非负整数，n＜α≤n+1，若存在2个常数A和h0＞0以及n次多项式pn（h），使得对∀h≤h0均有

则称f（x）在点x0处的Lipschitz指数为α。

Lipschitz指数表明了函数f（x）与n次多项式相比的光滑程度，其值越小则函数在点x0处变化越剧烈[8]。在各类突变中，斜坡型突变点α=1，阶跃型突变点α=0，突变介于两者之间时α处于0～1之间[12]。因此，可通过Lipschitz指数接近0或接近（或等于）1来辨别ACS中的异常/正常突变。

2.2.2 Lipschitz指数的求解

小波变换是信号f（x）与小波基函数Ψ（x）的卷积运算，即

式中：s称作小波基函数的伸缩尺度。

定义2[11，13]：若对x0邻域内的任意点x有|Wf（s0，x）|≤|Wf（s0，x0）|，则称（s0，x0）为小波变换模极大值点。在（s，x）构成的尺度空间中，连接模极大值点得到的线称作模极大值线。

已有文献证明[11]，f（x）在点x0为Lipschitz α的充要条件是：∃常数A，使得x0的影响锥内所有模极大值点（s，x）都满足

上式可变换成

因此，x0处的Lipschitz指数α是横坐标log2s、纵坐标log2|Wf（s，x）|）构成的对数坐标中，高于log2|Wf（s，x）|的直线的斜率，该值即收敛于x0的模极大值线切线的斜率。

基于上述原理，Lipschitz指数的求取按如下步骤进行[14]：

1）对疑似存在异常突增的ACS进行小波变换。鉴于haar小波对阶跃信号具有最强的检测效果[13]，本文以haar作为小波基。

2）根据小波系数确定各尺度上的模极大值，并从s=0的每一模极大值点（0，x0）出发，将尺度空间内邻近的、具有相同符号的模极大值连接起来，构成模极大值线。

3）对每一收敛于（0，x0）的模极大值线，求取其拟合函数切线的斜率，该斜率就是奇异点x0处的Lipschitz指数。

3 算例分析

以上海市北供电公司辖区内54台集中器某年7月采集的数据为例。采集成功的低压计量点数共计5 879个，去除部分数据缺失、总分不匹配、冻结电量有下降点三类缺陷后的计量点有4 520个，对这些计量点进一步实施异常突增判定。

3.1 光滑比分析结果

对4 520个计量点当月ACS实施光滑比分析，据第2.1节判据，疑似存在异常突增点的ACS有1 200个。不过，从图2可见：无论阶跃型突增还是斜坡型突增，都会引起ACS的光滑比上升（对应级比大于1）。这表明，单靠光滑比分析无法准确区分两类突增，须进一步评估Lipschitz指数加以区别。

3.2 基于Lipschitz指数的二次判定结果

对1 200个疑似异常突增计量点实施以haar为基的小波分析，并搜索Lipschitz指数取值在[0，1]间的奇异点。图3同样以图1中序列2～5 4种典型ACS为例，小波变换和奇异点Lipschitz指数计算结果，对每一序列的4张图顺序为原始ACS、各尺度下的小波系数、模极大值线和奇异点Lipschitz指数值。对比后可见。

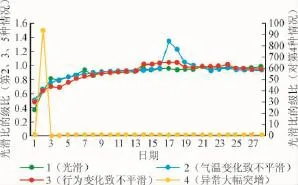
图2 4类典型非光滑的累计用电量序列的光滑比之级比Fig.2 Stepwise ratios of the smooth ratios of four typical unsmooth accumulated consumption series

1）由于日用电量受多种随机因素的干扰，ACS中除存在一些显著的斜坡型突变外，还可能存在一些不很显著的奇异点，它们反映了相邻两日用电量的较大变化。这些奇异点的Lipschitz指数基本在0.5～1之间，斜坡型突变越显著，α越接近1。

2）ACS的异常突增点并不是标准的阶跃型突变，但对应的Lipschitz指数非常接近于0。本例中序列4在第4点、序列5在第27点的Lipschitz指数分别为0.06和0.05。

据上述规律，可以Lipschitz指数处于[0，0.1]为判据辨识出异常突增点，相应的计量点有325个。

3.3 与经验判据的对比

分别采用文献[6-7]的经验判据，对同一组计量点同月集抄数据实施异常突增的判定。其中，对文献[7]的判定思想，以用户每日8 h按运行容量的3倍用电来确定阈值。表1列出了几种方法判定结果，可见：

表1 本文方法与经验判据判定结果的比较Tab.1 Comparison of the judgment results by the presented methods and the empirical criteria

1）文献[7]与文献[6]的判据相比，前者可找到较多集抄异常突增点。这是由于文献[6]以日用电量大于300 kW·h为阈值判定异常突增，而本算例研究对象多为运行容量为2～6 kW的低压用户，对应日用电量阈值为48～144 kW·h，不如文献[6]的判据严格。

2）与文献中的经验判据相比，本文方法可搜索出更多异常突增点。这是由于文献[7]的判据隐含了用户正常用电情况下用电功率接近运行容量的假设，对不满足该假设的的集抄数据异常突增缺乏搜索能力；而本文采用的光滑性分析方法本质上考察ACS增长率的连贯性，与日用电量的绝对水平无关。这正是基于序列光滑性分析方法与经验判据的根本差异。

图3 4种典型非光滑累计电量序列小波变换和Lipschitz指数计算结果Fig.3 The wavelet transformation results and Lipschitz exponents of four typical unsmooth accumulated consumption series

4 结论

本文在分析累计用电量正常、异常序列特征的基础上，着重对集抄失灵导致的累计电量异常突增提出了一种基于序列光滑性分析的判定方法。算例分析表明：

1）对累计电量序列实施光滑比分析可有效缩小异常突增的疑似范围，但无法区分异常和正常突增。

2）对疑似异常突增的累计电量序列实施haar小波变换，以Lipschitz指数接近于0为判据，可准确找到异常突增点。

3）与现有经验判据相比，本文方法对集抄异常突增具有更强的搜索能力。

本文研究成果对提高集抄出账准确率具有一定意义。

[1]李翀，唐如意，柴奕春，等.用电信息采集系统低压集中抄表典型台区问题分析及处理[J].河北电力技术，2013，32（4）：31-34.LI Chong，TANG Ruyi，CHAI Yichun，et al.Treatment on lower voltage centralized meter reading typical area based on electric energy data acquisition system[J].Hebei Electric Power，2013，32（4）:31-34（in Chinese）.

[2]黄贵星.电网低压载波集中抄表系统应用效果评价及改进研究[D].北京：华北电力大学专业硕士学位论文，2011.

[3]WU N，GUO Y，WEI Y，et al.Design of the remote wireless meter reading system based on GPRS[J].Telkomnika Indonesian Journal of Electrical Engineering，2013，11（11）:6358-6366.

[4]杨宏伟，孟令新.影响电量集抄系统抄表成功率的常见故障分析及对策[J].山东电力技术，2005（3）：64-65.YANG Hongwei，MENG Lingxin.The EMS’s common failure analysis and relevant counter measures[J].Shandong Electric Power，2005（3）:64-65（in Chinese）.

[5]顾国栋，周玉，钱立军，等.用电信息采集系统集抄用户采集成功率提升研究[J].江苏电机工程，2013，32（6）：29-31.GU Guodong，ZHOU Yu，QIAN Lijun，et al.Research on the improvement of the data acquisition success rate of power-consuming information acquisition system[J].Jiangsu Electrical Engineering，2013，32（6）:29-31（in Chinese）.

[6]钱立军，李新家.用电信息采集系统中数据审查策略与异常原因分析[J].电力需求侧管理，2013，15（1）：45-47.QIAN Lijun，LI Xinjia.Strategy of the data checking and the exception reason analysis in the information collection system[J].Power DSM，2013，15（1）:45-47（in Chinese）.

[7]康丽雁，王志斌，孙飞跃.电力用户用电信息采集系统不良数据分析及处理方法[J].东北电力技术，2012，33（11）:46-48.KANG Liyan，WANG Zhibin，SUN Feiyue.Abnormal data analysis and processing method for power user electric energy data acquisition system[J].Northeast Electric Power Technology，2012，33（11）:46-48（in Chinese）.

[8]刘娜，杨秀媛，何谨，等.电厂热力设备检测中的Lipschitz指数分析[J].中国电机工程学报，2002，22（3）: 118-120.LIU Na，YANG Xiuyuan，HE Jin，et al.Lipschitz exponent analysis to detection of thermal systems in power plants[J].Proceedings of the CSEE，2002，22（3）:118-120（in Chinese）.

[9]王楠，律方成.基于小波奇异性检测的在线监测数据处理[J].电工技术学报，2003，18（4）：61-64.WANG Nan，LÜ Fangcheng.On-line monitoring data processing based on wavelet singularity detection[J].Transactions of China Electrotechnical Sociey，2003，18（4）: 61-64（in Chinese）.

[10]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2004.

[11]MALLAT S，HWANG W L.Singularity detection and processing with wavelets[J].IEEE Transactions on Information Theory，1992，38（2）:617-643.

[12]徐长发，李国宽.实用小波方法（第三版）[M].武汉：华中科技大学出版社，2009.

[13]徐丙莲，羿旭明.基于小波变换的信号奇异性分析[J].数学杂志，2004，24（6）：661-664.XU Binglian，YI Xuming.The singularity detection of signal based on the wavelet transform[J].Journal of Math，2004，24（6）:661-664（in Chinese）.

[14]连可，王厚军，龙兵.一种基于小波变换模极大值的估计Lipschitz指数新方法[J].电子学报，2008，36（1）：106-109.LIAN Ke，WANG Houjun，LONG Bing.A novel method of measuring Lipschitz exponent based on wavelet transform modulus maxima[J].ACTA Electronica Sinica，2008，36（1）:106-109（in Chinese）.

[15]黄永高，卢毅.基于小波分析和灰色模型的用电量预测[J].电网与清洁能源，2011，27（3）：34-37.HUANG Yonggao，LU Yi.Electricity consumption forecasting based on wavelet analysis and gray model[J].Power System and Clean Energy，2011，27（3）:34-37（in Chinese）.

[16]孙红革，张娟.电能计量远程抄表系统的应用及改进措施[J].陕西电力，2007，35（4）：81-82.SUN Hongge，ZHANG Juan.Application and improvement measures of remote electricity meter reading system[J].Shaanxi Electric Power，2007，35（4）:81-82（in Chinese）.

[17]朱玉泉，李振林.联合站能耗灰色关联分析[J].节能技术，2008，26（152）：560-563.ZHU Yuquan，LI Zhenlin.Grey relational analysis on the energyconsumption ofoilfield combination station[J].Energy Conservation Technology，2008，26（152）:560-563（in Chinese）.

（编辑 徐花荣）

Data Abnormality Judgment for the Central Metering Systems Based on Time Series Smoothness Analysis

YANG Haitao1，2，MOU Tingting1，YANG Haitao1，XIN Jieqing1
（1.Key Laboratory of Control of Power Transmission and Conversion，Ministry of Education，Shanghai Jiaotong University Shanghai 200072，China；2.Shibei Power Supply Company，SMEPC，Shanghai 200240，China）

Discriminating abnormal data uprushes caused by the central metering system malfunction from normal consumption increases is the main difficulty in the metering data defect analysis.A method based on smoothness analysis of daily consumption series（DCS）is presented in this paper for this purpose.Suspected defective DCS are firstly searched out by smooth ratio analysis.The haar wavelet transformation is further applied to these suspected series and Lipschitz exponents are calculated for their singular points.Since abnormal uprushes manifest themselves as staircase changes，true defect series are identified by searching singularities with Lipschitz exponents close to zero.A numerical example is presented based on the real central metering data collected by Shibei Power Supply Company of SMEPC.Results show that，compared with the existing empirical criteria，the proposed method is of greater defect discovery ability.Research findings of this paper have practical significance for improving the accuracy of electricity billing under the central metering environment.

central metering systems；data abnormality judgment；smooth ratio；Lipschitz exponent；wavelet analysis

国家自然科学基金重点项目（51337005）；国家电网公司科技项目资助（52091414007Y）。

Project Supported by the National Natural Science Foundation of China（51337005）；Science and Technology Project of State Grid Corporation of China（52091414007Y）.

1674-3814（2016）08-0073-06

TM93

A

2016-02-22。

杨海涛（1976—），男，高级工程师，主要研究方向为电力营销和电能计量管理；

牟婷婷（1992—），女，硕士研究生，研究方向为数据挖掘技术在集抄数据分析中的应用；

杨海滔（1994—），女，硕士研究生，研究方向为电力营销和电力市场；

辛洁晴（1973—），女，副教授，研究方向为电力营销，智能用电管理和电力市场。