不同堆积结构颗粒床内的流动特性研究

李良星,邹旭毛,孔刘波

(西安交通大学动力工程多相流国家重点实验室,710049,西安)



不同堆积结构颗粒床内的流动特性研究

李良星,邹旭毛,孔刘波

(西安交通大学动力工程多相流国家重点实验室,710049,西安)

为了研究不同堆积结构颗粒床内的流动特性,使用两种尺寸球形颗粒构建了均匀混合堆积结构和分层堆积结构床,在碎片床冷却性实验装置(DEBECO,DEbris BEd COolability)上进行了单相和两相流动实验。基于实验结果,对比分析了两种堆积结构的流动阻力压降,进一步验证了流动阻力模型。实验结果表明:对于不同尺寸颗粒均匀混合的堆积颗粒床,其有效直径在低速(Rep<7)条件下更接近面积平均直径;随着速度(Rep>7)升高,其有效直径更接近长度平均直径。当气液两相同向向上流过均匀堆积结构颗粒床时,实验测量的两相压降总体上与Reed模型预测值较为接近;与均匀堆积结构床相比,相同颗粒分层堆积结构床内的两相流动阻力压降较低。该实验研究结果对完善多孔介质结构内流动阻力分析具有重要的学术意义。

堆积颗粒床;均匀堆积床;分层堆积床;流动特性;阻力压降

颗粒堆积多孔介质结构内的单相/两相流动在许多工程和科学领域中都有着广泛的应用和研究,涉及农业技术、生物工程、机械工程、石油化工工程、核动力工程等多个领域[1-4]。与传统连续介质结构相比,颗粒堆积多孔介质内部结构呈现出明显的多尺度结构特性。由于多孔介质结构孔隙的多向性,流体在多孔介质中不停地发生混合和分离,流速的大小和方向不断地发生改变,因此多相流体运动的控制方程呈现高度非线性特征,很难用物理实验或理论解析对多孔介质内的流动现象进行精确的描述和研究。因此,传统的流动阻力模型及相关理论不能直接应用在多孔介质材料内的流体流动过程。

许多研究者已针对多孔介质结构内的流动特性开展了深入的实验和理论研究,并提出了不同的流动阻力模型。文献[5-6]回顾和总结了上述研究及相关模型,然而这些研究大多是基于均匀堆积结构的颗粒床,关于非均匀堆积结构如颗粒分层堆积结构颗粒床的研究还相对较少。在熔融物与冷却剂相互反应的实验研究中[7-8],实验结果获得了分层结构的颗粒碎片床。而且,近期基于分层结构颗粒床的沸腾传热实验[9-10]表明,与均匀堆积结构颗粒床相比,分层结构颗粒床的传热恶化情况明显不同。然而,强烈的沸腾现象掩盖了堆积颗粒床内的流动特性,这些研究也仅仅给出了测量获得的分层结构颗粒床的干涸热流密度,并没有给出分层结构颗粒床内的流动特性及其对传热恶化的影响机理。

因此,为了探究不同堆积结构颗粒床内的流动特性,本文在西安交通大学动力工程多相流国家重点实验室的碎片床冷却性实验装置(DEBECO)上进行了均匀堆积结构颗粒床和分层堆积结构颗粒床的单相和两相流动实验。基于实验结果,对比分析了两种堆积结构的流动阻力压降,并进一步验证了流动阻力模型。

1 实验系统

1.1 实验装置

为了研究堆积颗粒床内的流动特性,西安交通大学动力工程多相流国家重点实验室设计和搭建了DEBECO实验系统,如图1所示。

图1 DEBECO实验系统图

整个系统由供水系统、供气系统、气水混合段、实验测试段及实验数据测量和采集系统构成。实验装置的主体部分由透明的树脂玻璃建成,其中实验测试段为圆柱形,内径120 mm、高度600 mm,颗粒在测试段内堆积成多孔介质结构的实验床。在测试段的底部和顶部的法兰连接处,分别放置不锈钢网栅,用于支撑和固定堆积颗粒床。为了确保流量测量的精确性,气相、液相流量由不同量程范围的流量计进行测控。为了减少压力测量误差,实验过程同时采集不同高度差下对应的压力信号和压差信号,压力传感器和差压变送器的精度分别为0.25%和0.04%。实验过程中采用美国国家仪器有限公司生产的NI数据采集系统对温度、压力等信号进行采集整理。

1.2 实验颗粒床

本文基于Φ1.5 mm和Φ6 mm两种尺寸的球形颗粒,堆积了4种颗粒床,依次命名为Bed-1～Bed-4,4种颗粒床的总高度均为600 mm,详细信息如表1和图2所示。其中Bed-1和Bed-2分别由Φ1.5 mm和Φ6 mm的单一尺寸颗粒堆积而成;Bed-3由Φ1.5 mm和Φ6 mm颗粒按照1∶1的质量比均匀混合堆积组成;Bed-4是由Φ1.5 mm和Φ6 mm颗粒分层堆积组成,其中上层为Φ1.5 mm颗粒,下层为Φ6 mm颗粒,两者质量比为1∶1。由此可见,Bed-1～Bed-3为均匀堆积结构颗粒床,而Bed-4为分层堆积结构颗粒床。

图2 不同结构的颗粒实验床

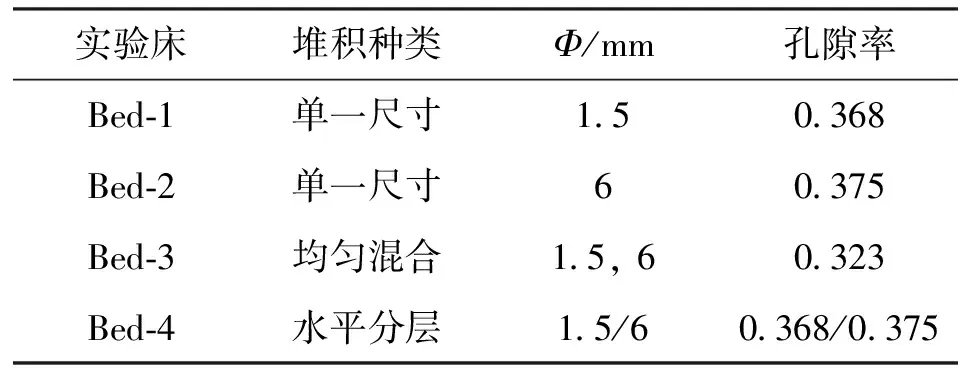
实验床堆积种类Φ/mm孔隙率Bed⁃1单一尺寸150368Bed⁃2单一尺寸60375Bed⁃3均匀混合15，60323Bed⁃4水平分层15/60368/0375

2 颗粒床内流动阻力模型介绍

为了研究分析颗粒堆积多孔介质结构内的流动特性,研究者提出了很多的分析模型和经验关系式,其中心思想是分析预测多孔介质结构内的单相、两相流动阻力。其中,Ergun方程[11]由于其表达形式简便,易于计算,而且具有较高的计算精度,目前已被普遍接受和广泛应用于球形颗粒组成的多孔介质内单相流动的阻力预测分析中,其表达式如下

(1)

式中:dp/dz为实验床内的压降梯度;μ是流体的黏度;ρ是流体的密度;J是多孔介质内流体的表观速度;K和η分别被称为渗透率和穿透率,表达式如下

(2)

其中150和1.75是基于实验而得到的经验常数,被称为Ergun常数,ε是多孔介质的孔隙率,d是组成多孔介质床的颗粒有效直径。

通过引入相对渗透率Kr和相对穿透率ηr,Ergun方程进一步扩展到多孔介质结构内的两相流动特性研究中,如下式所示

(3a)

(3b)

式中:Jl和Jg分别代表两相流动中液相和气相的表观速度;α是多孔介质结构单元内的截面含气率;Fi是相间摩擦力。表2列出了不同研究人员给出的两相流动模型的基本参数,其中s表示多孔介质结构单元内的饱和度,s=1-α。

表2 不同模型的基本参数

对于Schulenberg & Müller模型,其对应相间摩擦力表达式如下

(4)

从表2可以看出,不同的模型对参数Kr、ηr和Fi选取了不同的表达式。显然,不同模型对相同工况下同一个颗粒床内的流动阻力压降的预测计算值是不同的,这给工程计算和应用带来极大的不确定性。因此,本文将基于实验数据,通过对比上述模型的计算结果,来分析验证不同模型的预测计算能力。

3 实验结果及分析

3.1 单一尺寸颗粒堆积床内单相/两相流动特性

首先进行了单一尺寸颗粒堆积床内单相流动实验,图3显示了单相水自下而上流过颗粒床Bed-1和Bed-2时测量的阻力压降值。由于Ergun方程已被广泛应用于单一球形颗粒床内单相流动阻力压降的预测计算,因此图3中也分别给出了基于Bed-1和Bed-2流动工况的Ergun方程计算值。

图3 Bed-1和Bed-2内单相流动阻力压降

由图3可以看出,对单一尺寸颗粒堆积床如Bed-1和Bed-2,其单相流动阻力压降随液速升高而非线性增大,速度越高,增速越快。与大尺寸颗粒堆积床(Bed-2)相比,小尺寸颗粒堆积床(Bed-1)内的单相阻力压降明显较高,说明颗粒孔隙率相差不大时,颗粒尺寸越小,颗粒堆积床内单相阻力压降越高。与Ergun方程的计算值相比,Bed-1和Bed-2的实验测量值与其吻合得很好,标准偏差在7%以内。这一方面进一步说明了Ergun方程对单一球形颗粒堆积床内单相流动阻力的准确计算能力,另一方面也检验了整套实验装置的运行和测量精度。

与单相流动不同,研究者对堆积颗粒床内两相流动压降预测模型还没有形成统一的认识。由表2可以看出,不同的研究人员给出的不同的参数表达式,对于相同实验工况,其计算结果必然存在一定的差异。为了对比验证两相流动阻力模型的预测能力,本文基于单一尺寸颗粒堆积床,进行了气-水两相流动实验,进而对比不同模型的预测计算值与实验测量的两相流动摩擦阻力压降的差异。图4显示了气-水同向竖直向上通过Φ1.5 mm球形颗粒堆积床时测量的两相流动摩擦阻力压降,同时也给出了表2中不同预测模型的计算值。由图4可以看出,当液速保持不变时,随着气速的增加,颗粒床内两相压降逐渐升高。与实验测量值相比,Hu & Theofaneous模型[14]和Schulenberg & Müller模型[15]预测计算值偏高,Lipinski模型[12]计算值偏低,总体上Reed模型[13]的预测值与实验值更为接近。

图4 Bed-1内两相流动摩擦阻力压降

3.2 不同尺寸颗粒均匀混合堆积床内单相/两相流动特性

由Ergun方程可以看出,堆积颗粒的有效直径是流动压降计算的重要参数。对单一尺寸球形颗粒堆积床,颗粒直径即为有效直径,然而对多尺寸颗粒均匀混合堆积床,其有效直径的计算则依据不同的理论分析和参考权重,不同的研究人员采用了不同的计算方法。其中,最为常用的有效直径d计算方法有4种[16],分别被称为质量平均直径dm、面积平均直径da、长度平均直径dl和数目平均直径dn,表达式分别如下

(5)

(6)

(7)

(8)

式中:fi是颗粒尺寸分布在(xi,xi+Δx)范围内的数量;mi、ai、li和ni分别是颗粒质量分布、面积分布、长度分布和数量分布的函数。依据式(5)～(8),Bed-3的质量平均直径、面积平均直径、长度平均直径以及数量平均直径分别为3.75 mm、2.4 mm、1.76 mm和1.57 mm。

图5显示了单相水竖直向上流过Bed-3时测量的流动阻力压降,同时绘制了Ergun方程基于不同有效直径的计算值。

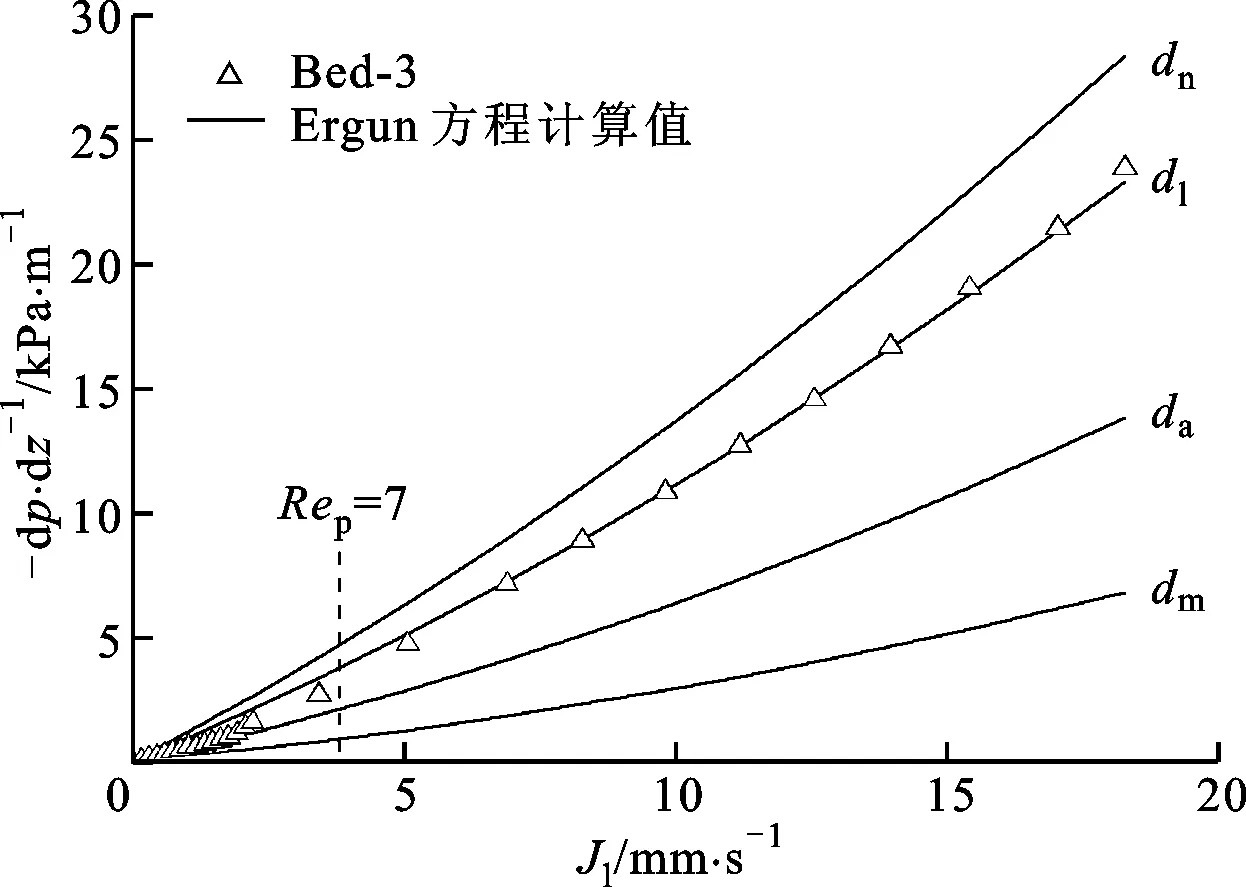
图5 Bed-3内单相流动阻力压降

由图5可以看出:当流速较低(Rep<7)的时候,Ergun方程基于面积平均直径进行计算的理论值与实验值吻合较好;随流速增大(Rep>7),实验值更接近于采用长度平均直径计算的Ergun方程理论值。其中,多孔介质内流体雷诺数的定义如下

(9)

图6绘制了气-水两相自下而上通过Bed-3时实验测量的两相流动摩擦阻力压降。实验时液速以0.29 mm/s的速度保持恒定,而气速逐渐增大。为验证两相流动阻力模型,图6也绘制出了表2中不同模型的计算值。由于实验中液速较低,因此模型计算时有效直径采用面积平均直径。由图6可以看出,总体上Reed模型[13]的预测值与实验测量值更为接近。

图6 Bed-3内两相流动摩擦阻力压降

3.3 分层堆积结构颗粒床内单相流动特性

实验中测量了分层堆积结构颗粒床上部、下部单一颗粒床内的阻力压降和整个实验床的总压降,分别用p1.5、p6和ps表示,其测量示意图如图7所示。

1:不锈钢网栅;2:连接法兰;3:导压管;4:气液分离罐;5:差压变送器;6:实验段图7 分层堆积床压力测量示意图

图8显示了实验测量的各部分阻力压降变化,可以看出,对于下层的Φ6 mm颗粒堆积床,其Ergun计算值与实验值吻合很好,说明分层结构对其下层Φ6 mm颗粒堆积床内的单相流动几乎没有影响,然而上层Φ1.5 mm颗粒堆积床内实验测量的阻力压降明显高于Ergun方程计算值。颗粒床的总压降介于上层颗粒床和下层颗粒床的平均压降之间,高于下层的Φ6 mm颗粒床的压降,低于上层Φ1.5 mm颗粒床的压降。

图8 Bed-4内单相流动阻力压降

为了进一步分析分层结构对其流动特性的影响,本文首先对比了Bed-1和Bed-4中Φ1.5 mm颗粒堆积床内的单相流动压降,如图9所示。

图9 Bed-1和Bed-4上层颗粒床内的单相流动阻力压降

由图9可以看到,分层堆积颗粒床Bed-4内上层Φ1.5 mm颗粒床内的单相阻力压降明显高于Φ1.5 mm颗粒堆积床Bed-1内的阻力压降。与Bed-1相比,Bed-4的上层结构与Bed-1没有区别,颗粒的尺寸及孔隙率完全相同,但是Bed-4的下层是由颗粒直径更大、孔隙率更高、同等情况下单相阻力压降更低的Φ6 mm颗粒组成。换而言之,同样的流动工况下,Bed-4的下层产生了更低的流动阻力,由于分层结构的影响,Bed-4的上层虽然和Bed-1有相同的颗粒尺寸和孔隙率,但是其单相流动阻力压降却明显升高,这说明分层结构对颗粒堆积床内的流动特性有明显影响。

图10 Bed-3和Bed-4的阻力压降

本文还对比了Bed-3和Bed-4的单相流动阻力压降。Bed-3和Bed-4是由相同比例相同尺寸的两种颗粒堆积而成,不同的是Bed-3是由两种尺寸颗粒均匀混合堆积而成,而Bed-4是由同样的两种尺寸分层堆积而成。图10显示了Bed-3和Bed-4内单相流动阻力压降的实验测量结果。由图10可以看出,在相同的条件下,Bed-3均匀混合的实验床的阻力压降高于Bed-4分层堆积结构床。分析认为,Bed-3内两种尺寸均匀混合堆积产生了更小的孔隙率,由表1可知仅为0.323,远低于Bed-4中每一层颗粒床的孔隙率,由Ergun方程可知其较低的孔隙率而导致了较高的流动阻力。换而言之,对具有相同的尺寸分布和质量分布颗粒群组,颗粒分层堆积床会比颗粒均匀混合堆积床产生更低的阻力压降,这将有利于高温沸腾条件下产生较高的干涸热流密度,进而有利于反应堆严重事故背景下碎片床的冷却。

4 结 论

为了探究不同堆积结构颗粒床内的流动特性,本文在西安交通大学动力工程多相流国家重点实验室的DEBECO实验系统上进行了均匀堆积结构颗粒床和分层堆积结构颗粒床的单相和气-水两相流动实验。基于实验结果,对比分析了颗粒均匀堆积结构和颗粒分层堆积结构实验床内的流动阻力压降,进一步验证了两相流动阻力模型,主要结论如下。

(1)对于不同尺寸颗粒均匀混合的堆积颗粒床,面积平均直径在低速(Rep<7)条件下更接近其有效直径。随速度升高,其有效直径更接近长度平均直径。

(2)当气液同向流过颗粒均匀堆积床时,总体上Reed模型的计算值最接近实验测量的两相阻力压降值。

(3)颗粒分层堆积结构对流动特性影响明显,与单一尺寸颗粒堆积床相比,分层结构产生了更高的流动阻力压降;与不同尺寸颗粒均匀混合堆积床相比,同样条件下的颗粒分层堆积床产生了更低的流动阻力压降,这有利于反应堆严重事故背景下碎片床的冷却。

[1] HOLDICH R G. Fundamentals of particle technology [M]. Leicestershire, UK: Midland Information Technology and Publishing, 2002: 1-4.

[2] JAMIALAHMADI M, MULLER-STEINHAGEN H, IZADPANAH M. Pressure drop, gas hold-up and heat transfer during single and two-phase flow through porous media [J]. International Journal of Heat and Fluid Flow, 2005, 26(1): 156-172.

[3] BEAR J. 多孔介质流体动力学 [M]. 李竞生, 等译. 北京: 中国建筑工业出版社, 1983: 1-18.

[4] 杜新龙, 低渗透砂岩油层微流动机理研究 [D]. 成都: 西南石油大学, 2012.

[5] 闫晓, 肖泽军, 黄彦平. 多孔介质中流动换热特性的研究进展 [J]. 核动力工程, 2006, 27(1): 77-82. YAN Xiao, XIAO Zejun, HUANG Yanping. Research progress on flow and heat transfer in porous media [J]. Nuclear Power Engineering, 2006, 27(1): 77-82.

[6] BAI B, LIU M, LV X, et al. Correlations for predicting single phase and two-phase flow pressure drop in pebble bed flow channels [J]. Nuclear Engineering and Design, 2011, 241(12): 4767-4774.

[7] KARBOJIAN A, MA W M, KUDINOV P, et al. A scoping study of debris bed formation in the DEFOR test facility [J]. Nuclear Engineering and Design, 2009, 239: 1653-1659.

[8] MAGALLON D. Characteristics of corium debris bed generated in large-scale fuel-coolant interaction experiments [J]. Nuclear Engineering and Design, 2006, 236: 1998-2009.

[9] NAYAK A K, SEHGAL B R, STEPANYAN A V. An experimental study on quenching of a radially stratified heated porous bed [J]. Nuclear Engineering and Design, 2006, 236(19/20/21): 2189-2198.

[10]THAKRE S, LI L, MA W. An experimental study on coolability of a particulate bed with radial stratification or triangular shape [J]. Nuclear Engineering and Design, 2014, 276: 54-63.

[11]ERGUN S. Fluid flow through packed columns [J]. Chemical Engineering Progress, 1952, 48(2): 89-94.

[12]LIPINSKI R J. A one dimensional particle bed dryout model [J]. ANS Transactions, 1981, 38: 386-387.

[13]REED A W. The effect of channeling on the dryout of heated particulate beds immersed in a liquid pool [D]. Cambridge, USA: Massachusetts Institute of Technology, 1982.

[14]HU K, THEOFANOUS T G. On the measurement and mechanism of dryout in volumetrically heated coarse particle beds [J]. International Journal of Multiphase Flow, 1991, 17(4): 519-532.

[15]SCHULENBERG T, MÜLLER U. An improved model for two-phase flow through beds of course particles [J]. International Journal of Multiphase Flow, 1987, 13(1): 87-97.

[16]李良星, 李会雄. 多尺寸颗粒堆积多孔介质床有效直径研究 [J]. 工程热物理学报, 2014, 35(9): 1785-1788. LI Liangxing, LI Huixiong. An study on effective diameter of packed porous media bed with multi-size particles [J]. Journal of Engineering Thermophysics, 2014, 35(9): 1785-1788.

(编辑 荆树蓉)

Investigation on the Flow Characteristics in Particulate Beds with Different Packing Structures

LI Liangxing,ZOU Xumao,KONG Liubo

(State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To investigate the flow characteristics in particulate beds with different packing structures, the experiments on flow characteristics of particulate homogeneous and stratified beds consisting of two kinds of spherical particles were performed on the test facility of DEBECO (DEbris BEd COolability). Based on the experimental results, the pressure drops were compared and analyzed, and the flow resistance models were further verified. The experimental results showed that the effective diameter is closer to the area mean diameter at low flow rates (Rep<7) for a bed packed with uniform mixture of particles, but more closer to the length mean diameter with increasing flow rates (Rep>7). For gas-water cocurrent flow through a homogeneous bed, the predictions of Reed’s model were more comparable with the measured pressure drops. Compared with the homogeneous bed filled with the same particles, the stratified bed showed a lower flow resistance. The experimental results may contribute to the analysis of flow resistance in porous media.

packed bed; homogenous bed; stratified bed; flow characteristics; pressure drop

2016-01-11。 作者简介:李良星(1979—),男,副教授。 基金项目:国家自然科学基金资助项目(51406143);陕西省自然科学基础研究计划资助项目(2015JM5237)。

时间:2016-06-08

10.7652/xjtuxb201609008

TK124

A

0253-987X(2016)09-0049-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160608.1035.008.html