桁架结构拓扑及截面尺寸优化设计方法

周奇才,吴青龙,熊肖磊,王璐

(同济大学机械与能源工程学院,201804,上海)



桁架结构拓扑及截面尺寸优化设计方法

周奇才,吴青龙,熊肖磊,王璐

(同济大学机械与能源工程学院,201804,上海)

为克服传统基结构设计方法对最优解的束缚,实现桁架结构的拓扑布局及尺寸优化,提出了将连续体与离散杆系相结合的桁架结构优化设计方法。从连续体出发,基于SKO连续体拓扑优化方法得到了最优拓扑布局;以二值图像细化算法为基础,提出了基于有限单元8邻域网格模型的骨架提取算法,通过剥离冗余单元,得到了连续体拓扑优化结果的中心传力骨架;以单元主应力为判据,精确找到骨架中的关键点,并连接关键点形成了初始桁架结构;基于拉格朗日乘数法和Kuhn-Tucker条件,以初始桁架中杆件的内外半径为设计变量,结构体积为约束条件,结构柔度为目标函数,建立了桁架结构杆件尺寸优化的数学模型,并推导出其优化迭代准则。最后,以一悬臂结构为例对该优化方法的应用进行了说明,并使用一经典算例与其他文献中的方法进行了对比,结果表明:该优化方法得到的桁架结构具有优化的拓扑构型和力学特性,杆件布局、尺寸合理,应力均匀。

桁架;连续体;拓扑优化;骨架提取;尺寸优化

桁架结构因具有造价低、重量轻、施工简便的特点而在工程领域中得到了广泛应用。桁架结构的优化设计包扩结构的拓扑和布局优化及杆件的尺寸优化。在桁架拓扑和布局优化方面,Michell于1904年提出的Michell桁架理论以及Prager于1977年建立的经典布局理论为其奠定了理论基础,而Dorn等提出的基结构法则标志着桁架拓扑优化工作的真正开始[1-2]。在随后的若干年中,几乎全部研究都是基于基结构展开的。这些研究主要包括基于尺寸优化的拓扑优化[3-4],基于独立变量的拓扑优化,以及集拓扑、形状和尺寸于一体的布局优化[5]。基于基结构进行拓扑优化,所得的优化解本质上是给定基结构中的一个子集,因此基结构的采用其实一开始就限制了优化解的范围,并且真正的最优解很可能没有包含在该范围内。为消除基结构的限制,一些非基结构法的桁架拓扑、布局优化方法相继出现。例如:Giger等利用数学图论对桁架结构进行参数化建模,结合遗传算法实现摆脱了基结构的桁架拓扑优化[6];Mroz等借鉴生物生长规则,由基础结构出发,不断添加杆件生成了最优拓扑结构[7];Azid等采用遗传算法的思想,在给定载荷和约束作用点的情况下,突破基结构束缚实现了桁架的智能布局优化设计[8]。在杆件尺寸优化方面,广泛使用的是满应力法,采用满应力准则调整截面尺寸,使每根杆件充分发挥其承载性能,达到满应力状态[9-10]。

本文提出一种与上述方法均不相同的桁架结构优化设计方法:将连续体拓扑优化和离散体拓扑优化相结合,避免了传统桁架优化中基结构对优化结果的限制,可最大限度地寻求结构的最优拓扑分布;将桁架结构拓扑优化和尺寸优化分离开来,使用连续体优化寻求结构的最优拓扑,使用骨架提取算法抽离骨架得到桁架布局,最后建立桁架杆件尺寸优化的数学模型,并使用拉格朗日乘数法和Kuhn-Tucker条件推导出杆件截面尺寸的优化迭代准则。优化方法的流程如图1所示。

图1 桁架拓扑优化流程

1 连续体拓扑优化

连续体拓扑优化采用SKO(soft kill option)方法,这是一种基于生物自适应生长规律的启发式连续体结构拓扑优化方法,最早是由德国的Karlsruhe研究中心提出的[11-12]。

SKO算法流程图如图2所示,其核心迭代关系式为

(1)

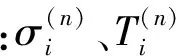
图2 SKO算法流程图

SKO算法通过每次有限元分析中单元的应力情况不断地更新单元温度,进而改变结构中单元的材料信息,最终删除软化的单元,获得优化的拓扑结构。

2 骨架提取

连续体拓扑优化后的结果包含较多的冗余单元信息,为将其转换为桁架结构,需去除冗余的单元信息,找到中心骨架。目前,在结构优化领域尚未见到对连续体拓扑优化结果进行简化进而提取中心骨架的相关文献。本文借鉴图像处理中的二值图像细化算法[13],结合有限元模型中的网格特性,提出一种基于有限单元8邻域网格模型的骨架提取算法。该算法可直接应用于各种低阶和具有中间节点的高阶四边形单元,但要求有限元模型具有规则的网格划分,并且在骨架提取算法中使用的均为单元顶点节点,中间节点不参与骨架提取运算。该算法不适用于使用三角形单元或自由网格划分形成的不规则有限元模型。

连续体拓扑优化后的结果中包含优化单元(优化后保留下来的单元)和背景单元(优化后删除的单元)。在有限元模型中,每一个优化单元周围都可视为有8个单元与之相邻接(边界上的单元可假设背景单元与之相邻接),称为该单元的8邻域。通过对每个单元的8邻域单元的判断,可将冗余优化单元转化为背景单元,最终剩下的单元即为骨架单元。单元模型和单元的8邻域如图3所示。

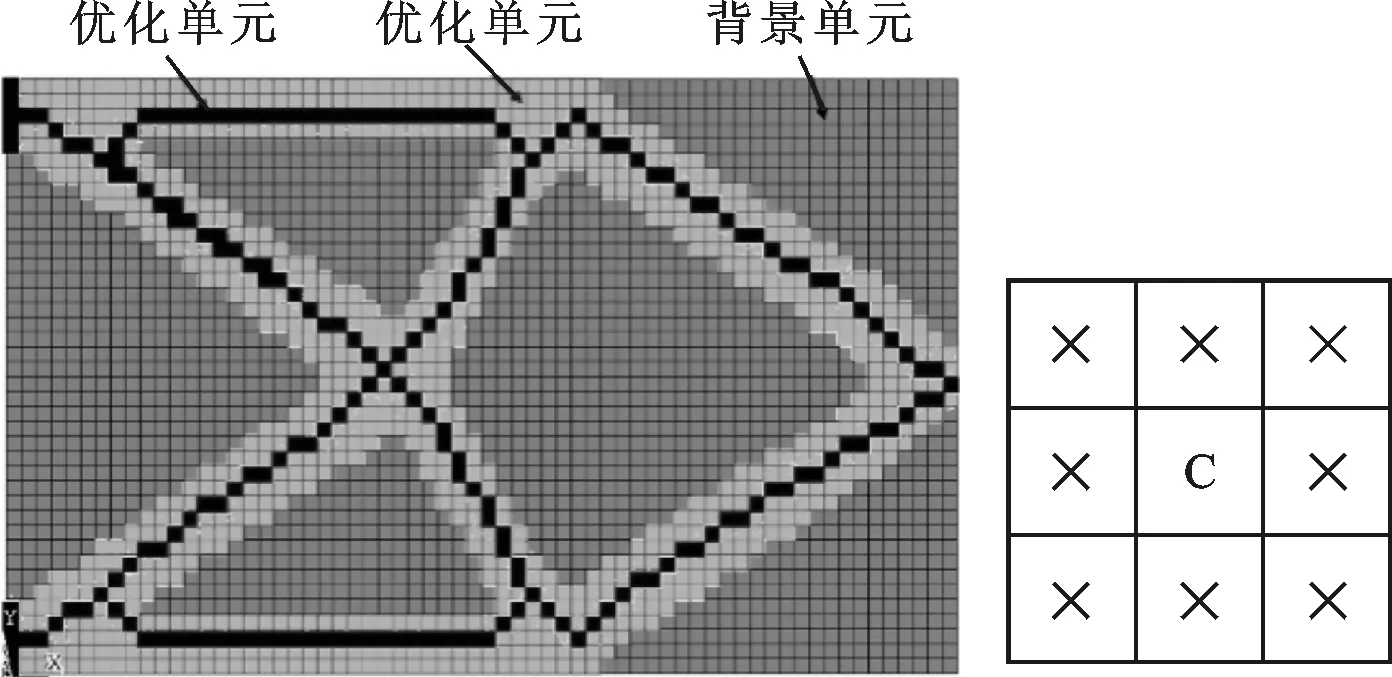
图3 单元模型和单元的8邻域

2.1 骨架提取算法流程

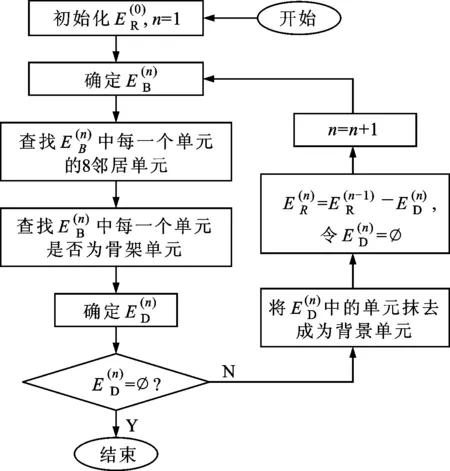
图4 骨架提取算法流程图

2.2 8邻域单元查找模型

要判断当前单元是否为骨架单元,需要先找出当前单元对应位置的8邻域单元及其对应单元的信息。如图5所示,假设当前单元ec的8邻域单元按图示的ec1～ec8的顺序排列,则需要依次判断出ec1～ec8所在的8个位置的单元分别是背景单元还是优化单元。

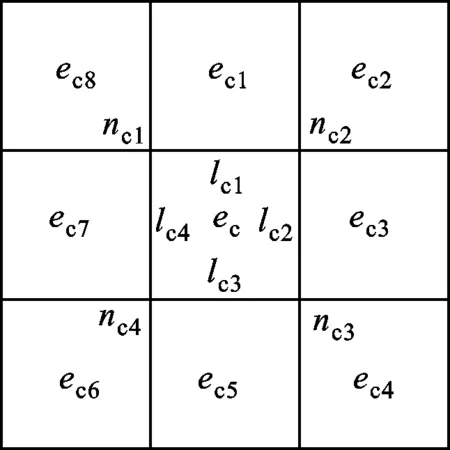
图5 8邻域单元查找模型

为查找出当前单元的8邻域单元,首先对有限元网格模型约定如下基本定义。

定义1 网格(G)、单元(E)、线(L)的表达形式为

G(E,L,N),E(L,N),L(N)

(2)

分别表示网格由单元、线、节点组成,单元由线、节点组成,线由节点组成。

定义2 E、L、N表示网格中所有单元、线、节点的集合

(3)

定义3 若构成四节点平面单元ex的节点集为{nx1,nx2,nx3,nx4},则ex可表示为

ex=(nx1,nx2,nx3,nx4)

(4)

定义4 同时含有节点ni,nj,…的单元的集合表示为

Ex(ni,nj,…)

(5)

定义5 单元ec的8邻域:单元ec的上下左右4个相邻单元及对角线上的4个相邻单元组成的集合即为单元ec的8邻域单元

Eec={ec1,ec2,…,ec8}

(6)

在上述定义的基础上,当前单元ec的8邻域单元查找方法如下。

(1)首先找到当前单元ec的节点集{nx1,nx2,nx3,nx4}。

(2)通过算法式(7)定位ec1、ec3、ec5、ec7所在位置的单元

(7)

式中:Ec={ec},表示当前单元;∩和为集合的交、差运算符。

(3)通过算法式(8)定位ec2、ec4、ec6、ec8所在位置的单元

(8)

至此,可获得当前单元ec的8邻域单元Eec={ec1,ec2,…,ec8}。找到对应的8邻域单元后,提取单元信息并存储,为单元判断做准备。

2.3 骨架单元判断算法

若判断某单元为非骨架单元,则将其抹去成为背景单元。判断算法如下。

首先,提出以下定义。

定义6 若单元ex为优化单元,则有|ex|=1;若ex为背景单元,则有|ex|=0。

定义7 A(ec)为当前单元ec的8-邻域单元中优化单元的数目

(9)

定义8 定义B(ec)为当前单元ec的8邻域单元按ec1-ec2-…-ec8-ec1的顺序转一周从背景单元变为优化单元的次数

||ec1|-|ec8||)

(10)

在上述定义6～定义8的基础上,若当前单元ec的8邻域单元满足条件式(11)或式(12),则认为ec为非骨架单元

(11)

(12)

式中:条件2≤A(ec)≤6用于保证删除的单元为边界单元,同时保证骨架的端点不会被删除;条件B(ec)=1保证删除单元不会破坏骨架的连通性;式(11)的后2个条件保证删除的单元处于模型的右侧边界、下侧边界和左上角边界;式(12)的后2个条件保证删除的单元处于模型的左侧边界、上侧边界和右下角边界。在上述条件约束下,即可保证从边缘向内部逐步删除非骨架单元,得到最终的骨架。

3 形成桁架结构

得到连续体优化拓扑结构的骨架后,即找到了优化拓扑的中心路径。此时,只要找到骨架中的关键节点,并依据连续体优化模型的拓扑关系连接关键节点,就可形成具有优化拓扑和布局的桁架结构。

由于连续体优化拓扑模型的复杂性和骨架提取算法的缺陷,得到的骨架可能会有如下问题:

(1)骨架不一定是标准的直线;

(2)在拓扑分支的交界处骨架将会呈现复杂性和不规则性;

(3)骨架可能不经过约束和载荷作用点。

针对以上问题,骨架关键节点的提取需综合考虑约束和载荷作用点、骨架、优化的连续体拓扑结构及其应力分布情况来进行确定。关键点确定的基本原则是:尽量使得到的桁架结构在关键点的受力状态与连续体中该点的应力状态一致,即杆件的布局方向与单元主应力方向保持一致。具体方法如下:

(1)在提取骨架时,人为设定所有载荷和约束作用点为骨架点,并依据骨架提取结果,选择与骨架直接相连的约束作用点作为桁架的约束关键节点;

(2)为保证形成的桁架结构是直杆相连,将骨架中的拐点作为关键节点,连接拐点形成初始桁架,由于拓扑分支交界处骨架的复杂性,交界处将形成复杂的过渡桁架;

(3)桁架结构主要是轴向拉压受力,而在单元体的主应力方向上,切向应力为0,表现为拉压状态,因此需绘制拓扑优化结果的主应力矢量图,依据单元的主应力方向选择合适的关键点,对第(2)步中得到的初始桁架进行简化和修正,形成最终的桁架布局。

4 桁架结构尺寸优化算法

初始得到的桁架结构仅具有优化的拓扑构型,要得到最优桁架结构还需对结构中杆件的尺寸进行进一步优化。下面,将以桁架中杆件的截面内径和外径为设计变量、体积为约束条件、桁架结构柔度为目标函数[14],建立桁架杆件截面的优化数学模型;基于拉格朗日乘数法和Kuhn-Tucker条件并结合有限元理论,推导出设计变量的优化迭代准则;根据体积约束,使用泰勒展开式推导出拉格朗日乘子的表达式。

4.1 优化数学模型

以桁架中杆件的截面内、外半径为设计变量,体积为约束条件,桁架结构柔度为目标函数的优化数学模型为

findR=(r1,1,r1,2,r2,1,r2,2,…,ri,j,…,rn,1,rn,2)

s.t.KU=Fi=1,2,…,nj=1,2

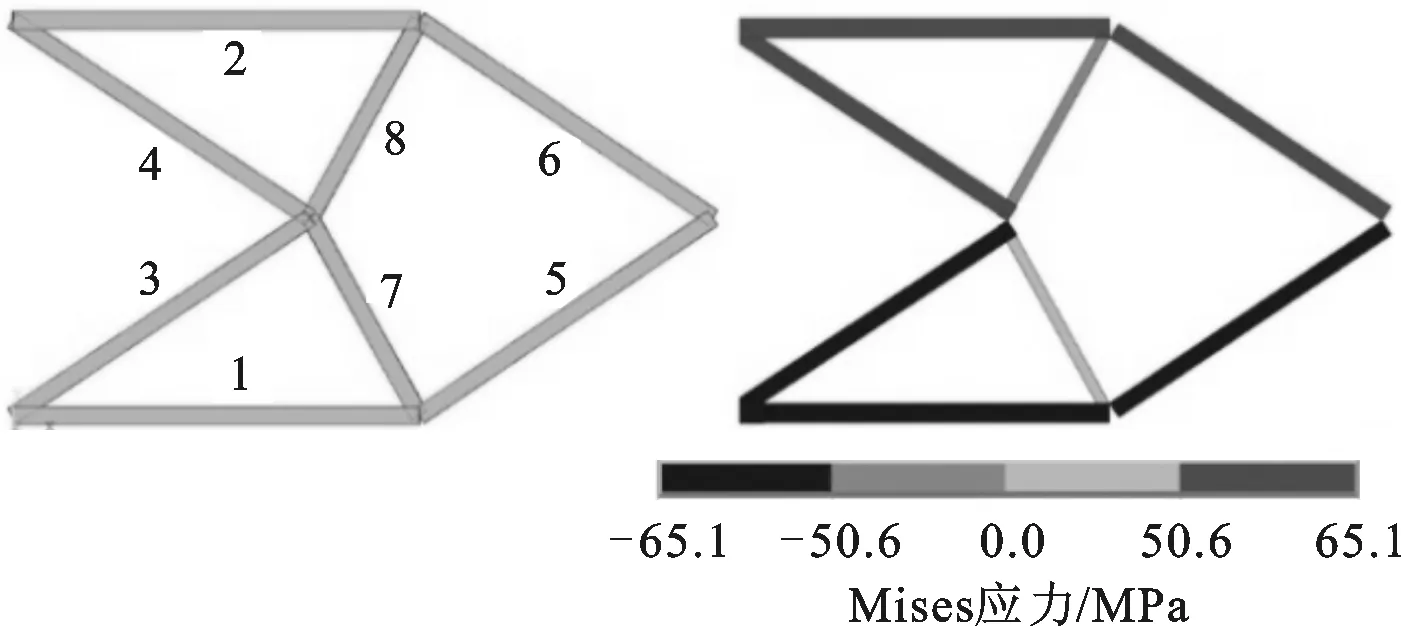
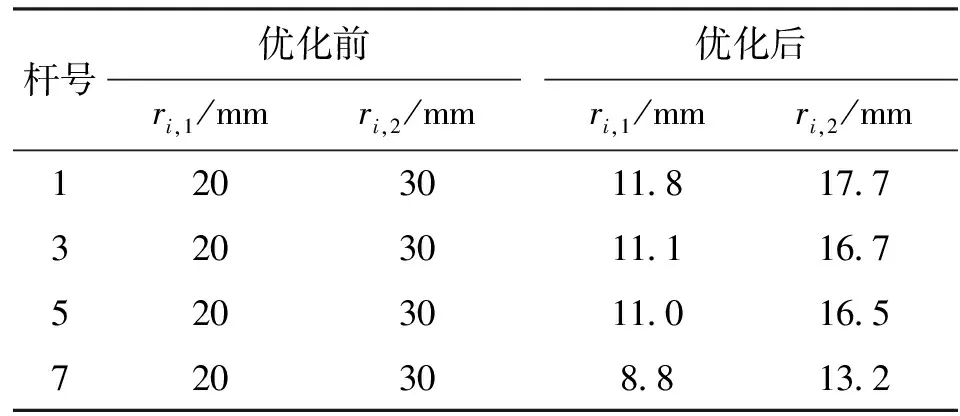
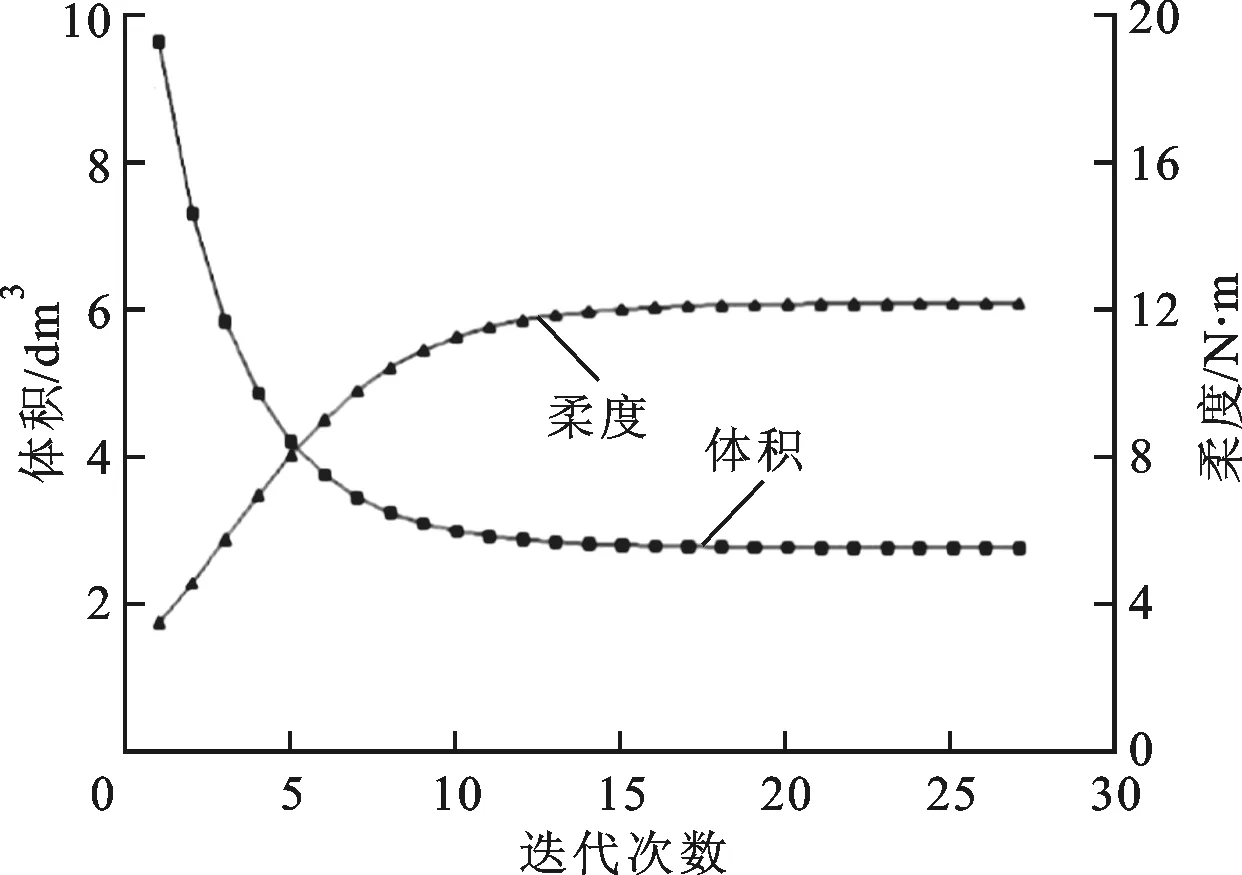
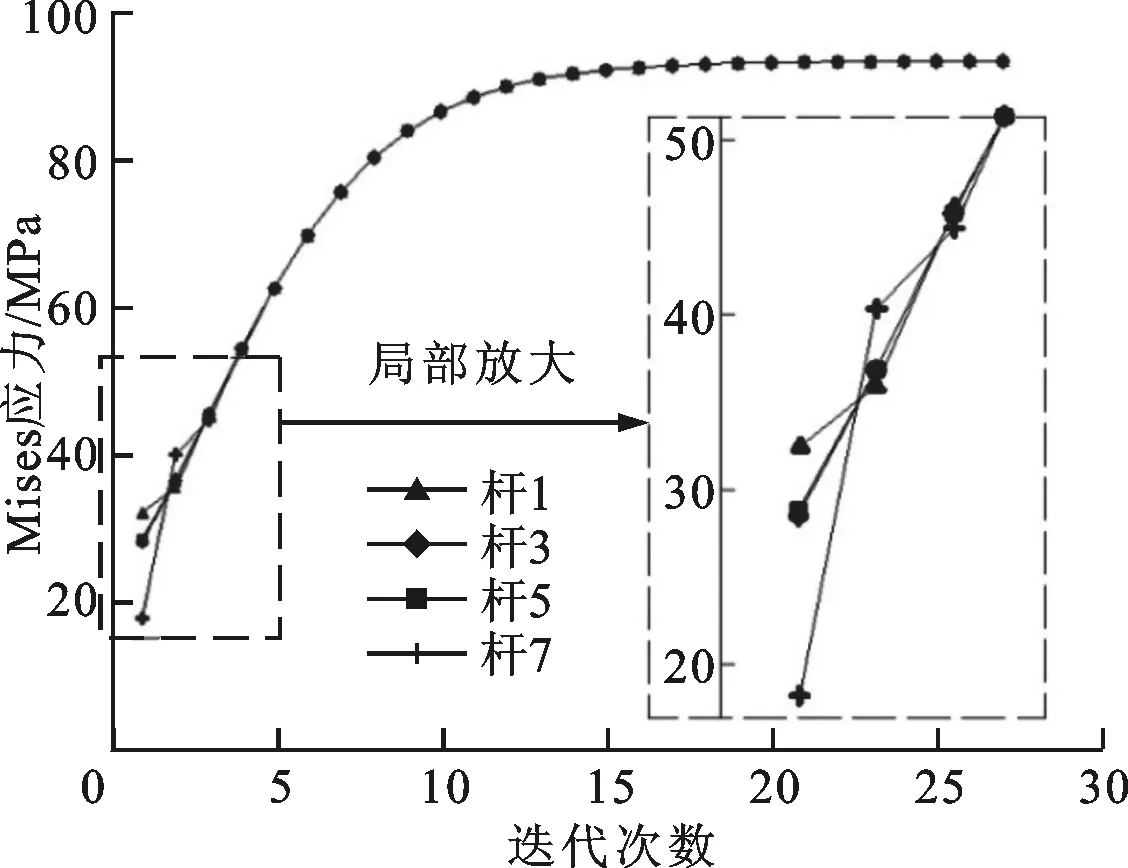
rmin≤ri,1

(13)

式中:ri,1、ri,2为杆件i的内、外半径;R为所有杆件内外半径组成的矢量;n为桁架中杆件的数量;C为结构柔度;U为结构节点的位移矢量;K为结构的总刚度矩阵;ui为i单元节点的位移矢量;ki为i单元的刚度矩阵;F为结构载荷矢量;V为结构体积;V*为约束体积;rmin、rmax为半径的下限和上限。

4.2 优化准则推导

对式(13)表示的数学模型采用拉格朗日乘数法,构建如下拉格朗日函数

(14)

式中:λ1、μ1、μ2、μ3、μ4为拉格朗日乘子,其中λ1为矢量;x1、x2、x3、x4为松弛变量。

针对设计变量R取得极值R*时的情况,当ri,1=rmin时,设计变量半径的下限起约束作用,有μ2>0,μ3=0;当ri,2=rmax时,设计变量半径的上限起约束作用,有μ4>0,μ3=0,;当rmin

(15)

(16)

将C=UTKU代入式(16),得到

(17)

由刚度矩阵的对称性可知

(18)

将式(18)代入(17),并考虑λ1为结构平衡约束拉格朗日乘子,因结构平衡始终满足,故λ1可取任意值,这里取λ1=-2U,式(17)可简化为

(19)

整理后得

(20)

在有限元理论中,二维杆单元的刚度矩阵为

(21)

单元刚度矩阵ki和单元体积vi对杆单元内、外半径的偏导数为

(22)

(23)

式(20)可化为

(24)

整理后得

(25)

(26)

式(26)即为通过拉格朗日函数和Kuhn-Tucker条件推导出的杆件截面尺寸优化准则,它反映了单元截面尺寸与应变能在优化过程中应满足的关系。将fi作为迭代准则,可以得到杆件截面尺寸的迭代公式

(27)

式中:δ为阻尼系数。引入δ可减缓优化进程,保证数值计算的收敛性和稳定性。

4.3 拉格朗日乘子计算

(28)

(29)

假设V(k+1)正好满足体积约束要求,即V(k+1)=V*,则可以求得

(30)

5 算例说明

5.1 算例1——算法流程示意

5.1.1 问题描述 如图6所示,在一个1.6 m×1.0 m的区域内设计一桁架结构,区域左侧为约束端,右侧边缘中部作用一方向向下、大小为50 kN的力F。

图6 算例示意图

5.1.2 优化设计流程 具体优化设计流程如下。

(1)在设计区域上建立连续体有限元模型,依据设计要求施加约束、载荷并进行有限元分析。有限元模型和结构的von Mises应力云图如图7所示。

图7 初始连续体有限元模型及应力云图

(2)使用SKO算法对连续体模型进行拓扑优化,得到优化的连续体拓扑结构及优化结构的von Mises应力云图,如图8所示。

图8 SKO算法优化后的有限元拓扑及应力云图

(3)人为设定优化模型中的约束和载荷作用点为骨架点,并使用骨架提取算法提取优化模型的骨架,见图9a;再选择与骨架直接相连的约束点(A、B)、载荷点(C)和骨架的拐点作为关键点,连接关键点形成初始桁架,如图9b所示。

(a)骨架 (b)初始桁架图9 骨架及初始桁架

图10 主应力矢量图及关键点调整示意

绘制拓扑优化结果的主应力矢量图,如图10所示。因为桁架结构是轴向受拉压的杆件,所以可依据单元的主应力图对初始桁架进行调整和简化。在本例中,对图中①、②、③区域的关键点布局进行调整。从区域①的主应力矢量图中可以看出,主应力方向均指向A点,因此可将图9中的I、J、K点简化到A点。区域②的简化需寻找到一点,使得该区域能良好过渡。该点的选取原则为:使该点的主应力方向与杆JL和CM的夹角α、β大致相同,且与杆DN基本垂直。这样,以该点作为节点形成的桁架在该节点的受力将与连续体优化结果中该点的应力状态一致,这个点就是图10中的点E。对于区域③,因结构的对称性,需要找到第一主应力和第三主应力相等的点,即点D。

连接各新的关键点形成调整后的桁架布局,如图11所示。

图11 调整后的桁架布局

(4)建立桁架结构的有限元模型,使用上述尺寸优化算法进行桁架杆件的尺寸优化。优化前、后的桁架有限元模型及应力如图12和图13所示。在本模型中,分别为杆件编号1～8。

图12 初始桁架的有限元模型及应力图

图13 尺寸优化后桁架的有限元模型及应力图

5.2 优化分析

对桁架杆件进行优化时所使用的材料及优化参数如下:碳素结构钢Q235,其弹性模量为206 GPa,泊松比为0.3,体积约束为30%,半径下限为5 mm,阻尼系数为0.3。杆件初始截面的选取应使结构有足够的优化余量,故内半径ri,1取20 mm,外半径ri,2取30 mm。优化后的半径取值见表1,由于结构的对称性,对称位置的杆件尺寸相同,所以表中仅列出了杆1、3、5、7的尺寸。

表1 杆件优化前后的尺寸

图14所示为尺寸优化过程中,目标函数(桁架柔度)和约束条件(体积)随优化迭代次数的变化情况,结构初始体积为9.64×10-3m3,初始柔度为3.8 N·m。随着优化的进行,体积逐渐收敛于2.89×10-3m3,满足原先30%的体积约束条件。最终结构柔度收敛于12.2 N·m,验证了算法的收敛性和稳定性。

图14 桁架柔度和体积的优化过程

图15 桁架杆件应力的优化过程

图15所示为优化过程中桁架杆件的应力变化情况,由于结构的对称性,对称位置杆件的应力绝对值相同,故仅选取了杆1、3、5、7绘制其应力变化趋势图。由图15可见,在初始时各杆件中的应力具有较大差异,随着迭代的进行,各杆件中的应力趋向均匀,最后达到几乎完全相同,表明算法可使结构的应力趋于均匀,符合结构优化设计的满应力准则。优化前、后各杆件的具体应力值如表2所示。

表2 杆件优化前后的应力值

优化后的应力为93.65 MPa。若要更加充分地利用材料,可以在优化参数中调整体积约束和半径的下限。

5.3 算例2——算法验证

图16所示为桁架结构优化中的经典算例模型,现以该模型为例进行算法的有效性验证。在以下2种工况下,求满足约束的最小质量桁架:工况1,F1=445 kN,F2=0;工况2,F1=0,F2=445 kN。约束条件为各节点的y向位移小于5.08 cm。杆件材料为铝,弹性模量E=68.97 GPa,密度ρ=2 768 kg/m3,许用应力[σ]=172.4 MPa。截面积取离散值{6.45,19.35,32.26,51.61,67.74,77.42,96.77,109.68,141.94,154.84,167.74,180.64,187.10,200.00,225.81} cm2。

图16 算例2示意图

算例中2种工况的处理方法为:在拓扑优化时,为得到满足2种工况的优化拓扑构型,2种工况同时加载,求得最优拓扑构型;在尺寸优化时,对2种工况分别进行优化,然后取优化结果的并集(即杆件的截面尺寸取2种工况单独优化结果中的较大值)。相关文献和本文的优化结果对比如图17和表3所示,可以看出在相同约束条件下,本文算法得出的桁架质量较参考文献的明显减小,且结构应力更均匀,从而验证了本文算法的有效性。

图17 不同算法的桁架布局及杆件尺寸优化结果示意图

参数文[15]文[16]文[5]本文ai/cm2杆11806416774967710968杆2967796771677410968杆396771096851616774杆419351935141946774杆53226193551617742杆6141941096877425161杆7109681419496775161杆8109685161杆910968杆1010968m/kg20113196511998417154u1，max/cm2546320915272312σ1，max/MPa128691500174789588u2，max/cm5077506550755062σ2，max/MPa5738512371885580

ai:杆件截面积;u1,max,u2,max:工况1、2下结构的最大y向位移;σ1,max,σ2,max:工况1、2下结构中的最大应力。

6 结 语

本文提出了一种将连续体与离散桁架结构相结合的桁架优化设计方法。这种方法不同于现有的桁架结构优化设计方法,是利用连续体寻找结构的优化拓扑和布局,使用骨架提取方法获取优化拓扑路径并生成桁架结构,再基于拉格朗日乘数法和Kuhn-Tucker条件推导出优化准则对桁架杆件进行优化。该优化方法结合了拓扑优化、图像处理和优化准则法,能稳定地收敛于约束条件,得到的桁架具有优化的拓扑布局和杆件尺寸,杆件应力均匀,因此有望为桁架结构的优化设计提供一种新的思路。

[1] 姜冬菊, 张子明. 桁架结构拓扑和布局优化发展综述 [J]. 水利水电科技进展, 2006, 26(2): 81-86. JIANG Dongju, ZHANG Ziming. A review on topology and layout optimization of truss structures [J]. Advances in Science and Technology of Water Resources, 2006, 26(2): 81-86.

[2] MICHELL A G M. The limits of economy of materials in frame structures [J]. Philosophical Magazine, 1904, 47(8): 589-597.

[3] 陈建军, 曹一波, 孙怀安. 多工况下具有体系可靠性约束的桁架结构拓扑优化设计 [J]. 固体力学学报, 2000, 21(1): 11-18. CHEN Jianjun, CAO Yibo, SUN Huaian. Topology optimization with reliability constraint of truss under multi-load [J]. Acta Mechanica Solid Sinica, 2000, 21(1): 11-18.

[4] XU Bin, JIANG Jiesheng, TONG Weihua, et al. Topology group concept for truss topology optimization with frequency constraints [J]. Journal of Sound and Vibration, 2003, 261(5): 911-925.

[5] 姜冬菊, 王德信. 桁架结构智能布局优化设计 [J]. 工程力学, 2009, 26(1): 160-165. JIANG Dongju, WANG Dexin. Intelligent layout optimization design of truss [J]. Engineering Mechanics, 2009, 26(1): 160-165.

[6] GIGER M, ERMANNI P. Evolutionary truss topology optimization using a graph-based parameterization concept [J]. Structural and Multidisciplinary Optimization, 2006, 32(4): 313-326.

[7] MROZ Z, BOJCZUK D. Finite topology variations in optimal design of structures [J]. Structural and Multidisciplinary Optimization, 2003, 25(3): 153-173.

[8] AZID I A, KWAN A S K, SEETHARAMU K N. A GA-based technique for layout optimization of truss with stress and displacement constraints [J]. International Journal for Numerical Methods in Engineering, 2002, 53(7): 1641-1674.

[9] 杨博, 金仁和. 基于满应力法的平面桁架优化 [J]. 钢结构, 2015, 30(3): 18-20. YANG Bo, JIN Renhe. Optimization of plane truss based on full stress method [J]. Steel Structure, 2015, 30(3): 18-20.

[10]郭鹏飞, 韩英仕, 魏英姿. 离散变量结构优化的拟满应力设计方法 [J]. 工程力学, 2000, 17(1): 94-98. GUO Pengfei, HAN Yingshi, WEI Yingzi. Imitate full-stressed design method of discrete variable structure [J]. Engineering Mechanics, 2000, 17(1): 94-98.

[11]MATTHECK C. Design and growth rule for biological structures and their application to engineering [J]. Fatigue and Fracture of Engineering Materials and Structures, 1990, 13(5): 535-550.

[12]丁晓红, 程莉. 基于SKO方法的满应力结构拓扑优化设计 [J]. 中国机械工程, 2009, 20(15): 1765-1770. DING Xiaohong, CHENG Li. Topology optimization of full-stressed structures based on SKO method [J]. China Mechanical Engineering, 2009, 20(15): 1765-1770.

[13]CHEN Y, HSU W. A modified fast parallel algorithm for thinning digital patterns [J]. Pattern Recognition Letters, 1988, 7(2): 99-106.

[14]李东泽, 于登云, 马兴瑞. 不确定载荷下的桁架结构拓扑优化 [J]. 北京航空航天大学学报, 2009, 35(10): 1170-1173, 1178. LI Dongze, YU Dengyun, MA Xingrui. Truss topology optimization with uncertain loading scenarios [J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(10): 1170-1173, 1178.

[15]朱朝艳, 刘斌, 张延年, 等. 复合形遗传算法在离散变量桁架结构拓扑优化设计中的应用 [J]. 四川大学学报, 2004, 35(5): 6-10. ZHU Chaoyan, LIU Bin, ZHANG Yannian, et al. Application of complex genetic algorithm to discrete topology optimization of trusses [J]. Journal of Sichuan University, 2004, 35(5): 6-10.

[16]姜冬菊, 王德信. 离散变量桁架结构拓扑优化设计的混合算法 [J]. 工程力学, 2007, 24(1): 112-116. JIANG Dongju, WANG Dexin. A hybrid algorithm for topology optimization of truss structures with discrete variables [J]. Engineering Mechanics, 2007, 24(1): 112-116.

(编辑 葛赵青)

Optimal Design of Topology and Section Size of Truss Structures

ZHOU Qicai,WU Qinglong,XIONG Xiaolei,WANG Lu

(School of Mechanical Engineering, Tongji University, Shanghai 201804, China)

To achieve the topology and section size optimization of the truss structures without being restricted by the traditional ground structure method, a new optimization method combining continuum with discrete bars is proposed. Starting from continuum and using SKO topology optimization method, an optimal topological layout is obtained. Then based on the FEM 8-neighbourhood elements and binary image thinning method, a skeleton extraction algorithm is put forward to remove the redundant element of the optimal topology and get its central force flow skeleton. Through principal stress calculation of the elements, the key points of the skeleton are found precisely, and the initial truss structure is obtained by connecting these key points. For the optimization of bar section size, a mathematical model is established using section sizes as the design variables, truss volume as the constraint condition and truss flexibility as the objective function. And based on this model the optimization criteria are derived according to the Lagrange multiplier method and Kuhn-Tucker condition. Finally this truss design method is illustrated and verified by two examples. Results show that the optimal structures achieve excellent layout, appropriate bar section sizes and uniform stress distribution.

truss; continuum; topology optimization; skeleton extraction; section size optimization

2016-02-25。 作者简介:周奇才(1962—),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51375345)。

时间:2016-06-12

10.7652/xjtuxb201609001

TH11

A

0253-987X(2016)09-0001-09

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160612.1504.004.html