液桥重开过程的两相格子Boltzmann模型及计算

王宁宁,刘海湖,张楚华

(西安交通大学能源与动力工程学院,710049,西安)



液桥重开过程的两相格子Boltzmann模型及计算

王宁宁,刘海湖,张楚华

(西安交通大学能源与动力工程学院,710049,西安)

根据最近提出并发展的相场格子Boltzmann方法,建立了阻塞气道重开过程的不混溶两相流动模型和计算方法。基于自由能理论、引入指示函数对两相流体界面进行描述,指示函数的演化遵循Cahn-Hilliard方程,具有坚实的物理基础;通过压力分布函数对流场信息进行求解,可有效降低密度梯度离散所诱发的数值不稳定性;引入势能形式的界面张力项,与压力形式的相比可有效抑制界面处的假拟速度。应用该模型对液桥重开的两相流动过程进行了数值研究,并着重分析了毛细数对阻塞液桥演化过程的影响,结果表明,阻塞液桥的轴向厚度变化存在临界毛细数现象,当毛细数大于临界值时,阻塞液桥的轴向厚度随时间逐渐减小,最终发生破裂,实现气道的重开;利用该模型重现了无液滴和有液滴形成的两种气道重开现象,对比研究发现,在无液滴形成的气道重开过程中,壁面经历的压力变化更大。研究工作可为深入认识人体肺气道的生理病理机制、微通道内不混溶两相流体的流动规律提供一定的理论依据。

格子Boltzmann方法;两相流动;微通道;界面张力;液桥重开

航天医学工程领域中,太空失重条件下人体肺呼吸道阻塞与重开现象的重新分配是引起航天员心肺功能异常、血气功能交换障碍的主要原因,相关生理病理机制吸引了很多学者的关注[1]。肺呼吸道内的空气、吸附液膜及管壁组成了复杂的气液弹动力系统,阻塞液桥的破裂将严重影响两相流动状态及空间分布[2]。由于呼吸道解剖结构的复杂性、管壁及其吸附液膜多变的流变性质,所以与阻塞及重开现象相关的呼吸流动机理研究对理论、实验及数值方法均提出了很大的挑战。

Prisk等通过空间实验室研究发现,微重力条件下呼吸道阻塞的临界肺气量与地面环境下的测量值相当,但阻塞发生后将遍及肺部其他区域[3]。Pedley等采用生物力学方法对可塌陷管、槽道内流体/弹性体动力学系统进行了理论及数值研究[4-5],但是未考虑界面张力等因素的影响。Grotberg等采用直接数值模拟方法,对定常界面张力作用下的气道闭合现象进行了分析,发现该现象会导致壁面剪切应力剧烈波动[6]。许世雄等采用刚性直圆管对下呼吸道阻塞液桥重开过程进行了理论和实验研究[7-8]。Malashenko等将肺呼吸道简化建模为刚性直圆管道,并采用VOF(Volume of Fluid)方法研究了阻塞液桥的迁移及破裂过程[9]。Baudoin等实验研究了直管道及多分岔管道中单个或多个液桥同时存在时的流动行为[2]。

格子玻尔兹曼方法(LBM)可以方便地对两相界面进行描述,易于处理复杂几何边界,近年来在微尺度多相流动领域取得了显著的进展[10-12]。本文通过相场LBM两相流动模型[10-11]对阻塞气道的重开过程进行了数学建模和数值计算,重点分析了毛细数对阻塞液桥轴向厚度的影响规律,以及液桥破裂过程中的两相流动现象,以期为深入认识呼吸道阻塞与重开机理、管内两相流体输运技术提供理论参考。

1 液桥重开过程建模

1.1 简化条件

阻塞气道重开现象的本质是管道内气液两相流动及其流型的转变过程,阻塞状态时为弹状流动,重开状态时为环状流动。为了简化该流动物理过程,进行了如下假设[9]:管道壁面是刚性的;忽略液膜的分层及纤毛特性,将液膜简化为牛顿流体,且初始厚度呈均匀分布;不考虑Marangoni应力的作用;初始阻塞液桥形状为圆柱形;附着液膜运动及内部空气流均为不可压缩流动。此外,本文计算条件下Bond数(重力与界面张力之比)远小于1,因此模拟中不考虑重力的作用。

1.2 数学模型及参数条件

阻塞细支气管道二维几何模型[9]如图1所示。深色区域为壁面吸附液膜及阻塞液桥,无色区域为被液桥隔断的空气区域,图中气道为阻塞状态,(xl,yl)为计算域的大小,U为平均气体流速,R为气道半径,h0为通道中液膜的初始厚度,b0为液桥的初始厚度,F0为气体水平方向上施加的外力并驱动两相运动。上、下壁面为无滑移边界条件,入口及出口为周期边界条件。

图1 阻塞气道几何模型图

液桥轴向厚度演化主要与7个无量纲参数相关,即

(1)

式中:下标a表示气相,m表示液膜;t为时间;η为动力学黏度;ρ为密度;Rea为肺气道中空气雷诺数。在人体细支气管道内部Rea=O(1),因此可认为气道中的流动基本为蠕变流,Rea对人体气道流动的影响不大。此外,细支气管内气相、黏液的密度和黏度以及通道内的气体流速通常变化不大,而界面张力系数受年龄、呼吸道疾病等因素的影响具有一定的变化范围。毛细数Ca可以描述界面张力的作用,Ca=ηmU/σ为黏性力与界面张力之比。一般认为,人体细支气管内空气-黏液的界面张力系数σ=0.01～0.1 N·m,对应毛细数Ca=0.1～1。

2 相场LBM两相流动模型

相场LBM两相流动模型,基于自由能的概念、通过指示函数的演化方程自动捕捉两相界面,模型物理意义清晰,同时具有LBM方法本身的各项优点,如易于处理复杂几何边界、程序简单、并行效率高等,因此在模拟人体肺气道阻塞与重开过程中的复杂两相流动问题方面,具有良好的应用潜力。

(2)

(3)

[η(u+uT)]+FS+F0

(4)

μ=φ3-φ-ε22φ

(5)

式中:u为流体的宏观速度;Mφ为移动性参数;p为压力;FS为与界面张力有关的作用力项[12],当界面张力为常数时FS=3×21/2σμφ/4ε;μ为化学势,是指示函数和界面厚度的函数。

(6)

(7)

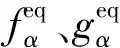
(8)

(9)

(10)

(11)

(12)

式中:ξ为微观粒子速度;I为二阶单位张量;ωα为各离散速度的权系数(ω0=4/9,ω1,2,3,4=1/9,ω5,6,7,8=1/36);Γ为与Mφ有关的可调参数,Mφ=δtΓ(τg-1/2)。宏观量的计算式为

(13)

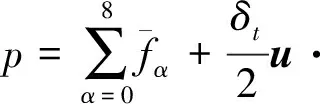
(14)

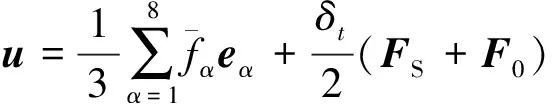
(15)

为模拟两种动力学黏度和密度不同的流体,将运动学黏度υ和密度定义为指示函数的线性函数

(16)

(17)

3 液桥重开过程的模拟结果与分析

3.1 毛细数对液桥演化过程的影响

在Ca=0.1～1.0的范围内,对不同毛细数下的液桥演化规律进行了数值模拟,参数设置为R=50,h0/R=0.2,b0/R=2.0,Re=0.67,其他的与文献[9]的参数设置相同。由计算结果发现,两相演化过程可大致分为3类,如图2所示。

(a) Ca=0.125, (b) Ca=0.182, (c) Ca=0.5, 轴向变厚 轴向不变 轴向变薄图2 3种毛细数下的液桥轴向厚度演化过程

在演化过程中,液桥整体沿流动方向迁移,各毛细数下的初始柱形液桥均快速发展为更接近实际的弯月形液桥,初始阶段受毛细数的影响不大。不同毛细数下阻塞液桥的轴向厚度演化呈现出不同的演化规律,即存在临界毛细数现象。本文模拟获得的临界值为Cacr=0.182,在该临界毛细数下阻塞液桥的轴向厚度在演化后期保持不变,当毛细数大于临界值时,阻塞液桥的厚度随时间减小,反之则增大。

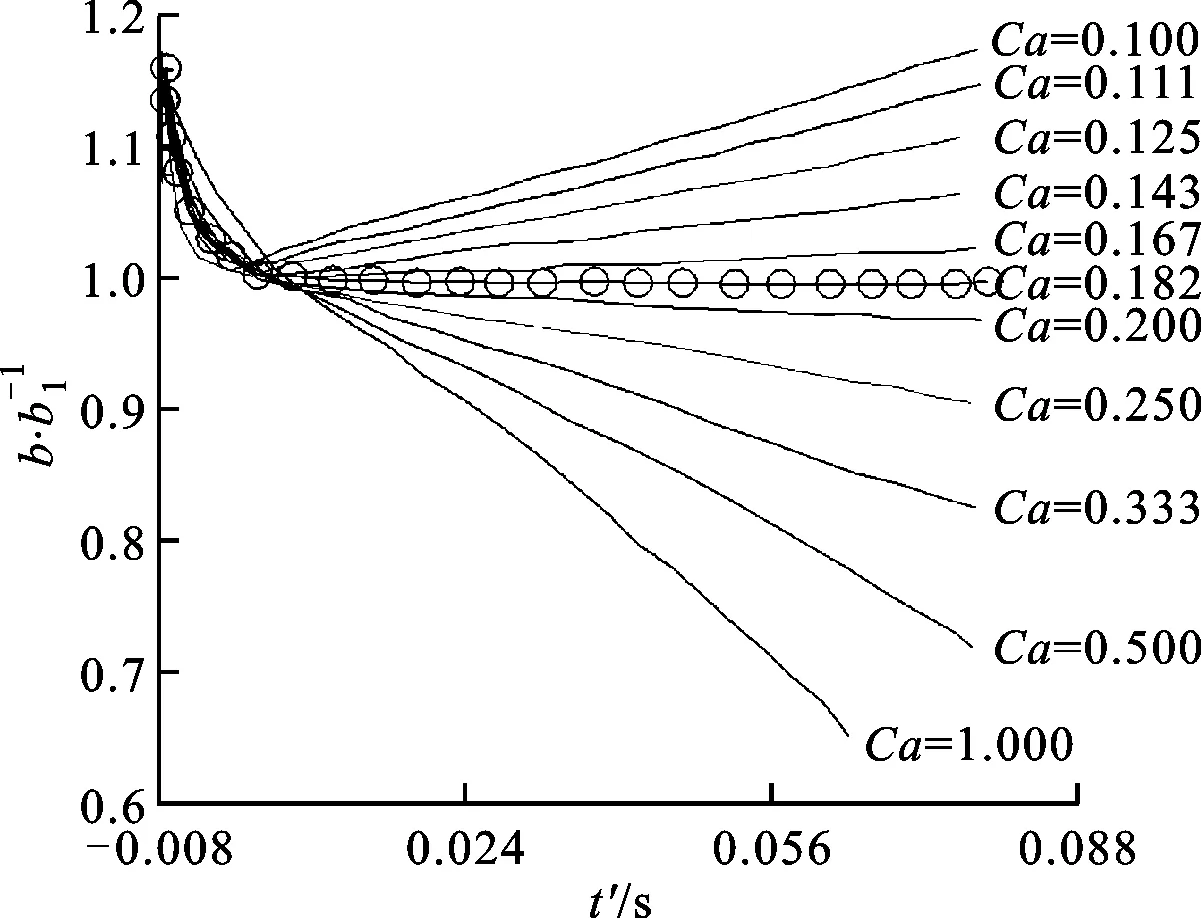
(a)本文模拟结果

(b)文献[9]模拟结果图3 不同毛细数下液桥轴向厚度演化情况

不同毛细数下液桥轴向厚度b的变化趋势如图3所示。由图3a模拟结果可见,各毛细数下,初始阶段形成的液桥厚度几乎相等,本文将该轴向厚度定义为b1,并用于其他时刻轴向厚度的无量纲化处理。为方便结果分析,引入新变量t′=tphy-0.008 s对本文的时间项进行处理,使得t′=0时刻与文献[9]中tphy=0时刻相对应。对比可知:本文模拟所得的临界毛细数与文献[9]的模拟结果相同,均为0.182;在非临界毛细数下,相场LBM获得的液桥厚度演化速率略偏小,总体演化趋势均呈近线性发展,与文献[9]的模拟结果定性地吻合良好,从而验证了相场LBM的有效性和准确性。

为了探究液桥厚度发生变化的原因,本文以毛细数大于临界值的情况为例,给出了液桥及其临近区域的压力分布云图,如图4所示。由压力分布云图可得,以液桥长度在中轴线处的中点B为界,在毛细数大于临界值时液桥上游的压差PAB小于下游的压差PBC,因此相同时间内流入液桥的流体体积小于流出液桥的流体体积,宏观上表现为液桥厚度变薄。其他毛细数下可同理分析。

图4 毛细数大于临界值时的液桥压力分布云图

基于以上结论可知,毛细数高于临界值时,阻塞液桥厚度逐渐减小,且毛细数越大,液桥厚度变化速率越快。因此,当液桥厚度减小至某一临界状态后,液桥的形状将无法继续维持,气道发生重开。

3.2 无液滴形成的液桥重开过程

给定h0/R=0.26,b0/R=0.33,F0=1.5×10-8,对应初始阶段Ca=0.265,Re=1.24。所得模拟结果与文献[9]的模拟结果对比如图5所示。

(a)本文模拟结果 (b)文献[9]模拟结果图5 无液滴形成的液桥重开过程

图5显示,在两相流体沿流动方向迁移的过程中,柱形的阻塞液桥在初始阶段迅速发展为弯月形,并且液桥左侧界面的曲率明显大于右侧。液桥轴向厚度逐渐变薄,中心处变薄的速率最快且最先发生断裂;随着裂口的继续扩大,断裂的液桥径向长度减小,并与上、下壁面附着的贴壁液膜逐渐融合,进而被隔断的两侧流体重新连通,即气道发生重开,重开过程中无液滴生成,该结果与文献[9]吻合良好。

3.3 有液滴形成的液桥重开过程

由文献[2,9,15]知,若液桥体积和毛细数足够大,则液桥重开过程中可能伴随有微液滴生成。为此,设置h0/R=0.2、b0/R=0.83、F0=1.5×10-8,对应初始阶段Ca=1.865、Re=1.867进行模拟,并与文献[9]模拟结果、文献[2]实验结果进行了比较,如图6所示。

(a)本文模拟结果

(b)文献[9]结果 (c)文献[2]结果图6 有液滴形成的液桥重开过程

图6表明,在大初始阻塞液桥体积和毛细数下,本文模拟获得了有液滴形成的液桥重开现象,所得演化过程与文献[9]及文献[2]结果吻合良好。同时看到,柱形液桥很快发展为弯月形,在界面张力及外力场的共同作用下,液桥左侧的气相流体尖端被“拉长”,液桥的轴向厚度逐渐变薄。其与无液滴形成的情况不同在于,左右两侧流体的最初接触位置并非处于气道中轴线,而是在中轴线的两侧各形成了一个裂口,两裂口之间的残余液膜形成了一个小液滴。

3.4 2种液桥重开过程的对比分析

比较以上2种液桥重开现象可知:在液桥破裂之前的短时间内,若液桥左侧界面的曲率半径小于右侧界面的曲率半径,则液桥断裂直接在中轴线处发生,仅形成了一个裂口,不形成小液滴的概率很大;反之,液桥两侧流体在连通时存在2个或多个接触点,接触点之间的液膜被截断后并未及时排出,从而形成了小液滴,该液滴在流动过程中进一步受到主流流动影响,可能破裂为更多的小液滴。此外,液滴生成也取决于液桥破裂前不稳定[9]等因素。

(a)无液滴形成的液桥重开过程

(b)有液滴形成的液桥重开过程图7 2种液桥重开过程中壁面的压力分布变化

为分析管壁在气道重开过程中的受力变化,本文给出了2种液桥重开现象中液桥破裂前后气道壁面上的压力分布变化,如图7所示。无液滴及有液滴形成的液桥重开现象对应的重开时间分别为tphy=0.008 5 s和tphy=0.017 3 s。在无液滴形成的重开过程中,液桥破裂前后其所在区域出现较大的压力突变;在有液滴形成的气道重开过程中,压力幅值在所关注的位置区段内整体增长较小。因此,无液滴形成的气道重开过程对管壁有更大的潜在危害。

4 结 论

(1)基于相场格子Boltzmann两相流动模型,对液桥重开过程的两相流动进行了数值研究,所得模拟结果与相关实验及数值研究结果吻合良好,从而验证了该数值方法的有效性、准确性,体现了该模型在涉及界面拓扑结构变化的复杂两相流动行为方面的模拟能力。

(2)毛细数对阻塞液桥演化过程的影响存在临界毛细数现象,本文获得的临界毛细数为0.182。毛细数小于临界值时,阻塞液桥的厚度随演化过程的进行逐渐增大,气道仍为阻塞状态;反之,阻塞液桥的厚度逐渐减小,实现重开。

(3)毛细数高于临界值时获得了无液滴和有液滴形成的2种液桥重开现象。在无液滴形成的液桥重开过程中,气道壁面上的压力变化更为剧烈,具有更大的潜在危险。

[1] PRISK G K. Invited review: microgravity and the lung [J]. Journal of Applied Physiology, 2000, 89(1): 385-396.

[2] BAUDOIN M, SONG Y, MANNEVILLE P, et al. Airway reopening through catastrophic events in a hierarchical network [J]. Proceedings of the National Academy of Sciences, 2013, 110(3): 859-864.

[3] PRISK G K, GUY H J, ELLIOTT A, et al. Ventilatory inhomogeneity determined from multiple-breath washouts during sustained microgravity on Spacelab SLS-1 [J]. Journal of Applied Physiology, 1995, 78(2): 597-607.

[4] CARPENTER P W, PEDLEY T J. Flow past highly compliant boundaries and in collapsible tubes [C]∥IUTAM Symposium 2001. Neidelberg, Germany: Springer, 2003: 26-30.

[5] LIU H, LUO X, CAI Z, et al. Sensitivity of unsteady collapsible channel flows to modeling assumptions [J]. Communications in Numerical Methods in Engineering, 2009, 25(5): 483-504.

[6] TAI C F, BIAN S, HALPERN D, et al. Numerical study of flow fields in an airway closure model [J]. Journal of Fluid Mechanics, 2011, 677: 483-502.

[7] 许世雄, CHEW Y T, LOW H T, 等. 下呼吸道重开的生物流体力学研究: 理论分析 [J]. 水动力学研究与进展: A辑, 2001, 16(1): 35-43. XU Shixiong, CHEW Y T, LOW H T, et al. Biofluid mechanics investigation on obstructed pulmonary lower airway reopening: theoretical analysis [J]. Journal of Hydrodynamics: A, 2001, 16(1): 35-43.

[8] 许世雄, CHEW Y T, LOW H T, 等. 下呼吸道重开的生物流体力学研究: 实验模拟 [J]. 生物物理学报, 2000, 16(2): 380-386. XU Shixiong, CHEW Y T, LOW H T, et al. Biofluid mechanics investigation on obstructed pulmonary lower airway reopening: experiment simulation [J]. Acta Biophysica Sinica, 2000, 16(2): 380-386.

[9] MALASHENKO A, TSUDA A, HABER S. Propagation and breakup of liquid menisci and aerosol generation in small airways [J]. Journal of Aerosol Medicine and Pulmonary Drug Delivery, 2009, 22(4): 341-353.

[10]LIU H, KANG Q, LEONARDI C R, et al. Multiphase lattice Boltzmann simulations for porous media applications [J/OL]. Computational Geosciences, 2015: 1-29. [2016-01-15]. doi: 10.1007/S10596-015-9542-3.

[11]王宁宁, 刘海湖, 张楚华. 基于格子Boltzmann方法的Rayleigh-Taylor两相不稳定流动研究 [J]. 工程热物理学报, 2016, 37(1): 89-94. WANG Ningning, LIU Haihu, ZHANG Chuhua. Numerical simulation of Rayleigh-Taylor instability based on lattice Boltzmann method [J]. Journal of Engineering Thermophysics, 2016, 37(1): 89-94.

[12]安红妍, 张楚华, 王宁宁. 基于格子Boltzmann方法的液液不混溶两相流动数值模拟 [J]. 工程热物理学报, 2014, 35(1): 78-81. AN Hongyan, ZHANG Chuhua, WANG Ningning. Numerical simulation of liquid-liquid two-phase flow based on lattice Boltzmann method [J]. Journal of Engineering Thermophysics, 2014, 35(1): 78-81.

[13]LIU H, VALOCCHI A J, ZHANG Y, et al. Lattice Boltzmann phase-field modeling of thermocapillary flows in a confined microchannel [J]. Journal of Computational Physics, 2014, 256: 334-356.

[14]QIAN Y, D’HUMIRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation [J]. Europhysics Letters, 1992, 17(6): 479.

[15]HU Y, BIAN S, FILOCHE M, et al. Flow and sound generation in human lungs: models of wheezes and crackles [M]. Neidelberg, Germany: Springer, 2014: 301-317.

(编辑 苗凌)

Numerical Simulation for Liquid Bridge Reopening Process with Two-Phase Lattice Boltzmann Method

WANG Ningning,LIU Haihu,ZHANG Chuhua

(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Based on the recently proposed and developed phase-field lattice Boltzmann method, a computational model is established to simulate the reopening process of blocked human pulmonary airway. The two-phase computational model is established following the free energy theory, and an order parameter is introduced for the description of two-phase interface, which evolves according to the Cahn-Hilliard equation. The model thus has a solid physical foundation. A pressure distribution function is utilized for the hydrodynamic equations, which facilitates minimizing the discretization error of the density gradient to weaken the numerical instability. In addition, an interfacial force of potential form is adopted, which produces much smaller spurious velocities at the interface by comparing with its counterpart of pressure form. The model is used to simulate the liquid bridge reopening process, and the effect of capillary number is analyzed. There exists a critical capillary number, beyond which the axial thickness of the liquid bridge decreases, and finally ruptures, leading to the reopening of blocked human pulmonary airway. Two kinds of reopening processes are reproduced, and they are classified by whether droplets are formed. The reopening process without droplet formed undergoes a more severe pressure jump. This approach is expected be used to further investigate physiology and pathology of human respiratory system and fundamental immiscible two-phase flow phenomenon in microchannels.

lattice Boltzmann method; two-phase flow; microchannel; interfacial force; liquid bridge reopening

2016-03-12。 作者简介:王宁宁(1989—),女,博士生;刘海湖(通信作者),男,特聘研究员。 基金项目:国家自然科学基金资助项目(51176146,51506168);中组部“千人计划”青年人才项目;西安交通大学青年拔尖人才支持计划。

时间:2016-06-14

10.7652/xjtuxb201609009

TK124

A

0253-987X(2016)09-0055-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160614.1717.006.html