考虑剪切变形影响的桩基m法计算理论

杨美良,罗婉庆,张建仁

(长沙理工大学 土木与建筑学院，长沙 410114)



考虑剪切变形影响的桩基m法计算理论

杨美良,罗婉庆,张建仁

(长沙理工大学 土木与建筑学院，长沙 410114)

考虑桩基的剪切变形影响，利用单广义位移深梁理论，建立了桩基m法的计算方法，导出了水平位移、转角、弯矩和剪力的初参数表达式和无量纲参数函数的统一表达式，根据桩底边界条件建立了初参数解的计算公式；给出了无量纲参数函数随换算深度和弯剪刚度比的变化图形。研究表明,换算深度小于3.0时，弯剪刚度比对无量纲参数函数影响较小，换算深度大于4.0时，弯剪刚度比对无量纲参数函数影响的趋势非常明显，桩基剪切变形的影响程度与桩的边界条件有关。算例结果表明，桩身的剪切变形有增大桩顶水平位移、提高弯矩零点位置、改变弯矩分布特征、扩大桩侧土压力大小等影响。

桩；单广义位移梁理论；剪切变形；初参数； m法

目前,考虑剪切变形影响的深梁有0～3阶剪切变形理论，被广泛认同的理论有Timoshenko理论[6]、Jemielita理论[7]、Levinson理论[8]、Bickford理论[9]、Reddy理论[10]等，这些理论都有2个或以上的位移，计算上不方便。2000年，龚克提出了单广义位移深梁理论[11]，该理论能用单一的广义挠度表出转角、弯矩和剪力，计算上非常方便，本文选择该理论来建立桩基m法分析方法，以考虑基桩的剪切变形影响，推动桩基计算理论的发展。

1 单广义位移深梁理论

2000年龚克提出单广义位移深梁理论，建立理论模型时取梁的中心线为x轴，梁的挠曲面为xy平面, 对梁的变形作如下假设[11]：1)梁的中性轴的轴向位移不计，y方向的挤压变形不计；2)变形前垂直于中心线的平面在变形后仍保持为平面(不一定垂直于挠曲线) ；3)剪切转角随x二阶变化率不计。相应的平衡方程、转角ψ、弯矩M和剪力Q表达式如下[13]见式(1)。

(1)

式中：D(=EI)为桩身的抗弯劲度、C(=kGA)为桩身的抗剪劲度、k为桩身截面的剪切修正系数，圆形截面取9/10、矩形截面取5/6。

从以上计算公式可以看出，单广义位移深梁理论的平衡方程与Euler梁理论一致，转角、弯矩和剪力用广义位移挠度表示，该理论的正确性和推广应用已在文献[11]中有充分论证。

2 弹性桩的m法计算理论

采用弹性桩m法的计算假定，弹性桩侧受水平分布力的平衡条件为

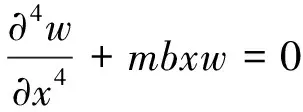
(2)

α5·x·w

(3)

设桩侧水平位移解为级数解，如式(4)所示。

a0+a1x+a2x2+…+anxn+…

(4)

将式(4)求导，其第一、二、三、四阶导数为

·i·xi-1

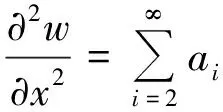
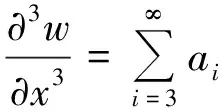
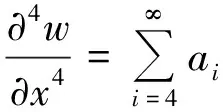
(5)

将式(4)、(5)代入式(3)，并展开，使等式恒成立，则应有a4=0，除a4=0外，其他系数应满足关系式

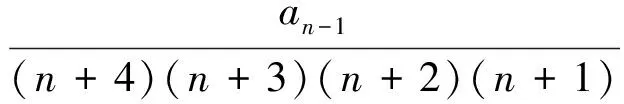
(6)

式中：n=1,2,3,…,∞。

进一步分析，可知

a5k-1=0,k=1,2,3,…

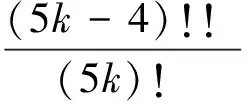
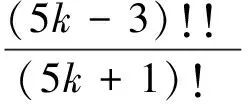
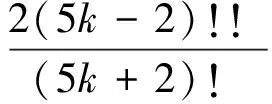
(7)

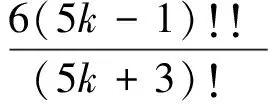
式中：()!!符号含义式(8)所示。

(5k-T)!!=

[5k-T][5(k-1)-T][5(k-2)-T]…

[5·2-T][5·1-T]

(8)

将各系数表达式等代入位移解，有

w(x)=a0·Y0(x)+a1·Y1(x)+

a2·Y2(x)+a3·Y3(x)

(9)

式中：

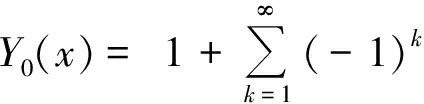
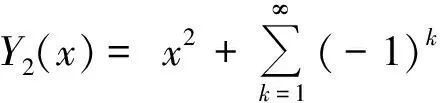
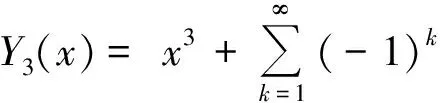
当x=0时，假定桩顶的位移、转角、弯矩和剪力代入式(9)，可确定参数a0、a1、a2、a3。由式(1)的第2、3、4式可知，桩的转角、弯和剪力用广义位移表示为

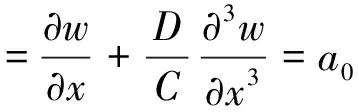
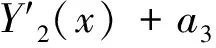
a1·Y‴1(x)+a2·Y‴2(x)+a3·Y‴3(x)]

Da0·Y″0(x)+a1·Y″1(x)+a2·Y″2(x)+

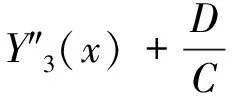
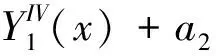
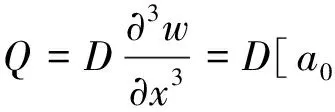
a2·Y‴2(x)+a3·Y‴3(x)]

(10)

当x=0时，有

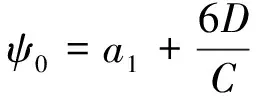
M0=2D·a2,Q0=6D·a3

(11)

解得

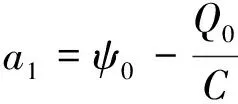
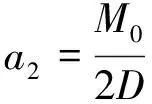
(12)

用x=0时的初参数表示的位移、转角、弯矩和剪力为

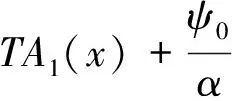
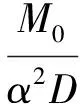
(13)

式中：

(14)

式中：EA1(x),EB1(x),EC1(x),ED1(x)为不考虑剪切变形影响时基于Euler梁理论的对应无量纲参数函数，具体表达式为[2]

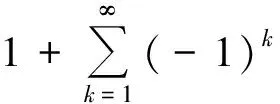
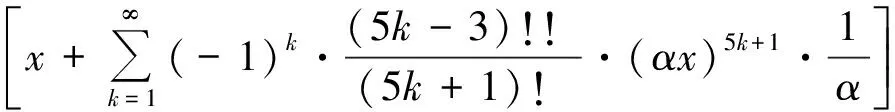
(15)

转角表达式为

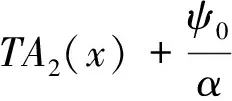
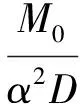
(16)

式中：

·EA4(x)

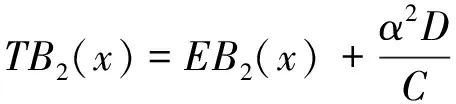
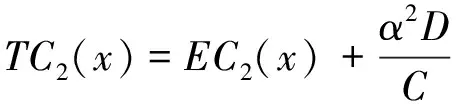
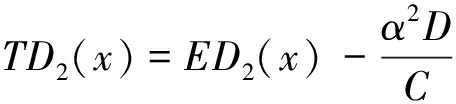
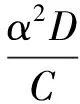
(17)

式中：EA2(x),EB2(x),EC2(x),ED2(x)为不考虑剪切变形影响时基于Euler梁理论的对应无量纲参数函数，分别由EA1(x),EB1(x),EC1(x),ED1(x)求一次导数后再除以α得到。

弯矩表达式为

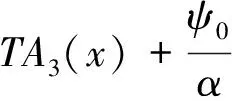
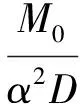
(18)

式中：

·EA5(x)

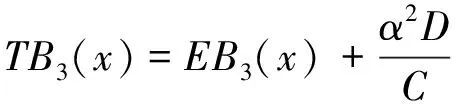
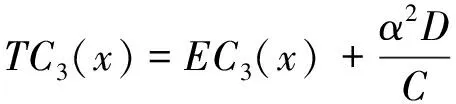
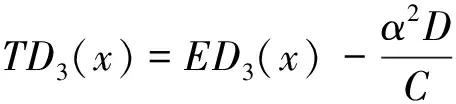
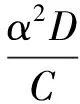
(19)

式中：EA3(x)、EB3(x)、EC3(x)、ED3(x)和EA5(x)、EB5(x)、EC5(x)、ED5(x)为不考虑剪切变形影响时基于Euler梁理论的对应无量纲参数函数，分别是由EA2(x)、EB2(x)、EC2(x)、ED2(x)和EA4(x)、EB4(x)、EC4(x)、ED4(x)求一次导数后再除以α得到。

剪力表达式为

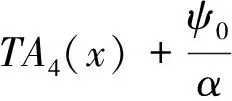
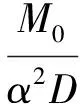
(20)

式中：

(21)

EA4(x)、EB4(x)、EC4(x)、ED4(x)为不考虑剪切变形影响时基于Euler梁理论的对应无量纲参数函数，分别是由EA3(x)、EB3(x)、EC3(x)、ED3(x)求一次导数后再除以α得到。

从以上所推导的计算公式可以看出，正是由于单广义位移深梁理论具有位移、转角、弯矩和剪力都可用单广义位移来表示的特点，使得考虑剪切变形影响的桩基m法分析仍可用级数来求解。如果采用经典的Timoshenko深梁理论来考虑剪切变形的影响，其级数解非常复杂。可以这样说，选用单广义位移深梁理论是建立考虑剪切变形影响的桩基m法分析模型的最成功技巧。

3 计算公式的统一表达

从上述计算公式可以看出，考虑剪切变形的计算函数EAi(x)、EBi(x)、ECi(x)、EDi(x)(i=1、2、3、4、5)都可由不考虑剪切变形的无量纲参数函数表示，而不考虑剪切变形影响的计算函数可用一种统一的公式来表达[12]。即

AA(i,j)=S(i,j)·(αx)j-i+

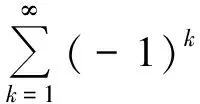
(22)

式中：i=1、2、3、4、5代表上式中挠度、转角、弯矩、剪力及补充项的计算，j=1、2、3、4代表各计算公式中的A、B、C、D。其中的S(i,j)表达式如式(23)。

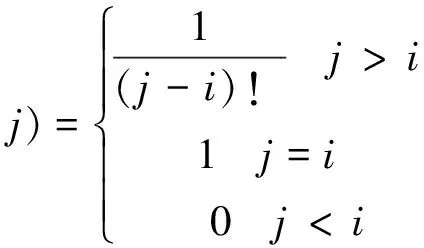
(23)

式(23)中，级数收敛很快，一般取前10项就有很高的计算精度，甚至取前5项即可。

4 边界条件的处理及桩顶位移的确定

4.1 摩擦桩、柱承桩w0、ψ0的计算

当摩擦桩的αh≥2.5、柱承桩的αh≥3.5时，桩底转角很小，可以忽略[2]，相应的桩顶位移、转角用桩顶弯矩、剪力表示为

(24)

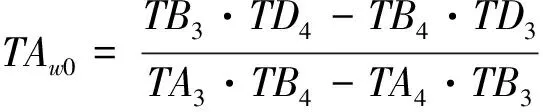
4.2 嵌岩桩w0、ψ0的计算

嵌岩桩桩底固结，据此条件可求出桩顶位移、转角用桩顶弯矩、剪力表示为

(25)

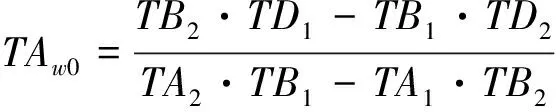
5 无量纲参数函数

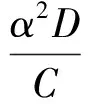
(26)

改变桩的弯剪刚度比R和换算深度αh，各无量纲参数函数随R、αh的变化如下图1所示。计算中R取0、0.1、0.125、0.15、0.175、0.20、0.22、0.23、0.24。当R=0时，表示抗剪劲度无穷大，即为不考虑桩的剪切变形影响的计算结果。

图1 桩身位移和内力的计算参数函数随换算深度αh和弯剪刚度比R的变化Fig. 1 Calculating parameter functions of inner displacements and forces changing

从图1可以看出，当换算深度αh<3.0时，弯剪刚度比R对无量纲参数函数的影响较小；只有当αh>3.0后，弯剪刚度比R对无量纲参数函数的影响才开始显示出来；在αh>4.0后，弯剪刚度比R对无量纲参数函数的影响的趋势非常明显。

根据式(24)，摩擦桩或柱承桩的计算参数随弯剪刚度比R、换算深度αh的变化如图2所示。计算中R取0、0.02、0.04、0.06、0.08、0.10、0.12、0.14、0.16、0.18、0.20、0.24。

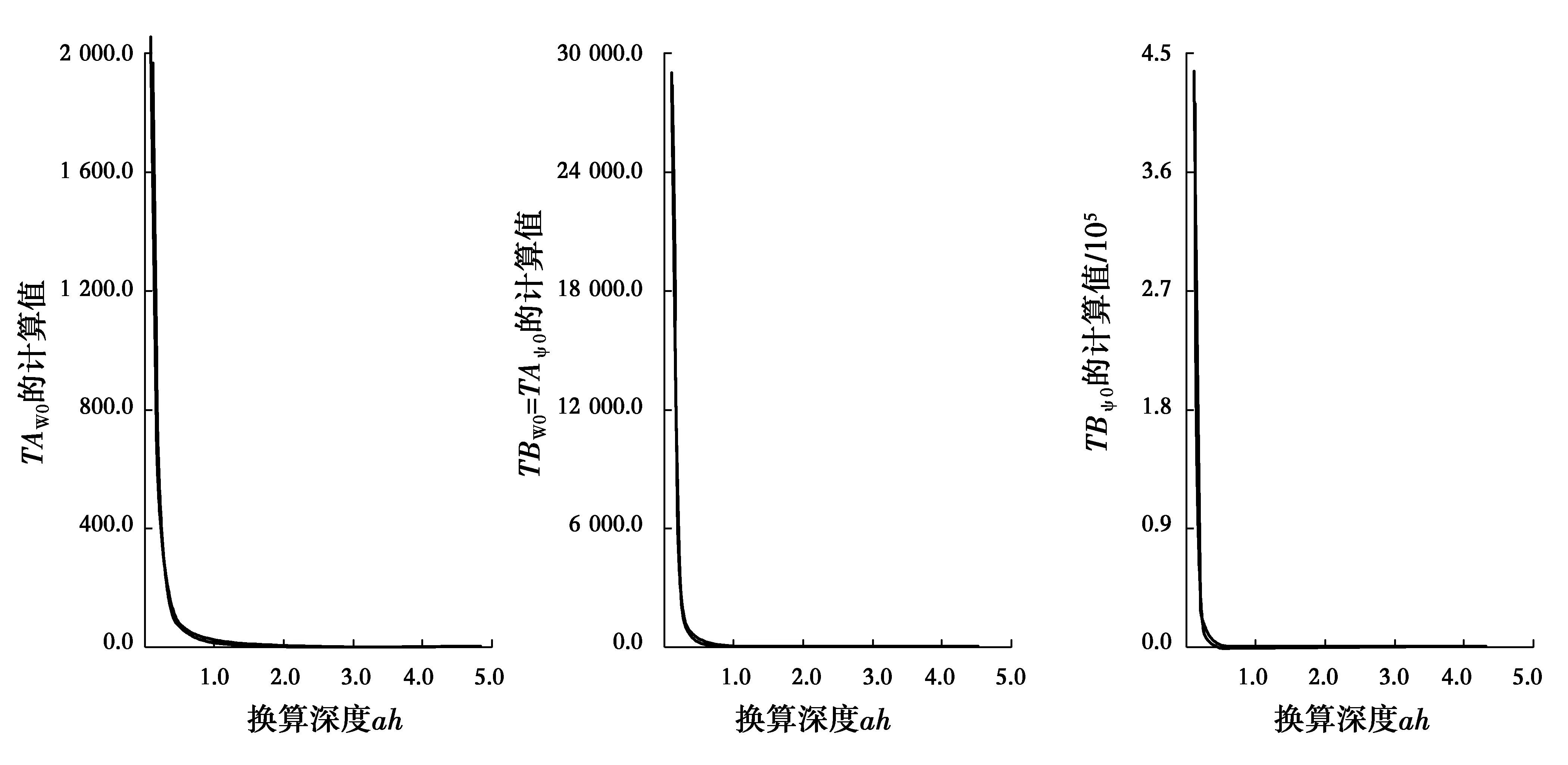
图2 摩擦桩或支承桩的计算参数随换算深度αh和弯剪刚度比R的变化Fig.2 Calculating parameters of inner displacements and forces changing

从图2 可以看出，弯剪刚度比R对摩擦桩、支承桩的计算参数的影响非常小，在图中由于分辨的原因基本看不出来。其与不考虑剪切变形时(R=0)的相应参数基本一致。因此对于摩擦桩、支承桩，可以不考虑剪切变形的影响。

根据式(25)，嵌岩桩的计算参数函数随弯剪刚度比R、换算深度αh的变化如图3所示。计算中R取0～3.6。从图3可以看出，当换算深度αh<3.0时，弯剪刚度比对嵌岩桩的计算参数影响较大、而在αh>3.0后，其影响则比较小。因此，剪切变形对桩基的影响与其边界条件有关。

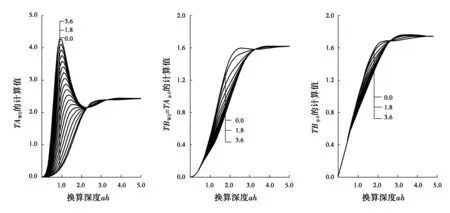
图3 嵌岩桩的计算参数函数随换算深度αh和弯剪刚度比R的变化Fig. 3 Calculating parameter functions of inner displacements andf forces changing with converting length and ratio bending stiffness to shear stffness

6 计算示例

已知一桩基，弹性模量E=2.6×107kPa、桩径r=1.65 m、计算宽度b=0.9(r+1)=2.385 m、抗弯刚度折减系数0.67，桩身抗弯刚度实际取值为D=0.67EI=6.338×106kN·m2、抗剪刚度C=kGA=2.085×106kN，桩长10 m，边界条件为嵌岩桩，按式(25)计算桩顶的变形参数。桩顶作用的水平剪力Q0=35.70 kN、弯矩M0=684.70 kN·m。计算时桩的变形系数α=0.327 39。人为改变弯剪刚度比R，桩身水平变形、弯矩、桩侧土水平压力随桩长的变化如图4～6所示。

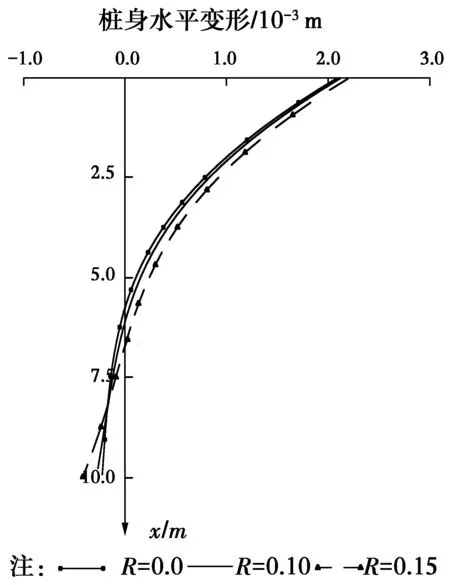
图4 桩身水平变形分布图Fig.4 Horizontal displacement

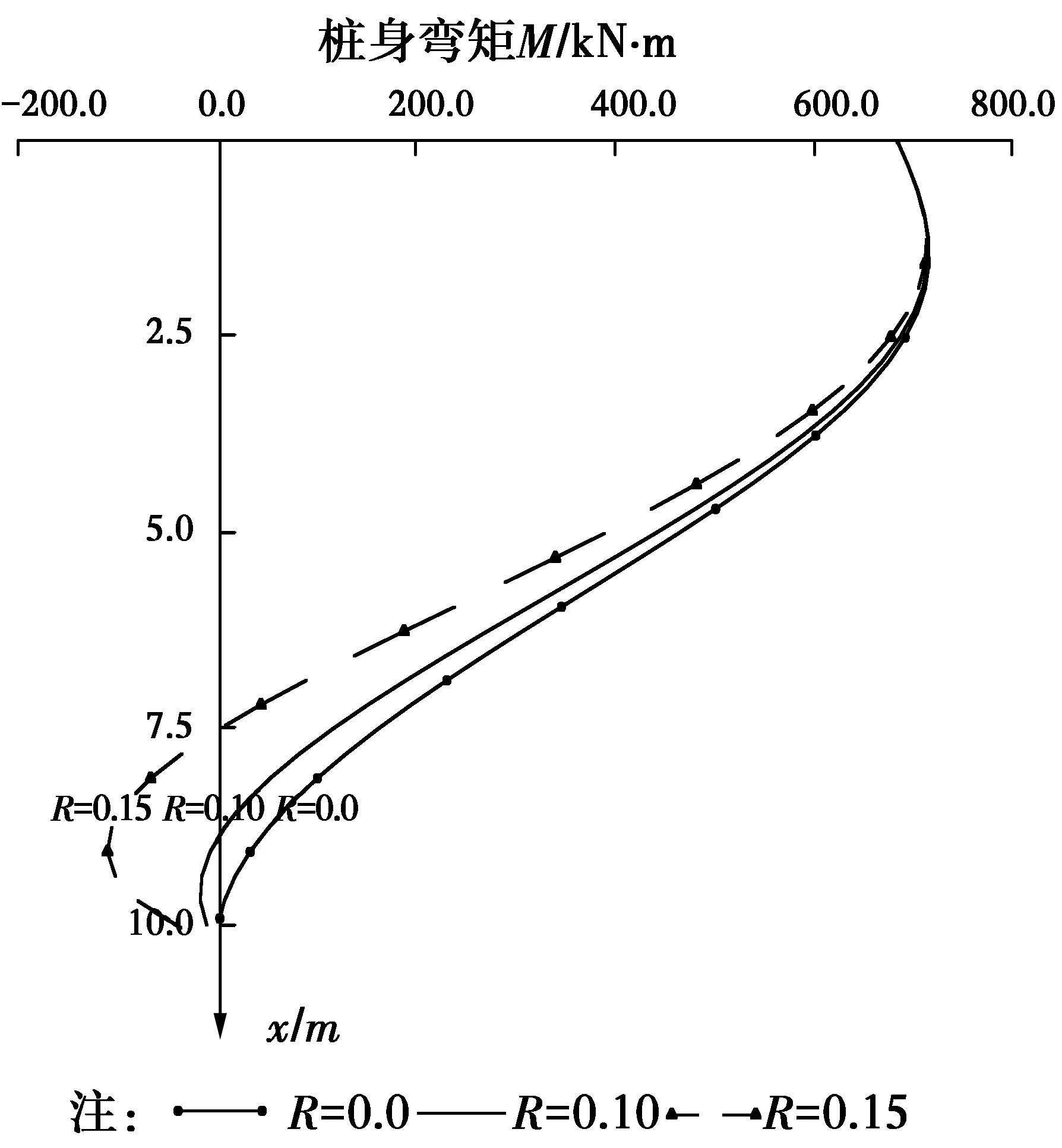
图5 桩身弯矩分布图Fig.

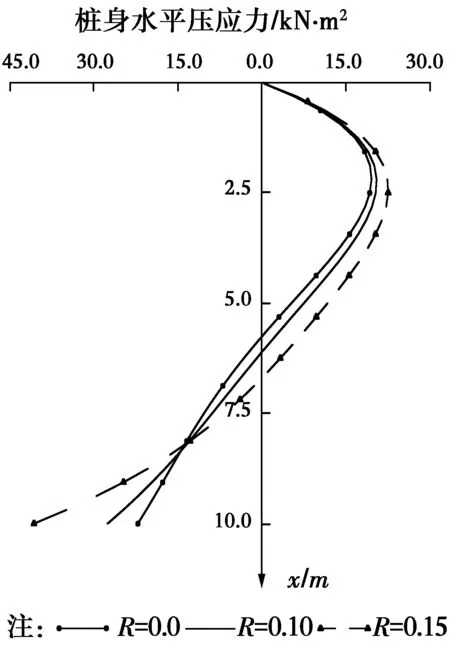
图6 桩侧土水平压力分布图Fig.6 Horizontal stress

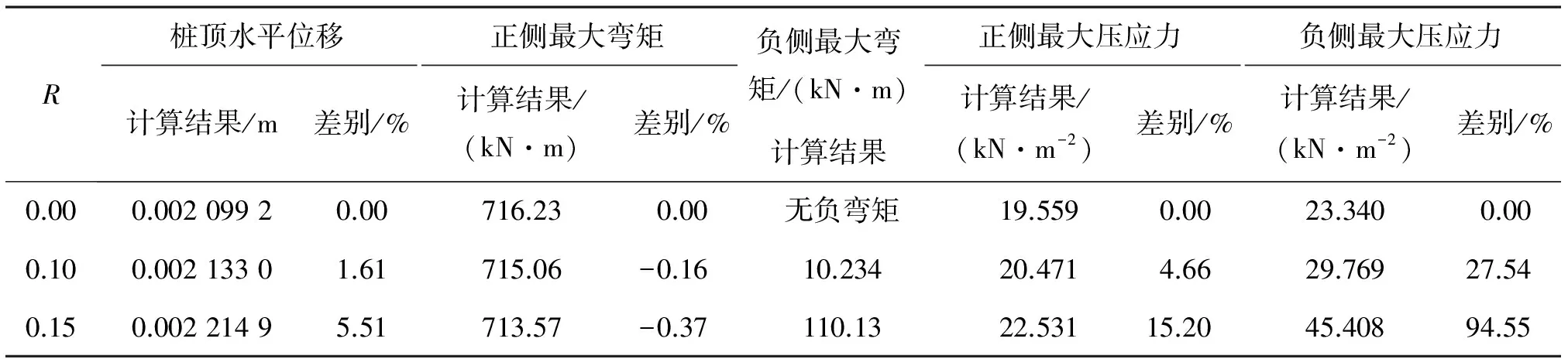
Table 1 Comparing of calculating results

R桩顶水平位移计算结果/m差别/%正侧最大弯矩计算结果/(kN·m)差别/%负侧最大弯矩/(kN·m)计算结果正侧最大压应力计算结果/(kN·m-2)差别/%负侧最大压应力计算结果/(kN·m-2)差别/%0．000．00209920．00716．230．00无负弯矩19．5590．0023．3400．000．100．00213301．61715．06-0．1610．23420．4714．6629．76927．540．150．00221495．51713．57-0．37110．1322．53115．2045．40894．55

从图4和表1的桩顶水平位移数据栏可以看出，随着R的加大，桩的抗剪刚度减小，桩顶水平位移加大。当R=0.15时，桩顶水平位移与不考虑剪切变形的位移大5.51%。

从图4和表2的正侧最大弯矩、负侧最大弯矩数据栏可以看出，考虑剪切变形影响时，桩侧最大正弯矩减小、负侧最大弯矩增大。本算例中，不考虑剪切变形时，桩身长度范围内不出现负弯矩，但考虑剪切变形后，由于桩身的弯曲刚度减小，桩身变形加大，正侧弯矩与不考虑剪切变形影响时的结果减小0.37%，同时，在另一侧出现负弯矩现象，不考虑剪切变形影响时则无负弯矩出现。因此，剪切变形对桩身的弯矩分布有一定影响，并有提高弯矩0点位置的作用。

从图5和表2的正侧最大压应力和负侧的最大压应力数据栏可以看出，考虑剪切变形的影响后，正、负侧的最大压应力都有所扩大，其中，正侧正应力与不考虑剪切变形时的结果扩大15.20%、负侧正应力扩大94.55%。

7 结论

从以上的分析、公式推导和算例分析可以看出：

1)本文精心选择单广义位移深梁理论，建立桩基m法分析方法，可以考虑桩身剪切变形影响，当弯剪刚度比为0时可退化成不考虑剪切变形影响的形式，因此，所导出计算公式的适应性比目前基于Euler梁理论的常用m法更好。

2)不考虑边界条件时，桩身位移、内力计算的无量纲参数函数有统一表达式，计算时取级数的前10项就有非常高的精度。

3)当换算深度αh>3.0时，剪切变形对位移、内力计算的无量纲参数函数的影响才开始显示出来，当换算深度αh<3.0时剪切变形影响甚小。

4)随着弯剪刚度比的增大，剪切变形有扩大桩顶位移、减小桩身正弯矩、改变桩身两侧弯矩的分布特征、提高弯矩0点位置等作用。

[1] 吴恒立.计算推力桩的综合刚度原理和双参数法[M].北京:人民交通出版社,2000:1-38. WU H L. Synthetical stiffness principle and biparameter method for lateral loaded piles[M].Beijing: China Communications Press,2000:1-38.(in Chinese)

[2] 凌治平.基础工程[M].北京:人民交通出版社,1986:96-114. LIN Z P. Foundation engineering[M]. Beijing: China Communications Press,1986:96-114.(in Chinese)

[3] 夏桂云.嵌岩弹性桩的稳定分析[J].重庆交通学院学报,2001,20(1):79-82. XIA G Y. Stability analysis of socketed poles[J]. Journal of Chongqing Communications University,2001,20(1):79-82.(in Chinese)

[4] 戴自航,陈林靖.多层地基中水平荷载桩计算m法的两种数值解析[J].岩土工程学报,2007,29(5):690-696. DAI Z H,CHEN L J. Two numerical solutions of laterally loaded piles installed in multi-layered soils by m method[J].Chinese Journal of Geotechnical Engineering, 2007, 29(5):690-696.(in Chinese)

[5] 肖世卫.横向受力桩中剪切变形影响的分析[J].西南交通大学学报,1992(1):28-31. XIA S W. Analysis of the influence of shear deformation on laterally loaded piles[J]. Journal of Southwest Jiaotong University,1992(1):28-31.(in Chinese)

[6] 夏桂云,李传习.考虑剪切变形影响的杆系结构理论与应用[M].北京:人民交通出版社,2008. XIA G Y,LI C X. Calculating theory and its applications of frame structures with shear deformation effects[M].Beijing:China Communications Press,2008.(in Chinese)

[7] WANG C M， REDDY J N， LEE K H. Shear deformable beams and plates[M]. Amsterdam:Elsevier, 2000.

[8] LEVINSON M. A new rectangular beam theory [J]. Journal of Sound and Vibration,1981(74):81-87.

[9] BRICKFORD W B. A consistent higher order beam theory [J]. Developments in Theoretical and Applied Mechanics,1982(11):137-150.

[10] REDDY J N. A simple higher order theory for laminated composite plates[J]. Journal of Applied Mechanics,1984(51):745-752.

[11] 龚克.单广义位移的深梁理论与中厚板理论[J].应用数学和力学,2000,21(9):984-990. GONG K. Bending Theories for beams and plates with single generalized displacement[J]. Applied Mathematics and Mechanics,2000, 21(9):984-990.(in Chinese)

[12] 周相略.桩基础m法计算系数的统一表达式[J].公路,1993(6):18-22. ZHOU X N. Uniform expressions for calculating parameters of piles by m method[J]. Highway,1993(6):18-22.(in Chinese)

(编辑 胡玲)

Calculating theory of m method assumption for piles with shear deformation effect

YangMeiliang，LuoWanqing，ZhangJianren

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410114, P.R. China)

Considering the shear deformation effect of piles, the calculating theory of m method assumption for piles was presented by using the single generalized displacement theory of deep beam. The initial parameter formulae to horizontal displacement, slope, moment and shear force were derived. The unified non-dimensional functions were also put forward. According to the boundary conditions, the initial parameters solutions were determined. The changing figures of non-dimensional functions with converting length and ratio of bend stiffness to shear stiffness were plotted. Some conclusions were summarized that when the converting length was less than 3.0, there was little influence of the ratio of bending stiffness to shear stiffness on the non-dimensional functions , while the converting length was greater than 3.0, the influence of the ratio of bending stiffness to shear stiffness on the non-dimensional functions became obvious; the influencing degree of the shear deformation effect was related to the boundary conditions. Example results showed that shear deformation can enlarge the horizontal displacement at the top, lift the position of zero moment, change moment distribution and magnify the soil pressure on pile.

pile; single generalized displacement beam theory; shear deformation; initial parameter; m method

2016-04-08

国家自然科学基金(51278072)；湖南交通科技创新项目(201452)

杨美良(1967-)，女，教授，博士，主要从事桥梁结构理论分析,(E-mail)yangmeiliang@163.com。

Foundation item：National Natural Science Foundation of China(No.51278072)；Communication Science and Technology Innovation Project of Hunan(No.201452)

10.11835/j.issn.1674-4764.2016.06.008

TU473

A

1674-4764(2016)06-0054-08

Received:2016-04-08

Author brief：Yang Meiliang(1967-)，professor，PhD, main research interest：theoretical analysis of bridge structure,(E-mail)yangmeiliang@163.com.