大型地下洞室开挖爆破破坏影响范围

陈俊桦，张家生，李新平



大型地下洞室开挖爆破破坏影响范围

陈俊桦1，张家生1，李新平2

(1. 中南大学土木工程学院，湖南长沙，410075；2. 武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北武汉，430070)

大型地下洞室爆破开挖通常需要考虑岩体完整程度的影响。以位于四川和云南交界的金沙江上的溪洛渡水电站特大断面地下主厂房浅孔台阶开挖爆破工程为研究背景，提出考虑初始损伤影响的岩石爆破损伤模型以及和初始损伤相关且可用于确定爆破破坏影响范围的判据。建立初始损伤和岩体完整性指数之间的关系式，使得提出的本构模型能考虑岩体完整程度的影响。通过编程将提出的本构模型应用到FLAC3D软件中，进行爆破数值模拟。首先分析岩石爆破破坏影响范围特性，然后以爆破破坏最大水平半径作为爆破破坏影响范围的特征参数，分析爆破破坏最大水平半径和岩石初始损伤、单段爆破药量以及爆破质点峰值振动速度之间的关系，得到不同初始损伤条件下爆破破坏对应的临界振动速度和安全允许炸药量。最后利用现场爆破试验、钻孔声波测试和质点峰值振动速度测试的结果验证数值模拟结果的合理性。研究结果表明：对于浅孔台阶爆破，水平径向爆破破坏影响范围随孔深的减小而增加，并在顶部平面达到最大值。该破坏边缘质点的峰值振动速度可作为爆破施工监测的安全判据。岩石初始损伤越大，初始损伤对爆破破坏最大水平半径的影响越显著。数值计算结果和现场试验结果较吻合。

岩石力学；水电站地下厂房；爆破安全判据；爆破数值模拟；质点峰值振动速度；岩体完整程度

地下开挖洞室按照开挖断面尺寸可划分为小断面、中断面、大断面和特大断面4种类型，其中大—特大断面洞室一般称作大型地下洞室。在我国水利水电、矿山、铁路等行业中，大型地下洞室开挖项目蓬勃开展。如对于水利水电行业，我国在金沙江下游流域开发建设溪洛渡、向家坝、乌东德、白鹤滩这4座巨型水电站。这些水电站地下洞室开挖工程主要由大型地下洞室群构成。与一般的中小型地下开挖工程不同，大型地下洞室的开挖断面积大，爆破安全问题更突出。如溪洛渡主厂房的最大开挖高度约为80 m，最大开挖宽度约为30 m。即便采用了分层开挖以及毫秒雷管分段起爆等方式降低爆破影响，但是受到经济成本和开挖技术等因素限制，在实际工程中这种分层的高度和雷管的分段数都是有限的，故爆破强度的降低也总是有限的，即爆破影响不可避免。因此，大型地下洞室开挖工程通常要求对开挖过程中的爆破破坏影响范围进行安全评估。爆破破坏影响区域一般可划分为爆炸近区和爆炸中远区。爆炸近区围岩裂纹的破裂扩展及其影响范围和爆炸中远区围岩的爆破振动效应是研究热点。大型地下洞室开挖工程特别是大型水电站地下开挖工程通常对围岩质量要求较高，这需要施工中尽量降低爆炸近区围岩的爆破破裂范围或者破裂深度。对于一些特别重要的构筑物如水电站主厂房内的岩台等，甚至要求无爆破破坏影响。因此，大型地下洞室开挖工程更为关注爆炸近区的破坏影响范围，即大型地下洞室开挖爆破破坏影响范围通常指的是爆炸近区围岩的破裂范围。根据损伤理论，该范围一般也称作爆破损伤影响范围。研究围岩爆破破坏影响范围的方法主要有现场试验和数值模拟试验，这2种方法常结合在一起使用。现场试验主要包括岩体声波测试和爆破振动测试。由于岩石力学性质复杂，对于多数通用数值计算程序如LS-DYNA，ABAQUS和FLAC3D等，一般需通过编程的方式将合适的岩石本构模型应用到数值计算程序中。目前最常用的本构模型为爆破损伤模型。AHRENS等[1−2]认为岩石声波波速降低能反映出其力学性质的损伤劣化。据此，严鹏等[3−4]在现场利用钻孔声波测试研究洞室开挖损伤区特性，以此评估爆破破坏影响范围。卢文波等[5−6]认为峰值振动速度可作为岩石爆破损伤判据或安全判据。张国华等[7−8]通过编程将爆破损伤本构模型应用于LS-DYNA和UDEC等软件中，进行数值模拟，并结合现场声波测试研究爆破破坏影响范围。李新平等[9]在FLAC3D程序中编制爆破损伤本构关系，通过爆破数值模拟分析破坏范围与单段爆破药量之间的关系，并提出了判定爆破损伤范围的峰值振动速度判据。由以上可知，不少学者利用爆破损伤理论研究爆破破坏影响范围，并将爆破破坏判定与工程中常用的监测手段联系起来，方便工程应用。但是，目前能考虑岩石初始损伤影响的爆破损伤模型很少，而天然岩石一般是含缺陷的损伤材料。岩石细观初始损伤在宏观上影响岩体的完整程度。对于大型地下洞室开挖工程，通常情况下，施工区内岩石种类一般较为单一，岩石强度变化不大，岩石初始损伤或者岩体完整程度的离散程度可能较大。在该情况下，现有爆破损伤模型的应用受到了制约。溪洛渡水电站主厂房为特大断面的大型地下洞室。洞室围岩的主要特点为岩石强度变化不大，大部分围岩完整程度较好，小部分的完整程度较差。本文以主厂房第Ⅲ层中部台阶浅孔爆破开挖为研究背景，根据岩石爆破损伤相关理论建立考虑岩石初始损伤影响的本构模型，将岩石初始损伤与岩体完整程度联系起来，进行爆破数值模拟。同时结合现场爆破试验、爆破振动速度测试和钻孔声波试验共同研究爆破破坏影响范围特性及安全判据，以期研究成果为类似的大型地下开挖工程爆破安全控制等提供参考。

1 工程背景

溪洛渡水电站是1座位于金沙江下游的大型水电站，左、右岸各相应布置大型地下厂房洞室群，其主要构(建)筑物均位于坚硬的玄武岩中。完整岩石的单轴饱和抗压和抗拉强度可分别达100 MPa和10 MPa。左岸地下厂区水平埋深300~450 m，垂直埋深340~ 480 m。左岸主厂房出露围岩主要为Ⅱ类，少数为Ⅲ类。岩体完整程度描述主要为较完整和完整性差。岩锚梁岩台是主厂房中高安全等级的构(建)筑物，为爆破安全控制的关键部位。水电站要求周边开挖爆破施工对岩台无破坏影响。岩锚梁所在部位埋深近400 m，垂直应力、水平应力和岩石抗拉强度数量级相同。这给爆破设计和施工带来了难度：一方面，为了减小岩石的夹制作用，需要增大爆破药量或扩大炮孔孔径；另一方面，为了减小爆破对围岩的破坏作用，需减少炸药装药量。因此，爆破安全问题突出。主厂房第Ⅰ~Ⅲ层爆破开挖分层示意图见图1。

图1中，第Ⅰ层采用导洞扩挖的开挖方式，第Ⅱ~Ⅲ层采用大孔径浅孔台阶爆破开挖方式，第Ⅲ层由第Ⅲ1层和第Ⅲ2层组成。保护层紧邻两侧边墙对称分布于主厂房内，其厚度设计值为4.00~5.75 m。第Ⅲ2层的保护层厚度设计值小于第Ⅲ1层厚度设计值，分层高度则比第Ⅱ层的大，爆破安全问题更突出。本文选取第Ⅲ2层的浅孔台阶开挖爆破为研究对象。为降低爆破强度，应减少同段起爆的炮孔数。考虑到产生应力波叠加效应的最小炮孔单元数为2个，设置单段同时起爆的炮孔数为2个。主要爆破参数设计为：采用毫秒雷管分段延时，2个炮孔同时起爆；现场布孔方式为矩形布孔。孔距为2.0 m，排距为1.8 m；钻孔直径为90 mm，钻孔深超过分层高度0.5 m。钻孔布置示意图如图1所示。药卷为柱状乳化炸药，药卷直径为70 mm，单孔炸药量根据岩体完整程度调整。对于较完整的岩体，单孔炸药量为9.00 kg；对于完整性差的岩体，单孔炸药量为6.75 kg。

数据单位：m

2 岩石爆破损伤理论模型

2.1 岩石爆破损伤本构关系

2.1.1 损伤演化规律

在爆炸荷载作用下，岩石的破坏主要表现为内部裂纹扩展。裂纹扩展过程是随机的但具备统计规律，即岩石损伤可用概率分布描述[10]。假定岩石细观单元的破坏是各向同性的，即岩石损伤为各向同性，根据强度统计理论，岩石损伤演化方程为[11]

式中：为损伤变量，0≤≤1；d为岩石细观单元裂纹密度。与d均为标量。

假设裂纹密度d是初始裂纹密度和动力作用激活的裂纹密度之和。考虑初始损伤影响时，岩石细观单元裂纹密度计算为[11−12]

(3)

式中：3和4为材料参数。

损伤变量和体积模量、剪切模量的关系分别为：

(6)

2.1.2 本构关系

有效应力和损伤变量的关系如下[13]：

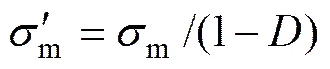
(8)

(10)

(11)

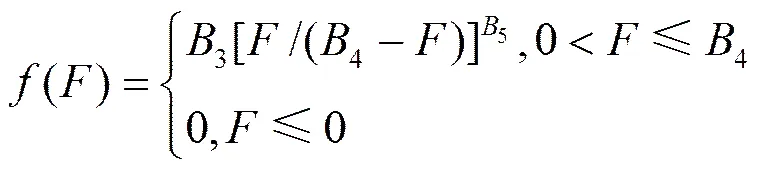
(13)

2.2 炮孔内边界上爆破冲击荷载计算模型

炮孔内炸药起爆并激发爆轰波的过程极其复杂。LS-DYNA等数值软件中常使用JWL方程作为爆轰产物状态方程[11−12, 14−15]，但该方程需测定的参数较多。为方便应用，根据C−J爆轰理论，假定爆轰波波阵面通过炸药后化学反应瞬时完成并生成爆轰产物。对于浅孔台阶爆破，由于爆轰波传播速度较快且孔深较小，可以忽略起爆位置的影响，近似认为炮孔中炸药爆炸是瞬时并定容完成的。瞬时爆轰平均压力为[9, 16]

现场采用径向不耦合、轴向连续装药方式。对于不耦合装药，不耦合装药系数较小(一般小于1.5)时，空气冲击波强度相对小且其衰减快，可以忽略。这样，炮孔内加载边界上爆炸荷载峰值压力由爆轰产物高压膨胀作用决定。该峰值压力计算如下：

图2 炮孔内爆炸荷载加载示意图

Fig. 2 Schematic plot of blast load on blasthole

孔内爆炸冲击荷载表达式为[17]

式中：为任意时刻孔内加载边界上单位面积爆炸压力；；0为初始损伤岩石的声波波速，即爆破开挖前的声波波速；和为与阻尼相关的量纲一计算参数；为加载时间。

2.3 基于爆破损伤理论的破坏判据

2.3.1 基于声波波速的损伤破坏判据

岩石损伤和声波波速的关系为[2]

若将宏观岩体结构的不完整看作由细观岩石单元的损伤演化导致，则岩石细观单元初始损伤的宏观表现则为初始状态(爆破开挖前)下的岩体完整程度。再考虑到岩体完整程度由岩体完整性指数定量划分，由式(18)得到岩石初始损伤与岩体完整性指数间的关系为

由式(13)，(14)和(19)，本文提出的本构模型可以考虑岩体完整程度的影响。

根据DL/T 5389—2007“水工建筑物岩石基础开挖工程施工技术规范”，采用钻孔声波法评价爆破对岩体的影响。当声波波速下降为爆破前初始波速的15%时，可判定岩体内出现爆生裂隙或受爆破破坏的影响。根据式(18)~(19)，与爆破破坏范围边缘对应的爆破损伤门槛值为

根据量纲分析和爆炸几何相似律，爆破破坏影响范围与炸药量、声波波速等参数之间的关系为

2.3.2 基于质点峰值振动速度的损伤破坏判据

临界质点峰值振动速度计算为

式中：lim为与对应的临界爆破振动速度，方向指向爆炸几何中心；和为材料参数。

3 爆破数值模拟试验和现场爆破试验

3.1 试验方案

试验分为爆破数值模拟试验和现场爆破试验，通过现场试验可验证数值模拟的合理性。从图1可知：对保护层的破坏影响主要由靠近保护层的炮孔爆破引起；当采用雷管分段延时起爆时，爆破破坏影响范围主要由单段同时起爆的炮孔引起。因此，结合现场实际情况，数值模拟的炮孔单元数设置为2个，且2个炮孔装药参数相同。影响岩石动力响应的主要内部因素为岩石初始损伤，外部影响因素主要为炸药装药量。水工隧洞围岩分类依据主要为岩石强度、岩体完整性指数和结构面产状等。主厂房基岩质量较好，影响岩体质量的主要指标为岩体完整性指数。由于主厂房岩体完整性描述主要为较完整和完整性差，根据GB 50487—2008“水利水电工程地质勘察规范”，主厂房内岩体的完整性指数范围V分别为(0.55，0.75]和(0.35，0.55]，在此范围内选取数值作为试验控制条件。由式(19)可将岩体完整性指数与岩石初始损伤相联系。

3.1.1 数值模拟试验条件

岩体完整性指数V范围为[0.35，0.75]，岩石初始损伤0范围为[0.25，0.65]，岩石爆破损伤门槛值lim范围为[0.46，0.75]。考虑到现场炮孔堵塞长度一般大于最小抵抗线，结合炸药包的几何规格，单孔炸药量e取值范围为[6.75，10.00]，单位为kg。

3.1.2 现场试验条件

岩体完整性指数V=0.7，岩石初始损伤0=0.3，岩石爆破损伤门槛值lim=0.5，单孔炸药量取值e= 9.0 kg，单段爆破炸药量为p=18.0 kg。

现场试验包括爆破试验、钻孔声波测试和爆破振动速度测试。钻孔声波测试目的是测定爆炸近区的破坏影响范围，爆破振动速度测试目的是测定爆炸地震波衰减规律。声波孔的孔间距为1.0 m或0.5 m，孔半径为30.0 mm或45.0 mm，声波孔深为4.0 m或8.0 m。声波测试仪器为岩海RS-ST01C超声波检测仪，爆破振动速度测试仪为TOPBOX测振仪。声波测试时，沿孔深方向测定声波波速变化，根据式(18)~(20)判定临界损伤点。临界损伤等值线包络的范围为爆破破坏影响范围。当某一测点沿孔长的损伤值均小于损伤门槛值时，在该测点附近新增声波测试孔，以便使爆破破坏影响范围的判定更精确。在起爆后的原有炮孔位置或附近布置约5.0 m深的垂直孔，用于测试孔底的爆破破坏影响范围。爆破振动速度的测点监测方向为垂直向和水平径向，水平径向指向爆心。现场试验测点布置示意图见图3。

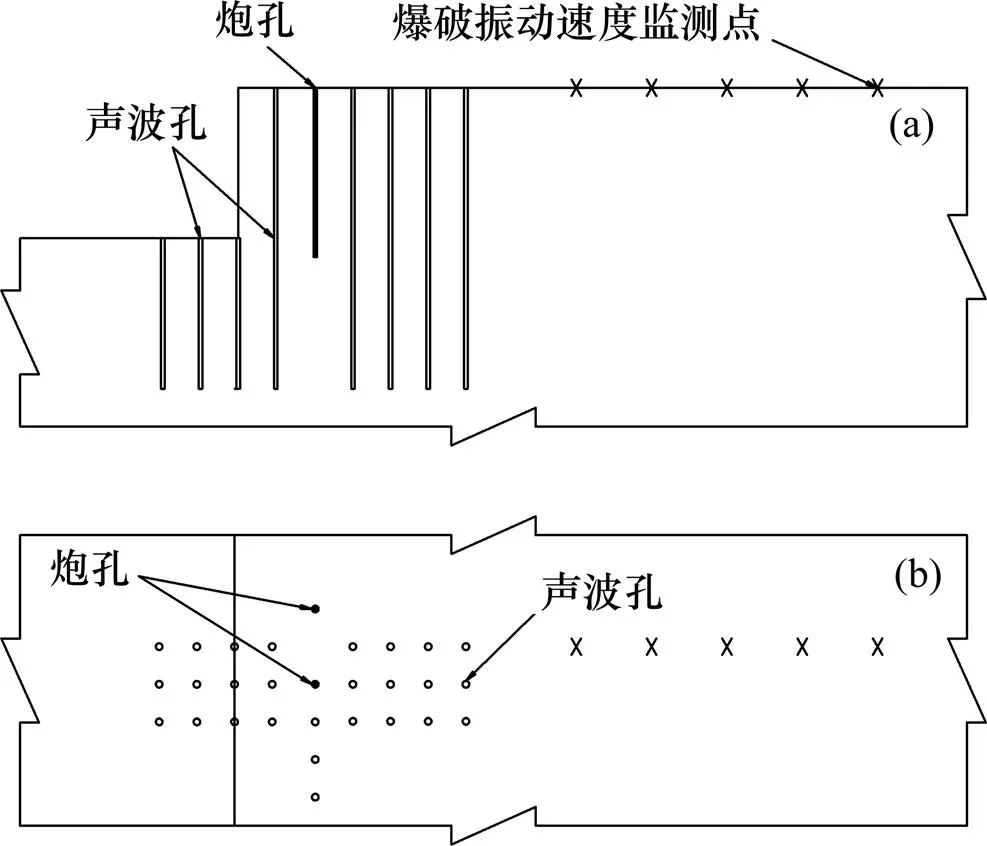
(a) 纵向剖面；(b) 俯视图

3.2 数值建模

3.2.1 几何模型及本构关系

利用有限差分数值软件FLAC3D建立三维爆破数值模型。数值模型的几何示意图见图4。图4中，数值模型长为70.0 m，宽为20.0 m，最大高度为24.0 m，台阶高4.0 m。建立2个垂直向的炮孔单元，炮孔单元的孔距为2.0 m，与台阶的垂直临空面的距离为1.8 m，孔深为4.5 m。加载本构关系采用式(13)~(14)和式(19)~(20)的本构关系式。弹性卸载时，累积的损伤变量不变。体积模量和剪切模量由式(5)~(6)计算。通过编程将提出的本构关系应用到FLAC3D软件中。

3.2.2 边界条件

先进行静力计算，最后进行动力计算，在人工截断竖向边界上采用静应力边界模式。纵向和横向边界静应力根据现场实测取值分别为13 MPa和9 MPa，在人工截断的底部边界上固定位移。动力计算时，在所有人工截断边界上采用无反射黏滞边界模式。在2个炮孔内边界上施加式(17)确定的爆炸荷载。由于轴向不耦合系数和径向不耦合系数均相同，根据式(17)，对于不同装量的炮孔，图2所示的内边界上单位面积爆炸压力不变，变化的是堵塞长度c。根据式(16)，堵塞长度c减小，则单孔药量增加。由式(15)~(16)计算得到爆炸压力时程曲线的峰值压力max=4.0×1010Pa，时程曲线见图5。图5中，爆炸压力的升压时间约为24 μs，压力总作用时间约为300 μs，曲线参数与文献[8]中的计算结果相近。

数据单位：m

图5 炮孔内爆炸压力时程曲线

3.3 试验结果及分析

3.3.1 爆破破坏影响范围特性

定义破坏区边缘至2个炮孔中心连线中点的水平距离为破坏半径c，至炮孔顶部自由面的垂直距离为破坏深度c。爆破破坏影响范围的空间形态由c和c这2个参数决定。由式(19)~(20)得到数值试验爆破破坏判据lim。根据lim判定爆破破坏影响范围。当岩石初始损伤0=0.3，单孔炸药量e=9.0 kg时数值模拟和现场试验得到的纵剖面上爆破破坏影响范围见图6。其中，曲线3和曲线4分别为数值模拟和现场试验得到的爆破影响范围边缘线。该边缘线以上区域为爆破破坏影响范围。从图6可看出：相对垂直方向，爆破破坏影响范围主要向水平方向延伸，这是由爆炸应力波波阵面特性决定的。数值模拟的爆炸应力波近似为径向压缩柱面波，其切向主要为拉应力，故岩石破裂的主要扩展方向为水平向。当爆炸压缩应力波在炮孔顶部自由面反射为径向拉伸波时，岩石进一步发生破裂。随着深度增加，径向拉伸波强度逐渐减小，它的爆破破坏水平半径也不断减小。因此，爆破破坏最大水平半径在炮孔顶部自由面达到最大。此时c=lim(lim为爆破破坏最大水平半径)。数值模拟和现场试验得到的lim分别为2.7 m和3.0 m。总体看，爆破破坏影响范围主要向水平向和自由面(台阶面和炮孔顶部平面)延伸。

1—炮孔；2—截取的台阶破模型轮廓线；3—数值模拟爆破损伤等值线Dlim=0.5；4—现场试验爆破损伤等值线Dlim=0.5。

3.3.2 爆破安全控制

由于工程中要求爆破破坏影响范围不超越保护层，因此，爆破安全控制的关键在于炮孔顶部自由面内破坏半径。p为14，16，18，20 kg时lim与0的关系如图7所示。从图7可看出：爆破破坏最大水平半径随单段爆破药量和岩石初始损伤的增大而增大。

Qmax/kg：1—14.0；2—16.0；3—18.0；4—20.0。

由式(22)得到爆破破坏最大水平半径lim与单段爆破药量p以及岩石初始损伤0的拟合关系为

表达式的拟合相关系数为0.92，数据相关性良好。

当单段爆破药量p=18.0 kg时，岩石初始损伤、破坏半径等参数的关系为

式中：0.25≤0≤0.65。

根据式(25)，当岩石初始损伤从0.25增加至0.30时，爆破破坏最大水平半径增大约5%；当初始损伤从0.50增加至0.55时，爆破破坏最大水平半径增大约8%。可见：随着岩石初始损伤增大，爆破破坏范围沿水平向的扩展速率不断增大。此外，由式(25)可知，当岩石初始损伤0­≥0.6时，lim­≥4.0 m，超过保护层设计最小厚度。因此，岩石初始损伤是爆破参数设计及安全控制需考虑的重要因素。本构模型考虑岩石初始损伤是合理的。临界峰值振动速度与岩石初始损伤之间的关系见图8。从图8可看出：随着0增大，lim减小，两者之间的拟合关系为

式中：0.25≤0≤0.65。

图8 临界峰值振动速度与岩石初始损伤的关系

Fig. 8 Relationship between critical variation velocity and initial damage of rock

式(26)拟合相关系数为0.94，临界峰值振动速度可作为爆破破坏影响判据。当炮孔顶部自由面上的破坏半径小于保护层厚度时，保护层能确保需保护的构(建)筑物安全稳定。考虑到爆破动力破坏和场地因素的复杂性，确定安全允许的爆破炸药量需考虑安全系数，满足下式：

(28)

式中：R和H分别为与单段爆破区域几何中心的水平距离大于或等于保护层厚度最小设计厚度时的水平向和垂直向峰值振动速度。当保护层厚度=4.0 m时，由式(24)和(27)得到安全允许药量和初始损伤的关系为

3.3.3 数值计算结果和现场试验结果对比

试验结果对比的条件：岩石初始损伤为0.3，单孔炸药量为9.0 kg。数值模拟试验和现场试验测定的爆破破坏影响范围对比结果见图6，爆破破坏影响范围参数对比见表1。从图6可看出两者测定的爆破破坏影响范围差别不大。从表1可看出：数值模拟试验测定的爆破破坏最大水平半径为2.7 m，现场试验测定的爆破破坏最大水平半径为3.0 m，均小于保护层的厚度4.0 m，数值计算得到的爆破破坏最大水平半径相对现场试验减小约10%，数值模拟试验测定的临界峰值振动速度相对现场试验结果的相对误差约为8%。

沿炮孔顶部平面相同传播路径提取质点峰值振动速度，峰值振动速度随距离衰减的对比见表2。表2中，为测点至爆炸中心的水平距离。当2.7≤≤40.0且相同时，数值计算结果与现场结果的相对误差不超过13%。峰值振动随距离的增大而衰减。现场试验和数值模拟得到的峰值振动速度衰减系数对比：对于水平径向，分别为1.35和1.28，相对误差约为5%；对于垂直向，则分别为1.44和1.38，相对误差约为4%。

表1 爆破破坏影响范围试验结果对比

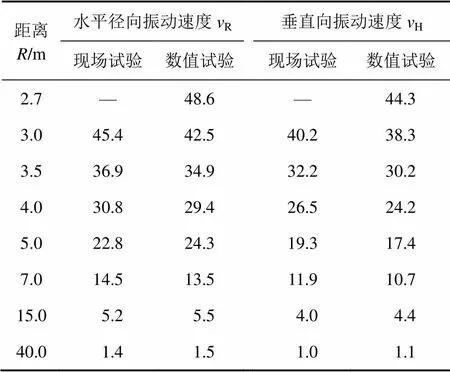
表2 峰值振动速度衰减对比

对比数值试验结果和现场试验结果，测定的爆炸近区破坏影响范围和中远区爆破振动衰减规律都较接近。虽然两者得到的结果间存在一定差别(经初步分析，这种差异主要由场地因素的复杂性引起)，但相对误差不超过13%，因此，本文提出的爆破损伤理论模型及数值模型较合理。此外，现场爆破试验测定的爆破破坏影响范围未超过保护层厚度设计值，因此，实际施工可在现场试验的基础上调整爆破参数。

4 结论

1) 爆破破坏影响范围主要向水平方向扩展。地表自由面反射拉伸的爆炸应力波使浅孔台阶水平向爆破破坏影响范围随深度的增加而减小，破坏范围沿水平向的扩展在炮孔顶部平面达到最大值。与炮孔顶部平面的破坏区边缘对应的质点峰值振动速度和岩石初始损伤或者岩体完整程度相关，可应用于施工期安全监测对爆破破坏影响范围的判定。

2) 大孔径浅孔台阶开挖爆破参数设计和保护层厚度设计都是合理的，爆破破坏影响范围扩展没有超过保护层，爆破区域周边重要构筑物的安全稳定性得到保障。此外，当单段爆破药量一定时，随岩石初始损伤增加，爆破破坏最大水平半径的增大显著。因此，考虑岩石初始损伤的理论模型是合理的。

3)数值计算结果和现场试验结果较一致，数值计算模型较合理。由于爆破损伤数值模型和爆破安全判据等均考虑了岩石初始损伤与岩体完整性指数、声波波速等常用参数的关系，因此，通过初始损伤和岩体完整性指数的关系，可在爆破安全评价中进一步分析岩体完整程度的影响。总体看，研究成果能解决工程实际问题且方便工程应用。因场地条件的复杂性，理论模型和数值计算模型均进行了一定程度的简化，因此，研究成果存在一定局限性，但对类似的大型地下洞室的开挖爆破安全控制仍具有一定的参考价值。

参考文献：

[1] AHRENS T J, RUBIN A M. Impact-induced tensional failure in rock[J]. Geophys Res, 1993(98): 1185−1203.

[2] 朱传云, 喻胜春. 爆破引起岩体损伤的判别方法研究[J]. 工程爆破, 2001, 7(1): 12−16. ZHU Chuangyun, YU Shengchun. Study on the criterion of rockmass damage caused by blasting[J]. Engineering Blasting, 2001, 7(1): 12−16.

[3] 严鹏, 卢文波, 单治钢, 等. 深埋隧洞爆破开挖损伤区检测及特性研究[J]. 岩石力学与工程学报, 2009, 28(8): 1552−1561. YAN Peng, LU Wenbo, SHAN Zhigang, et al. Detecting and study of blasting excavation-induced damage of deep tunnel and its characters[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1552−1561.

[4] 杨卫风, 白伟亮, 翟传明. 爆破震动对小净距隧道岩体损伤的声波测试[J]. 质量检测, 2014, 32(9): 27−30. YANG Weifeng, BAI Weiliang, ZHAI Chuanming. The sound wave test of blasting vibration for tunnel rock mass damage[J]. Quality Test, 2014, 32(9): 27−30.

[5] 卢文波, 李海波, 陈明, 等. 水电工程爆破振动安全判据及应用中的几个关键问题[J]. 岩石力学与工程学报, 2009, 28(8): 1513−1520.

LU Wenbo, LI Haibo, CHEN Ming, et al. Safety criterion of blasting vibration in hydropower engineering and several key problems in their application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1513−1520.

[6] 张文煊, 卢文波. 龙滩水电站地下厂房开挖爆破损伤范围评价[J]. 工程爆破, 2008, 14(2): 1−7. ZHANG Wenxuan, LU Wenbo. Evaluation of blast-induced damage zone in excavation blasting of Longtan underground workshop[J]. Engineering Blasting, 2008, 14(2): 1−7.

[7] 张国华, 陈礼彪, 夏祥, 等. 大断面隧道爆破开挖围岩损伤范围试验研究及数值计算[J]. 岩石力学与工程学报, 2009, 28(8): 1611−1619. ZHANG Guohua, CHEN Libiao, XIA Xiang, et al. Numerical simulation and experimental study of damage range of surrounding rock in large tunnel under blasting excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1611−1619.

[8] 夏祥. 爆炸荷载作用下岩体损伤特征及安全阈值研究[D]. 武汉: 中国科学院研究生院, 2006: 41−62. XIA Xiang. Study on damage characteristics and safety threshold of rock vibration by blast[D]. Wuhan: Chinese Academy of Sciences. Institute of Rock and Soil Mechanics, 2006: 41−62.

[9] 李新平, 陈俊桦, 李友华, 等. 溪洛渡电站地下厂房爆破损伤范围及判据研究[J]. 岩石力学与工程学报, 2010, 29(10): 2042−2048. LI Xinping, CHEN Junhua, LI Youhua, et al. Study of criterion and damage zone induced by excavation blasting of underground power-house of Xiluodu hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2042−2048.

[10] 曹文贵, 赵衡, 张玲, 等. 考虑损伤阀值影响的岩石损伤统计软化本构模型及其参数确定方法[J]. 岩石力学与工程学报, 2008, 27(6): 1149−1154. CAO Wengui, ZHAO Heng, ZHANG Ling, et al. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1149−1154.

[11] YANG R, BRWDEN W F, KATSABANIS P D. A new constitutive model for blast damage[J]. International Journal of Rock Mechanics and Mining Sciences, 1996, 33: 245−254.

[12] 陈俊桦, 张家生, 李新平. 考虑岩体完整程度的岩石爆破损伤模型及应用[J]. 岩土工程学报, 2016, 38(5): 855−866. CHEN Junhua, ZHANG Jiasheng, LI Xinping. Model of rock blasting-induced damage and its application based on the integrity of rockmass[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 855−866.

[13] 刘新东, 郝际平. 连续介质损伤力学[M]. 北京: 国防工业出版社, 2011: 241−253. LIU Xindong, HAO Jiping. Damage mechanics of continuous media[M]. Beijing: National Defense Industry Press, 2011: 241−253.

[14] 王小委, 陈洪凯, 廖云平. 爆破冲击作用下岩体损伤范围研究[J]. 工程地质学报, 2014, 22(2): 233−237. WANG Xiaowei, CHEN Hongkai, LIAO Yunping. Damage zone of sandstone under blasting impact[J]. Journal of Engineering Geology, 2014, 22(2): 233−237.

[15] 杨建华, 卢文波, 胡英国, 等. 隧洞开挖重复爆炸荷载作用下围岩累积损伤特性[J]. 岩土力学, 2014, 35(2): 511−518. YANG Jianhua, LU Wenbo, HU Yingguo, et al. Accumulated damage in surrounding rocks due to repeated blasting loads during blasting excavation of tunnels[J]. Rock and Soil Mechanics, 2014, 35(2): 511−518.

[16] 钟明寿, 龙源, 谢全民, 等. 炮孔不同耦合介质对碳酸盐岩爆炸地震信号影响分析[J]. 岩石力学与工程学报, 2011, 30(4): 702−708. ZHONG Mingshou, LONG Yuan, XIE Quanmin, et al. Effect analysis of different borehole coupling media on explosion seismic signal of carbonate rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 702−708.

[17] 李宁. 爆破荷载的数值模拟与应用[J]. 岩石力学与工程学报, 1994, 13(4): 357−364. LI Ning. A numerical model for blast load and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 1994, 13(4): 357−364.

(编辑 陈灿华)

Rock blasting-induced damage zone under blasting excavation in a large underground chamber

CHEN Junhua1, ZHANG Jiasheng1, LI Xinping2

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Hubei Key Laboratory of Road-Bridge and Structure Engineering, Wuhan University of Technology, Wuhan 430070, China)

The rock mass integrity was usually considered to have great influence on blasting excavation in a large underground chamber. Taking the short-hole blasting as research background for bench excavation of the main underground workshop with super-large section in Xiluodu hydroelectric power plant, located in the Jinsha River，at the junction of Sichuan and Yunnan in China, a model of rock blasting-induced damage taking initial damage into account was presented based on damage mechanics. The criterion for blasting-induced damage, which was related to the initial damage of rock, was also presented for determining the blasting-induced damage zone. The formula about the relation between the initial damage of rock and the integrity index of rock mass was proposed so that the presented model could consider the integrity of rock mass. The presented model was imported into the software FLAC3D by programming the numerical simulation for rock mass integrityion of blasting. Firstly, The analysis of the characteristics of rock blasting-induced damage zone of surrounding rock were made. Secondly, the maximum radius of blasting-induced damage zone in the horizontal-radial direction was considered as the characteristic parameter for the blasting-induced damage zone. The relations among the maximum horizontal radius of blasting-induced damage zone, the initial damage of rock, the blasting charge amount per delay interval and the peak particle velocity of vibration were also analyzed. As a result, the limited velocity of vibration and the safety charge amount corresponding to the rock damage under different initial damage were obtained. In the end, the results from tests on site including blasting tests, testing of peak particle vibration velocity and velocity of acoustic wave propagation in a borehole, were put forward. The rationality of numerical simulation was verified by the result comparisons between the tests on site and the numerical simulation. The results show that, for the short-hole bench blasting, the blasting-induced damage zone decreases with increment of blasthole depth in the horizontal-radial direction, and it expands to the maximum on the top free face of blasthole. The peak vibration velocity of particle located in the edge of blasting-induced damage on the top free face of blasthole can be used as the safety criterion for evaluating rock blasting-induced damage in the excavation monitoring process. The initial damage value of rock has remarkable influence on the maximum blasting-induced damage radius when the value is big. The results obtained from numerical simulation are in good agreement with those from tests on site.

rock mechanics; underground workshop of hydroelectric power plant; criterion for blasting safety; numerical simulation of blasting; peak particle vibration velocity; integity of rock mass

10.11817/j.issn.1672-7207.2016.11.026

TD235；TV542

A

1672−7207(2016)11−3808−10

2015−11−12；

2016−01−15

国家自然科学基金资助项目(51274157，51378514) (Projects(51274157, 51378514) supported by the National Natural Science Foundation of China)

陈俊桦，博士研究生，从事岩土工程、爆破工程的研究；E-mail: jhchan@126.com