一种摆式球形水下机器人水底滚动特性分析

李艳生，孙汉旭，贾庆轩，张延恒，褚明



一种摆式球形水下机器人水底滚动特性分析

李艳生1, 2，孙汉旭1，贾庆轩1，张延恒1，褚明1

(1. 北京邮电大学自动化学院，北京，100876；2. 重庆邮电大学先进制造工程学院，重庆，400065)

为了更加深入的掌握BYSQ-2球形水下机器人水底滚动特性，在建立机器人水底滚动方程基础之上，分析得出机器人质量和电机转速也会对机器人的水底滚动产生影响。搭建该种水下机器人水底仿真环境平台和虚拟样机，通过对比在不同质量和电机转速下的仿真结果，得出该种球形水下机器人水底滚动的波动特点，并且增加机器人的质量和降低电机的转速，会有效的提高机器人在水底滚动的稳定性。

球形机器人；无人水下航行器；水底滚动；虚拟仿真

无人水下机器人(autonomous underwater vehicles, AUV)已经在民用领域、工业领域和科学研究领域中广泛应用，近年来又在军用领域得到重视。美国海军针对无人水下航行器的优势，制定了9类使命任务，并且充分肯定了以潜艇携带水下航行器的优点[1−2]。球形机器人成功着落在水底，可以利用自身装载的传感器就可以近距离的对水底生物环境进行考察，拍摄水底地貌和获取水文信息等[3−4]。球形机器人在水底有时需要偏离原来的着陆位置，进行短距离移动。通过启动螺旋桨使机器人上浮，然后控制运动到预定地点进行着底运动的方式对于短距离的移动过于繁琐。本文研究的运动灵活的球形水下机器人BYSQ-2，在水底探测方面具有很大的优势，能够以滚动的方式进行姿态调整和位置变换。本文设计方案中的球形机器人通过重摆的重力矩来驱动球形机器人进行姿态调整和向前滚动。段海庆等[5−6]对水下机器人进行水底探测时的欠驱动控制与水底地形跟踪控制进行了深入研究。郑一力等[7−8]对球形机器人在陆地滚动的特性进行了分析，尤其是球形机器人重摆的稳定性。为了更加深入的掌握该种球形水下机器人在硬质平坦水底姿态变换和水底滚动情况，本文作者首先建立了球形机器人在水底的滚动数学模型，导出球形机器人的质量参数和重摆电机的转动速度对机器人在水底滚动有重要影响。然后在建立机器人水底滚动的Adams虚拟样机仿真模型的基础上，对球形机器人在水底滚动的特性和影响因素进行了充分的仿真分析和总结。

1 机器人实物样机

BYSQ-2水下机器人与陆地球形机器人[6]有很大相似之处，机器人长轴与推进螺旋桨轴心共线，长轴电机可以用来调整横滚角度。机器人短轴轴线与长轴轴线垂直，短轴电机用来调整机器人俯仰角度。机器人内部控制电路和驱动电机全部密封在一个圆形玻璃纤维球壳内，其物理样机实物如图1所示。

图1 机器人的样机和模型

表1 物理参数

2 水底滚动数学模型

在水底环境下，球形机器人的滚动速度受到的水阻力不可忽略，并且由于水的浮力影响，机器人的对水底的压力会减小，从而降低球壳与水底的摩擦 力[9−10]。对球形水下机器人进行水底运动分析，首先要建立动力学模型来确定研究参数，本方案中的球形水下机器人系统在水底滚动时，以球壳为研究对象的受力示意图如图2所示。

图2 球壳受力示意图

图2所示半径为的球形机器人在水底向前以角速度向前滚动时的受力情况，在球壳与水底接触点处，水底对球壳有摩擦力和支持力的作用，同时也受到周围流体对球壳的水阻力D和浮力的作用。机器人系统内部重摆机构也会对机器人施加水平分力F，竖直分力F和转动力矩，同时机器人自身的球壳部分结构也受到重力作用。根据力学平衡和牛顿欧拉定理，可以得到球形机器人在水底滚动的球壳力学方程：

同理，对整个球形机器人系统水底运动受力分析，除了球壳部分外，还要对内部重摆驱动机构进行受力分析[11−12]，以重摆为研究对象的受力分析如图3所示。

图3 重摆受力示意图

Fig. 3 Force diagrams of heavy pendulums

式(1)和(2)中的水平分力F和，竖直分力F和，转动力矩和为成对出现的作用力与反作用力，根据牛顿第三定律可以得到这3对力和力矩分别对应大小相等。将重摆机构的力学方程带入球壳力学程，消去相互作用力可得如下方程组：

(3)

球形机器人在水底滚动状态时的质量与悬浮状态时的配平质量差Δ和摩擦力又可表示为

球形机器人在水底滚动时，其驱动力矩是通过重摆电机驱动重摆的摆动，反作用力矩驱动球壳滚动，实质上可以看作机器人的滚动运动函数是电机转动的函数。电机转动角度与重摆摆角和机器人滚动速度之间建立的约束关系为

(5)

将式(5)代入方程(3)得球形机器人水底滚动力学方程：

从上面的方程可以看出球形水下机器人在水底滚动和姿态调整，不但与重摆驱动电机的转动角度变化过程有关，而且还和球形机器人的配平质量Δ有关。显然，对球形机器人水底运动规律和相关参数影响规律的总结是必要的。

3 机器人仿真模型

为了清晰地分析这2个参数对球形机器人在水底运动的影响，通过建立Adams样机模型，添加水底约束条件，在变参数条件下仿真运动情况。在建立水底滚动动力学模型时，将机器人分为2个部分：一部分质量等效集中在球壳中心处，另一部分质量等效集中在重摆质心处[13−14]。建立球形机器人水底滚动虚拟样机，球形机器人系统主要被简化为配重部分和球壳部分，其中能够与重摆机构一起摆动的部件，其质量全部被等效集中到重摆质心，而和球壳固定在一起，能和球壳一起转动的部件，其质量全部被等效集中在球壳中心。球形机器人水底滚动分析涉及水动力学和刚体动力学，Adams软件可以仿真来球形机器人内部的重摆摆动与球壳滚动的规律。但是对于水动力部分，需要将Fluent水动力系数结果加入，作为仿真约束条件。球形机器人在水中的旋转阻力，在水底滚动的滚动摩阻系数很小，系统各个零件间的摩擦力的能量损耗也很小，仿真时忽略这些因素影响。根据上述原则，三维模型并导入Adams虚拟环境中[15−16]。

(a) 球壳与水底模型；(b) 内部重摆模型

在虚拟仿真中，水底被建立成一个比球形机器人大很多的薄平板，被设置成刚体与大地固连。等效球壳与等效重摆也被设置成刚体，重摆与球壳之间设置成转动副。球壳和水底两刚体之间设置为接触副。设定水的密度为1 000 kg/m3，重力加速度为10 m/s2，由于球形机器人的具有完美对称性，可将浮力、重力和水动力施加在球壳中心，根据样机模型，球壳直径为500 mm，浮力为654 N，其中水动力与球形机器人本身在水底运动的速度和加速度等运动参数有关，根据Fluent软件水动力仿真数据，设定与速度二次方项有关的阻力系数被设置为40.2，与加速度有关附加质量系数被设置为32.7。因此在Adams中机器人的球心处添加水动力约束条件。

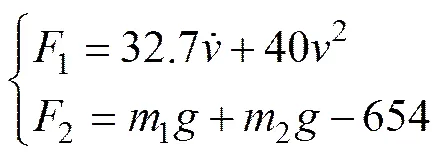
其中：水平方向力1的方向与机器人运动方向相反，竖直方向力2的方向与重力方向相同。

4 水底滚动仿真结果

基于上面建立的球形机器人样机和水底运动环境条件设定，在Adams环境中分别对带有水动力和浮力条件下的水底滚动进行仿真分析，机器人质量为60 kg，重摆驱动电机转速为π rad/s，启动10 s内的仿真结果如图5所示。由图5可以看出：球形机器人在水底滚动，速度(图5(a))、摆角(图5(b))和电机力矩(图5(c))都是波动的，波动幅值逐渐衰减，输出力矩基本位于轴上方，表示要机器人向前滚动要持续输出 力矩。

在得到机器人在水底滚动的仿真结果后，进一步研究机器人水底滚动特性。在原来样机模型基础上，球壳质量变化Δ为10 kg的条件下进行仿真，分析研究配平质量因素对滚动特性的影响。

由图5和图6可以看出：球形机器人在水底滚动过程中，其运动特性受机器人配平质量影响较大。从位移曲线中可以看出在相同时间内配平质量增加，球形机器人在水底滚动距离变大；从摆角曲线中可以看出配平质量增大，球形机器人重摆摆动幅值衰减较快；从力矩曲线中可以看出配平质量增大，球形机器人在水底滚动力矩波动的幅值变小。从仿真结果可以得出配平质量增加，可以增强球形机器人水底滚动的稳定性。

在重摆电机驱动转速为1.5πrad/s，其他参数不变的条件下进行仿真，分析研究电机转动速度对滚动特性的影响。

由图5和图7可以看出：球形机器人在水底滚动过程中，其运动特性受机器人重摆电机转动速度影响较大。从位移曲线中可以看出在相同时间内球形机器人滚动的距离并不与转动速度成正比；从摆角曲线中可以看出电机转速增大，球形机器人重摆摆动幅值衰减较慢，波动频率变大；从力矩曲线中可以看出电机转动速度增大，球形机器人在水底滚动力矩波动的幅值增加。从仿真结果可以得出仅仅增加电机驱动转速对提高机器人水底移动速度不明显，并且稳定性受到破坏。

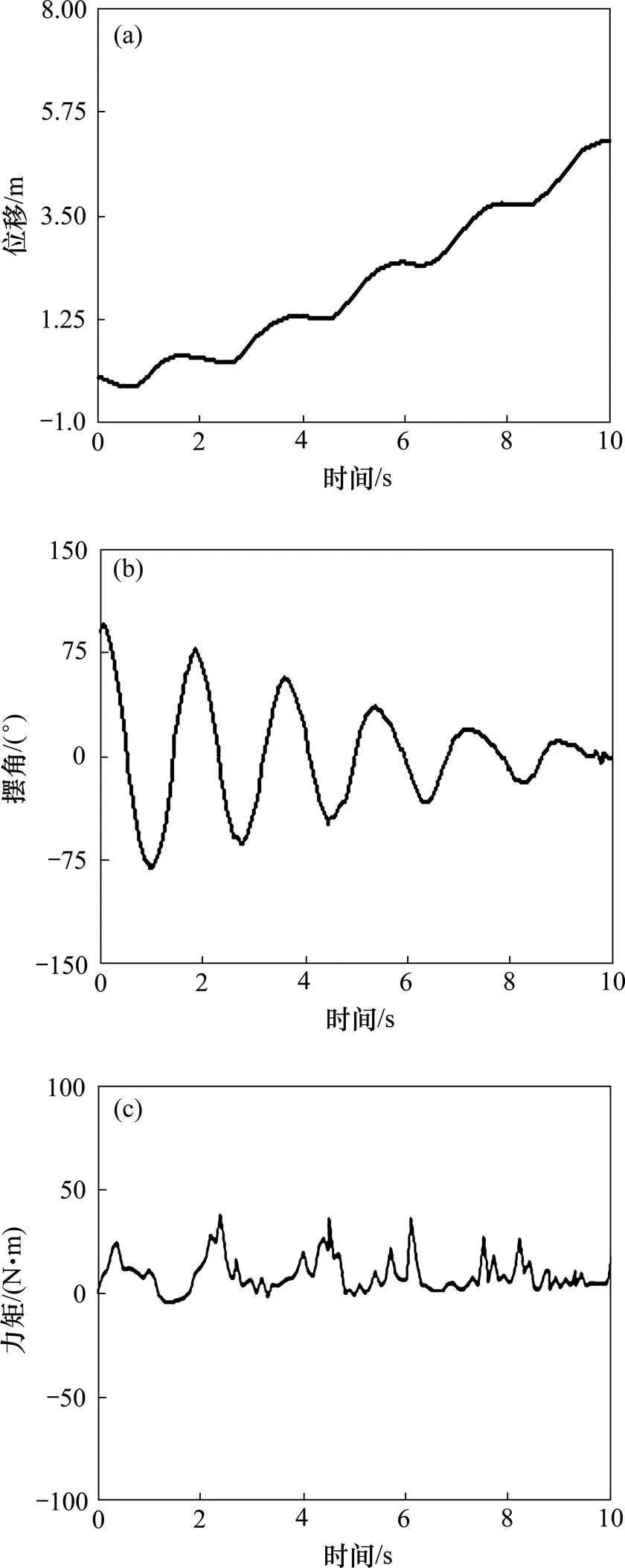
(a) 位移；(b) 摆角；(c) 力矩

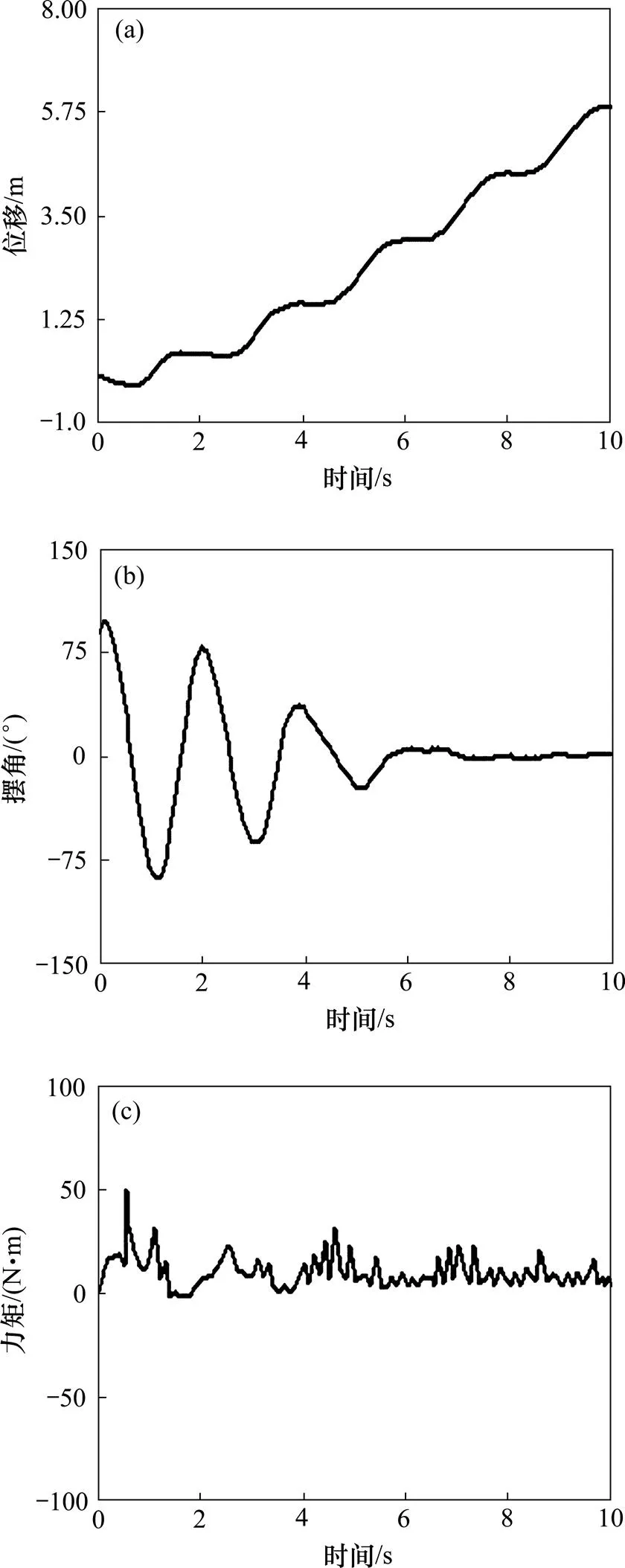
(a) 位移；(b) 摆角；(c) 力矩

(a) 位移；(b) 摆角；(c) 力矩

5 结论

1) 摆式球形水下机器人在水底滚动时，重摆电机以恒角速度输出时，机器人的位移是波动曲线，表明滚动速度是周期性变化的，并且机器人的重摆摆动角度和电机的输出力矩也是表现周期性波动变化。

2) 通过建立球形机器人水底滚动数学模型发现，滚动特性受机器人质量和电机转速影响。仿真结果表明，机器人质量增大会提高滚动的稳定性，而增加电机转速会破坏这种稳定性。

参考文献：

[1] 陈强, 张林根. 美军军用UUV现状及发展趋势分析[J]. 舰船科学技术, 2010, 32(7): 129−134. CHEN Qiang, ZHANG Lingen. Analysis of current situational development trend of US military UUV[J].Ship Science and Technology, 2010, 32(7): 129−134.

[2] 姜军, 宋保维, 潘光, 等. 超低速小型AUV外形及流体动力布局研究[J]. 鱼类技术, 2011, 19(5): 321−324. JIANG Jun, SONG Baowei, PAN Guang, et al. Study on design of shape and hydrodynamic layout for ultra-low-speed AUV[J]. Torpedo Technology, 2011, 19(5): 321−324.

[3] WATSON S A, GREEN P N. A de-coupled vertical controller for micro-autonomous underwater vehicles (μAUVs)[C]// Mechatronics and Automation (ICMA). Washington DC, USA: IEEE Computer Society, 2010: 561−566.

[4] GUO S, LIN X, TANAKA K, et al. Modeling of water-jet propeller for underwater vehicles[C]// Proceedings of the 2010 IEEE International Conference on Automation and Logistics. Washington DC,USA: IEEE Computer Society, 2010: 92−97.

[5] 段海庆,贾鹤鸣, 周佳如. 基于神经网络的欠驱动水下机器人地形跟踪控制[J]. 东南大学学报(自然科学版), 2012, 42(Sup1): 203−207. DUAN Haiqing, JIA Heming, ZHOU Jiaru. Bottom following control for underactuated AUV based on neural network[J]. Journal of Southeast University (Natural Science Edition), 2012, 42(Sup1): 203−207.

[6] 张立军, 齐雪, 赵杰梅.垂直面欠驱动自治水下机器人定深问题的自适应输出反馈控制[J]. 控制理论与应用, 2012, 29(10): 1371−1376. ZHANG Lijun, QI Xue, ZHAO Jiemei. Depth-keeping control for autonomous underwater vehicle in vertical plane using adaptive output feedback controller[J]. Control Theory & Applications, 2012, 29(10): 1371−1376.

[7] 郑一力, 孙汉旭. 带高速旋转飞轮的球形机器人结构设计与运动稳定性分析[J]. 机械工程学报, 2013, 49(3): 36−41. ZHENG Yili, SUN Hanxu. Mechanical design and motion stability analysis of a spherical robot equipped with high-rate flywheel[J]. Journal of Mechanical Engineer, 2013, 49(3): 36−41.

[8] 于涛, 孙汉旭, 贾庆轩. 一类欠驱动的解耦滑模控制方法[J]. 东南大学学报(自然科学版), 2012, 42(Sup1): 11−14. YU Tao, SUN Hanxu, JIA Qingxuan. Decoupled sliding mode control for a class of underactuated systems[J]. Journal of Southeast University (Natural Science Edition), 2012, 42(Sup1): 11−14.

[9] 兰晓娟, 孙汉旭, 贾庆轩. 水下球形机器人BYSQ_2的原理与动力学分析[J]. 北京邮电大学学报, 2010, 33(3): 20−23. LAN Xiaojuan, SUN Hanxu, JIA Qingxuan. Principle and dynamic analysis of a new-type spherical underwater vehicle[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(3): 20−23.

[10] LAN Xiaojuan, SUN Hanxu, JIA Qingxuan. The hydrodynamic analysis for the underwater robot with a spherical hull[C]// Proceedings of SPIE-The International Society for Optical Engineering, Space Exploration Technologies II.Bellingham USA:SPIE, 2009: 73310E-1−73310E-8.

[11] 俞建成, 张奇峰, 吴利红, 等. 水下滑翔机器人运动调节机构设计与运动性能分析[J]. 机器人, 2005, 27(5): 390−395. YU Jiancheng, ZHANG Qifeng, WU Lihong, et al. Movement mechanism design and motion performance analysis of an underwater glider[J]. Robot, 2005, 27(5): 390−395.

[12] 高丙团, 陈宏钧, 张晓华. 龙门吊车系统的动力学建模[J]. 计算机仿真, 2006, 23(2): 50−109. GAO Bingtuan, CHEN Hongjun, ZHANG Xiaohua. Dynamic modeling of a gantry crane system[J]. Computer Simulation, 2006, 23(2): 50−109.

[13] 王鹏飞, 王鑫, 李满天, 等. 一款微小型球形机器人的动力学分析[J]. 哈尔滨工业大学, 2010, 42(9): 1398−1402. WANG Pengfei, WANG Xin, LI Mantian, et al. Dynamics analysis of a micro-spherical robot[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1398−1402.

[14] 占强, 贾川, 马晓辉, 等. 一种球形机器人运动性能分析[J]. 北京航空航天大学, 2005, 31(7): 744−747. ZHAN Qiang, JIA Chuan, MA Xiaohui, et al. Analysis of moving capability of a spherical mobile robot[J]. Journal o f Beijing University of Aeronautics and Astronautics, 2005, 31(7): 744−747.

[15] 刘贵杰, 王猛, 何波, 等. 基于Adams与Matlab/Simulink的水下自航行器协同仿真[J]. 机械工程学报, 2009, 45(10): 22−29. LIU Guijie, WANG Meng, HE Bo, et al. Cooperative simulation based on Adams and Matlab/Simulink for autonomous underwater vehicle[J]. Journal of Mechanical Engineer, 2009, 45(10): 22−29.

[16] 马鑫, 丑武胜, 方斌, 等. 基于Pro/E和ADAMS的水下机器人设计方法研究[J]. 机械工程与自动化, 2013, 45(6): 3−5. MA Xin, COU Wusheng, FANG Bin, et al. ROV design method based on Pro/E and ADAMS[J]. Mechanical Engineering & Automation, 2013, 45(6): 3−5.

(编辑 陈爱华)

Analysis of rolling characteristics at water bottom for spherical robot with heavy pendulums

LI Yansheng1, 2, SUN Hanxu1, JIA Qingxuan1, ZHANG Yanheng1, CHU Ming1

(1. Institute of Automation, Beijing University of Posts and Telecommunications, Beijing 100876; 2. School of Advanced manufacturing engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065)

In order to know the robot rolling characteristics of BYSQ-2 spherical underwater, the rolling equation was established and an impact on rolling at the bottom of water was analyzed with the robot’s quality and the motor’s speed. After making comparison of the rolling characteristics under water with different quality and motor speed, the simulation results show the volatility characteristics and show that increasing the quality and the moderate motor speed can effectively improve the rolling stability of the robot at the bottom of water.

spherical robot; unmanned underwater vehicle; neural network control; sliding mode method

10.11817/j.issn.1672-7207.2016.11.007

TP242

A

1672−7207(2016)11−3664−06

2016−01−08；

2016−04−07

国家自然科学基金资助项目(51175048) (Project(51175048) supported by the National Natural Science Foundation of China)

李艳生，博士，从事特种机器人研究；E-mail: liyansheng0@163.com