SiHCl3-H2体系多晶硅化学气相沉积的传递−动力学模型
侯彦青,聂陟枫,谢刚,马文会,戴永年,俞小花,宋东明
SiHCl3-H2体系多晶硅化学气相沉积的传递−动力学模型
侯彦青1, 2,聂陟枫1, 2,谢刚2, 3,马文会1, 2,戴永年2,俞小花2,宋东明2
(1. 昆明理工大学省部共建复杂有色金属资源清洁利用国家重点实验室,云南昆明,650093;2 昆明理工大学冶金与能源工程学院,云南昆明,650093;3. 昆明冶金研究院,云南昆明,650031)
提出SiHCl3-H2体系多晶硅化学气相沉积的传递−动力学模型(TKM),同时考虑传递过程和表面化学反应动力学对硅沉积速率的影响。研究硅沉积过程受表面化学反应速率限制和传递速率限制的边界条件,并且研究表面化学反应速率受氢气浓度限制或SiHCl3(TCS)浓度限制的边界条件,提出同时受氢气浓度限制和TCS 浓度限制的边界条件。为了验证TKM的有效性,应用该模型计算硅棒长度为2 m、硅棒直径为10 cm、气流速度为0.67 m/s、硅棒表面温度为 1 398 K、常压(0.1 MPa)条件下,不同H2/SiHCl3配比下的硅沉积速率。研究结果表明:通过TKM的计算结果与Habuka所测得的实验数据比较,相对误差为3.6%(小于10%),表明该模型准确可靠。
传递−动力学模型;多晶硅;化学气相沉积;硅沉积速率;传递现象
随着全球范围内传统能源的枯竭以及石油价格的不断攀升,太阳能作为环境友好能源受到全世界的广泛关注。尤其是如何生产高效率、低费用的太阳能电池成为科学家的研究重点。多晶硅是作为光伏转换器最好的材料之一,95%的太阳能电池都是以硅作为基材[1]。在未来50多年的时间内,还很难发现其他材料能替代硅成为电子和光伏产业的主要材料[2]。多晶硅的主要生产方法有西门子法、冶金法、硅烷法、锌还原法等[3−4],其中西门子法是目前国际主流厂商生产多晶硅的主要工艺[5]。尽管改良西门子法的工业生产很成熟,但是高能耗和高生产成本是阻碍该方法发展的巨大挑战,并且为了满足日益增长的多晶硅需求,很多生产商都在扩大生产规模。因此需要对西门子反应器内的传递现象进行模拟,从而更加深入的了解该过程。通过改善反应器的设计和操作条件降低能耗和减少生产成本,为扩大化生产提供理论依据。YANG[6]提出了CSTR模型,该模型假设气体在反应器中充分混合。该模型对改进西门子反应器提供了理论依据,然而TCS与氢气反应制备多晶硅的反应速率受温度的影响很大[7]。在低温条件下,硅的沉积速率是由反应速率限制。由于反应速率很低,硅棒表面反应物的浓度基本等于进料浓度。在高温条件下,硅的沉积速率是由反应物的传递过程限制。由于化学反应的速率很大,硅表面的反应物的浓度远小于通入反应器时的进料浓度。于是一系列的传递或(和)化学反应限制模型发展起来,FALLER等[8]在1999年提出了化学反应限制模型,该模型假设硅棒表面的反应物浓度等于通入反应器时的初始浓度,忽略了传递对该过程的影响。HABUKA等[9−13]在1996年提出了硅的外延生长完全模型,并在近几年对该模型进行完善。在此基础上,张攀等[14]也研究了多晶硅化学气相沉积的压力、进料配比、温度、进料流量等对硅沉积速率的影响。然而该模型仅研究了多晶硅薄膜的外延生长,对改良西门子法中多晶硅的生长并没有做深入的探讨,并且仅考虑了多晶硅生产的主反应,忽略HCl对硅的侵蚀反应。国内关于西门子反应器的模拟研究主要专注于温度场和流场的研究,如管俭等[15]通过流场和温度场的耦合研究了还原炉的温度场分布;王子松等[16]研究了西门子还原炉内流场和温度场,并提出降低能量损失的方法;凌猛等[17]通过热辐射传递模拟计算了多晶硅还原炉内热量传递现象。这些研究可以为改进反应器结构以及节能提供一定的依据,然而未涉及质量传递现象,对多晶硅的表面反应及气相反应未做深入的分析,无法得到操作条件及反应器结构对硅沉积速率的影响。因此,以上研究对改良西门子法制备多晶硅的实际生产的指导意义是有限的。为了更好地指导生产,必须发展西门子反应器的完全模型。COSO等[18]提出了西门子反应器的完全模型,然而该模型具有以下缺陷:1) 忽略了气体在反应器中的方向上的动量传递。2) 化学反应只考虑了主要反应且忽略了该反应的逆反应。由于该反应的主要副产物HCl在硅棒表面的浓度受传递过程的限制,因此不可忽略HCl对该过程化学反应的影响,即不能忽略该过程的逆反应。3) 该过程在氢气浓度较低时,化学反应速率受氢气浓度限值;当氢气浓度很高时,化学反应速率受SiHCl3(TCS)浓度限值。但是当氢气的浓度在中等浓度时,化学反应同时受氢气和TCS浓度的共同限值。实际上,生产过程中所采用的氢气浓度是处于中等水平,但是该模型只考虑了氢气浓度限值或TCS浓度限值。张攀等[19]应用Fluent软件研究了各因素对12对棒还原炉的硅沉积速率的影响,CAVALLOTTI等[20]也研究各因素6对棒还原率的硅沉积速率。然而这两个研究更偏向于应用软件对该过程进行模拟,对该过程的表面反应动力学以及传递现象并未进行深入的研究,且Coso模型中遇到的问题[18],这两个模型依然没有解决。由于已存在的模型都存在一定的缺陷,因此,本文作者提出了多晶硅化学气相沉积的传递−动力学模型,即化学反应限制和传递过程限制模型,并且当过程受化学反应限制时,考虑了化学反应的逆反应。分析了化学反应受氢气浓度限制和TCS浓度限制的条件,并发展了该过程受氢气浓度限制、TCS浓度限制和受两者共同限制模型。传递−动力学模型加入了方向上的动量传递和热扩散现象,考虑了副反应对硅沉积速率的影响,并且同时研究TCS浓度或(和)H2浓度限值条件,可以更真实的反应改良西门子法多晶硅沉积过程。
1 模型假设
在西门子反应器内部,每对硅棒都是对称的。因此在每对相邻的硅棒之间都有一个封闭的隔绝层,即在隔绝层没有热量和质量传递。反应器内部的硅棒数量以及排列方式的不同,隔绝层的形状也不相同,比如:六边形、圆形、圆柱形、椭圆形等。为了研究问题的方便,本文选用圆柱形隔绝层。可设定一个内空的几何结构,如图1所示。其中i为硅棒的直径,0为隔绝层的直径,为硅棒的长度。
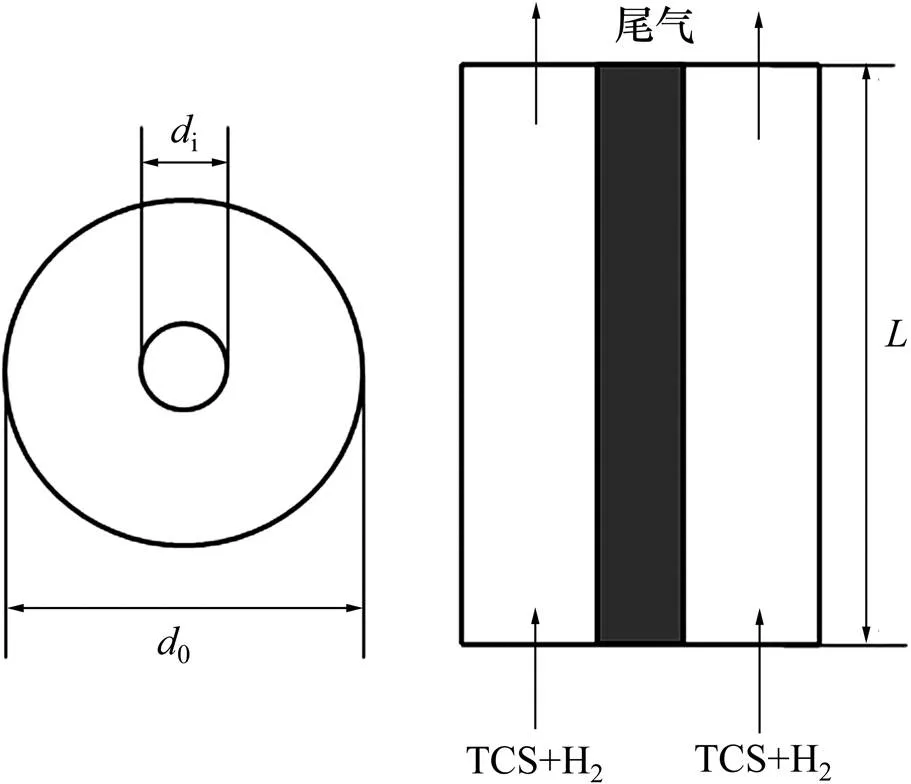
图1 西门子反应器模型几何机构
硅棒表面的化学物质的浓度与进料时不同,因此要考虑传递现象对硅沉积率的影响。AGER等[21−22]对该过程的传递现象进行建模,并提出以下假设:忽略轴向传递、稳态、层流、理想气体、气体特征与化学物质的质量分数无关、忽略热扩散、压强为定值。值得注意的是,尽管硅沉积在硅棒表面会引起硅棒的半径增大,从而导致模型的几何结构发生变化,但是过程的热传递过程的速度要远远大于硅棒的生长速度,因此可以认为该过程为一个稳态过程。但是由于靠近硅棒表面的气体的温度要明显高于外部的气体温度,且有一个温度边界层,导致热扩散不可忽略。并且由于硅棒表面化学反应的发生,且气相温度梯度的存在,气体的轴向传递不可以忽略。因此本文对模型的研究依然保留以下有效假设:稳态、层流、理想气体、气体特征与化学物质的质量分数无关和压强为定值。但是相比已存在的模型,本模型考虑了气体的轴向传递和热扩散现象。传递现象模型的研究原理图见图2。由图2可知:模型主要包括硅棒、气相和隔绝层。传递现象主要分为两大模块,一个模块是硅棒模块,另一个为气相模块。其中硅棒模块包括硅棒的电加热、硅棒与反应器壁的辐射热传递和硅棒与气相的对流热传递。本文重点建立气相模块,包括硅棒与气相的质量传递、动量传递和热传递。由于气相温度与反应器壁温度的差别很小,因此可忽略气相与反应器壁的辐射热传递。
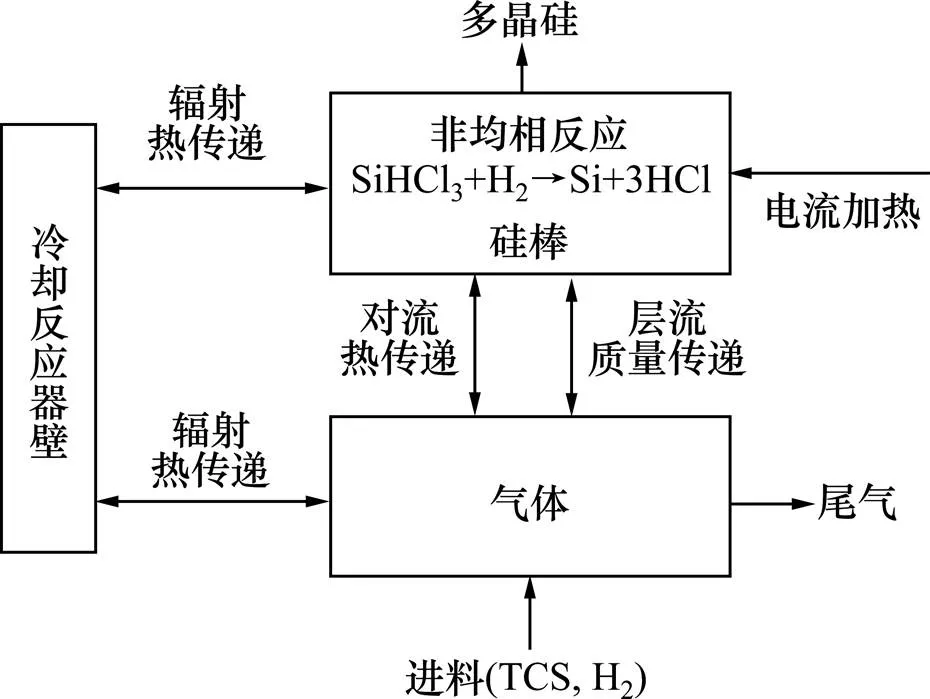
图2 西门子反应器传递现象模型原理图
2 传递−动力学模型
2.1 动量传递
西门子反应器内部的混合气体的速度分布可通过质量守恒方程和动量守恒的方法得到,应用到稳态的圆柱坐标可得:
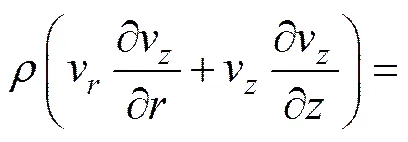
(1)
(2)
其中:为密度;v和v分别为方向和方向的速度;为压强;为重力加速度。
由式(1)可知:此时仍没有令压强为常数。由于温度分布和单个物质的速度和空间分布决定混合物的密度分布,因此需要结合能量守恒方程和单个物质的质量守恒方程,才能确定反应器内部的混合气体的速度分布。式(2)的边界条件为:
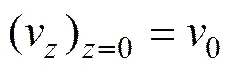
(4)
(5)

由于在硅棒表面的气体速度为0 m/s,因此气体存在速度边界层,速度边界层与温度边界层具有相互影响和制约的关系,两者的关系取决于普朗特常数()。=/=cμ/k,为动力黏度;c为等压比热容;为热导率;为热扩散系数,为运动黏度。由于硅表面的温度较大,在温度边界层内部的气体发生均相反应,从而会在边界层内形成硅粉。然而由于混合气体的黏度很小,边界层很薄,所以本模型忽略均相反应,不考虑硅粉的生成。
2.2 热量传递
该模型设定压强为定值、稳态。稳态圆柱坐标热量守恒方程可表示为

式(7)的边界条件为:
1) 硅表面气体的温度等于硅的表面温度s。
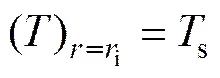
2) 隔绝层处的气体温度等于气体的初始温度。因为在温度边界层以外的气体温度是均匀的,并且温度边界层很小,所以在隔绝层处的温度等于气体的初始温度。
(9)
3) 气体在入口处的温度为初始温度。

2.3 化学物质的质量传递
2.3.1 表面化学反应
由热力学研究可知,在西门子反应器内发生的化学反应非常复杂[2]。但是本模型只考虑硅沉积过程的主要化学反应:
SiHCl3+H2=Si+3HCl (11)
HABUKA等[10]在忽略硅被HCl侵蚀(即逆反应)的速率的条件下,研究了反应(11)的动力学。由于该过程忽略了硅被HCl侵蚀的速率,即忽略了反应(11)的逆反应,因此也可认为是正向反应的反应速率。硅的表面摩尔沉积速率为

其中:x为物质(=TCS,H2)的摩尔分数;为总的反应速率常数,取决于TCS的化学吸附速率常数ad和TCS的分解速率常数r。它们具有如下关系:
(13)
ad=2.72×106exp[−1.72×105/()] (14)
r= 5.63×103exp[−1.8×105/()] (15)
值得注意的是,式(14)和式(15)都只是使用于常压条件下。
由于硅表面HCl的存在,因此硅被HCl侵蚀的速率不能忽略。即需要考虑反应(11)的逆反应,逆反应速率常数(−1)可由式(16)计算得到:

其中:eq为反应(11)的平衡常数。
由式(13)和式(16)得:

若把硅的实际生成速率表示为硅的表面沉积速率与硅的侵蚀速率之差,则硅的实际摩尔增长速率(t)为
(18)
其中:HCl为HCl的摩尔分数。
从而可得物质在硅表面的质量反应速率为
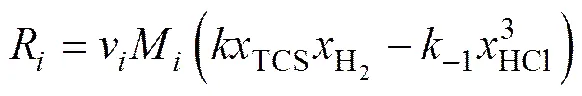
其中:=TCS,H2和HCl;v为化学反应(11)的化学计量数(对于TCS和H2,v=−1;对于HCl,v=3);M为物质的相对分子质量;R为物质的质量反应速率,kg/(m∙s)。
2.3.2 质量传递现象
对于气相中的物质(=TCS,H2和HCl),质量守恒方程为

其中:v为方向的速度;v为方向上的速度;为物质的质量分数;D为物质的扩散系数,可以认为是在H2中的二元扩散系数;为物质的热扩散系数,可由下式计算得到:
(21)
2.3.3 硅沉积速率限制因素选择
硅的沉积速率是由化学反应速率或(和)传递过程控制,为了明确描述硅的沉积过程的速率控制因素,引入“传递−化学反应”速率限制因子(TR),其为气相向硅棒表面最大传递速率与最大表面化学反应速率的比值:
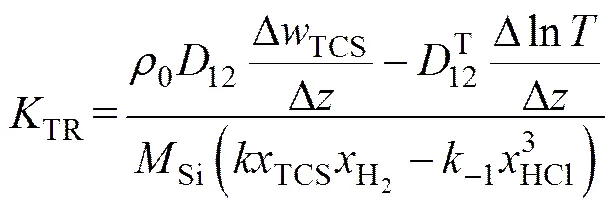
其中:
(23)
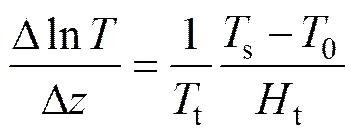
式中:t为气相的参考温度,可由(s−0)计算得到;t为气体流动的参考高度;为在温度为t时的混合气体密度;12为在温度为t时的TCS-H2二元扩散系数;为在温度为t时的TCS-H2二元热扩散 系数。
由式(22)可知:1) 当TR>>1时,硅沉积速率由表面化学反应速率限制。2) 当TR<<1时,硅沉积速率由扩散过程限制。3) 当TR≈1时,硅沉积速率同 时受表面化学反应速率和传递过程控制。HABUKA等[7, 9−13]通过研究发现:当TR>10~50时,硅的增长速率才能趋于饱和,也就是说要保证硅的沉积速率受表面化学反应速率限制,需控制TR>10~50。
而由式(13)可知,表面化学反应速率则由TCS和(或)H2的浓度限制,此时引入sp作为表面化学反应限制因子:

此时应该注意的是,硅的侵蚀速率由生成物HCl的浓度决定。而HCl浓度由表面反应的速率决定,即由硅表面的TCS吸附速率、TCS分解速率以及HCl的传递速率决定。TCS吸附速率由TCS的浓度决定,TCS的分解速率由H2的浓度决定。因此,当反应器中通入的原料配比(即H2的摩尔分数)不同,化学反应速率的限制条件也不同。由式(13)可确定化学反应 因子:
1) 当sp>>1,即>>时,硅表面的TCS浓度很高,则表面化学反应速率由TCS的分解速率限制,即表面化学反应速率只受H2浓度的限制。此时硅的摩尔增长速率为
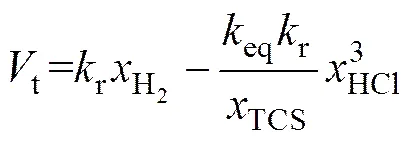
2) 当sp<<1,即<<时,硅表面的H2浓度很高,则表面化学反应速率由TCS的表面吸附速率限制,即表面化学反应速率只受TCS浓度的限制。此时硅的摩尔增长速率为
(27)
3) 当sp处于中间状态时,在数值上与相当,此时表面化学反应速率由TCS的表面吸附速率和TCS的分解速率共同决定,即表面化学反应速率由H2浓度和TCS浓度共同决定。此时硅的摩尔增长速率为
(28)
当sp=5时,认为sp>>1;当1/sp=5时,认为sp<<1;当1/5<sp<5时,认为处于中间状态。而实际生产过程中,进料的配比往往使得化学反应速率的限制条件处于中间状态。
2.3.4 质量传递边界条件
通过以上分析可知,根据传递和化学反应速率的不同,式(12)具有4种不同的硅增长速率限制条件:传递过程限制、氢气浓度限制、TCS浓度限制和氢气与TCS浓度共同限制。
1) 类型1:传递限制。
①进口处物质的质量分数等于通入时的质量分数:
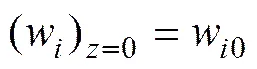
② 在隔绝层处没有质量传递:
(30)
③在硅棒表面的径向扩散通量等于TCS的扩散速率:
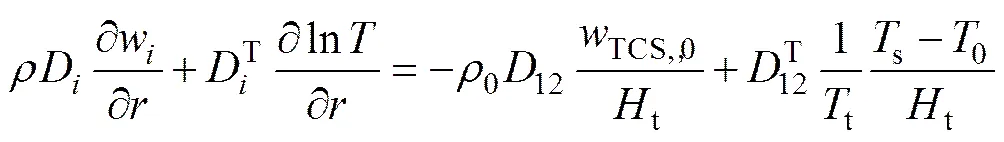
2) 类型2:氢气浓度限制。
①进口处物质的质量分数等于通入时的质量分数:
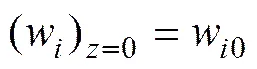
② 在隔绝层处没有质量传递:
(33)
③ 在硅棒表面的径向扩散通量等于物质的消耗量:
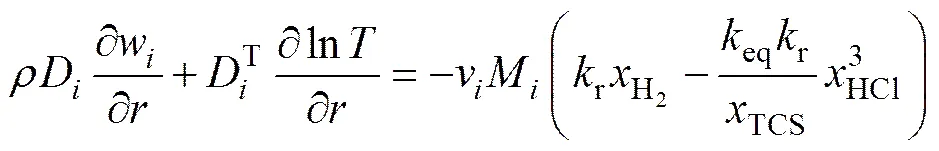
3) 类型3:TCS浓度限制。
①进口处物质的质量分数等于通入时的质量分数:
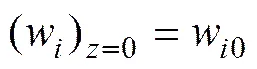
② 在隔绝层处没有质量传递:
(36)
③ 在硅棒表面的径向扩散通量等于物质的消耗量:

4) 类型4:氢气和TCS浓度共同限制。
①进口处物质的质量分数等于通入时的质量分数:
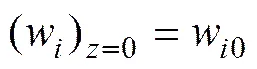
②在隔绝处没有质量传递:
(39)
③在硅棒表面的径向扩散通量等于物质的消耗量:
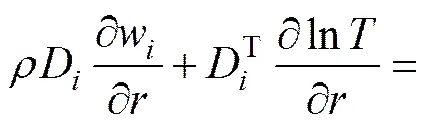
(40)
3 计算结果与分析
气体的流动类型可由气体在反应器进口处的雷诺数(Reynolds number)确定,雷诺数()的定义为

根据表1所示的反应器数据,可得到传递−动力学模型的基本参数,见表2。

表1 反应器的基本参数

表2 传递−动力学模型基本参数
由式(28)可计算硅在硅棒表面单位时间和单位面积的增长速率为
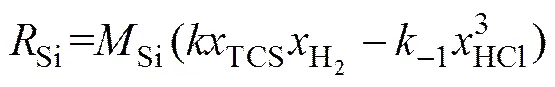
从而可得到硅在硅棒表面的沉积速率为
(43)

图3 TKM模型计算结果与Habuka实验结果[7]及Coso模型计算结果[18]比较
TKM模型的计算结果与Habuka所测得的实验数据[7]以及Coso模型的计算结果[18]进行比较,结果见图3。用平均相对误差来衡量计算值与实验测得值的接近程度,得相对误差仅为3.6%,说明该模型的计算结果与实验结果吻合。并且与Coso模型的计算结果相比,本模型的计算结果明显优于Coso模型的计算结果,见图3。由此可知该模型计算结果的准确性可靠,并优于Coso模型。
随着硅棒表面温度的升高,反应速率逐渐增 大[10]。如果保持进料流量不变,硅沉积过程逐渐由反应速率控制转向由传递过程控制。所以在还原炉启动过程中,随着硅棒表面温度的逐渐升高,进料流量应逐渐的增大。随着硅在硅棒表面的沉积,导致硅棒表面积的增大。由于生产过程中控制硅棒表面温度为一个固定值,会导致硅的沉积量增大,因此在生产过程中,随着硅棒的增长,需要增大进料流料。KTM模型的计算结果可以控制还原炉启动过程进料流量,以及随着硅棒生长,进料流量的变化。
根据模型发展过程可知:硅棒表面温度、进料温度、压强会对硅在硅棒表面的沉积速率产生很大的影响。并且进料配比()会影响化学反应控制条件的转化。当逐渐增大时,化学表面反应会由表面化学吸附限制转向与TCS的热分限制。所以在生产过程中,要选择合理的。应用本文发展的传递−动力学模型可以有效地预测硅表面温度、进料温度、压强、进料配比、进料流量等因素对硅沉积速率的影响,为工业化生产及操作条件优化提供可靠的依据。
4 结论
1) 在合理的假设条件下,本文提出了多晶硅化学气相沉积的传递−动力学模型。该模型即考虑了表面反应和传递现象对硅沉积速率的影响,又考虑了改良西门子法生产过程的副反应。
2) 为了验证模型的准确性,应用多晶硅化学气相沉积的传递−动力学模型计算了一定条件下的硅沉积速率,计算结果与实验数据的相对误差为3.6%,表明传递−动力学模型的计算结果可靠。并与Coso模型比较,传递−动力学模型的计算结果更优。
3) 应用多晶硅化学气相沉积的传递−动力学模型可以有效的预测硅表面温度、进料温度、压强、进料配比、进料流量等因素对硅沉积速率的影响,为工业化生产及操作条件优化提供可靠的依据。
致谢:
感谢美国圣路易斯华盛顿大学的Palghat A Ramachandran教授和Mike Dudukovic教授在多晶硅化学气相沉积的传递−动力学模型发展过程中的讨论。
参考文献:
[1] 侯彦青, 谢刚, 陶东平, 等. 太阳能级多晶硅生产工艺[J]. 材料导报, 2010, 24(13): 31−34, 43. HOU Yanqing, XIE Gang, TAO Dongping, et al. Production technology of solar-grade polycrystalline silicon[J]. Materials Review, 2010, 24(13): 31−34, 43
[2] 侯彦青, 谢刚, 陶东平, 等. SiCl4氢化转化为SiHCl3过程的热力学[J]. 中国有色金属学报, 2011, 21(12): 3202−3210. HOU Yanqing, XIE Gang, TAO Dongping, et al. Thermodynamics of transformation process from SiCl4to SiHCl3[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(12): 3202−3210.
[3] 侯彦青, 谢刚, 陶东平, 等. 锌还原法制备多晶硅过程影响硅产率的因素分析[J]. 北京科技大学学报, 2011, 33(12): 1516−1522. HOU Yanqing, XIE Gang, TAO Dongping, et al. Influencing factors of silicon productivity during production of polycrystalline silicon by zinc reduction process[J]. Journal of University of Science and Technology Beijing, 2011, 33(12): 1516−1522.
[4] HOU Yanqing, XIE Gang, TAO Dongping, et al. Thermodynamic study on zinc reduction process for production of polycrystalline silicon[J]. Journal of Chemical Engineering of Japan, 2011, 44(6): 382−388.
[5] HOU Yanqing, XIE Gang, TAO Dongping, et al. Thermodynamic Study on SiCl4Hydrogenation system in Siemens Process[J]. Journal of Chemical Engineering of Japan, 2011, 44(4): 214−223.
[6] YANG Yongbo. Transport−kinetic effects in manufacture of polycrystalline silicon[D]. ST. Louis, USA: Washington University, 1988: 86−113.
[7] HABUKA H, NAGOYA T. Model on transport phenomena and epitaxial growth of silicon thin film in SiHCl3-H2system under atmospheric pressure[J]. Journal of Crystal Growth, 1996, 169: 61−72.
[8] FALLER F, HURRLE A. High-temperature CVD for crystalline silicon thin film solar cells[J]. IEEE transactions on electron devices, 1999, 46: 2048−2054.
[9] HABUKA H, KATAYAMA M. Nonlinear increase in silicon epitaxial growth rate in a SiHCl3-H2system under atmospheric pressure[J]. Journal of Crystal Growth, 1997, 182: 352−362.
[10] HABUKA H, AOYAMA Y. Chemical process silicon epitaxial growth in a SiHCl3-H2system[J]. Journal of Crystal Growth, 1999, 207: 77−86.
[11] HABUKA H. Hot-wall and cold-wall environment for silicon epitaxial film growth[J]. Journal of Crystal Growth, 2001, 223: 145−155.
[12] HABUKA H, FUKAYAM S. Formation mechanism of local thickness profile of silicon epitaxial film[J]. Journal of Crystal Growth, 2004, 266: 327−332.
[13] HABUKA H, SUZUKI J. Silicon epitaxial growth process using trichlorosilane gas in a single-wafer high-speed substrate rotation reactor[J]. Journal of Crystal Growth, 2011, 327: 1−5.
[14] 张攀, 王伟文, 董海红. 三氯氢硅和氢气系统中多晶硅化学气相沉积的数值模拟[J]. 人工晶体学报, 2010, 39(2): 494−499. ZHANG Pai, WANG Weiwen, DONG Haihong. Numerical simulation of the chemical vapor deposition of polycrystalline silicon in a trichlorosilane and hydrogen system[J]. Journal of Synthetic Crystals, 2010, 39(2): 494−499.
[15] 管俭, 赖喜德, 刘东旗. 大型多晶硅还原炉的温度场模拟[J]. 机械设计与制造, 2009(4): 95−97. GUAN Jian, LAI Xide, LIU Dongqi. The temperature simulation in large-scale polycrystalline silicon furnace[J]. Machinery Design & Manufacture, 2009(4): 95−97.
[16] 王子松, 黄志军, 覃攀. 西门子CVD还原炉内硅棒生产环境的数值模拟[J]. 人工晶体学报, 2012, 41(2): 507−512. WANG Zisong, HUANG Zhijun, TAN Pan. Numerical simulation of polysilicon pods’s growth environment in Siemens CVD reactor[J]. Journal of Synthetic Crystals, 2012, 41(2): 507−512.
[17] 凌猛, 赖喜德, 刘东旗. 多晶硅还原炉炉膛内的辐射传热模型研究[J]. 机械设计与制造, 2009(4): 125−127. LING Meng, LAI Xide, LIU Dongqi. The research of the radiative heat transfer models for the hearth inside polycrystalline silicon reduction furnace[J]. Machinery Design & Manufacture, 2009(4): 125−127.
[18] COSO G, CANIZO C, LUQUE A. Chemical vapor deposition model of polysilicon in a trichlorosilane and hydrogen system[J]. Journal of the Electrochemical Society, 2008, 155(6): D485−D491.
[19] 张攀, 王伟文, 范军领. 三维还原炉内多晶硅化学气相沉积的数值模拟[J]. 太阳能学报, 2012, 33(3): 511−516. ZHANG Pan, WANG Weiwen, FAN Junling. Numerical simulation of the chemical vapor deposition of polycrystalline silicon in a 3D furnace[J]. Acta Energiae Solaris Sinica, 2012, 33(3): 511−516.
[20] CAVALLOTTI C, MASI M. Kinetics of SiHCl3chemical vapor deposition and fluid dynamic simulations[J]. Journal of Nanoscience and Nanotechnology, 2011, 11: 8054−8060.
[21] AGER J, BEEMAN J. High purity isotopically enriched bulk silicon[J]. Journal of the Electrochemical Society, 2005, 152: 448−451.
[22] HASHINOTO K, MIURA K. Growth kinetics of polycrystalline silicon form silane by thermal chemical vapor deposition method[J]. Journal of the Electrochemical Society, 1990, 137: 1000−1007.
(编辑 杨幼平)
Transport−kinetic model of polysilicon chemical vapor deposition in SiHCl3-H2system
HOU Yanqing1, 2, NIE Zhifeng1, 2, XIE Gang2, 3,MA Wenhui1, 2, DAI Yongnian2, YU Xiaohua2, SONG Dongming2
(1. National Key Laboratory for Clean Application of Complex Non-ferrous Metal Resources, Kunming University of Science and Technology, Kunming 650093, China;2. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology,Kunming 650093, China;3. Kunming Metallurgy Research Institute, Kunming 650031, China)
The transport−kinetic model (TKM) of polysilicon chemical vapor deposition (Poly-Si CVD) in a SiHCl3-H2system was developed. The both aspects of surface reaction kinetics and transport phenomena on silicon deposition rate were taken into account in the TKM. The limiting conditions of transport rate and surface chemical reaction rate were studied. Furthermore, the conditions of hydrogen concentration limitation or SiHCl3(TCS) concentration limitation were investigated by TKM and the conditions of both limitation by hydrogen concentration and TCS concentration were also developed in TKM. In order to verify the TKM valid, the silicon deposition rate in different ratios of H2to TCS were studied by TKM under the conditions of silicon length of 2 m, silicon radium of 10 cm, gas flow rate of 0.67 m/s, surface temperature of 1 398 K and pressure of 0.1 MPa. The results show that by comparing calculated results with the experimental data measured by Habuka in the open literature. The relative error is 3.6%, which confirms the validity of TKM since the relative error is within 10%.
transport−kinetic model; polysilicon; chemical vapor deposition; silicon deposition rate; transport phenomena
10.11817/j.issn.1672-7207.2016.11.002
TF645.3.4
A
1672−7207(2016)11−3627−08
2015−12−29;
2016−04−05
国家自然科学基金资助项目(21566015);云南省应用基础研究资助项目(2015FB126);云南省人才培养基金资助项目(kksy201352109) (Project(21566015) supported by the National Natural Science Foundation of China; Project(2015FB126) supported by the Applied Basic Research Projects of Yunnan Province; Project(kksy201352109) supported by the Personnel Training Funds of Yunnan Province)
侯彦青,副教授,从事化工冶金及冶金过程仿真模拟研究;E-mail: hhouyanqing@163.com

