端曲面齿联轴器的创成原理及设计
林超,赵相路,曾东
端曲面齿联轴器的创成原理及设计
林超,赵相路,曾东
(重庆大学机械传动国家重点实验室,重庆,400044)
根据联轴器工作原理,结合空间坐标变换理论、共轭曲面求解理论及正交非圆面齿轮副传动原理,提出端曲面齿联轴器这一新的结构形式,建立端曲面齿联轴器求解的共轭坐标系,推导端曲面齿联轴器的端曲面参数方程,生成端曲面;结合端曲面齿齿盘的几何参数设计理论,采用“共轭截线投影法”新型齿面生成方法,通过solidworks软件对端曲面齿齿面进行几何求解,获得端曲面齿联轴器的连接齿面及十字轴式端曲面齿万向联轴器的三维实体模型;将端曲面齿联轴器应用于冶金等工程设备中,验证端曲面齿联轴器几何设计方法的正确性和在工程应用中的可行性。
端面齿形;共轭曲面;联轴器;三维建模
端面齿联轴器是用来连接两轴或轴与回转体,传递转矩和运动的一类联轴器。一般的端面齿联轴器由2个端齿盘共同组成,端齿盘是指在与联轴器轴线垂直的平面上,轮齿沿圆周均匀分布的齿形联接元件。端面齿联轴器在大功率动力装置中应用广泛,如大功率铁路机车、大功率离心式压缩机、大型柴油发动机的曲轴、航空和工业用燃气轮机或蒸汽轮机的涡轮转子和压缩机转子等设备。端面齿联轴器最早由Gleason公司提出[1],按照轮齿结构分为弧齿及直齿2种形式。对于弧齿端面齿联轴器,Gleason公司首先介绍了弧齿端齿联轴器几何设计及加工过程,随后研究者提出弧齿端齿盘几何设计及强度计算方法[2]、进行弧齿端齿联轴器的强度分析[3]、弧齿端齿连接螺栓应力状态分析[4]以及弧齿端齿盘的接触分析[5],至今弧齿端齿联轴器的发展已较成熟。对于直齿端面齿联轴器,王全先等[6]推导了直齿端齿盘轮齿强度校核公式,可按照JB/T 3242—1993[7]选取参数进行设计,给出了较恰当的设计方法。唐进元等[8]又进一步提出一种直齿端齿盘几何参数设计方法与相应弯曲强度校核计算公式,该方法优化了端齿盘几何设计。综上所述,现有的端面齿联轴器均为在端平面上布齿的型式,尚没有将曲面上布齿应用于联轴器的研究。为此,本文作者提出端曲面梯形齿联轴器的形式,并与端面梯形齿联轴器进行对比分析。端曲面齿联轴器不同于端面齿联轴器,其端齿盘的轮齿并非均匀分布在与联轴器轴线垂直的平面上,而是呈一定规律分布在类似圆周波形的曲面上。根据曲面共轭理论,该曲面与椭圆齿轮节曲面互为共轭曲面[9],并且其成对运动间的内在联系和相互转换规律符合正交非圆面齿轮副的啮合传动规律。端曲面齿联轴器特殊的轮齿分布形式扩大了轮齿横截面积和接触面积,有效提高了其载荷承载能力。它能以更小的尺寸更好地满足高精度、高承载能力和高生产率的需要。
1 端曲面齿联轴器生成原理
普通的端面齿联轴器,其端齿盘的端齿均匀分布在与联轴器轴线垂直的平面上。该类联轴器工作时产生的载荷和冲击全由端面齿来承受,当端面齿受冲击载荷发生断裂时,联轴器将无法继续工作而引起事故。本文所设计的端曲面齿联轴器能够解决上述问题,并且在对中性、承载能力等方面有大幅度提高。端曲面齿联轴器端齿盘的端齿呈一定规律分布在类似圆周波形的端曲面上。
端曲面齿联轴器的端曲面是基于解析曲面的共轭曲面求解理论,通过共轭运动方程的计算,所求解得出的与椭圆齿轮节曲面相共轭的共轭曲面。然而,仅通过解析曲面的共轭理论不能满足现代设计与加工技术的需要,故本文也利用正交非圆面齿轮副的设计理论对端曲面进行联合求解。
常用的齿形有矩形、梯形、锯齿形和三角形。锯形齿无轴向分力但不便于接合与分离,梯形齿强度较高,冲击小故应用较广,锯齿形齿强度最高但只能传递单方向转矩[10]。本文均采用梯形齿,两类联轴器的原理示意图如图1所示。

(a),(b)分别为端面、端曲面凸缘联轴器;(c),(d)分别为端面齿、端曲面齿联轴器
端曲面齿联轴器的端曲面存在二次承载以及二次对中的特点,故而端曲面齿联轴器具有高承载能力、传动转矩大、高刚性以及自动定心的优势。
2 端曲面的求解方法
解析法求解共轭曲面的一个重要内容就是共轭条件的建立和变换,为此, 建立如图2所示的坐标系。在图2中,母曲面t指椭圆柱齿轮节曲面,共轭曲面指端曲面,坐标系为与母曲面t固结,其绕着的轴逆时针旋转了;坐标系与共轭曲面固结。为辅助动坐标系,其绕着的轴顺时针旋转了,并且和重合;为辅助动坐标系, 其沿着的轴水平移动;为辅助动坐标系,其沿着的轴垂直移动,而后又绕着自身坐标系的轴顺时针旋转了90°。在坐标系中,母曲面t柱坐标方程为

图2 共轭坐标系的建立与变换

(2)
式中:21为由坐标系到的变换中的旋转变换矩阵;为辅助动坐标系绕着2轴旋转的角度。

共轭条件为
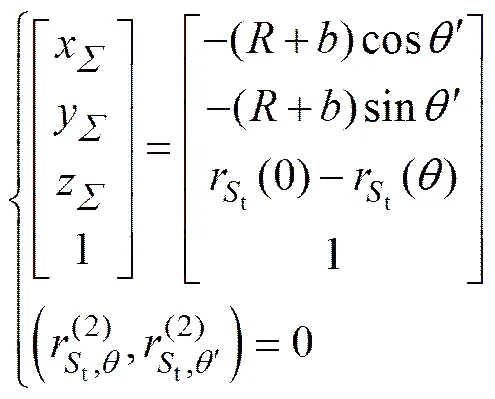
定义2为端曲面的阶数,表示该端曲面在范围内与母曲面t共轭滚动的周期个数。根据端曲面封闭的条件有[11]
(5)
式中:12为正交变传动比面齿轮副传动比。
根据式(1)和式(5)算得,代入式(4)得到端曲面齿联轴器的端曲面参数方程为

取2=2,时,端曲面图形如图3所示,为表达清晰,图中仅显示了端曲面内外边线。可见端曲面随偏心率的增大,波幅会变大,内外径不作改变。端曲面波幅变化会对联轴器的对中性能与端曲面齿压力角等产生影响。
图3 端曲面及偏心率的影响
Fig. 3 Curved-face and influence of eccentricity
3 端曲面齿设计过程
端曲面齿的设计过程就是指将轮齿按照一定规律分布在端曲面上的过程,其造型直接源于正交非圆面齿轮,并采用与其相似的加工方法进行设计。
3.1 几何参数计算
端曲面齿联轴器的齿形结构如图4所示。图4中:1为端曲面齿盘外径;2为内径;为齿宽;为节曲线柱面半径;2为端曲面齿齿数;为齿距;a为齿顶高;f为齿根高。
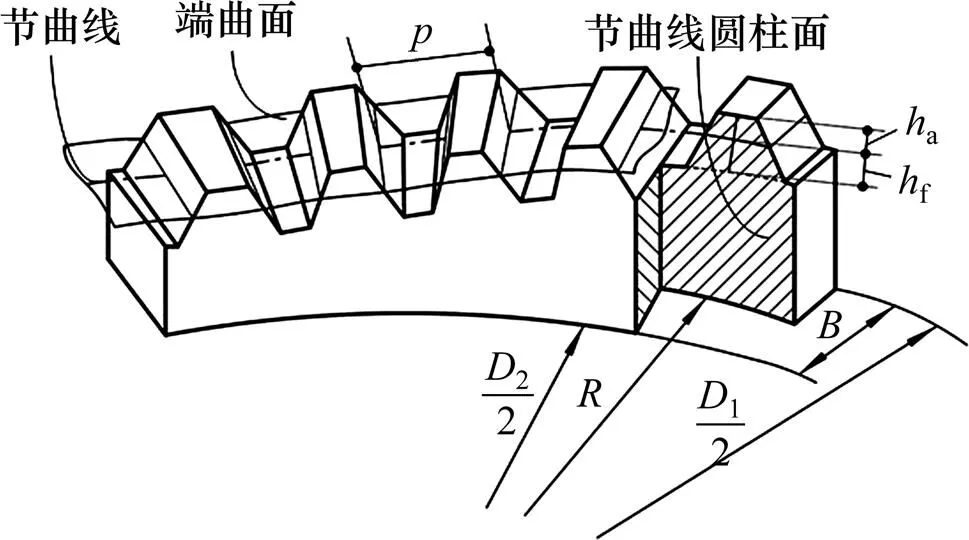
图4 端曲面齿齿形结构示意图
3.1.1 参考直径
利用以下公式[12]初步确定固定式端曲面齿联轴器的尺寸:

式中:为联轴器参考直径;为联轴器转矩。
3.1.2 节曲线柱面半径
由式(5)可知:节曲线柱面半径与椭圆柱齿轮节曲线的关系为

式中:为端曲面齿联轴器的节曲线柱面半径。
结合参考外径尺寸与节曲线柱面半径,选定外径1。在一般情况下,取齿宽为联轴器外径的0.125倍,继而可求出内径2。
3.1.3 端曲面齿齿数2
在选择了端曲齿联轴器的初步尺寸后,就需要确定齿数和齿宽。端曲面齿的模数为,端曲面齿数2与椭圆柱齿轮1的关系为,齿距。
3.1.4 端曲面齿齿顶高a和齿根高f
端曲面齿的齿顶高、齿根高与齿全高的计算公 式[13]如下:

式中:a为端曲面齿齿顶高;f为端曲面齿齿根高;为端曲面齿的模数;为齿顶高系数;为顶隙数。
3.2 端曲面齿齿面几何法求解
3.2.1 共轭截线投影法
共轭截线投影法是指基于共轭曲面求解原理的标杆线汇法的几何化。由于标杆线汇法代数变换和几何变换繁杂,计算工作量大,且计算机不能直接完成。又因为该标杆线汇法的几何转换遵循了正交非圆面齿轮副设计规律,故本文利用母曲面0与共轭曲面1的几何转换关系,并借助solidworks的曲面构建功能,将标杆线汇法进行了几何化表达,形成了一种新的齿面创建方法即共轭截线投影法。共轭截线投影法绕过了传统共轭理论关于共轭曲面必须连续相切接触这一限制,而是着眼于曲面之间真实的接触情况,用标杆射线这一中间媒介的截取来描述曲面之间实际的共轭运动。其基本原理为:先设定母曲面0在其上各点处按既定方向发出“标杆射线”,形成投影线汇。当所求共轭曲面1与投影线汇按已知传动关系进行回转运动时,投影线汇将被共轭曲面1在连续回转下所截取,而投影线汇的所有截线便描述了共轭曲面0。
母曲面0指椭圆齿轮齿面,共轭曲面1指端曲面齿齿面。由图5可进一步了解共轭截线投影法的基本原理和求解方法。图中1和2分别代表单一自、公转角度的“标杆射线”母线;1和2分别代表自、公转方向的投影线汇;1和2分别代表自、公转投影线汇曲面组。
3.2.2 齿面求解过程
为验证本方法的正确性,经几何参数计算方法得出几何参数如表1所示,并以此为例进行端曲面齿齿面的求解。

图5 共轭截线投影法的几何原理
1)几何转换关系确定。根据正交非圆面齿轮副相对运动原理,假设端曲面齿盘毛坯固定,椭圆柱齿轮的节曲面在端曲面上作纯滚动,椭圆柱齿轮的自转角度与公转角度关系[14]如下:
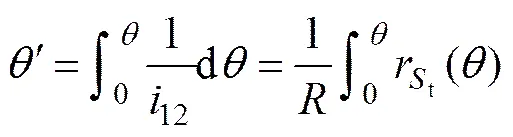
椭圆柱齿轮齿面0绕轴线发出“标杆射线”(完成自转),形成投影线汇。按照以上几何关系确定公转角度,投影线汇将在这些角度内被共轭曲面1所截取。绕端曲面齿盘轴线发出对应各角度的“标杆射线”,形成投影线汇(完成公转),两投影线汇曲面组的交线即为被反求出的端曲面齿截线,连接所有截线即完成端曲面齿的齿面求解。
2)“标杆射线”角度区间的确定。取椭圆柱齿轮齿面0的1/4部分,即1/2个齿面作为“标杆射线”的发生曲面,初始相位默认定为长半轴为轴垂直放置、短半轴为轴水平放置。在垂直于椭圆齿轮轴线的平面上,将各单一齿面两端点分别与轴心连线,两连线与轴的夹角即为该单一齿面的“标杆射线”自转角度区间。在该区间内,以一定角度(本文以0.5°)划分出若干各自代表单一自转角度的“标杆射线”母线。分别将自转角度代入式(9)即可求出公转角度区间。
椭圆柱齿轮的齿数为1,模数为,椭圆柱齿轮节曲线在角度内总长度为,其对应的恰好是1个齿距,则应满足如下条件式:

即
(10)
按照几何转换关系式(9),计算出1个周期内各轮齿齿面的“标杆射线”自转角度区间与公转角度区间,如表2所示。
3) 端曲面齿齿面构建。以齿面5为例,设定齿面5为母曲面0,在自转角度区间39.5°~46°内,确定出代表单一自转角度的“标杆射线”母线1。相应地,在端曲面齿底面上公转角度区间21.17°~24.43°内,确定出代表单一公转角度的“标杆射线”母线2。

表1 椭圆齿轮与端曲面齿盘基本几何参数
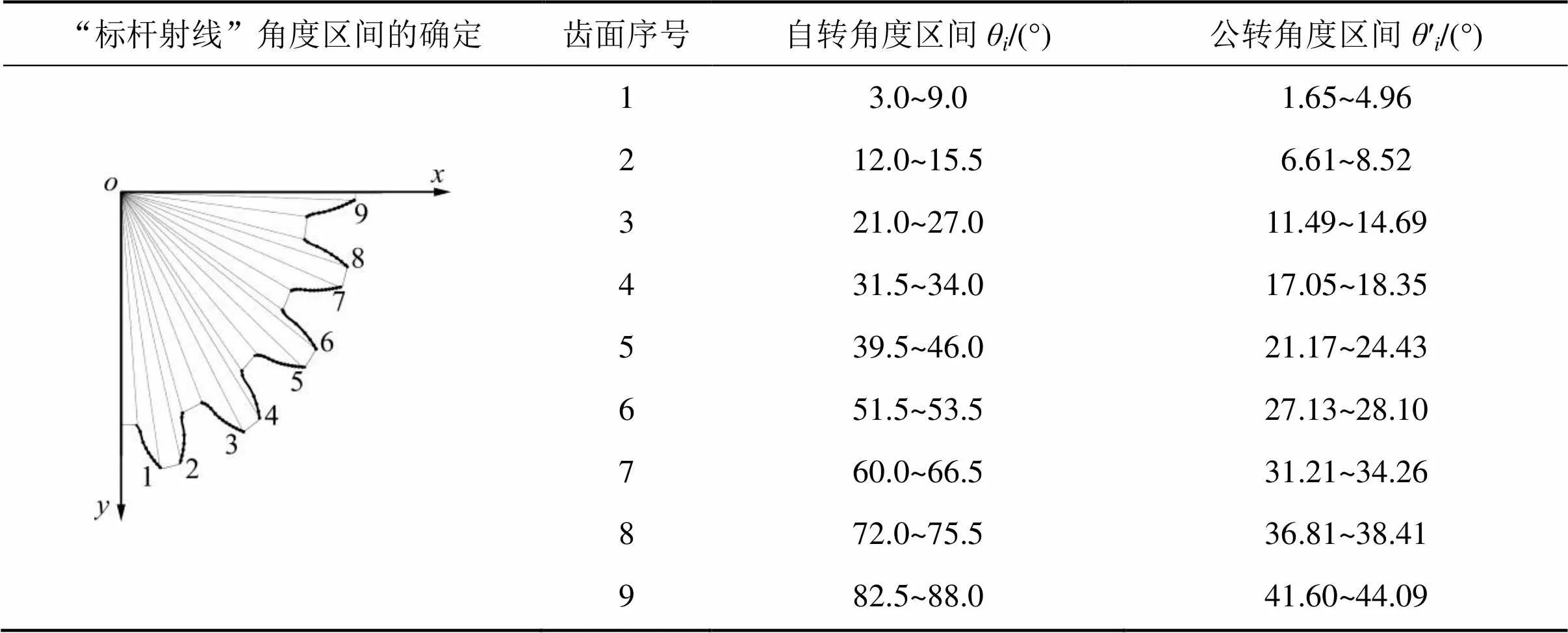
表2 “标杆射线”角度区间
母曲面0上“标杆射线”母线1按自转方向发出“标杆射线”,形成投影线汇1。投影线汇1绕2轴回转,形成自转投影线汇曲面组1。共轭曲面(端曲面齿齿面)1上“标杆射线”母线2按公转方向发出“标杆射线“,形成投影线汇2。投影线汇2沿2轴拉伸,形成公转投影线汇曲面组2。1与2中的曲面一一对应,两投影线汇曲面组的交线即为被反求出的端曲面齿截线,而所有的端曲面齿截线便描述了与齿面5相共轭的端曲面齿齿面5。
按此曲面构建规律,依据表2数据,将其余齿面进行成形操作,可得出1个周期内各个端曲面齿的齿面,如图6所示。随后,对求得的1个周期的齿面进行镜像与圆周阵列等操作,即可得到完整的端曲面齿齿面。

图6 1个周期内端曲面齿的齿面
4) 端曲面齿齿盘成形。所得的端曲面齿齿面为接触齿面,以该接触齿面为分割面对齿盘毛胚进行分割,得到凸凹两端齿盘。在solidworks环境下的具体操作为:在齿盘底端面上绘制内外圈草图,拉伸到接触齿面得一端齿盘;在另一方向齿盘底端面上绘制内外圈草图,拉伸到接触齿面得另一端齿盘。最终得出的端曲面齿齿盘如图7所示。在传递同样扭矩时(本文为40 kN∙m),利用ANSYS软件的workbench版块,将端面梯形齿万向联轴器与端曲面梯形齿万向联轴器的端齿盘进行有限元对比分析,如图8所示。

图7 端曲面齿联轴器端齿盘

(a),(b)分别为端面、端曲面梯形齿弯曲应力;(c),(d)分别为端面、端曲面梯形齿弯曲应变
4 端曲面齿万向联轴器的建模与分析
十字轴式万向联轴器能广泛应用于冶金、起重、工程运输、矿山、石油、船舶、煤炭、橡胶、造纸机械及其他重机行业的机械轴系中传递转矩[15]。将端曲面齿该连接方式应用于万向联轴器的话,将大幅度提高其承载能力、对中性能和传动转矩,并能够有效缩小联轴器体积。下面应用solidworks对该端曲面齿万向联轴器进行三维建模设计。
设计用于冶金等工程设备的十字轴式端曲面齿万向联轴器,传递的最大扭矩为40 kN∙m,根据端曲面齿联轴器几何参数的设计方法,得到该联轴器的几何参数如下:参考外径为164.22 mm,节曲线柱面半径计算值为=77.21 mm,取外径为=180 mm,取端曲面齿模数=4;齿盘阶数2=2,齿数2=36;全齿高2=9 mm;齿顶高a2=4 mm;齿根高f2=5 mm。在传递同样扭矩(40 kN∙m)时,2类万向联轴器的结构参数与有限元对比结果如表3所示。

表3 2类万向联轴器对比
端曲面齿万向联轴器能够以更小的体积来承受同样的扭矩,有利于节约生产成本;端曲面齿存在二次承载以及二次对中的特点,进而提高了载荷承载能力和对中性能,同时具有了自动定心的作用;ANSYS对比分析得出端曲面梯形齿的齿根强度相比于端面梯形齿提高了20%;端曲面梯形齿的变形量和变形程度相比于端面梯形齿小而均匀;前者存在周期性局部应力集中,而后者的应力集中分布在整体齿面。
按计算得出的几何参数,利用solidworks软件对端曲面齿万向联轴器进行三维建模,如图9所示。
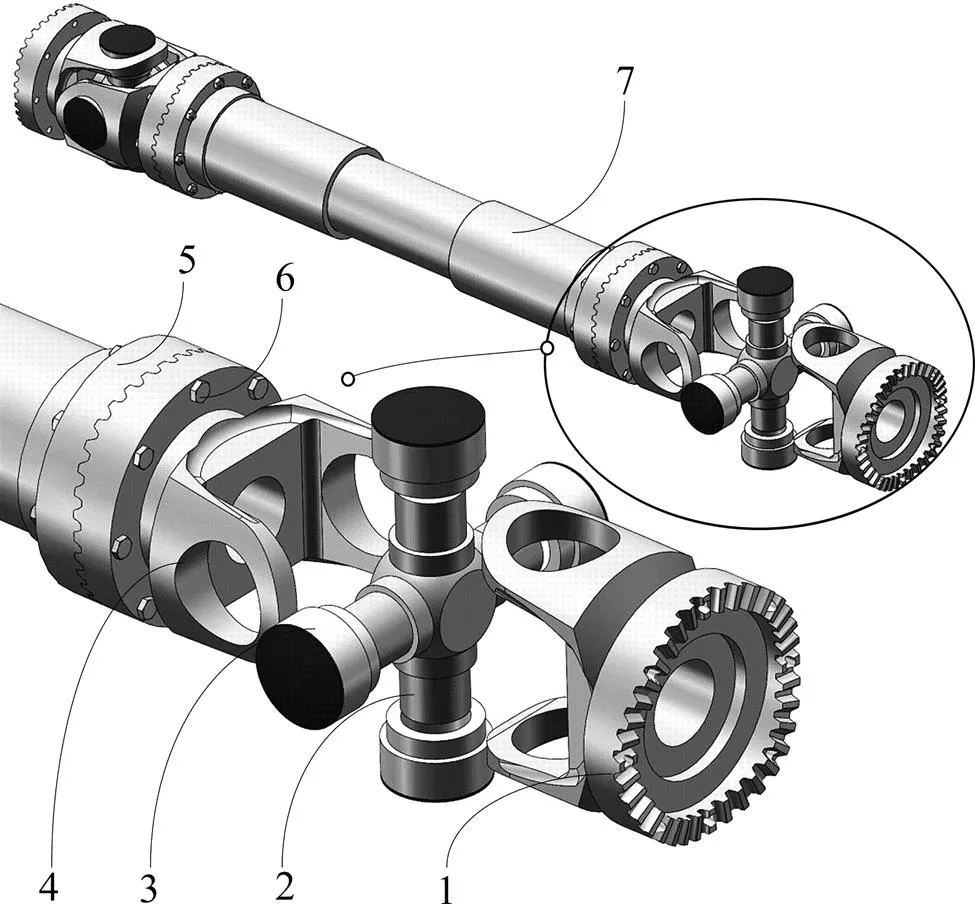
1—端齿凸齿盘;2—十字轴;3—滚子轴承;4—凸齿法兰叉头;5—端齿凹齿盘;6—螺栓;7—连接轴。
5 结论
1) 提出了端曲面齿联轴器这一新的结构形式,建立了端曲面齿联轴器求解的共轭坐标系,通过曲面共轭求解方法推导出了端曲面齿联轴器的端曲面参数方程,生成了端曲面,使得轮齿分布在端曲面上成为可能。
2) 结合端曲面齿联轴器的几何参数设计理论,采用“共轭截线投影法”新型齿面生成方法,通过solidworks软件对端曲面齿齿面进行几何求解,获得了端曲面齿联轴器的连接齿面及三维实体模型。
3) 可以将端曲面齿联轴器应用于冶金等工程设备中,验证了端曲面齿联轴器几何设计方法的正确性和在工程应用中的可行性。
参考文献:
[1] 北京齿轮厂. 格利森锥齿轮技术资料译文集(第2分册)[M]. 北京: 机械工业出版社, 1983: 141−143. Beijing Gear Works. Gleason bevel gear technical data (The second volume)[M]. Beijing: Mechanical Industry Press, 1983: 141−143.
[2] DEMIN A I. Calculation and design of curvic couplings[J]. Mach Tool, 1978, 49(1): 27−30.
[3] PISANI S R, RENCIS J J. Investigating CURVIC coupling behavior by utilizing two-and three-dimensional boundary and finite element methods[J]. Engineering Analysis with Boundary Elements, 2000, 24(3): 271−275.
[4] RICHARDSON I J, HYDE T M. Three-dimensional finite element investigation of the bolt stresses in an aero-engine curvic coupling under a blade release condition[J]. Journal of Aerospace Engineering, 2000, 214(4): 231−245.
[5] BRADLEY J N. Digital inspection of fixed curvic coupling contact pattern[D]. California: California Polytechnic State University, 2012: 23−30.
[6] 王全先, 叶宁军, 汤伟. 联轴器法兰端面齿的设计及有限元分析[J]. 机械设计, 2011, 28(11): 43−46. WANG Quanxian, YE Ningjun, TANG Wei. Design and finite element analysis on the end surface teeth of coupling flange[J]. Journal of Machine Design, 2011, 28(11): 43−46.
[7] JB/T 3242—1993, SWZ型整体轴承座十字轴式万向联轴器[S]. JB/T 3242—1993, SWZ The overall bearing cross shaft universal coupling[S].
[8] 唐进元, 雷敦财, 刘向东, 等. 直齿端齿盘设计研究[J]. 机械设计, 2013, 30(12): 6−11. TANG Jinyuan, LEI Duncai, LIU Xiangdong, et al. Design study for straight end-toothed disc[J]. Journal of Machine Design, 2013, 30(12): 6−11.
[9] 肖来元, 廖道训, 易传云. 共轭曲面求解理论与方法研究[J]. 机械科学与技术, 2002, 21(3): 345−347. XIAO Laiyuan, LIAO Daoxun, YI Chuanyun. An overview of the theory and method on the conjugate surface design[J]. Mechanical Science and Technology, 2002, 21(3): 345−347.
[10] 濮良贵, 纪名刚. 机械设计[M]. 第8版. 北京: 高等教育出版社, 2006: 343−356. FU Lianggui, JI Minggang. Mechanical design[M]. 8th ed. Beijing: Higher Education Press, 2006: 343−356.
[11] 龚海. 正交非圆面齿轮副的传动设计与特性分析[D]. 重庆: 重庆大学机械工程学院, 2012: 10−13. GONG Hai. Transmission design and characteristic analysis of orthogonal non-circular face gear drive[D]. Chongqing: Chongqing University. College of M echanical Engineering, 2012: 10−13.
[12] 黄登红, 曾韬. 固定式端面弧齿连轴节的设计[J]. 机械设计与研究, 2013, 29(1): 31−34. HUANG Denghong, ZENG Tao. Design method for fixed curvic coupling[J]. Machine Design & Research, 2013, 29(1): 31−34.
[13] 吴序堂, 王海贵. 非圆齿轮及非匀速比传动[M]. 北京: 机械工业出版社, 1997: 34−40. WU Xutang, WANG Haigui. Non-circular gear and non uniform than transmission[M]. Beijing: Mechanical Industry Press, 1997: 34−40.
[14] 林超, 李莎莎, 龚海. 正交变传动比面齿轮的设计及三维造型[J]. 湖南大学学报(自然科学版), 2014, 41(3): 49−55. LIN Chao, LI Shasha, GONG Hai. Design and 3D Modeling of orthogonal variable transmission ratio face gear[J]. Journal of Hunan University (Natural Sciences), 2014, 41(3): 49−55.
[15] 贾敬平. 重载十字轴式万向联轴器的运动仿真及结构优化[D]. 合肥: 合肥工业大学, 2013: 1−5. JIA Jingping. Overloading the cross shaft universal coupling motion simulation and structure optimization[D]. Hefei: Hefei University of Technology, 2013: 1−5.
(编辑 陈爱华)
Constructing principle and design of curved-face gear coupling
LIN Chao, ZHAO Xianglu, ZENG Dong
(The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)
According to the working principle of coupling, spatial coordinate transformation theory, solving theory of conjugate curved surface and the drive principle of curved-face gear, the new structure of the curved-face gear coupling was put forward. The conjugate system of the curved-face gear coupling was established. The parameter equation of the curved-face of the curved-face gear coupling was deduced. According to the geometrical parameter design of curved-face gear coupling theory, the method of conjugate cutting line projection was used to generate the tooth surface. A geometrical mathematical model was built to solve the curved-face gear coupling through the solidworks, which can get the tooth surface and of the curved-face gear coupling 3-D entity model. The applications in the field of engineering facility, such as metallurgy etc, were put forward. The advantages of the curved-face gear coupling in engineering application were verified.
transverse tooth profile; conjugate curved surface; coupling; 3-D modeling
10.11817/j.issn.1672-7207.2016.11.013
TH133.4
A
1672−7207(2016)11−3707−08
2016−02−20;
2016−04−27
国家自然科学基金资助项目(51275537) (Project(51275537) supported by the National Natural Science Foundation of China)
林超,教授,博士生导师,从事传动系统创新设计理论与方法、齿轮传动系统的设计、分析与制造研究;E-mail: linchao@cqu.edu.cn

