纳米流体液滴的耗散粒子动力学模拟

沈世元,周哲玮

(上海大学上海市应用数学和力学研究所,上海　200072)

纳米流体液滴的耗散粒子动力学模拟

沈世元,周哲玮

(上海大学上海市应用数学和力学研究所,上海200072)

采用在介观尺度下适用的耗散粒子动力学(dissipative particle dynamics,DPD)方法,对考虑静电力作用的纳米流体系统进行建模,研究了在纳米颗粒带电量和浓度影响下纳米流体液滴接触角的变化.通过对实验过程进行的数值模拟,得到了定性相同的结果.

纳米流体；介观尺度；耗散粒子动力学；极化

2003年,You等[1]基于纳米流体的沸腾热传递(boiling heat transfer,BHT)研究,分析了临界热通量(critical heat flux,CHF)的变化,得到了临界热通量显著升高的结论,但未给出临界热通量升高的原因.这种未能解释的、有趣的现象吸引了大量的科研工作者对纳米流体临界热通量的显著变化进行研究.2005年,Vafaei等[2]制备了纳米颗粒被巯基乙酸功能化的碲化铋纳米流体,并发现纳米流体液滴的接触角与纳米颗粒的浓度及尺寸有关.2006年,Kim等[3]分别用3种不同的氧化物颗粒(氧化锆、氧化铝和氧化硅)制备了纳米流体,并对其性质进行了研究,发现在干净的固壁表面上,纳米流体液滴的接触角随浓度变化不大,但是对于壁面上存在沉降的纳米颗粒的情况来说,接触角由于润湿性的增大有明显的减小.2010年,Ahn等[4]通过方腔流实验发现,与纯水相比,纳米流体流过的固壁表面上的临界热通量显著升高.通过对接触角的测量和固壁表面性质的研究,确定临界热通量的升高主要是由纳米颗粒沉降在固壁表面导致的润湿性增大造成的.

对这一现象本课题组进行了研究,多体耗散粒子动力学(many-body dissipative particle dynamics,MDPD)方法的模拟显示,对于悬浮在水中的SiO2纳米颗粒,其浓度对液滴接触角无影响；而沉降在固壁表面的SiO2纳米颗粒数则影响液滴接触角,该结果与Ahn等[4]的实验结果定性符合.Vafaei等[2]指出,在给定的实验条件下,纳米流体液滴的接触角与纳米颗粒的浓度有关,原因是修饰纳米颗粒表面的官能团在水中产生了极化,纳米颗粒与流体的相互作用以及纳米颗粒之间长程的静电作用对纳米流体的毛细管性能产生了影响.本工作主要参考胶体模型,通过带有电荷的耗散粒子动力学(dissipative particle dynamics,DPD)方法模拟纳米流体液滴来研究Vafaei等[2]的实验.

1　DPD方法

1.1标准的DPD方法

1992年,DPD方法由Hoogerbrugge等[5]提出.1998年,Warren[6]认为耗散粒子可以表示分子、原子、高分子蛋白质聚团、带电离子团等,指出了DPD方法的广泛适用性.之后,学者们对于介观尺度下的纳米流体做了一些基于DPD方法的数值模拟工作.2008年,He等[7]利用能量守恒DPD方法模拟了纳米流体的热传导,指出热导率与流体中包含的纳米颗粒数成正比关系,并认为产生这种现象的原因是纳米颗粒的布朗运动.2012年,Yamada等[8]利用能量守恒DPD方法模拟了一维微通道纳米流体的热传导,与实验结果符合较好,并指出纳米流体的流动速度、pH值、纳米颗粒形状都会影响纳米流体的热传导率.目前,利用分子动力学(molecular dynamics,MD)方法研究纳米流体的报道[9-13]较多,但本工作利用DPD方法对纳米流体进行研究.

与MD方法相同,DPD方法采用Lagrange坐标描述粒子,体系中的粒子运动满足牛顿运动方程：

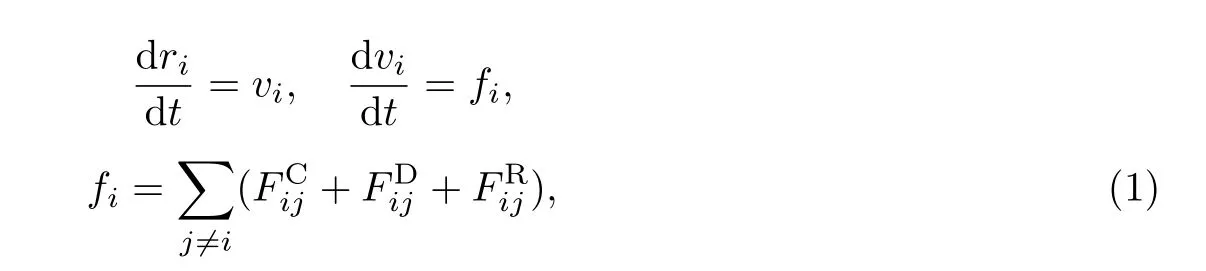
ωC,ωD,ωR为各力的权重函数；rij为i,j粒子间的距离；eij为和rij方向相同的单位矢量；aij为保守力系数,反映粒子i和j之间的最大排斥力；γ和σ分别为耗散力和随机力幅值；vij=vi−vj,θij为高斯白噪声项,满足以下统计学特性：

Espanol等[13]将耗散涨落定理引入耗散粒子动力学方法中,为耗散力和随机力提供了统计热力学上的平衡条件,即

本工作采用Groot等[14]提出的修正的Velocity-Verlet算法：

式中,λ为可调参数.当λ=0.5时,该算法和标准的Velocity-Verlet算法[15]一致.目前,绝大部分DPD模拟都采用这种修正的Velocity-Verlet算法.

在DPD体系中,将单个DPD粒子的质量mi、截断半径Rc和能量kBT选取为系统的参考单位.例如,以水为例,将N0个质量为m的水分子粗粒化为一个DPD粒子,粒子的质量为mi=N0·m,继而可以得到无量纲单位1对应的真实物理长度：

式中,ρD为DPD粒子的数密度,ρ0为水的密度.

通过长度、质量、能量共3个无量纲基本量,可以分别导出速度、时间和力的无量纲量表达式：

式中,kB是玻尔兹曼常数,一般来说,kBT=1.0；M∗=N0×m,即单个DPD粒子的质量.如无特别说明,本模拟中采用的参数均以DPD无量纲单位给出.

1.2改进的DPD算法

在DPD模型中最重要的参数是各种粒子间的保守力参数.Groot等[14]通过维里方程得到了状态方程(equation of state,EOS),并通过算例在数密度足够高(ρD＞2)的前提下得到了保守力参数的近似形式：

式中,a为排斥力系数.标准的DPD方法在介观模拟方面已经取得了很大的成功,而MDPD方法使状态方程中出现密度的高次项,可以解决标准的DPD方法所无法解决的模拟气液共存的问题[14,16].在本工作中,为了模拟气液共存的状态,采用MDPD方法来对液滴进行模拟. MDPD方法是在保留了耗散力、随机力的基础上,通过引入吸引相互作用,对保守力进行了修正.修正后的保守力的表达形式为

rc和rd分别为吸引和排斥截断半径.

Warren[16]改进了状态方程的形式.改进后的状态方程为

式中,α为一个平均场的系数,数值在0.101左右；A,B为系数矩阵；c为密度相关常数,d由10%×cρ2D得出.Warren[16]通过一系列的数值实验,选取了两组参数开展进一步的研究,最终确定了系数矩阵A和B的具体数值.

2　静电相互作用

当DPD粒子带有电荷时,静电相互作用随粒子间距增大而衰减的速度远低于范德华作用,如果对静电势能函数采取直接截断的方式,其截断半径要远大于范德华作用的截断半径,否则将会产生较大的误差.同时,由于DPD粒子的软粒子性质,当一对异性电荷无限接近时,电场力将出现奇异性,导致人工离子对的产生.为了避免上述这些问题,当采用DPD模拟静电相互作用时,粒子所带电荷需要用电荷分布来表示.本工作基于标准Ewald求和法和分布电荷来求解静电力.

在求解静电相互作用时,相关参数的取值参考文献[17].对于本工作中长方体的计算域的算例,采用Ewald求和法求解DPD模型中两个带电粒子之间的作用力,结果如图1所示.可以看出,计算结果与理论结果吻合较好.同时也可以看出,DPD模型中的静电力也是软作用力,在两个DPD粒子质心距离r＜1的部分有定义说明DPD粒子之间可以相互侵入.

图1　DPD模型中两个带电粒子间的作用力Fig.1　Interaction force between two particles in DPD model

3　建模与计算

3.1建模

在带电胶体体系中存在双电层结构,该结构对胶体颗粒的稳定性起到决定性作用.20世纪40年代,前苏联学者Derjaguin等[18]与荷兰学者Verwey等[19]分别独立地提出了各种形状的胶体颗粒间相互吸引能与双电层排斥能的计算方法,并对胶体体系的稳定性进行了定量描述,即描述胶体体系稳定性的DLVO(Derjaguin-Landau-Verwey-Overbeek)理论.DLVO理论认为,胶体颗粒间同时存在着范德华吸引作用和双电层引起的静电排斥作用,并且体系的稳定性取决于胶体颗粒之间吸引作用和排斥作用的相对大小.

MDPD程序采用的参数如表1所示,其中参数均以无量纲单位给出.

表1　MDPD程序的参数取值Table 1　Parameters selection of MDPD program

3.2计算

在实验中,被巯基乙酸功能化的Bi2Te3纳米流体,可通过改变Bi2Te3颗粒的浓度来改变接触角的大小.在数值模拟中,不仅要考虑改变纳米颗粒的浓度大小,由于体系极化程度与纳米颗粒带电量的关系还不清楚,因此还需要考虑改变纳米颗粒带电量大小.

对于带电量Q的设置,只需要在程序中赋值即可.对于浓度的改变,有两种方案：①调整纳米颗粒数,从50开始,增量为50,增加到350为止,以使浓度逐渐增加；②调整初始液滴半径R,R越大,纳米流体的浓度就越小,但是缺点是计算成本会相应增加.

黄汝佳等[22]对于纯水与固壁组成的系统,给出了MDPD方法中液体与固壁相互吸引力作用系数A12与接触角θ的函数关系：θ=5.5046A12+228.98(见图2),并介绍了计算接触角的圆拟合算法.本工作采用圆拟合算法来计算接触角.由于吸引力作用系数A12对接触角的影响比其他Aij要大得多,在文献[22]给出的“自上而下”方法中,可以由实际测量得到的液滴的静态接触角来决定A12,以处理非单纯物质组成的较复杂的实际流体和实际固壁.

图2　纯水与固壁的吸引力作用系数与接触角的关系Fig.2　Relationships between attractive force coefficients and their contact angles

首先选取两个参数：初始接触角θ0、单个纳米颗粒带电量Q,计算纳米颗粒浓度由低到高变化时纳米流体液滴接触角的变化,并与文献[2]中的实验数据进行对比,结果如表2和图3所示.由图3可以看出,随着纳米颗粒浓度V的增大,纳米液滴接触角θ呈先增大后减小的趋势.

表2　数值模拟结果与文献[2]中实验数据的对比(R=14,Q=8,25)Table 2　Comparisons of numerical simulation with experimental results in Ref.[2](R=14,Q=8,25)

接下来,分析各种参数情况下纳米颗粒浓度和带电量的改变对接触角的影响.由于圆拟合算法对于接近钝角的计算相对更加准确,所以采用85°的初始接触角.

(1)初始液滴半径R=5.

对于较小的液滴半径进行计算,可在纳米颗粒浓度较高、结果改变明显时分析定性的趋势.当纳米颗粒带电量为1,3,5时,接触角随纳米颗粒浓度的变化如表3和图4所示.

图3　纳米流体液滴的接触角随纳米颗粒浓度的变化Fig.3　Relationships between nanofluid droplet contact angles and nanoparticle concentrations

表3　纳米颗粒带电量Q=1,3,5时,不同纳米颗粒浓度下液滴的接触角(R=5)Table 3　Droplet contact angles for different nanoparticle concentrations when Q=1,3,5(R=5)

当纳米颗粒浓度为1.54%时,纳米流体液滴接触角随纳米颗粒带电量Q的变化如表4和图5所示.

表4　纳米颗粒浓度为1.54%时,液滴接触角随纳米颗粒带电量Q的变化(R=5)Table 4　Droplet contact angles for different nanoparticle charge quantities when V=1.54%(R=5)

图4　纳米颗粒带电量Q=1,3,5时,液滴接触角随颗粒浓度的变化(R=5)Fig.4　Droplet contact angles for different nanoparticle concentrations when Q=1,3,5(R=5)

图5　纳米颗粒浓度V=1.54%时,液滴接触角随纳米颗粒带电量Q的变化(R=5)Fig.5　Droplet contact angles for different nanoparticle charge quantities when V=1.54%(R=5)

(2)初始液滴半径R=7.4.

当纳米颗粒带电量为1,3,5时,液滴接触角随纳米颗粒浓度的变化如表5和图6所示.

表5　纳米颗粒带电量Q=1,3,5时,不同纳米颗粒浓度下液滴的接触角(R=7.4)Table 5　Droplet contact angles for different nanoparticle concentrations when Q=1,3,5(R=7.4)

图6　纳米颗粒带电量Q=1,3,5时,液滴接触角随纳米颗粒浓度的变化(R=7.4)Fig.6　Droplet contact angles for different nanoparticle concentrations when Q=1,3,5(R=7.4)

当纳米颗粒浓度为0.62%时,纳米流体液滴接触角随纳米颗粒带电量Q的变化如表6和图7所示.

表6　纳米颗粒浓度V=0.62%时,液滴接触角随纳米颗粒带电量Q的变化(R=7.4)Table 6　Droplet contact angles for different nanoparticle charge quantities when V=0.62%(R=7.4)

图7　纳米颗粒浓度为0.62%时,液滴接触角随纳米颗粒带电量Q的变化(R=7.4)Fig.7　Droplet contact angles for different nanoparticle charge quantities when V=0.62%(R=7.4)

(3)初始液滴半径R=14.

当纳米颗粒带电量为1,20时,液滴接触角随纳米颗粒浓度的变化如表7和图8所示.当纳米颗粒浓度为0.07%时,液滴接触角随纳米颗粒带电量Q的变化如表8和图9所示.

表7　纳米颗粒带电量Q=1,20时,不同纳米颗粒浓度下的液滴接触角(R=14)Table 7　Droplet contact angles for different nanoparticle concentrations when Q=1,20(R=14)

图8　纳米颗粒带电量Q=1,20时,液滴接触角随纳米颗粒浓度的变化(R=14)Fig.8　Droplet contact angles for different nanoparticle concentrations when Q=1,20(R=14)

表8　纳米颗粒浓度V=0.07%时,液滴接触角随纳米颗粒带电量Q的变化(R=14)Table 8　Droplet contact angles for different nanoparticle charge quantities when V=0.07%(R=14)

图9　纳米颗粒浓度为0.07%时,液滴接触角随纳米颗粒带电量Q的变化(R=14)Fig.9　Droplet contact angles for different nanoparticle charge quantities when V=0.07%(R=14)

综上所述,可以得出以下结论：

(1)纳米颗粒带电量较大时(Q＞20),液滴接触角最大值在颗粒浓度为0.5%附近.当纳米颗粒浓度小于0.5%时,随着颗粒浓度的增加,纳米流体液滴的接触角缓慢增大,趋势较不明显；当纳米颗粒浓度大于0.5%时,随着颗粒浓度的增加,纳米流体的接触角逐渐减小.

(2)纳米颗粒带电量较小(Q=1)时,无论颗粒浓度如何变化,液滴接触角的变化趋势都不明显.

(3)纳米颗粒浓度较高(V＞0.5%)时,液滴接触角最大值在Q=4附近.随着颗粒带电量的增大,液滴接触角呈现先增大后减小的趋势.

3.3进一步探讨

进一步分析液滴半径R=5的算例.为了观察纳米流体液滴(考虑静电相互作用)内部的粒子分布情况,不显示阻碍观察的水的DPD粒子.系统中纳米颗粒和正离子DPD粒子的分布情况如图10所示,其中黑色的是固壁,也就是实验中的基板初始设置固壁带负电.图10(a)中,浅色小球表示水的DPD粒子；图10(b)中,深色小球和浅色小球分别代表液滴内部的纳米颗粒以及正离子的DPD粒子,禁止显示水粒子.由图10可以看出：由于同性相斥,带负电的纳米颗粒受到了来自固壁相斥的作用力而远离固壁；由于异性相吸,带正电的正离子被固壁的库仑力所吸引,沉降到了固壁.

因此,纳米液滴的接触角增大很有可能是因为初始浓度比较低时,纳米流体液滴的顶端被悬浮的纳米颗粒撑高,固壁附近的纳米颗粒被推离壁面,携带附近的流体一起,使得液滴表面朝着接触角变大的方向运动.

图10所示的基板上布置了一层带负电的羟基,可以将其看作双电层中带负电的固壁.根据双电层的机理可知,这层带负电的固壁会吸附带正电的粒子并于附近形成一个Stern层.如果假设固壁带电量是一定的,那么吸附正离子的数量仅取决于纳米流体内部本身的极化程度.纳米颗粒浓度越大,液滴内部游离的正离子也就越多,容易被吸附到固壁上的正离子也就越多.当一定数量的正离子被吸附到固壁上之后,固壁表面的物理性质就会发生变化,主要表现在三相点附近与液滴的相互作用发生了变化.三相点附近物理性质的变化也会影响接触角,使得接触角变小.

图10　纳米流体液滴中纳米颗粒和正离子的分布Fig.10　Distribution for nanoparticles and positive ions in nanofluid droplet

4　结束语

Vafaei等[2]的实验表明,纳米流体液滴的接触角与纳米颗粒的浓度有关,并猜想造成这个现象的原因是修饰纳米颗粒表面的官能团在水中产生了极化,纳米颗粒与流体的相互作用以及纳米颗粒之间长程的静电作用对纳米流体的毛细管性能产生了影响.本工作参考胶体模型,用带有电荷的DPD系统来模拟纳米流体液滴.研究结果表明,该模型可以定性地描述纳米流体液滴的静态接触角随纳米颗粒浓度的增加而呈现先增大后减小的变化趋势.由于颗粒浓度与实验结果还有数量级的差别,说明仅用纳米颗粒携带负电荷和水中布置相应正离子的模型来模拟纳米颗粒被巯基乙酸功能化的碲化铋纳米流体还过于粗糙,需要进一步细化.最后通过分析纳米颗粒在液滴中的分布,探讨了纳米颗粒影响接触角的物理机制.

[1]YOU S M,KIM J H,KIM K H.Effect of nanoparticles on critical heat flux of water in pool boiling heat transfer[J].Applied Physics Letters,2003,83(16)：3374-3376.

[2]VAFAEI S,BORcA-TAScIUc T,PRODOwSKI M Z,et al.Effect of nanoparticles on sessile droplet contact angle[J].Nanotechnology,2006,17(10)：2523-2527.

[3]KIM S J,BANG I C,BUONGIORNO J,et al.Effects of nanoparticle deposition on surface wettability influencing boiling heat transfer in nanofluids[J].Applied Physics Letters,2006,89(15)：153107.

[4]AHN H S,KIM H,JO H J,et al.Experimental study of critical heat flux enhancement during forced convective flow boiling of nanofluid on a short heated surface[J].International Journal of Multiphase Flow,2010,36(5)：375-384.

[5]HOOGERBRUGGE P J,KOELMAN J M V A.Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics[J].Europhysics Letters,1992,19(3)：155-160.

[6]WARREN P B.Dissipative particle dynamics[J].Current Opinion in Colloid&Interface Science, 1998,3(6)：620-624.

[7]HE P,QIAO R.Self-consistent fluctuating hydrodynamics simulations of thermal transport in nanoparticle suspensions[J].Journal of Applied Physics,2008,103(9)：094305.

[8]YAMADA T,ASAKO Y,GREGORy O J,et al.Simulation of thermal conductivity of nanofluids using dissipative particle dynamics[J].Numerical Heat Transfer,2012,61(5)：323-337.

[9]EvANS W,FISH J,KEBLINSKI P.Role of Brownian motion hydrodynamics on nanofluid thermal conductivity[J].Applied Physics Letters,2006,88(9)：093116.

[10]VLADKOv M,BARRAT J L.Modeling transient absorption and thermal conductivity in a simple nanofluid[J].Nano Letters,2006,6(6)：1224-1228.

[11]EApEN J,LI J,YIp S.Mechanism of thermal transport in dilute nanocolloids[J].Physical Review Letters,2007,98(2)：028302.

[12]EApEN J,WILLIAMS W C,BUONGIORNO J,et al.Mean-field versus microconvection effects in nanofluid thermal conduction[J].Physical Review Letters,2007,99(9)：095901.

[13]ESpANOL P,WARREN P.Statistical mechanics of dissipative particle dynamics[J].Europhysics Letters,1995,30(4)：191-196.

[14]GROOT R D,WARREN P B.Dissipative particle dynamics：bridging the gap between atomistic and mesoscopic simulation[J].The Journal of Chemical Physics,1997,107(11)：4423-4435.

[15]ALLEN M P,TILDESLEy D J.Computer simulation of liquids[M].Oxford：Clarendon Press, 1987.

[16]WARREN P B.Vapor-liquid coexistence in many-body dissipative particle dynamics[J].Physical Review E,2003,68(6)：066702.

[17]王永雷.静电相互作用的计算在耗散粒子动力学模拟中的实现及应用[D].长春：吉林大学,2012.

[18]DERjAGUIN B,LANDAU L.Theory of the stability of strongly charged lyophobic sols and the adhesion of strongly charged particles in solutions of electrolytes[J].Acta Physicochim,1941, 14(1)：30-59.

[19]VERwEy E J W,OvERBEEK J T G.Theory of the stability of lyophobic colloids[J].Journal of Colloid Science,1955,10(2)：224-225.

[20]MIAO J,DONG M,REN M,et al.Effect of nanoparticle polarization on relative permittivity of transformer oil-based nanofluids[J].Journal of Applied Physics,2013,113(20)：204103.

[21]HwANG J G,ZAHN M,PETTERSSON L A.Bipolar charging and discharging of a perfectly conducting sphere in a lossy medium stressed by a uniform electric field[J].Journal of Applied Physics,2011,109(8)：084331.

本文彩色版可登陆本刊网站查询：http://www.journal.shu.edu.cn

Dissipative particle dynamics simulation of nanoparticles droplet

SHEN Shiyuan,ZHOU Zhewei
(Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China)

Mesoscale dissipative particle dynamics was used to model a nanofluid system considering electrostatic interaction.The effects on the droplet static contact angle of the concentration and charge quantity of the nanoparticles were investigated.Computational results were qualitatively agreed with experiments.

nanofluid；mesoscale；dissipative particle dynamics；polarization

O 35

A

1007-2861(2016)05-0560-13

10.3969/j.issn.1007-2861.2015.02.015

2015-06-05

国家自然科学基金资助项目(11372175)

周哲玮(1950—),男,教授,博士生导师,博士,研究方向为流体稳定性理论及其应用. E-mail:zhwzhou@shu.edu.cn