两种立方体构型的微泡超声造影剂的温度场

杨青,徐凯宇,2,冯江涛,2

(1.上海大学上海市应用数学和力学研究所,上海　200072；2.上海大学理学院,上海　200444)

两种立方体构型的微泡超声造影剂的温度场

杨青1,徐凯宇1,2,冯江涛1,2

(1.上海大学上海市应用数学和力学研究所,上海200072；2.上海大学理学院,上海200444)

通过计算黏性耗散产生的能量,研究了磷脂薄膜超声造影剂在外界声压激励下,单一微泡在血液环境内的温度场.结合实验观测,构造了以一个红细胞为中心,8个微泡为顶点的正立方体模型,计算了微泡引起的中心温度的增量.对于微泡浓度较高或出现微泡团黏滞在组织机体表面上的情况,提出了密排面心立方体模型,计算了微泡团对矩形区域产生的温度场,得到了在此范围内的最高温度.最后对所提出模型的安全性进行分析,证明了其可行性和有效性.

超声造影剂；耗散能；温度场；正立方体模型；密排面心立方体模型

近年来,超声技术发展十分迅速,并在医学和生物学等领域得到了广泛的应用.例如,高强度聚焦超声利用高温性质捕助治疗各种癌症[1].超声疗法虽然能较好地抑制癌细胞的生长[2],但同时也会对人体组织造成某些伤害[3].在理论研究方面,有关微泡在液体中的振动已经有了较多的讨论.Rayleigh[4]首先提出了球形微气泡处于无限大不可压缩液体中的动力学方程.Plesset[5]在Rayleigh模型的基础上考虑了流体的黏滞性和表面张力,导出了微气泡动力学经典的Rayleigh-Plesset(R-P)方程.此后R-P方程根据不同的环境以及振动模式又得到了多次修正[4].Church[6]结合经典理论导出了有膜壳微泡在流体介质中的R-P方程,证明了增加有膜壳微泡的表面张力更容易保持微泡的稳定性,并通过研究二阶以下的谐频响应,得到单个有膜壳微泡由于膜壳弹性模量的影响而比无膜壳微泡的谐振频率高、散射截面大等结论. Allen等[7]研究了不同膜厚的微泡动力学特性,计算出微泡半径不同对其最大膨胀比的影响,并通过实验观测到由于微泡内外壁速度差造成的微泡瞬间破裂现象[8].

超声波除了能使微泡在空化反应下产生热量以外,还作为一种机械波在振动过程中传递能量[9].判断超声波的标准有2个指数：热指数和机械指数,其中热指数是衡量人体组织器官对超声能量吸收导致温度升高的能力,机械指数是衡量超声经过人体内部产生机械效应的能力[10].医学临床诊断中针对这2个指数明确规定了超声医疗设备的适用范围[11].在合理的范围内利用微泡空化反应达到靶向基因治疗已成为当前研究的重点[12].

本工作利用有膜壳微泡的动力学R-P方程,计算了血液环境下磷脂薄膜微泡通过黏性耗散能产生的温度场,并根据实验观测到的微泡形态构建模型,得到了正立方体和密排面心立方体2种构形下多个微泡产生的温度场,最后根据温升对微泡安全性进行了说明.

1　实验观测和模型

1.1正立方体结构模型

微泡超声造影剂在受到外部超声激励后会释放热量,并将热量传递给周围环境.热量的产生方式主要有3种：①在外部声压的激励下,微泡由于压力的作用收缩使得内部的气体产生热量；②微泡吸收外界辐射的声能产生热量；③微泡振动的过程中由于黏性耗散产生热量.已有研究表明,在超声诊断所控制的超声范围内黏性耗散产生的热量占主导地位[13],因此可通过耗散能量的计算得到一个超声脉冲周期内微泡向周围释放的热量.

在室温条件下,用5 mL、质量浓度为0.9%的氯化钠溶液稀释六氟化硫微泡(SonoVue),然后通过生物显微镜(Mshot ML32)观察,结果如图1所示.可以发现,多个微泡之间距离很接近,甚至有部分微泡黏连在一起.实际上,微泡在血液流动的过程中并不是全部黏连在一起的,并且当微泡稀疏时,其在血液环境中的升温可能会引起红细胞结构的破坏.因此,仅对单个微泡的温度场进行研究是不完善的.由于微泡的分布复杂无序,需对其排布进行理想化处理.假设微泡的分布如同一个正立方体,如图2所示.

图1　生物显微镜下观测到的微泡超声造影剂SonoVueFig.1　Microbubble ultrasonic contrast agent SonoVue under biological microscope

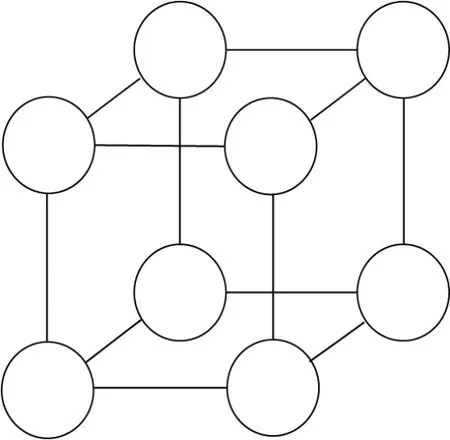
图2　微泡分布的正立方体结构模型Fig.2　Cube structure model of microbubble distribution

正立方体结构模型描述的是在中心处的一个红细胞(平均半径为3.6µm)受边角位置微泡温度的影响.因为微泡释放热量的过程较短,且热量向周围传递的距离也较近,所以较远处的微泡对中心处的温度影响可以忽略.因此,本工作中的计算只考虑正立方体8个边角对中心位置的温度影响.

1.2密排面心立方体结构模型

在医学实践中,靶向基因治疗(或高聚集超声热疗法等)往往在人体局部组织形成大量微泡的堆积,因此需要考虑多个微泡对同一区域的温度影响.当微泡浓度较高时,微泡分布密集,微泡之间的距离较近,可能发生黏连.

图3为六氟化硫微泡经过超声换能器(扫频式超声波换能器HNE-FP-SS1)照射30 s后微泡分布的形态,可以看出,部分微泡黏附在一起.由于微泡黏附在一起时的形状不确定,为了减少计算的复杂性,以密排面心立方体的结构建模(见图4).另外,假设这种构型的一个微泡团附着在机体组织的表面上,进而考察黏附表面的温度.

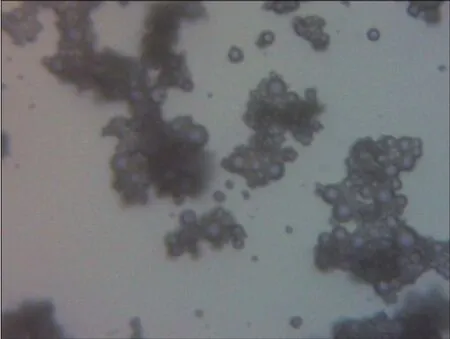
图3　超声换能器照射后黏连的微泡团Fig.3　Microbubbles attached to each other after ultrasonic transducer irradiation

2　计算过程和结果

对于单个微泡在超声激励下的能量计算,本工作选用Church[6]提出的有膜壳R-P方程建立模型,该模型描述了微泡在液体中振动时自身半径与外部声压随时间变化的关系.

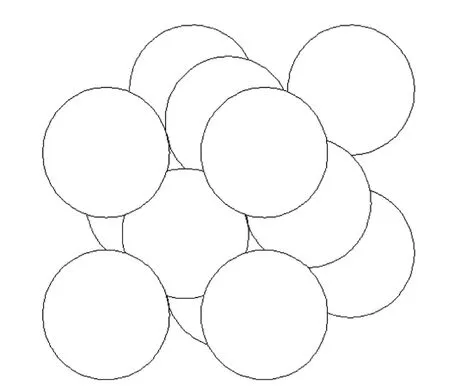
图4　微泡分布的密排面心立方体结构模型Fig.4　Closely-packed cube structure model of microbubble distribution

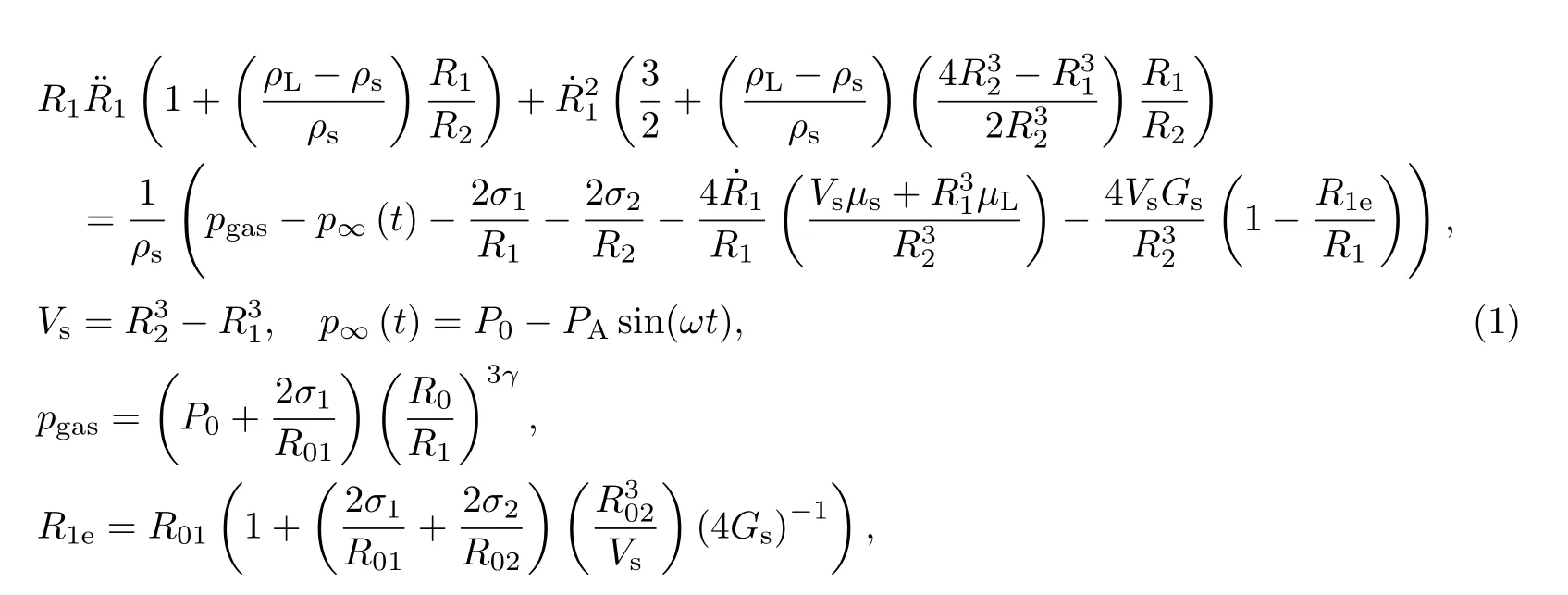
式中,R01,R02为微泡初始内外半径的值；R1,R2为振动开始后微泡的内外半径的值；其他相关参数及取值参见表1[13].

在一个超声脉冲周期内,微泡总能量的耗散为

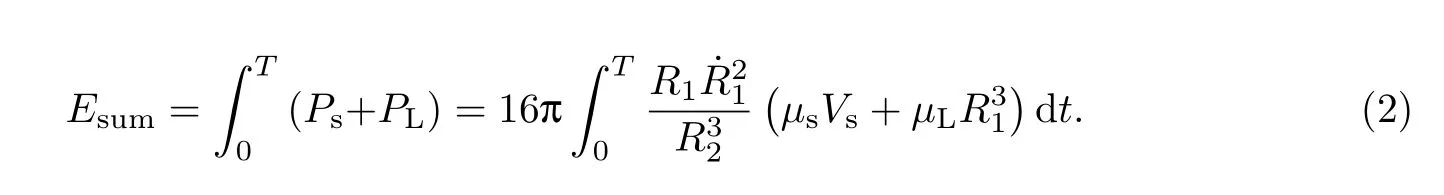
若将微泡视为一个球壳热源,在无限大介质中微泡瞬时放热后,任意时刻温度场的升温[14]为

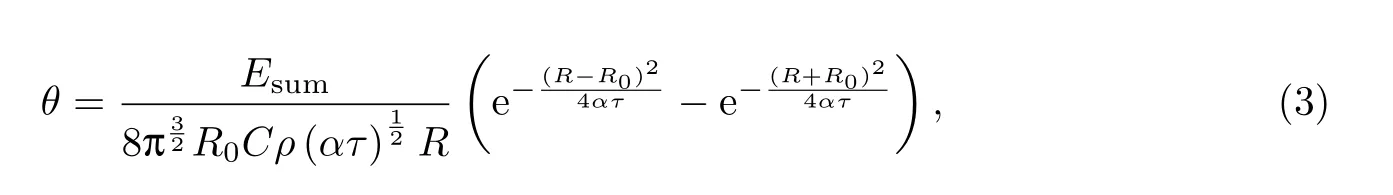
式中,τ为球壳热源瞬时放热后的时间,R为坐标原点到空间任意一点的距离,R0为球壳初始半径,其他参数均为介质参数(见表1).将由式(1)和(2)计算出的耗散能量值Esum作为初始能量,R0=3µm(即微泡半径距离)作为初始距离一并代入式(3),就可以得到经过一个超声脉冲周期后微泡释放能量的温度场.

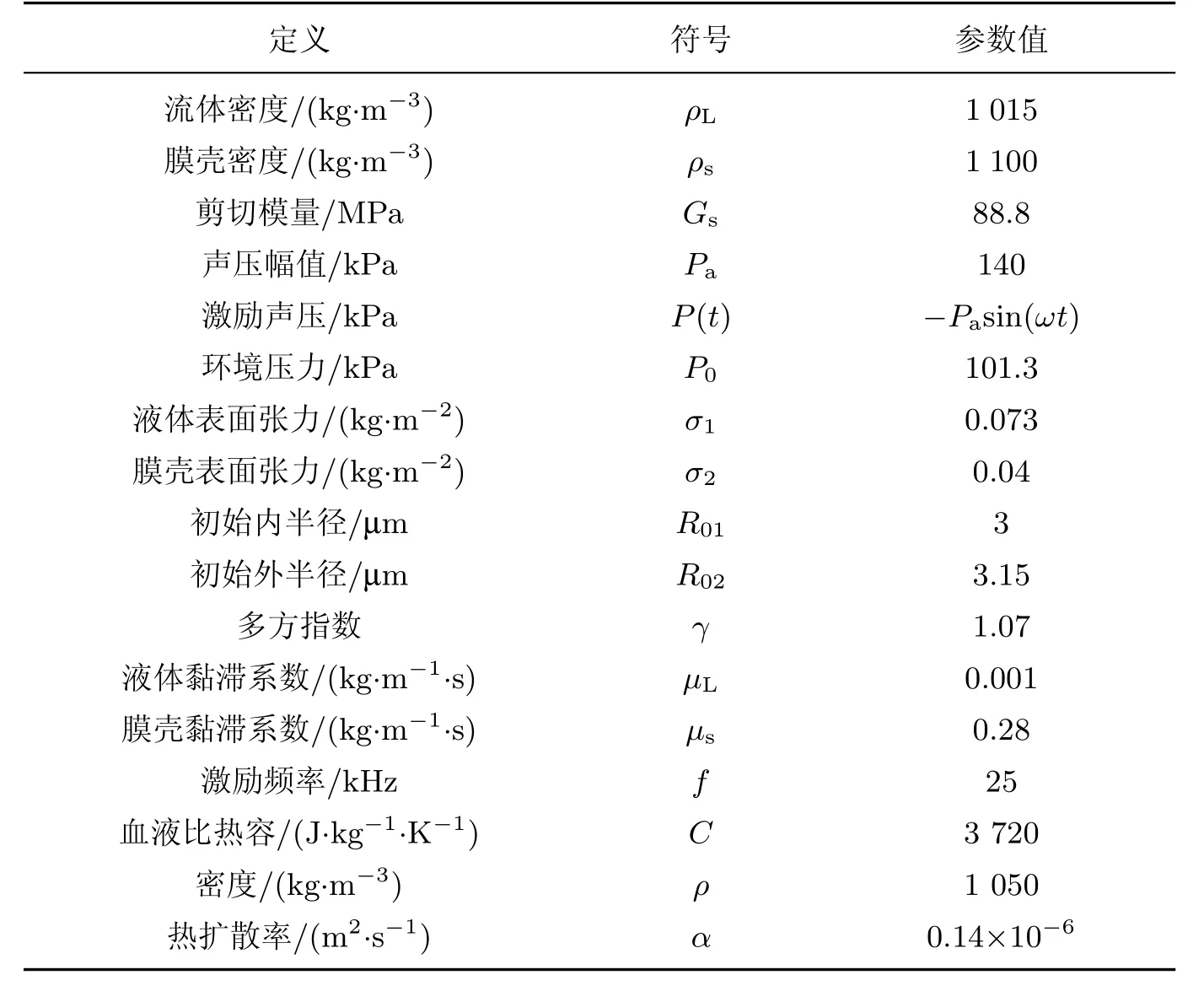
表1　R-P模型中参数的符号及取值Table 1　Notations and values of parameters for R-P model

下面计算血液环境下正立方体结构模型中微泡对中心红细胞的温度影响.图5为血液环境下微泡经历一个超声脉冲周期的温度场.可以看出,在靠近微泡表面的位置,温度最高上升至1.8°C,而随着传播距离的增加,温度呈现明显下降的趋势.因此,在构建模型时顶点微泡与中心红细胞之间的距离是影响温度变化的主要因素.假设正立方体模型8个顶点处的微泡形状完全相同,振动过程中释放的能量与温度也相同.由于多个微泡的温度场相互独立,温度场可以叠加,可以计算得到顶点微泡随距离增加而引起的中心红细胞温度的增量.

图5　血液环境下微泡经历一个超声脉冲周期的温度场Fig.5　Temperature field of microbubbles in the blood during an ultrasonic pulse period

图6为微泡和红细胞之间的距离与中心温度增量的关系.可以看出,当顶点微泡与中心点相距R=6µm(一个微泡直径)时,中心温度提高0.74°C,而当R≈9µm时,温度增量几乎为0,因此可以认为在距离超出9µm之后,顶点微泡产生的热量将不再影响中心温度.

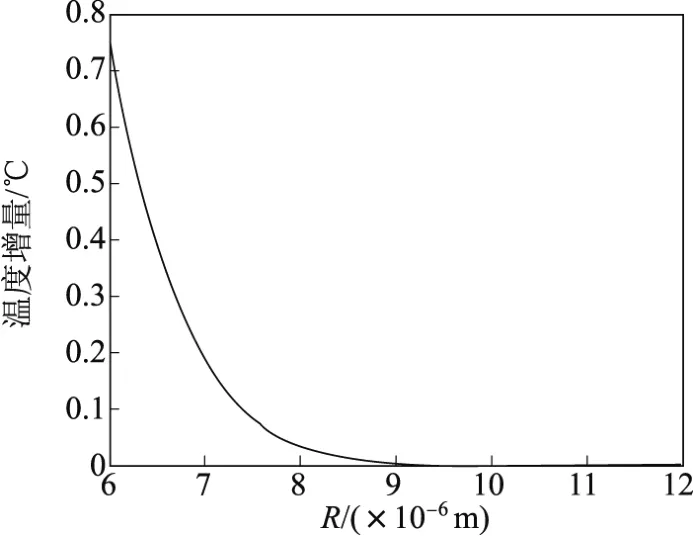
图6　微泡和红细胞的距离与中心温度增量的关系Fig.6　Relation between distance of microbubble to red blood cell and temperature rise in the center

接下来计算以密排面心立方体结构模型中微泡团对组织表面产生影响的温度场.图7为密排面心立方体投影下的矩形区域.

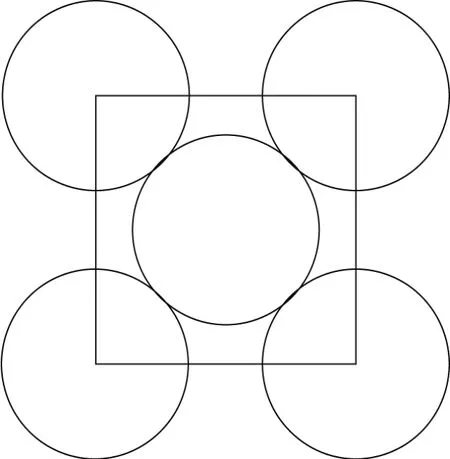
图7　密排面心立方体投影区域Fig.7　Projection region of the closely-packed cube

对于以密排面心立方体为结构的微泡团，与其黏连的矩形面积受到温度改变的影响最大.因此,以矩形中心点为坐标原点建立坐标系,对式(3)进行直角坐标变换,可得

然后将14个微泡空间坐标依次代入式(4),这样就可以计算出一个超声脉冲周期内微泡团产生的温度场,结果如图8所示.

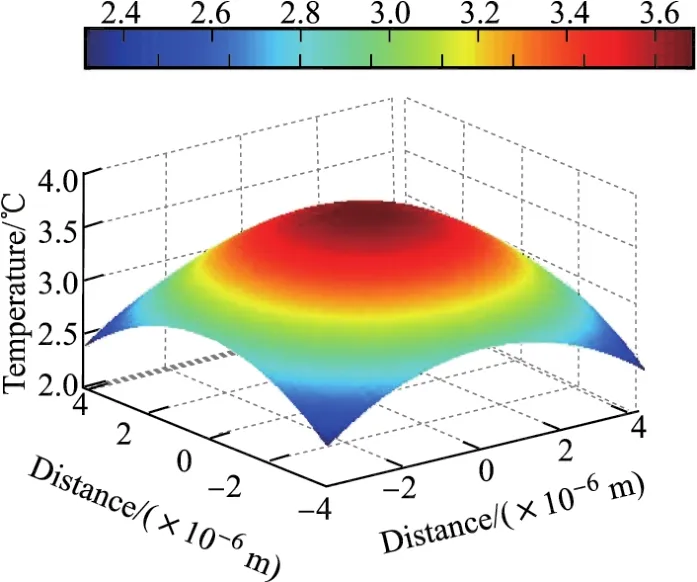
图8　密排面心立方体结构中组织表面矩形区域内的温度场Fig.8　Temperature field of organization surface in a rectangular region for closely-packed cube structure

由图8可以看出：矩形区域内的组织表面由于受到密排面心立方体微泡团所产生的温度影响,中心点处温度升高了3.72°C；由于结构的对称性,矩形曲面4个角处温度最低,均为2.36°C,且等高线上每一点的温度相同.根据医学有关规定,人体体温如果持续比正常体温高4°C,将会对组织器官产生伤害.由上述模型计算出的温度属于安全范畴之内,且真实情况下的微泡排布不会这么密集,同时人体血液流动等客观因素使温度不会恒定保持在这个数值上,所以上述计算结果符合安全标准.

3　结束语

本工作通过黏性耗散产生的能量,计算得到了磷脂薄膜超声造影剂在外界声压激励下,单个微泡在血液环境中的温度场.结合实验观测结果,发现微泡在液体环境下并不是以个体形式出现,因此提出了以一个红细胞为中心,8个微泡为顶点的正立方体模型.在此基础上通过计算微泡产生的热量对中心点处温度的影响,得出微泡与中心点处距离超过9µm后顶点微泡的温度将不再影响中心点温度的结论.另外,对于微泡浓度较高或出现微泡团黏滞在组织机体表面上的情况提出了密排面心立方体模型,通过计算该模型中微泡团对矩形区域产生的温度场,对其安全性进行了分析.

[1]HyNyNEN K.The threshold for thermally significant cavitation in dog’s thigh muscle in vivo[J]. Ultrasound in Medicine&Biology,1991,17(2)：157-169.

[2]ARyAL M,PARK J,VyKHODTSEvA N.Enhancement in blood-tumor barrier permeability and delivery of liposomal doxorubicin using focused ultrasound and microbubbles：evaluation during tumor progression in a rat gliomamodel[J].Physics in Medicine and Biology,2015,60(6)：2511-2527.

[3]IBSEN S,SHI G,ScHUTT C,et al.The behavior of lipid debris left on cell surfaces from microbubble based ultrasound molecular imaging[J].Ultrasonics,2014,54(8)：2090-2098.

[4]RAyLEIGH J W S.On the pressure developed in a liquid during the collapse of spherical cavity[J]. Philosophical Magazine,1917,34：94-98.

[5]PLESSET M S.The dynamics of cavitation bubbles[J].ASME Journal of Applied Mechanics, 1949,16(3)：277-282.

[6]CHURcH C C.The effects of an elastic solid surface layer on the radial pulsations of gas bubbles[J].The Journal of the Acoustical Society of America,1995,97(3)：1510-1521.

[7]ALLEN J S,MAy D J,FERRARA K W.Dynamics of therapeutic ultrasound contrast agents[J]. Ultrasound in Medicine&Biology,2002,28(6)：805-816.

[8]SONG J,ZHAO Z Q,WANG J G.Evaluation of contrast enhancement by carbon nanotubes for microwave-induced thermoacoustic tomography[J].IEEE Transactions on Biomedical Engineering,2015,62(3)：930-938.

[9]ABBOTTJG.RationaleandderivationofMIandTI—areview[J].Ultrasound in Medicine&Biology,1999,25(3)：431-441.

[10]ZHANG J M,LI C,ZHANG X,et al.In vivo tumor-targeted dual-modal fluorescence/CT imaging using a nanoprobe co-loaded with an aggregation-induced emission dye and gold nanoparticles[J].Biomaterials,2015,42：103-111.

[11]STRIDE E,SAFFARI N.On the destruction of microbubble ultrasound contrast agents[J]. Ultrasound in Medicine&Biology,2003,29(4)：563-573.

[12]STRIDE E,SAFFARI N.The potential for thermal damage posed by microbubble ultrasound contrast agents[J].Ultrasonics,2004,42：907-913.

[13]CARSLAw H S,JAEGER J C.Conduction of heat in solids[M].2nd ed.Cambridge：Oxford University Press,1959.

本文彩色版可登陆本刊网站查询：http://www.journal.shu.edu.cn

Temperature field of microbubble ultrasonic contrast agent in cube and closely-packed cube configurations

YANG Qing1,XU Kaiyu1,2,FENG Jiangtao1,2
(1.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China；
2.College of Sciences,Shanghai University,Shanghai 200444,China)

This paper studies the temperature field in blood by calculating viscous energy dissipation of phospholipid membrane based ultrasonic contrast agent under the sound pressure excitation.According to the experimental observation,a cube model with a red blood cell as center and eight microbubbles as vertices is proposed.Temperature rise of the center is also calculated.Furthermore,considering the condition of high microbubble concentration and its adhesion to the surface of organizations,a cube model of closelypacked structure is also built.Temperature field in a rectangular region and the peak temperature is obtained though this model.Safety is analyzed in detail to demonstrate feasibility and effectiveness of the proposed model.

ultrasonic contrast agent；dissipated energy；temperature field；cube model；closely-packed cube model

O 424

A

1007-2861(2016)05-0616-08

10.3969/j.issn.1007-2861.2015.02.014

2015-04-12

国家杰出青年科学基金资助项目(11102105)；上海市自然科学基金资助项目(15ZR1416100)

徐凯宇(1956—),男,教授,博士生导师,博士,研究方向为微纳米力学、生物材料力学. E-mail:kyxu@shu.edu.cn