求解非线性互补问题的一类光滑牛顿算法
孙菊贺,纪东辰,王 琪
(沈阳航空航天大学 理学院,沈阳 110136)
求解非线性互补问题的一类光滑牛顿算法
孙菊贺,纪东辰,王 琪
(沈阳航空航天大学 理学院,沈阳 110136)
主要研究一类光滑函数法求解非线性互补问题。基于Fischer-Burmeister(FB)互补函数的光滑形式,将非线性互补问题转化为一类光滑的非线性方程组问题。为了求解该光滑非线性方程组问题,提出一类的全局收敛光滑牛顿算法。讨论了方程算子的雅克比矩阵的非奇异性。应用所提出的牛顿方法求解一类互补问题,得到相应的数值结果。
非线性互补问题;互补函数;光滑牛顿法;非光滑性;收敛性
非线性互补问题(NCP)是指:求矢量x∈Rn,使其满足
x≥0,F(x)≥0,xTF(x)=0
(1)
其中F:Rn→Rn是连续可微的。
变分不等式和非线性互补问题(NCP)起源于20世纪60年代。到20世纪80年代变分不等式和非线性互补问题在数学规划领域中已经发展到一个卓有成效的学科,并将其应用到了工程学、经济学、物理学等重要领域中。
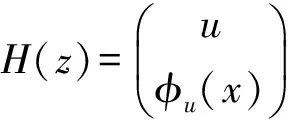
1 预备知识
定义 1.1 设φ:R2→R为二元函数且满足
φ(a,b)=0⟺a≥0,b≥0,ab=0
(2)
则二元函数φ称为非线性互补(NCP)函数。
所谓的FB函数是指
φFB(a,b)=(a2+b2)1/2-(a+b)
(3)
易得FB函数(3)是一类NCP函数且在原点处是不可微的。因此我们给出下面的光滑的FB函数
(4)
显然,当u>0时,φu(a,b)是连续可微的。
下面欲将非线性互补问题(1)转化为方程问题。先给出以下假设。
假设1.1 函数A:R→R连续可微,并且设A(u)满足以下3个条件:
(1)A′(u)>0对所有u∈R成立;
(2)A(u)有唯一零点u=0;
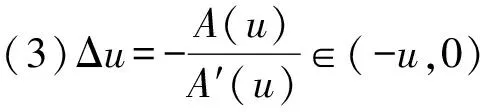
令
(5)
定义效益函数ψu;Rn→R+:
(6)
应用光滑函数(4)可以将(1)转化成下面非线性方程组问题:
(7)
其中z=(u,x)∈Rn+1,A:R→R满足假设1.1。令
(8)
则(1)等价于下面最小值问题:
(9)
注1.1 假设1.1对于下一部分的算法起着关键性的作用。根据假设1.1中的(1)可以得出H(u,x)的半光滑性;根据假设1.1中的(2)可以得出H(u,x)=0必然u=0;根据假设1.1中的(3)可以得出Δu<0,并且对t∈[0,1],u+tΔu>0,这意味着在下一部分的算法中迭代点列{uk}是递减的并且对于全部的k,uk>0。
下面的性质将在下一部分算法的收敛性证明中用到。
证明 很明显Γ(x)在(0,a)上连续可微,并且有
(10)
所以,Γ(x)在(0,a)上严格递增。
性质1.2 对于u1,u2≥0,x∈Rn,映射Φu满足以下不等式
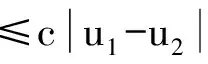
(11)
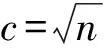
性质1.3 H(u,x)在u>0时连续可微,其Jacobin矩阵有如下形式:
(12)
其中C∈Rn,D和E都是Rn×n中的对角矩阵,并且满足
(13)
并且
(14)
2 光滑牛顿算法及其全局收敛性
我们提出了一类牛顿算法求解非线性方程组H(z)=0。这种算法包含牛顿步和梯度步,在没有F是单调的或是P0的条件下,该算法也是有效的。另外,在牛顿方程是不可解的时候,我们采用最速下降方向,这不同于经典的Armijo线搜索。
算法2.1

步骤2 (牛顿步)求解线性方程组
JH′(zk)Δz=-H(zk)
(15)
得到解Δzk∈Rn+1。设mk是{0,1,2,…,lmax}中满足下式的最小非负整数:
f(zk+λmkΔzk)≤(1-2σλmk)f(zk)
(16)
计算tk=λmk,zk+1=zk+tkΔzk,βk+1=βk.令k←k+1,转到步骤1。
Δxk=-Ψ(xk)
(17)
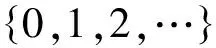
Ψ(xk+λmkΔxk)≤Ψ(xk)-σλmk‖Δxk‖2
(18)
令tk=λmk,xk+1=xk+tkΔxk,转步骤4;
步骤4 如果下式成立
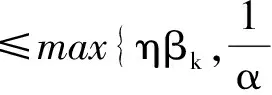
(19)
则令βk+1=‖Φ(xk+1)‖,并取uk+1:
(20)
如果(19)式不成立,那么令βk+1=βk,并取uk+1:
(21)
令zk+1=(uk+1,xk+1),k←k+1,转步骤1。
注2.1

(2)如果牛顿方程JH(zk)Δz=-H(zk)有解,设为Δzk,那么
即Δzk是效益函数f(z)在zk处的一个下降方向。
(3)如果线性方程组(15)无解或{0,1,2,…,lmax}中不存在mk满足(16)式,本部分最速下降方向负梯度-Ψ(x)为搜索方向,并采用经典的Armijo线搜索(18)进行搜索。此时,uk是一个光滑因子,uk+1的选取方法分成了(20)和(21)两种情况。
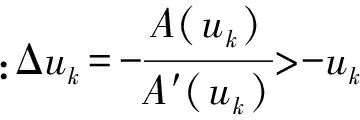
接下来,取A(u)=eu+u-1,给出下面的性质和定理。
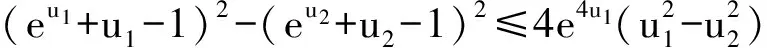
(2)首先,利用数学归纳法容易证明如下结论:对x≥y≥0,m为正整数,有
xm-ym≤(x-y)(x+y)m-1,又有
(eu1+u1-1)2-(eu2+u2-1)2=(eu1+eu2+u1+u2-2)(eu1+u1-eu2-u2)
(22)
其中
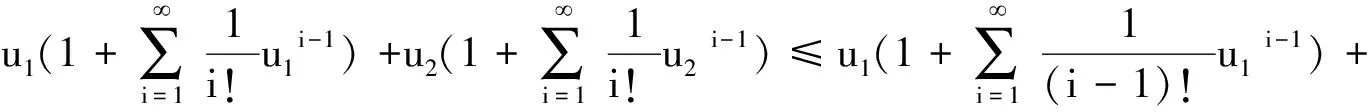
类似可以得到 (eu1+u1-eu2-u2)≤2e2u1(u1-u2)。完成证明。

注2.2 为了后续工作的方便,在性质2.1中取4u1。
定理2.1 对任何k≥0,如果zk=(uk,xk)∈R++×Rn并且步骤1的终止准则不成立,那么由算法产生序列zk+1=(uk+1,xk+1)∈R++×Rn。
证明 根据算法说明4易知uk+1>0,即(uk+1,xk+1)∈R++×Rn。
引理2.1 如果第k步采用牛顿步,那么uk+1≤(1-λlmaxe-u0)uk。
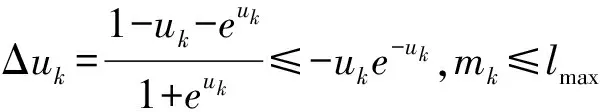
uk+λmk(-uke-uk)=uk(1-λmke-uk)≤uk(1-λlmaxe-u0)
结合式(20)和式(21),我们得到有以下结论。
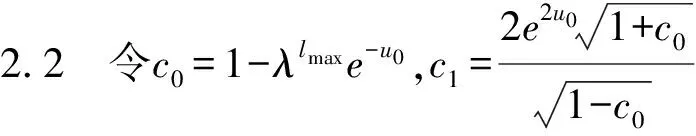
‖Φuk+1(xk+1)‖+c1uk+1≤‖Φuk(xk)‖+c1uk。 证明 由引理2.1可知,uk+1≤c0uk,再由性质1.1
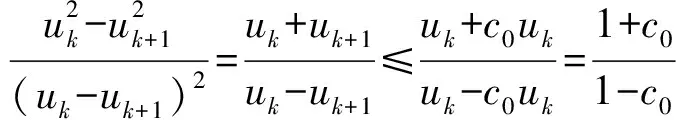
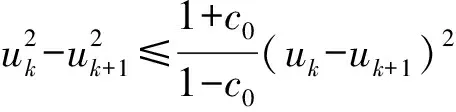
另一方面,由式(16),我们有
‖Φuk+1(xk+1)‖2+(euk+1+uk+1-1)2≤‖Φuk(xk)‖2+(euk+uk-1)2
并且

进而
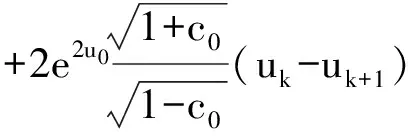
所以有
‖Φuk+1(xk+1)‖+c1uk+1≤‖Φuk(xk)‖+c1uk。
完成证明。
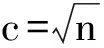
证明 根据式(18),有‖Φ(xk+1)‖<‖Φ(xk)‖,即‖Φ(xk)‖-‖Φ(xk+1)‖>0。由性质1.2,推出
‖Φuk+1(xk+1)‖≤‖Φuk+1(xk+1)-Φ(xk+1)‖+‖Φ(xk+1)‖≤cuk+1+‖Φ(xk+1)‖=
cuk+1+‖Φ(xk)‖-(‖Φ(xk)‖-‖Φ(xk+1)‖)≤
cuk+1+‖Φuk+1(xk)‖+(‖Φ(xk)‖-‖Φuk+1(xk)‖)-(‖Φ(xk)‖-‖Φ(xk+1)‖)≤
2cuk+1+‖Φuk+1(xk)‖-(‖Φ(xk)‖-‖Φ(xk+1)‖)
根据(21)得‖Φ(xk)‖-‖Φ(xk+1)‖≥2cuk+1,于是有‖Φuk+1(xk+1)‖≤‖Φuk+1(xk)‖且
‖Φuk+1(xk)‖≤‖Φuk(xk)‖+‖Φuk+1(xk)-Φuk(xk)‖≤‖Φuk(xk)‖+c(uk-uk+1)
即是‖Φuk+1(xk)‖+cuk+1≤‖Φuk(xk)‖+cuk。因此
‖Φuk+1(xk+1)‖+cuk+1≤‖Φuk+1(xk+1)‖+cuk+1≤‖Φuk(xk)‖+cuk
完成证明。
推论2.2 对k≥0,如果(19)不成立,那么

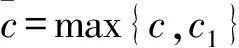
我们给出两个标集:
L={k∈N|第k-1步采用了梯度步}
引理2.4 假设集合K由0=k0 从(1)到(2),对kj∈K,总有βkj≤rβkj-1,j=1,2,…,进而βkj≤rjβ0=rj‖Φ(x0)‖。 完成证明。 证明 任意给定k∈N,记kj为集合K中满足kj 首先证明下面的不等式成立: (23) 分两种情况:(1)如果kj=k,则‖Φ(xk)‖=‖Φ(xkj)‖=βkj,(23)式显然成立。 (2)如果kj≠k,即kj 结合性质1.2,有 由引理2.4, 即xk∈L0。完成证明。 推论2.3 设算法2.1产生的点列为{zk=(uk,xk)},那么任给k,有 证明 对k∈N,uk≤u0,那么我们有 引理2.5 设算法2.1产生的点列为{zk=(uk,xk)},假设下标集K为无限集,则点列{xk}的任一极限点都是NCP问题的一个解。 引理2.6 设算法2.1产生的点列为{zk=(uk,xk)},{xk}L1是其子序列且以x*∈Rn为极限点,如果∀k∈L1,第k次迭代采用梯度步,那么x*是Ψ的一个稳定点。 并且 下面用反证法来证明x*是Ψ(x)的稳定点。若不然,则Ψ(x*)≠0。首先证明。假如,由于对k∈L1,Δxk=-Ψ(xk)由(17)式可知 故 所以 Ψ(xk+λmk-1Δxk)≤Ψ(xk)-σλmk-1‖Δxk‖2,即 而对k∈L1,Δxk=-Ψ(xk),故 即(1-σ)‖Ψ(x*)‖2≤0。由假设Ψ(x*)≠0,那么σ≥1,这与算法2.1中σ∈(0,1)矛盾。所以只能有Ψ(x*)=0即x*是Ψ(x)的稳定点。完成证明。 由以上结论不难得到下面的全局收敛定理。 定理2.3 设算法2.1产生的点列为{zk=(uk,xk)},则 (1){uk}线性收敛到0; (2){xk}的任一极限点都是函数Ψ(x)的稳定点。 在本部分中,参数选取: lmax=16,λ=0.5,σ=0.001,α=0.1,η=0.8 当效益函数Ψ(x)≤ε或迭代次数超过500时终止。以下算例可以在文献[6-7]中找到。 例子3.1 使 表1 例子3.1的数值结果 初始点牛顿步次数梯度步次数解Ψ(X)(0,0,0)1021(2000001,1342840,0764282)866e-11(01,01,01)791(2000013,1342842,0764282)902e-11(1,1,1)681(200000,1342840,0764282)915e-11(2,1,1)221(200000,1342843,0764282)771e-11(2,13,07)170(200000,1342843,0764280)905e-11(2,2,2)290(200000,1342843,0764282)815e-11(10,10,10)1151(2000013,1342840,0764282)988e-11(-1,-1,-1)741(2000012,1342840,0764282)930e-11 通过算例的结果可以看出,本部分构造的光滑牛顿法具有较好的全局收敛性,在任何点处都能在有限步内收敛到互补问题的解,并且在解的附近具有较快的收敛速率,这也从实际上说明了算法的收敛性质。 本文利用光滑的FB函数将互补问题转化为光滑方程组问题,并提出一类光滑牛顿算法求解该光滑方程组问题。本文的两点在于:(1) 光滑方程组中用函数A(u)替代了常规的u,并给出A(u)的一类特殊的选取方式,令 A(u)=eu+u-1; (2)算法的设计中包含牛顿步和梯度步两种,这样不仅降低了计算的复杂度使算法具有全局收敛性,也加大了该算法的使用范围。最后的一个经典算例说明了该算法的有效性。 [1]AGHASSI M,BERTSIMAS D,PERAKIS.Soving asymmetric variational inequalities via convex optimization[J].Operations Research Letters,2006,34(5):481-490. [2]CHEN X D,SUN D,SUN J.Complementarity functions and numerical experiments on some smoothing Newton methods for second-order-cone complementarity problems[J].Computational Optimization and Applications,2003,25(1-3):39-56. [3]FACCHINIEI F,PANG J S.Finite-dimensional variational inequalities and complementarity problems,Volume II[M].New York:Springer-Verlag,2003. [4]FUKUSHIMA M.Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems[J].Mathematical Programming,1992,53(1):99-110. [5]SUN J H,WANG L.A smoothing Newton method based on the generalized Fischer-Burmeister function for variational inequality problem[J].Journal of Convergence Information Technology,2013,8(1):151-160. [6]PANG J S,GABRIEL S A.NE/SQP:A robust algorithm for the nonlinear complementarity problem[J].Mathematical Programming,1993,60(3):295-337. [7]MANGASARIAN D L,SOLODOV M V.Nonlinear complementarity as unconstrained and constrained minimization[J].Mathematical Programming,1993,62(1):277-297. [8]SUN D,SUN J.Strong semismoothness of the Fischer-Burmeister SDC and SOC complementarity functions.Mathematical Programming,2005,103(3):575-581. [9]PAN S,CHEN J.A semismooth Newton method for the SOCCP based on a one-parametric class of SOC complementarity functions[J].Computational Optimization and Applications,2010,45(1):59-88. [10]PAN S,KUM S,LIM Y,et al.On the generalized Fischer-Burmeister merit function for the second-order cone complementarity problem[J].Mathematics of Computation,2014,83(83):1143-1171. [11]HAO Z,WAN Z,CHI X,et al.A power penalty method for second-order cone nonlinear complementarity problems[J].Operations Research Letters,2015,290(2):136-149. [12]SUN J H,ZHANG L W.A globally convergent method based on Fischer-Burmeister operators for solving second-order-cone constrained variational inequality problems[J].Computers and Mathematics with Applications,2009,58(10):1936-1946. [13]SUN J H,CHEN J S,KO C H.Neural networks for solving second-order cone constrained variational inequality problem[J].Computational Optimization and Applications,2012,51(2):623-648. [14]QI L,SUN D,ZHOU G.A new look at smoothing Newton method for nonlinear complementarity problems and box constrained variational inequalities[J].Mathematical Programming,2000,87(1):1-35. [15]FUKUSHIMA M,LUO Z Q,TSENG P.Smoothing functions for second-order-cone complementarity problem[J].SIAM Journal on Optimization,2002,12(2):436-460. (责任编辑:吴萍 英文审校:刘勇进) A Class of smoothing newton methods for solving nonlinear complementarity problem SUN Ju-he,JI Dong-chen,WANG Qi (College of Science,Shenyang Aerospace University,Shenyang 110136,China) We study a class of smoothing function methods for solving nonlinear complementarity problem in this paper.Based on the well-known Fischer-Burmeister function,we transform the nonlinear complementarity problem into a system of nonlinear smooth equations.For solving the system of nonlinear smooth equations,we construct a class of smoothing Newton methods and prove its global convergence,while discussing the nonsingularity of Jacobian matrix of the equation operator.An illustrative example is given to show the performance of the smoothing Newton method. nonlinear complementarity problem;complementary function;smoothing Newton method;non-smooth;convergence 2016-01-21 国家自然科学基金(项目编号:11301348) 孙菊贺(1980-),女,辽宁沈阳人,副教授,主要研究方向:变分分析理论与优化算法,E-mail:juhesun@163.com。 2095-1248(2016)05-0074-08 O221.2 A 10.3969/j.issn.2095-1248.2016.05.014 基础科学与工程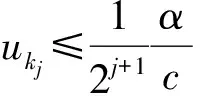
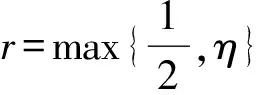
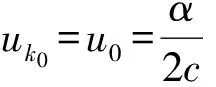
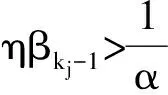
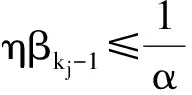
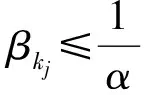
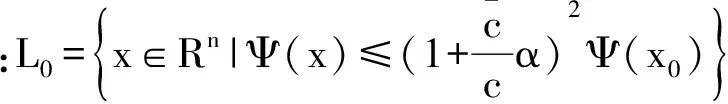
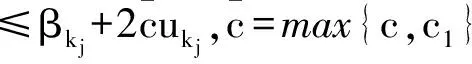
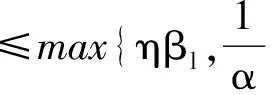

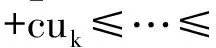


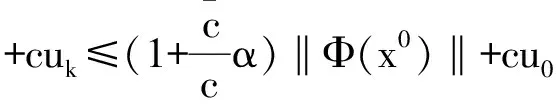
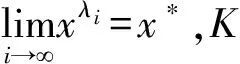
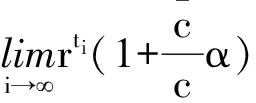
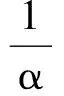




3 数值试验

4 总结

