基于梯度投影取样的改进Kriging方法

赵维涛，唐 恺，祁武超

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136)



基于梯度投影取样的改进Kriging方法

赵维涛，唐 恺，祁武超

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136)

在结构可靠性分析过程中，Kriging方法是工程实际中常用方法之一。但样本点选取对Kriging模型预测精度具有一定影响，样本点过多计算效率低下，样本点过少难以保证预测精度。基于结构可靠性分析特点，充分利用梯度投影技术的优势，结合样本点筛选技术，合理选取用于构建Kriging模型的样本点。数值算例表明，方法求得的设计点、可靠性指标和失效概率均具有满意的计算精度，且方法所需样本点数量明显少于其它方法，计算效率较高。

结构可靠性；Kriging模型；梯度投影；样本筛选

在实际工程中，对于某些大型复杂结构，输入变量和输出变量之间往往具有较高的非线性关系，很难得到输入变量和输出变量之间的明确表达式，这给结构可靠性分析带来一定的困难。虽然Monte Carlo Simulation(MSC)可以解决此类问题并能够得到较精准的解，但该方法需要调用有限元次数过多，计算效率低下。针对上述问题，国内外学者提出了很多改进方法，例如Response Surface Method(RSM)[1-2]和Kriging[3-5]方法等。RSM通常使用一个简单的函数代替设计点附近的极限状态函数，但RSM的计算精度对响应函数形式和样本点选取具有较大的敏感性[6-8]。Kriging方法相对而言比较灵活，在解决具有高度非线性极限状态函数的可靠性分析问题时，亦能取得良好的拟合效果。Kaymaz[5]指出在结构可靠性分析过程中，如果Kriging模型建立适当，其结果要优于经典RSM。张崎和李兴斯[9]使用全局网格型和拉丁超立方抽样对结构进行了基于Kriging模型的可靠性分析，这种全局模型可以将所有样本点的响应值都模拟出来，相当于得到了极限状态函数的显式表达式。刘瞻等[10]提出了基于重要抽样的Kriging方法，并将该方法用于结构的可靠性分析之中。

Kriging模型是由一个参数模型和一个非参数随机过程组成的半参数模型，已有研究[11-14]表明“样本点的选择对Kriging模型预测精度具有一定的影响，样本点过多计算效率低下，样本点过少难以保证预测精度”。Gomes等[15]指出在结构可靠度计算时，梯度投影技术是最优的样本点选取方法之一。本文将结合结构可靠性分析的特点，充分利用梯度投影技术的优势，合理选取用于构建Kriging模型的样本点，在保证计算精度的前提下，提高结构可靠性分析的计算效率。

1 经典Kriging方法简介

已知有m个n维样本点[X1,X2,…,Xm]及其响应值Y={y1,y2,…,m}T，其中Xi={xi1,xi2,…,xin}T，i=1,2,…,m。Kriging模型[11-12]如式(1)所示。

(1)

式中：F为回归函数矩阵，β为回归系数，ε为随机误差，下标p为回归函数的项数。

回归函数提供模拟的全局近似，即响应值的期望。在经典Kriging模型中，常用的回归函数为多项式函数。通常情况下，回归函数的形式对拟合精度不起决定性的作用。当回归函数取为线性多项式时有p=n+1，此时回归函数矩阵F的任意一行，如式(2)所示。

(2)

随机误差提供模拟局部偏差的近似，即响应值的局部变化。在经典Kriging模型中，假定随机误差ε1,ε2,…,εm均服从正态分布且相互不独立[13]，即如式(3)和(4)所示。

(3)

(4)

式中：σε为随机误差的标准差，R(θ,Xi,Xj)为样本点Xi和Xj之间的相关系数，θ={θ1,θ2,…,θn}T为模型参数。

在经典Kriging模型中，相关系数一般选为高斯模型[14]，即如式(5)所示。

R(θ,Xi,Xj)=exp[-θ1(xi1-xj1)2-θ2(xi2-xj2)2-…-θn(xin-xjn)2]

(5)

在经典Kriging模型中，式(1)中的回归系数可以利用广义最小二乘法得到，如式(6)所示。

β*=(FTR-1F)-1FTR-1Y

(6)

式中：R是随机误差的相关系数矩阵，具体形式如式(7)所示。

(7)

(8)

模型参数θ可通过如下的非线性无约束优化问题求得，具体公式如式(9)所示。

(9)

(10)

式中：r(X*)是预测点X*与样本点之间的相关系数向量，即如式(11)所示。

r(X*)={R(θ,X1,X*),R(θ,X2,X*),…,R(θ,Xm,X*)}T

(11)

根据式(10)可求得Kriging模型对预测点X*偏导数，如式(12)所示。

(12)

式中：Jf(X*)和Jr(X*)分别是f(X*)和r(X*)的雅可比矩阵。

2 改进Kriging方法

2.1 基本流程

本文方法的总体思路如下：首先利用少量样本点构建初始Kriging模型，并利用初始Kriging模型采用FORM(First Order Reliability Method)求解设计点；然后在设计点附近区域利用梯度投影技术增加新的样本点，并对新增样本点进行筛选；最后将筛选后的样本点增加到之前样本点集合中，进而更新Kriging模型以提高Kriging模型在设计点附近的预测精度。本文方法的基本流程如图1，具体步骤如下:

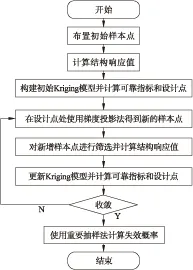
图1 计算流程图

(1) 以均值点为中心，按照Bucher提出的实验设计[1]确定初始样本点，并计算样本点对应的结构响应值；

(2)构建初始Kriging模型，其中回归模型根据样本点数量选择线性或二次多项式模型，相关系数模型选取高斯模型；

(3)基于初始Kriging模型，使用FORM求解结构可靠指标β及设计点XD；

(4)在XD处利用梯度投影法增加2n+1个样本点；

(5)对新增样本点进行筛选，然后将筛选后的样本点增加到先前样本点集合中，并更新已有Kriging模型；

(6)根据更新后的Kriging模型，使用FORM求解可靠指标β及设计点XD；

(7)重复步骤4到步骤6，直至满足收敛准则(收敛准则为相邻两次迭代的可靠性指标相对变化小于0.1%)；

(8)根据最终的Kriging模型，利用重要抽样法计算结构失效概率Pf。

2.2 样本点选取

设计点XD={xD1,xD2,…,xDn}T，则设计点XD中第j个分量xDj投影用到的向量Tj及单位向量tj分别如式(13)和(14)所示。

Tj=ej-(αTej)α, j=1,2,...,n

(13)

(14)

式中：ej为第j坐标轴方向的单位基向量，α为极限状态函数G(X)在XD处的单位负梯度向量，即如式(15)所示。

(15)

为了使新增样本点合理地位于真实极限状态面附近，用到单位投影向量qj，即如式(16)所示。

(16)

式中：γ为一小数(γ=10-3)，ω是加权因子，0≤ω≤1，本文采用全向量投影即ω=1。 根据上式，新增样本点Sj坐标如式(17)所示。

(17)

j=1,2,…,n

(18)

式中：σj是第j个随机变量的标准差，参数k为取样步长，文中k=1。

梯度投影法可以得到2n个样本点，加上设计点XD共新增样本点个数为2n+1个。令Xd=Sn+1，新增样本点与之前样本点总个数为m+2n+1，如式(19)所示。

[X1,X2,…,Xm,S1,S2,…,S2n+1]=

(19)

2.3 样本点筛选

若新增样本点与之前样本点之间距离过小，一方面会造成样本点的浪费，一方面可能会产生病态的回归函数矩阵。因此为提高计算效率和模型预测精度，本文采用如下方法对新增样本点进行筛选。

首先将新增样本点与之前样本点均转换到标准正态空间内，如式(20)和(21)所示。

(20)

(21)

式中：Ui和Hj为标准正态空间内的样本点，μ和σ分别为随机变量的均值矢量和标准差矢量。

然后计算任意新增样本点Hj与之前所有样本点在标准正态空间内的距离，并判断该距离是否过小，具体公式如式(22)所示。

‖Ui-Hj‖≤γ i=1,2,…,m，j=1,2,…,2n+1

(22)

式中：γ为一小数(γ=10-3)

若Hj满足式(22)，则认为样本点Sj与之前样本点之间的距离过小，进而将样本点Sj删除；若不满足，则保留样本点Sj。

3 算例

3.1 算例1

已知结构极限状态函数，如式(23)所示：

G(X)=x1x2-1500

(23)

式中：x1和x2均服从正态分布，均值为μ={38，54}T，标准差为σ={3.8,2.7}T。

在标准正态空间内(U空间)，应用本文方法所布置的样本点如图2。从图2中可以看出，本文方法所布置的样本点能够较好地落在设计点和极限状态曲面附近，能够提高Kriging模型在设计点附近的预测精度。

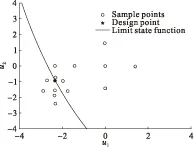
图2 本文方法的样本点

数值计算结果见表1。表1中xD1和xD2为设计点坐标，NFE代表极限状态函数的评估次数(即样本点个数)。从表1中可以看出，对比设计点坐标、可靠性指标和失效概率，本文方法均具有较好的计算精度；对比NFE(即样本点个数)，本文方法所需样本点数量明显少于其它方法，本文方法具有较高的计算效率。

表1 数值计算结果(算例1)

方法xD1xD2βNFEPf/10-3MCS---10663经典RSM[10]2915350049239246583经典Kriging[10]2924751092247513667文献[10]2921451344247953665FORM29144514682512030-本文方法2914451468251201563

3.2 算例2

已知结构极限状态函数，如式(24)所示：

(24)

式中：x1至x4均服从正态分布，均值为μ={107,2.5×10-4,0.98,20}T，标准差为σ={106,2.5×10-5,0.098,8}T。

应用本文方法求得的数值计算结果见表2。从表2中可以看出，就设计点、可靠性指标和失效概率而言，本文方法均具有满意的计算精度。本文方法共迭代4次，样本点总数量9+9+2+1=21个。在第1次迭代过程中，本文方法共布置9个初始样本点，在后续每次迭代过程中均利用梯度投影法新增9个样本点并对新增样本点进行筛选，在第3次和第4次迭代过程中分别筛选掉7个样本点和8个样本点。由于本文采用了样本点的筛选技术，使得样本点数量进一步减少。对比NFE，本文方法具有较高的计算效率。

表2 数值计算结果(算例2)

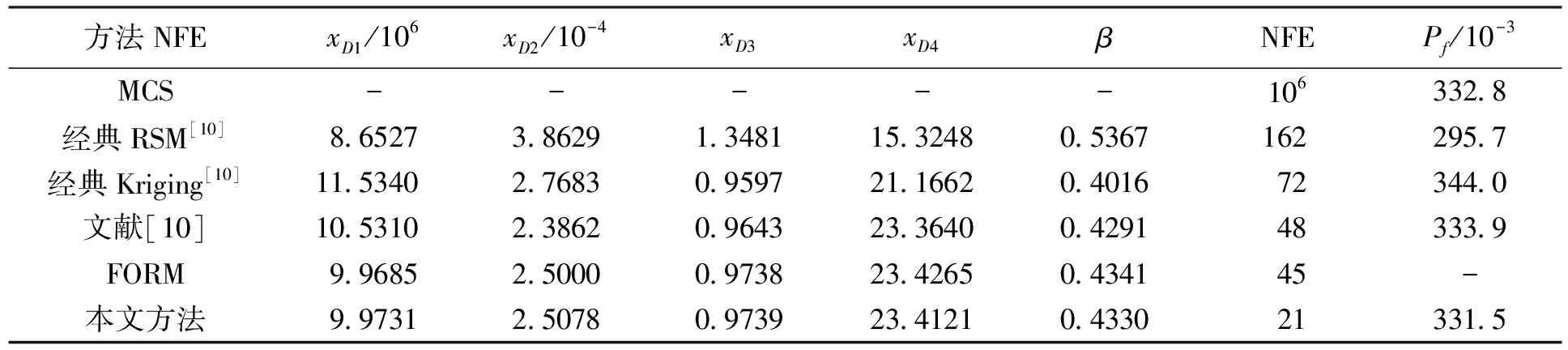
方法NFExD1/106xD2/10-4xD3xD4βNFEPf/10-3MCS-----1063328经典RSM[10]865273862913481153248053671622957经典Kriging[10]115340276830959721166204016723440文献[10]105310238620964323364004291483339FORM9968525000097382342650434145-本文方法99731250780973923412104330213315

4 结论

基于结构可靠性分析的特点，本文充分利用梯度投影技术的优势，合理选取用于构建Kriging模型的样本点，能够以少量样本点给出在设计点附近的极限状态函数信息。在迭代计算过程中，为了避免样本点的距离过近而导致的样本点浪费现象发生，本文对新增样本点进行筛选，进一步合理减少样本点数量。

数值算例分析表明，本文方法求得的设计点、可靠性指标和失效概率均具有满意的计算精度；相对极限状态函数的评估次数(即样本点个数)，本文方法所需样本点明显少于其它方法，计算效率较高。

[1]BUCHER C G,BOURGUND U.A fast and efficient response surface approach for structural reliability problems[J].Structural Safety,1990,7(1):57-66.

[2]KIM S H,NA S W.Response surface method using vector projected sampling points[J].Structural Safety,1997,19(1):3-19.

[3]ANTHONY A G,WATSON L T.A comparison of approximation modeling techniques:polynomial versus interpolating models[R].AIAA 98-4758,St.Louis,USA,September ,1998.

[4]TIMOTHY W S.Comparison of response surface and kriging models in the multidisciplinary design of an aerospike nozzle[R].NASA/CR-1998-206935,Hampton,USA,February,1998.

[5]KAYMAZ I.Application of Kriging method to structural reliability problems[J].Structural Safety,2005,27(2):133-151.

[6]WEITAO Z,XUEYAN S,KAI T.A response surface method based on sub-region of interest for structural reliability analysis[J].Structural Engineering and Mechanics,2016,57(4):587-602.

[7]赵维涛,邱志平.基于合理子域的改进响应面方法[J].力学学报,2014,46(3):409-416.

[8]赵维涛,邱志平.基于切平面布点的一种改进响应面方法[J].工程力学,2014,31(10):21-26.

[9]张崎,李兴斯.基于Kriging模型的结构可靠性分析[J].计算力学学报,2006,23(2):175-179.

[10]刘瞻,张建国,王灿灿,等.基于优化Kriging模型和重要抽样法的结构可靠度混合算法[J].航空学报,2013,34(6):1347-1355.

[11]SOREN N L,NIELSEN H B,SONDERGAARD J.Aspects of the matlab toolbox DACE[R].IMM-REP-2002-13,Technical University of Denmark,Lyngby,Denmark,2002.

[12]SOREN N L,NIELSEN H B.A matlab Kriging toolbox[R].IMM-TR-2002-12,Technical University of Denmark,Lyngby,Denmark,2002.

[13]RASMUSSEN C E,WILLIAMS CKI.Gaussian processes for machine learning[M].MIT Press,Massachusetts,USA,2006.

[14]AU S K,BECK J L.Estimation of small failure probabilities in high dimensions by subset simulation[J].Probabilistic Engineering Mechanics,2001,16(4):263-277.

[15]GOMES H M,AWRUCH A M.Comparison of response surface and neural network with other methods for structural reliability analysis[J].Structural Safety,2004,26(1):49-67.

(责任编辑：刘划 英文审校：赵欢)

Improved Kriging method based on gradient projection sampling

ZHAO Wei-tao,TANG Kai,QI Wu-chao

(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation, Shenyang Aerospace University,Shenyang 110136,China)

Kriging method is one of the common methods for analyzing structural reliability in engineering practice.However,the selection of samples has a great influence on the accuracy of Kriging model.A large number of samples can lead to low efficiency,and few samples can not ensure the accuracy of prediction.In this paper,an improved Kriging method was proposed based on the characteristics of structural reliability analysis,the gradient projection technique and the sample screening technique.The method selected appropriate amount of samples to construct the Kriging model.The numerical results indicate that the improved method can obtain approving accuracy for the calculation of design point,reliability index and failure probability.The number of samples selected by the improved method is remarkably less than that by other methods and the calculation efficiency is higher.

structural reliability;Kriging model;gradient projection;sample selecting

2016-05-06

国家自然科学基金(项目编号：11502149)；辽宁省自然科学基金(项目编号：201602579)；航空科学基金(项目编号：2013ZA54004)；辽宁省教育厅(项目编号：L2014072) 。

赵维涛(1977-)，男，辽宁沈阳人，副教授，主要研究方向：飞机结构强度与可靠性，E-mail:zhwt201@126.com。

航空宇航工程

2095-1248(2016)05-0001-05

V215.7

A

10.3969/j.issn.2095-1248.2016.05.001