一种面向计数问题的公式发现方法

蔡东风,朱耀辉,白 宇

(沈阳航空航天大学 知识工程研究中心，沈阳 110136)



一种面向计数问题的公式发现方法

蔡东风,朱耀辉,白 宇

(沈阳航空航天大学 知识工程研究中心，沈阳 110136)

在分析计数问题特点的基础之上，提出了一种面向计数问题的公式发现方法。该方法能根据给定的计数数列，自动发现其计数递推公式。将计数递推公式按公式的系数不同分为10种不同的公式类型(也称公式模式)，对给定的计数数列，采用SVM方法进行公式模式的分类，采用求解线性方程组方法对识别的公式模式参数进行求解，并为了防止过拟合得到错误的公式，利用专用的验证数据对求解后得到的具体计数递推公式进行公式验证。最后，采用国际公开的整数数列集OEIS中的645个计数问题进行十折交叉验证实验，求解正确率达92.56%。在新公式发现实验中，发现了目前OEIS数据集中尚未包含的10个新公式。

公式发现；机器发现；计数问题；模式分类；递推公式

由于人工求解计数问题，特别是对比较复杂的计数问题相当困难，本文尝试利用机器学习的方法自动发现计数公式，提出了一种利用SVM进行公式模式的分类和利用线性方程组对公式模式的参数进行求解的计数公式发现方法，简称基于模式(模式分类+模式求解)的公式发现方法。

迄今为止，已有多种公式发现[1]方法被提出。其中，Pat Langly等人1977年提出的BACON系统[2-4]是公式发现的先驱,成功地重新发现了开普勒行星运动第三定律、理想气体定律、万有引力定律等物理和化学公式。Zembowitz[5]等人在搜索公式时考虑数据的误差进而研发了FAHRENHEI系统。Dzeroski[6-7]等人采用多元线性回归同时考虑多个变量，并添加微分项拓展公式发现的范围。随后，公式发现系统被用于科学模型的修正[8-9]，针对特定领域公式发现[10-11]。此外，国内陈文伟[12-15]等人基于原型函数库，利用启发式搜索不断寻找具有最佳线性逼近关系的原型函数，并结合曲线拟合技术来求得数据间的规律。

以上发现系统在面向物理、化学方面的公式发现上表现出较好的效果,但是在面向计数问题的公式发现上存在困难。这主要是因为计数公式与物理、化学公式存在明显的不同。首先，计数公式的数据是整数，而物理、化学公式的数据是实数，一般求解同样的整数域问题要比实数域困难；其次，用于学习计数公式的数据要求是精准无噪声的，而用于学习物理、化学公式的经验数据可能含有误差或噪声，要求学到的计数公式必须精准地满足所有已给数据；最后，计数公式的数据通常在整数域内无限延伸，而物理、化学公式的数据通常在一个相对固定的实数域内变化。这些差别说明对于计数公式的发现需要采用新的方法。

因此，本文在分析计数问题和计数公式的特点基础之上，提出了一种新的计数公式发现方法，能自动地发现计数递推公式。按公式的系数不同分为10种不同的公式类型(也称公式模式)，采用“模式分类+模式求解”的方法进行公式发现。最后，在国际公开的整数数列集OEIS(On-Line Encyclopedia of Integer Sequence)上进行发现实验，求解正确率达92.56%，并发现了一些目前OEIS数据集中没有的新公式。

1 计数问题及计数公式

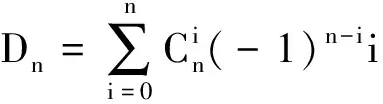
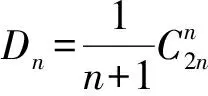
从以上实例可见，无论是复杂的求和、还是含有组合数以及阶乘等常见的计数公式表达，往往可以化为递推公式形式。在实际计数问题中，复杂的通式公式若能转化为递推表达，通常会比较简单且易于理解[16-17]。例如，著名的“斐波那契数列”的通式表示包含无理数，而递推公式却非常简单(Dn=Dn-1+Dn-2)。递推公式作为公式，特别是计数公式的一种表示形式，具有非常强的表达能力，有些复杂的递推表达很难找到或根本不存在非递推表达。因此，本研究采用计数公式的递推表示形式。

2 基于模式的计数公式发现方法

提出一种基于模式的计数公式发现方法。该方法能根据给定的计数数列，自动地发现其计数递推公式。将递推公式分为不同模式，采用SVM[18]方法进行公式模式的分类，采用求解线性方程组方法对识别的公式模式的参数进行求解，并为了防止过拟合得到错误的公式，利用预留的验证数据对求解后得到的具体计数递推公式进行公式验证。

2.1 公式模式

递推公式也称差分方程，其一般形式如公式(1)所示，称为k阶递推公式。h为递推函数，ui表示当n=i时的计数值，称为递推变量或差分变量，un和un-k分别称为首项和尾项；f(n)为齐次项，当f(n)=0时，称为齐次递推公式；当f(n)≠0时，称为非齐次递推公式。

h(un,un-1,…,un-k,n)=f(n)(n≥k≥1)

(1)

本文分析了OEIS中大量已知计数问题的计数公式，发现绝大多数情况下，递推函数h都是递推变量ui的线性组合，即式(2)的形式。其中gi(n)是n的多项式函数，一般为常数或n的3阶以下的多项式，g0(n)的次数越低且gi(n)(i>0)的次数越高表示计数数列增长越快。

(2)

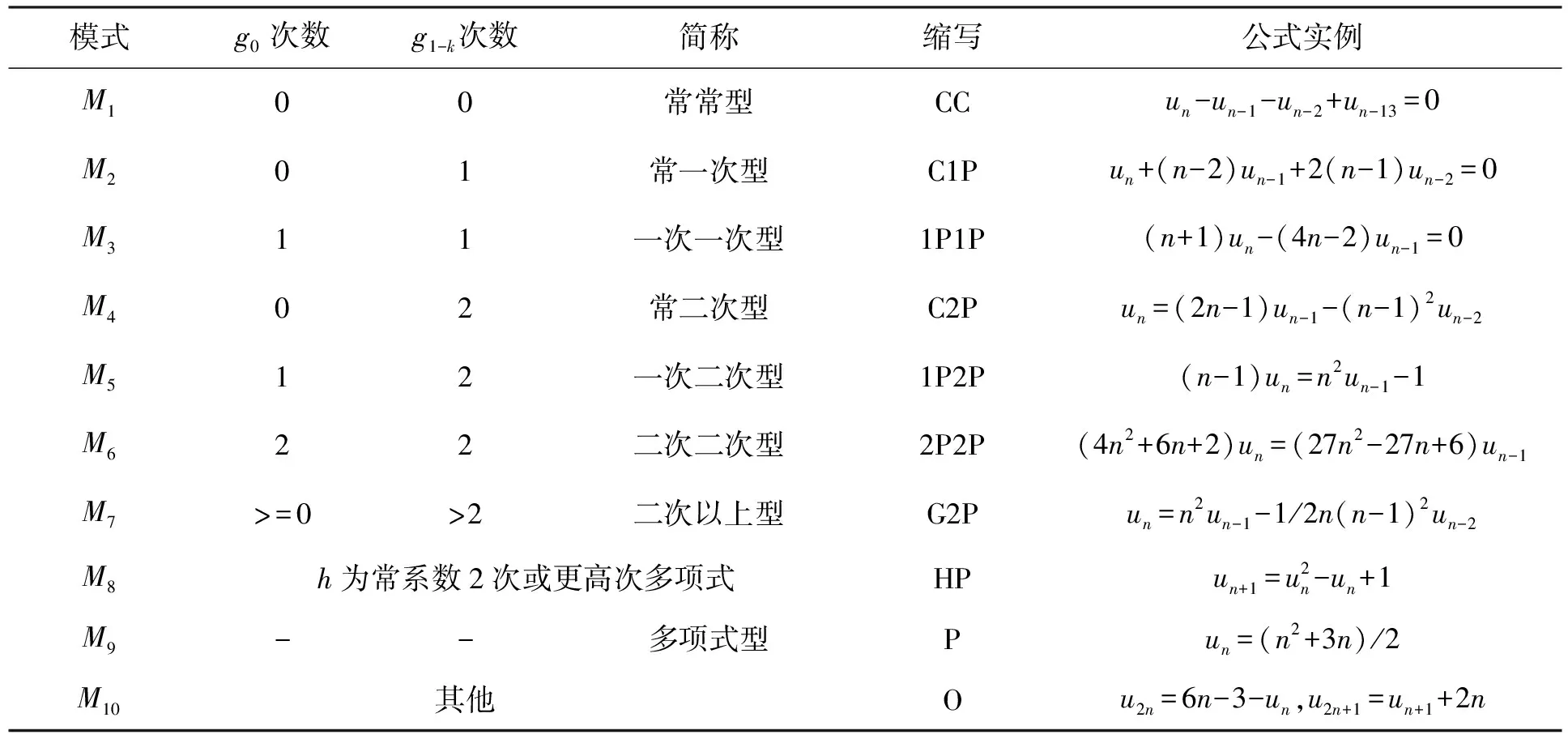
因此，按递推公式的首项系数g0(n)以及其它变量系数gi(n)，将式(2)分为如表1所示的7种公式模式(M1-M7)，再加入最常见的多项式模式(M9)，齐次项为多项式型和递推函数h为常系数2次或更高次多项式模式(M8)以及其他模式(M10)，总共分为10种公式模型。另外，式(2)中齐次项函数f(n)也可分为以下4种类型，其中多项式类型最为常见。

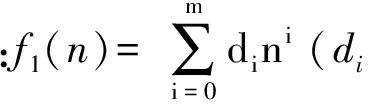
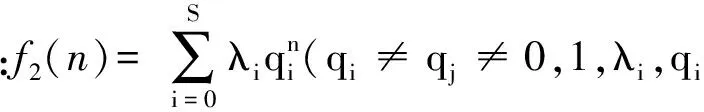
(P+E型)：f3(n)=f1(n)+f2(n)

表1 递推公式模式(g0-k的次数为0表示常数，- 表示不存在)

模式g0次数g1-k次数简称缩写公式实例M100常常型CCun-un-1-un-2+un-13=0M201常一次型C1Pun+(n-2)un-1+2(n-1)un-2=0M311一次一次型1P1P(n+1)un-(4n-2)un-1=0M402常二次型C2Pun=(2n-1)un-1-(n-1)2un-2M512一次二次型1P2P(n-1)un=n2un-1-1M622二次二次型2P2P(4n2+6n+2)un=(27n2-27n+6)un-1M7>=0>2二次以上型G2Pun=n2un-1-1/2n(n-1)2un-2M8h为常系数2次或更高次多项式HPun+1=u2n-un+1M9--多项式型Pun=(n2+3n)/2M10其他Ou2n=6n-3-un，u2n+1=un+1+2n

2.2 基于模式的公式发现方法

图1是本文提出的基于模式的计数公式发现方法或系统的流程图。该系统由数列输入、特征抽取、模式分类、模式求解、公式验证、公式输出以及模式库等组成。在模式库中，记录每种模式的ID、类型、模式描述、模式求解方法等。算法流程如下：

(1) 模型训练。利用已给数据训练不同模式的SVM模型。由于是多模式分类问题，采用分类精度相对高的OVO方法；

(2) 实例输入。输入计数问题的计数数列I的前m个计数值，记为Im。并将其前m1个作为学习数据Ie和后m2=m-m1个作为验证数据It；

(3) 特征抽取。对Ie进行特征抽取和缩放处理，生成输入实例的特征向量Vi；

(4) 模式分类。利用SVM模型，对Vi进行公式模式的分类，保留前nbest分类结果到nbest模式列表中；

(5) nbest控制。如果nbest模式列表为空，则失败停止，否则从列表中取出当前最好模式m；

(6) 模式求解。利用模式库和学习数据Ie，对模式进行求解，即确定模式的具体参数。如求解成功，表示发现了满足Ie的公式F，否则转(5)；

(7) 公式验证。验证F是否满足验证数据It。如果成功，输出公式F，停止，否则转(5)。

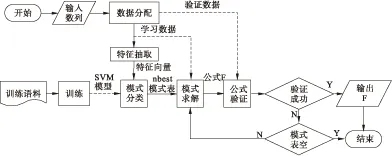
图1 公式发现系统流程图

本方法的最终目标是发现计数公式，不是公式模式的分类。不同于一般分类问题，SVM模式分类的主要作用是可将更有希望的模式放在前面求解，可显著提高系统的效率。对于无法求解的计数数列，给出的分类模式也可以作为研究人员的参考。下面对模式分类(包括特征抽取)、模式求解以及公式验证进行具体介绍。

2.2.1 模式分类

模式分类的关键是根据问题和样本的特点选择合适的特征。针对计数问题，输入样本是计数数列，记为U=u1,u2,…，un,其主要特点是随n的增大通项un趋向正无穷大，数值的变化范围很大，没有固定范围，数据间关系密切不独立。结合分类模式的特点，本文在分类特征的选择上着重对数列的变化趋势进行度量，并假设变化趋势相似的数列其对应的公式模式相同。通过实验，最后确定了如下定义的增长量和增长率两类特征。

增长量(I)：相邻数据项的差分，Inci=ui+1-ui

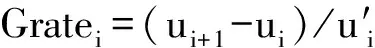
例如：给定数列U=1，3，8，15，24，35，48，……。取前n=7个数据作为学习数据进行特征化处理。对应的1阶特征数列为：

增长量数列I=2，5，7，9，11，13

增长率数列R=2，5/3，7/8，9/15，11/24，13/35

对于生成的不同特征数列，还可以进一步特征化处理，生成高阶特征数列。如对应上述增长量数列I，可再进行特征化处理，称为2阶特征数列(II，IR)。

I的增长量数列 II=3，2，2，2，2

I的增长量数列 IR=3/2，2/5，2/7，2/9，2/11

一般高阶特征能提供更深层的信息，但相对低阶特征，获取高阶特征需要的数据更多且计算量更大。通常特征化处理后的特征值的变化范围还很大，不适合直接用于模式分类，本文在模式分类前采用反正切函数将其映射在(-π/2，π/2)之间，即对某一特征值x，映射后的值为y=atan(x)，其中atan为反正切函数。

计数问题要求计数公式必须能完全精确匹配给定的数据(包括学习数据和验证数据)，即使这样，学习到的计数公式也不一定是正确的，有可能出现过拟合现象，这是归纳学习的特点和无奈。但是，相对学习到的计数公式的参数个数，给定数据比较多时，学习效果一般会比较好。另外，计数数列一定是非负整数数列，通常是递增非负整数数列，随着n的增大通项将趋向正无穷大，这点对机器学习的特征选择影响较大。

基于以上特征抽取和映射，采用SVM[19]方法进行公式模式分类。SVM在多分类问题上，常用的方法有“一对余(One-VS-Rest)OVR”和“一对一(One-VS-One)OVO”方法，OVR需要二分类器的个数少，但是分类结果通常比OVO差，所以本文采用OVO方法。

另外，由于一个数列的递推表示有时可能对应多种模式，即数列与公式模式是多对多的关系。因此，算法中采用nbest的求解方式，如果仅在nbest模式列表为空时停止，可发现更多的公式模式或新的公式。

2.2.2 模式求解

模式求解是指给定输入的计数数列和分类的公式模式的条件下，确定模式参数的过程，即发现满足已给学习数据的计数公式。不同模式可以采用不同的方法求解，一般可转化为代数方程组，特别是线性方程组求解。但是，许多计数问题的计数值很大，有时很难获得较多的输入数据。例如，n皇后问题的不同解的计数问题，当n=26时，解数为22 317 699 616 364 044,这是目前已知解数的最大n值。因此，公式模式中的参数个数不可设定过多，要依据输入数据的多少确定，有时需要对递推公式的阶数和递推函数系数的次数进行权衡和限制。另外，即使求解成功，得到候选公式，还需要进一步通过验证数据的验证才能作为输出，以防由于过拟合生成错误公式。

对于参数较多的高阶或高次的递推公式模式，往往由于可用数据的不足或没有好的求解方法，有些暂时还不能求解，如后面实验中G2P模式的实例。

2.2.3 公式验证

公式验证是指利用验证数据对由前面模式分类和模式求解得到的候选计数公式进行验证的过程，是防止由于数据过拟合造成发现错误公式的必要步骤。

验证数据是输入数据的一部分，但要独立于学习数据，即输入数据=学习数据+验证数据。实际应用中，可根据输入数据的多少确定学习数据和验证数据的比例分配，学习数据越多，可以学习到参数更多的复杂模型，而验证数据越多，会使我们对学习到并通过验证的公式的正确性更有信心。在本文实验中，采取了尽量增加学习数据和保证至少一个验证数据的原则，取得了很好的效果。但是，无论如何，自动公式发现是基于数据的归纳学习，通过有限的采样数据归纳学习得到的公式即使通过验证数据的验证，也不一定就能满足其它的新数据。因此，严格意义上说，自动发现的计数公式应该被认识是通过了有限数据验证的原计数问题计数公式的一个假说或一个还需要证明的定理。对于相关研究人员可能是一个很有意义的提示和辅助，或是一个一直期待的结果。

3 实验与分析

3.1 实验数据与算法设置

OEIS(On-Line Encyclopedia of Integer Sequences)是一个在线整数数列百科全书。它由Neil J. A. Sloane在1964年创建，截至到2011年11月已容纳超过二十万个数列，其解释涉及超过3千篇相关图书和文章。 OEIS对每一个数列都有详细表述，包括：数列的来源，数列的相关文献，已发现的数列公式，生成数列的程序，求解数列的难易程度等。整数数列包括由计数问题产生的计数数列，计数数列是整数数列的主要组成部分。OEIS是公认的研究计数问题的重要公开资源。

本实验包括已有公式的再发现实验(实验一)和新公式的发现实验(实验二)。实验一中的实验数据取自OEIS公开数据集标号为A000001～A003000中的递推公式和多项式公式，共计645个计数问题或计数数列；实验二将实验一的全部数据作为模型训练数据，对A000001～A000300的计数问题进行新公式的发现实验。

算法设置是指以下实验中的一些参数的确定。主要包括：SVM模型训练数据取为u6～u15，特征阶数为3，学习数据范围因问题而异，公式验证数据1个以上。以上设置都是通过实验选取的经验值。例如，计数数列开始时的数据一般并不能很好地显示出数据的变化趋势，通过实验选择训练数据从u6开始。

3.2 公式再发现实验

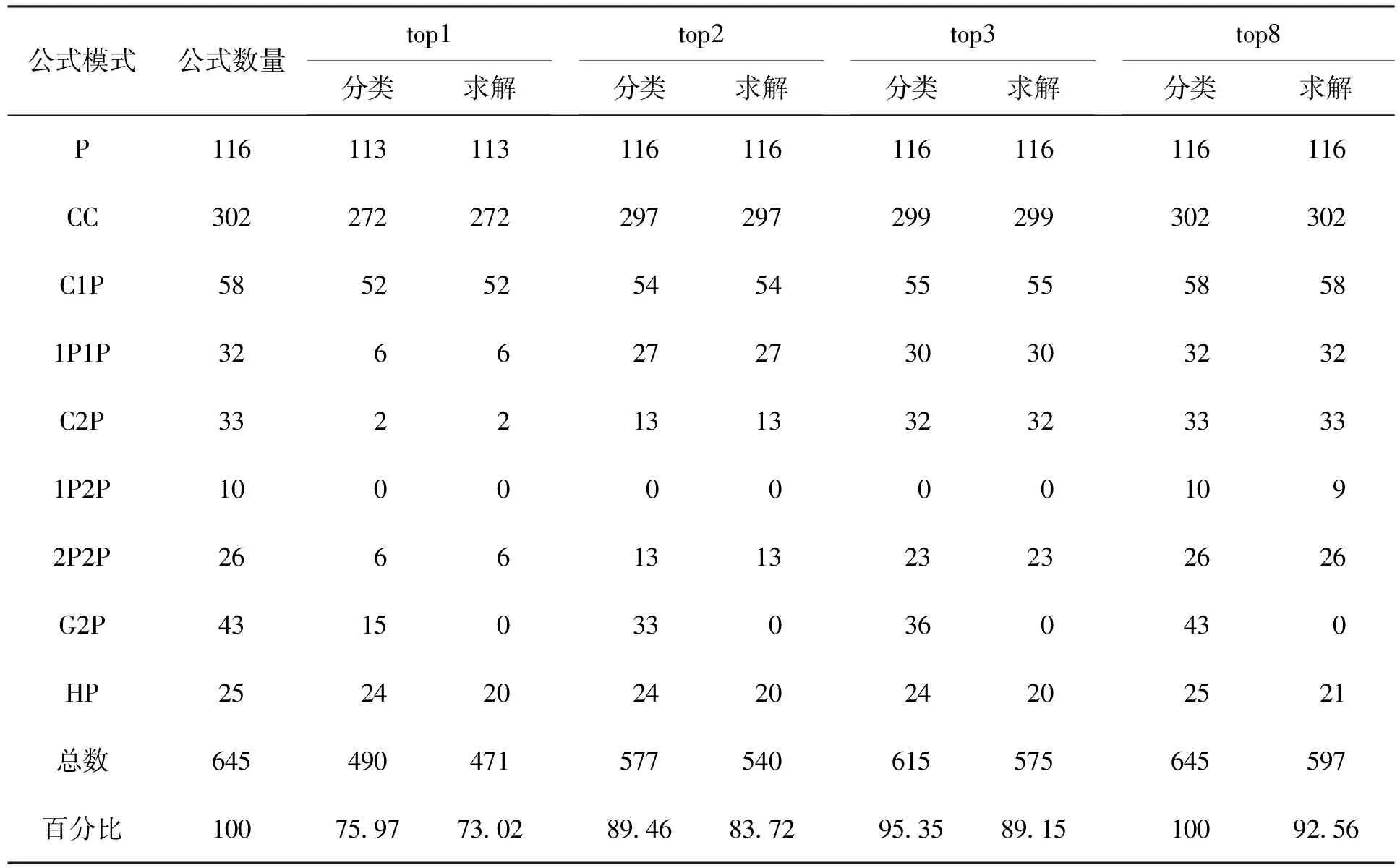
本实验采用2.2节提出的基于模式的计数公式发现方法，对上述OEIS实验数据集的645个问题进行十折交叉验证实验，实验结果如图2和表2所示。其中，“分类”表示能正确分类的公式模式，“求解”表示能正确求解的计数公式。图2和表2给出了在不同nbest取值的情况下，能够正确分类和求解的问题的比率曲线和具体数值。可见，top1-top3的模式分类正确率分别为：75.97%，89.46%，95.35%，已达到相当高的水平，而top8达到100%，平均每个模式分类仅需要循环1.42次。top1-top3的模式求解正确率分别为：73.02%、83.72%、89.15%，而top8达92.56%。总之，通过本实验验证了基于模式的递推公式发现方法是有效的，OEIS中的645个问题中，共求解597个，求解率达90%以上。

另外，表2进一步给出了按不同模式(共9类模式，不包括其它类)的分类和求解的具体问题个数及比率。可见，不同模式的公式分布非常不均匀，常系数递推公式模式(CC)和多项式公式模式(P)共记418个，占整个数据集的64.8%。P、CC、C1P、HP四类公式模式分类效果较好，而1P2P、2P2P模式的训练实例很少导致分类效果相对较差；HP模式的训练实例虽也不多，

但其分类与求解效果都较好，说明高次的特征明显；另外，对于参数较多的高次系数公式模式G2P，实验中由于可用数据相对较少，还需要寻找更有效的求解方法。

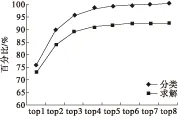
图2 模式分类和模式求解的nbest变化曲线

公式模式公式数量top1分类求解top2分类求解top3分类求解top8分类求解P116113113116116116116116116CC302272272297297299299302302C1P5852525454555558581P1P3266272730303232C2P33221313323233331P2P100000001092P2P2666131323232626G2P43150330360430HP252420242024202521总数645490471577540615575645597百分比1007597730289468372953589151009256

3.3 新公式发现实验

采用本文提出方法对OEIS集A000001～A000300共300个数列进行新公式发现实验，共发现新公式10个。发现的新公式如表3所示。表中“原公式”表示OEIS中已存在的公式，“新公式”表示本实验发现的新公式。“原公式”一栏仅列出与对应的“新公式”模式较相近的公式，并不是全部原公式。实验结果可知，A000115的原公式是非连续函数，但也能得到递推公式表达；A000202没有原公式，发现了较简洁的常系数递推公式；A000130和A000222也没有原公式，分别发现了较高次的递推公式；A000128、A000150、A000180、A000266、A000245、A000256存在原公式，但又发现了不同模式的新公式。

另外，为了保证发现公式的正确性，本文对以上发现的新公式使用OEIS提供的对应问题的全部数据进行了公式验证，结果全部顺利通过验证。

表3 新公式发现实验结果(序号上的数字表示n开始计数的数字)

OEIS问题序号原公式新发现公式A0001150un=[(n+4)2/20]un-un-2-un-5+un-7=1(n>6)]A0001281非递推un-un-1-un-2=12n2-52n+4(n>2)A0001300无(n-3)un-(n2-2n-3)un-1+(n2-4n+5)un-2+(n2-6n+5)un-3-(n2-3n+2)un-4=0(n>3)A0001500非递推(n2+n)un-(6n2-6n)un-1+(8n2-40n+36)un-2+(8n2+8n-72)un-3-(48n2-336n+576)un-4+(64n2-608n+1440)un-5=0(n>4)A0001842非递推(n-1)un=(12n-14)un-1-(48n-64)un-2+(64n-96)(un-3)(n>4)A0002021无un-un-1-nn-8+un-9=0(n>9)A0002220无un-(n-5/2)un-1-(5/2n-6)un-2-(3n-21/2)un-3-(5/2n-23/2)un-4-(n-9/2)un-5-un-6(n>5)A00024502P2P型(n+2)un=(5n+2)un-1-(4n-6)un-2(n>1)A0002563G2P型(n2-11/2n+15/2)un-(13/2n2-423/8n+845/8)un-1-(27/16n2-189/16n+165/8)(un-2=0)(n>5)A0002660非递推un=nun-1-(n-1)un-2+(n2-3n+2)un-3(n>2)

4 结论

本文首次提出了基于模式(模式分类+模式求解)的计数公式发现方法。在OEIS数据集上的实验结果表明，该方法能以较高的正确率再现已有公式，并能发现一些新的计数公式。需要强调的是，通过扩充更多的不同类型的公式模式，该方法能发现不限于递推公式形式的更为复杂多样的计数公式，也能用于其它问题类型的数学公式的发现或辅助发现。

[1]TODOROVSKI L.Equation Discovery[M].Springer US,2011.

[2]LANGLEY P,BRADSHAW G L,SIMON H A.BACON.5:The discovery of conservation laws[C]//IJCAI.1981,81:121-126.

[3]LANGLEY P,BRADSHAW G L,SIMON H A.Rediscovering chemistry with the BACON system[M]//Machine learning.Springer Berlin Heidelberg,1983:307-329.

[4]LANGLEY P,ZYTKOW J M.Data-driven approaches to empirical discovery[J].Artificial Intelligence,1989,40(1-3):283-312.

[5]ZEMBOWICZ R,YTKOW J M.Discovery of equations:experimental evaluation of convergence[C]//AAAI.San Jose,Ca,July.1992:70-75.

[6]DZEROSKI S,TODOROVSKI L.Discovering dynamics:from inductive logic programming to machine discovery[J].Journal of Intelligent Information Systems,1995,4(1):89-108.

[7]TODOROVSKI L,DZEROSKI S.Declarative bias in equation discovery[C]//ICML.1997:376-384.

[8]SAITO K,LANGLEY P,GRENAGER T,et al.Computational revision of quantitative scientific models[C]//International Conference on Discovery Science.Springer Berlin Heidelberg,2001:336-349.

[9]TODOROVSKI L,SAO D06EROSKI,LANGLEY P,et al.Using equation discovery to revise an earth ecosystem model of the carbon net production[J].Ecological Modelling,2003,170(170):141-154.

[10]TODOROVSKI L,DŽEROSKI S.Integrating domain knowledge in equation discovery[M]//Computational Discovery of Scientific Knowledge.Springer Berlin Heidelberg,2007:69-97.

[11]DŽEROSKI S，TODOROVSKI L.Equation discovery for systems biology:finding the structure and dynamics of biological networks from time course data.[J].Current Opinion in Biotechnology,2008,19(4):360-368.

[12]陈文伟,张帅.经验公式发现系统 FDD[J].小型微型计算机系统,1999,20(6):410-413.

[13]冯金花,陈燕雷,关永.经验公式发现系统(FDD)中对误差的改进[J].计算机工程与设计,2008,29(20):5287 -5289.

[14]陈燕雷,孟俊仙,关永.经验公式发现系统FDD函数库的扩充与改进[J].微计算机信息,2010,26(27):232-234.

[15]陈燕雷,孟俊仙,关永.经验公式发现FDD搜索方向判断标准的改进[J].微计算机信息,2011,27(4):238-239.

[16]韩林.巧用递推公式求解四类计数问题[J].数学教学通讯：教师阅读,2011(24):49-50.

[17]唐保祥,任韩.几类特殊图完美匹配数目的递推求法[J].西南师范大学学报：自然科学版,2014(2):9-13.

[18]CHANG C C,LIN C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology(TIST),2011,2(3):27.

[19]郎宇宁.基于支持向量机的多分类方法研究及应用[D].成都:西南交通大学,2010.

(责任编辑：刘划 英文审校：赵亮)

Formula discovery method for counting problem

CAI Dong-feng，ZHU Yao-hui， BAI Yu

(Knowledge Engineering Research Center,Shenyang Aerospace University,Shenyang 110136,China)

Inspired by the property of counting problems,we proposed a formula discovery method for counting problem.The method could automatically derive the recursion formula corresponding to some given counting sequence.Specifically,we first grouped the recursion formulas into different types,i.e.pattern,and then used SVM to do pattern classification on the input counting sequence.When the pattern was determined,we obtained the specific recursion formula by calculating the parameters(in the pattern),which could be translated into solving system of linear equations.Finally,we checked the correctness of the discovered recursion formula on unused part of the input data.By using the ten-fold cross validation test,we achieved 92.56% accuracy on 645 counting problems from the On-line Encyclopedia of Integer Sequence(OEIS).In the meanwhile,we discovered 10 new formulas are not included in OEIS.

formula discovery;machine discovery;counting problem;pattern classification;recursion formula

2015-10-28

蔡东风(1958-)，男，辽宁沈阳人，教授，主要研究方向：人工智能、自然语言处理，E-mail:caidf@vip.163.com。

2095-1248(2016)05-0061-07

TP391.1

A

10.3969/j.issn.2095-1248.2016.05.012