输液管道热膨胀状态下的超临界振动

李 阳，方 勃

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)



输液管道热膨胀状态下的超临界振动

李 阳，方 勃

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

应用工程实践中常用的Euler梁模型，研究在热膨胀作用下，随着液体流速的加快，输液管道的屈曲变形和固有频率的变化情况。通过Hamilton原理推导出输液管道的曲线平衡位形微分方程，并分析了热膨胀对输液管屈曲构型的影响。通过伽辽金(Galerkin)离散方法，得到了在热膨胀作用和液体流速达到超临界时，输液管道一阶固有频率的解析解。对比在液体流速达到超临界时,热膨胀对输液管道屈曲变形和一阶固有频率的影响。

超临界；热膨胀；非线性振动；频率

输液管道的振动在许多工程实践中都有广泛的应用，如航空宇航工程、核电工程、水利工程、石油工程等诸多工程领域[1-2]。早在1993年Paidoussis就对悬臂输液管道进行了非线性振动分析[3]，paidoussis和Semer在1994年分别用微元法和能量法建立了目前比较完善的非线性动力学模型[4]。倪樵和黄玉盈[5]在2001年利用谐波平衡法分析了非线性约束黏弹性输液管的动力学特性。上述研究中，通常假定液体是定常均匀流动的，而在实际工程应用中液体流速有时会随着时间的变化而改变，并且当输液管道的液体流速超过临界值时，就会引起管道的静力屈曲，即发生屈曲失稳[6-8]。荆红英、金基铎[9]等人在2009年计算了一端固定具有中间支承输液管道的临界流速问题，并分析了其稳定性。Holmes[10-11]采用中心流型定理研究了四维空间系统，指出平衡位形的不稳定属于屈曲失稳，并证明了支承输液管不会颤振。但在很多工程实践中，输液管道的工况不同同样会引起输液管道的振动，其中温度变化影响输液管道的振动是近几年被国内外学者广泛研究和讨论的，如太阳帆板内薄壁管结构在绕过地球阴影受到太阳辐射时的温度变化问题[12-14]，吴晓和张龙庭等人[15]以KBM法为基础，引进谐波平衡观点来对弹性直杆在热膨胀状态下进行非线性振动分析，Qian，Wang 和 Ni[16]在2009年对两端简支输液管道在热载荷作用下进行不稳定分析。

本文结合工程实际应用，在缪旭，金基铎[17]等人对输流管道的超临界固有频率问题分析的基础上，研究了在均匀温度场影响下，液体速度达到临界值时，输液管道的屈曲变形和固有频率的变化情况，并通过对比有无热膨胀影响来分析输液管的非线性振动特性。

1 运动微分方程

如图1，采用了工程实践中常用的Euler梁来建立两端简支的输液管道模型。其中主梁长度为L,单元长度管道的质量为m,抗弯刚度为EI，不可压缩流体单位质量为M,流体轴向流速为U，通流截面的面积为A,热管壁厚为h，热膨胀系数为α，均匀增加的温度ΔT作用于输液管道上。

首先要考虑弯曲变形对轴向力和热膨胀的影响，根据能量原理可得输液管道的势能为

(1)

(2)

其中αEAΔT为热轴力项，由于温度均匀增加，所以热弯矩值为零。由于液体流速达到超临界，从而忽略温度变化对输液管道内液体的影响。

管道的动能

(3)

流体的动能

(4)

通过上述方程我们可以利用Hamilton原理

(5)

把方程(1)～(4)代入Hamilton方程(5)中得横向运动方程

(6)

图1 输液管道模型图

为了简化方程(6)引入无量纲量

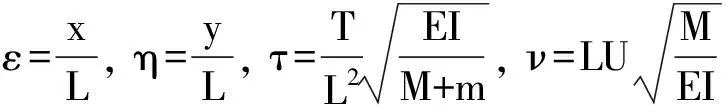
(7)

将方程(7)代入方程(6)中得到简化后的方程

(8)

为了研究输液管的静态屈曲构型，通过方程(8)会有新的平衡解，即横向位移不依赖于时间，所以η的解满足如下方程

(9)

上述方程中ψ为热轴力，与温度增加量ΔT有关，ν为液体流速，δ2/ 2 为非线性系数。

其中ξ为常数，方程(9)改写为

η(4)+λ2η″=0

(10)

其中λ2=υ2+φ-ξ

(11)

方程(10)是一个四阶常微分方程，通解为

η=C1+C2ε+C3cosλε+C4sinλε

(12)

其中Ci(i=1,2,3,4)是常数,根据两端简支热管的边界条件

η(0,τ)=0，η(1,τ)=0，η,εε(0,τ)=0，η,εε(1,τ)=0

(13)

将边界条件代入常微分方程(10)可得相应的λ的特征方程

sinλ=0 或λ=mπ，m=1,2,3…

从而得到输液管道的静态屈曲构型表达式

η=Csin(mπε)

(14)

将表达式(14)代入(11)可以得到屈曲振幅C的表达式

(15)

将式(15)代入式(14)中得平衡位形方程

(16)

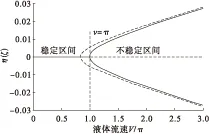
图2 两端铰支输液管在ε=0.75,φ=3,δ2/2=1

处一阶屈曲构型分叉图

图2为输液管道在ε=0.75(四分之三)处的屈曲振幅随液体流速的变化图，其中虚线代表的是输液管道在温度热膨胀状态下的振幅变化曲线，而实线代表无热膨胀作用时的振幅变化曲线。通过对比可以看出：无热膨胀作用下，当液体流速达到π时，输液管的曲线位形从零变为分岔状态；即当输液管内液体流速达到π时可认为达到临界状态，液体流速超过π为超临界状态。当温度均匀升高产生热膨胀时，从图5中可以看出在液体流速未达到π时，输液管振幅即达到临界状态。

2 热膨胀状态下超临界固有频率的解析解

(17)

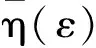
(18)

将铰支的边界条件(13)代入方程(18)得到

(19)

通过Galerkin截断的方法，将偏微分方程离散成常微分方程组:η(ε,τ)=φ(ε)eiωτ

其中ω是相应的自然频率，将上式代入方程(19)中，并将方程(19)进行Galerkin离散得

(20)

这里φ(ε)=sinλε，其中我们取λ=iπ且i=1，将方程(20)乘以相应的摸态函数φ(ε),并在(0,1)范围内积分得到

(21)

将振幅C的表达式代入方程(21)可得

(22)

(23)

式(23)为输液管道在液体流速达到超临界时的第一阶固有频率的解析式，该固有频率表达式与液体流速和温度变化有关，与非线性系数无关。

3 热膨胀对输液管道固有频率的影响

图3是两端铰支输液管在ε=0.75,φ=1处随液体流速的加快输液管道一阶固有频率的变化情况，并且对比了热膨胀对输液管道稳定性的影响。图3中虚线代表热膨胀状态下随液体流速增加输液管一阶固有频率的变化图，实线为理想状态下(无热膨胀作用)输液管一阶固有频率的变化图，通过对比可以看出热膨胀对输液管稳定性的影响。随着温度的升高，输液管道的稳定区间会减小，理想状态下液体流速达到π时固有频率由零状态发生屈曲变形，并随着流速的加快固有频率呈现指数增加，即流体流速达到π时固有频率达到一个临界点。而当温度均匀增加时，会对输液管道的固有频率产生影响从而导致临界速度点前移。

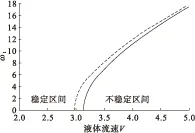
图3 热膨胀作用对超临界状态下一阶固有频率的影响图

4 结论

本文研究了热膨胀状态下输液管液体流速达到超临界时的非线性振动问题，运用Hamilton原理和Galerkin离散方法解输液管的非线性微分方程，分析了热膨胀和液体流速达到超临界时对输液管屈曲位形和一阶固有频率的影响。

在本文研究的模型中，通过解输液管一阶固有频率的表达式，可以得出输液管一阶固有频率与液体的流速和温度变化有关，而与非线性系数无关。在输液管液体流速增加时，输液管在热膨胀作用下会提前进入分叉状态，即在未达到超临界速度π时平衡位形就产生了屈曲变形。同理，通过计算输液管的一阶固有频率，并分析热膨胀对液体流速增加时的一阶固有频率的影响，得出了在热膨胀作用下输液管会提前发生屈曲变形，并使输液管的一阶固有频率更早地从零平衡状态发生屈曲变化，并随着液体流速的增加一阶固有频率增大。

[1]PAÏDOUSSIS M P,ISSID N T.Dynamic stability of pipes conveying fluid[J].Journal of Sound and Vibration,1974,33(3):267-294.

[2]PAIDOUSSIS M P.Flow induced instabilities of cylindrical structures[J].Applied Mechanics Reviews,1987,40(2):163.

[3]PAIDOUSSSIS M P,SEMLER C.Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid:a full nonlinear analysis[J].Nonlinear Dynamics,1993,4(6):655-670.

[4]SEMLER C,LI G X,PAÏDOUSSIS M P.The nonlinear equations of motion of pipes conveying fluid[J].Journal of Sound and Vibration,1994,169(5):577-599.

[5]倪樵,黄玉盈.非线性约束粘弹性输液管的动力特性分析[J].华中科技大学学报,2001,29(2):87-89.

[6]毛晓晔,丁虎,陈立群.3:1内共振下超临界输液管受迫振动响应[J].应用数学和力学,2016,37(4):345-351.

[7]YUAN L,GONG S F,JIN W L.Analysis on buckling performance of submarine pipelines during deepwater pipe-laying operation[J].China Ocean Engineering,2009,23(2):303-316.

[8]包日东,冯颖,毕文军.弹性支承输流管道的动力学特性[J].机械设计与制造,2010(3):129-131.

[9]荆红英,金基铎,闻邦椿.一端固定具有中间支承输流管道临界流速及稳定性分析[J].机械工程学报,2009,45(3):89-93.

[10]HOLMES P J.Bifurcations to divergence and flutter in flowIinduced oscillations:a finite dimensional analysis[J].Journal of Sound and Vibration,1977,53(4):471-503.

[11]HOLMES P J.Pipes supported at both ends cannot Flutter[J].ASME Journal of Applied Mechanics,1978,45(3):619-622.

[12]黄洪昌,杨运强,李君兰,等.航天器太阳电池阵热-结构分析研究进展[J].电 子 机 械 工 程，2012,28(4):1-7.

[13]LI J L,YAN S Z.Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit[J].Applied Thermal Engineering,2014,71(1):419-423.

[14]程乐锦,薛明德,唐羽烨,等.大型空间结构的热-结构动力学分析[J].应 用 力 学 学 报,2004,21(2):1-9.

[15]吴晓,张龙庭,马建勋.弹性直杆热膨胀状态下的非线性振动[J].工程力学学报,1996,13(4)：129-134.

[16]QIAN Q,WANG L,NI Q.Instability of simply supported pipes conveying fluid under thermal loads[J].Mechanics Research Communications,2009,36(3):413-417.

[17]缪旭,金基铎,杨天智.输流管道的超临界固有频率分析[J].沈阳航空航天大学学报,2013,30(4):28-31.

(责任编辑：吴萍 英文审校：赵欢)

The super critical vibration of the fluid-conveying pipe in the thermal expansion

LI Yang,FANG Bo

(Faculty of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China)

The paper dealt with the variation on buckling distortion and natural frequency of the fluid-conveying pipe subjected to thermal expansion with the acceleration of the fluid velocity by using Euler beams model applied in engineering practice.The curve equilibrium differential equation of the fluid-conveying pipe was deduced by Hamilton principle,and the buckling deformation of the fluid-conveying pipe under thermal expansion was analyzed.By using the Galerkin Discretization method,the analytical solution to the first-order natural frequency of the fluid-conveying pipe in thermal expansion was obtained when the flow speed of fluid exceeded the critical value.Thermal expansion of the fluid-conveying pipe affected the buckling configurations and the first-order natural frequency of the pipe,which was compared with that of corresponding flow speed of the fluid-conveying pipe reaching the super-critical value.

supercritical;thermal expansion;nonlinear vibration;frequency

2016-09-12

大连理工大学工业装备结构分析国家重点实验室基金(项目编号：GZ15209)

李阳(1990-)，男，辽宁朝阳人，硕士研究生，主要研究方向：:非线性动力学与结构振动，E-mail：1134797735 @qq.com；方勃(1964-)，男，辽宁沈阳人，教授，主要研究方向:非线性动力学与结构振动，E-mail:bfang0825@163.com。

2095-1248(2016)05-0024-04

O322

A

10.3969/j.issn.2095-1248.2016.05.005