全变换半群的极大子左(右)群

金久林，游泰杰，孙 艳，孙泽香

(贵州师范大学 数学科学学院,贵州 贵阳 550025)



全变换半群的极大子左(右)群

金久林，游泰杰，孙 艳，孙泽香

(贵州师范大学 数学科学学院,贵州 贵阳 550025)

设Xn={1,2,…,n}并赋予自然数序，Tn是Xn上的全变换半群。考虑Tn的子左(右)群的结构，证明了Tn的子半群是极大子左(右)群的充分必要条件，并得到了Tn的极大子左群的一些计数结果。

变换半群；极大子左群；极大子右群；左群；右群

0 引言

设S是一个半群，L,R,D,H,J表示S的Green关系，若R=S×S,则称S是右单的;对偶地，若L=S×S，则称S是左单的; 若(∀a,b,c∈S)ac=bc⟹a=b，则称S满足右消去律;若(∀a,b,c∈S)ca=cb⟹a=b,则称S满足左消去律。

设Xn={1,2,…,n}并赋予自然数序，Tn是Xn上的全变换半群。变换半群的具有某种性质的极大子半群的研究一直都是半群理论研究中的热点之一[1-6]。2002年, You[1]得到了全变换半群和部分变换半群的所有理想的极大正则子半群; 2003年，Yang[2]得到了全变换半群的理想的极大子半群;2001年，Yang[3]得到了有限奇异变换半群的极大子半群的完全分类;近年来，高[4]研究了保序压缩变换半群的理想的极大子半群; Xu[5]研究了有限部分变换半群的具有某种性质的极大子半群; 赵[6]得到了方向保序变换半群的极大正则子半群。本文在这些基础上, 考虑全变换半群的子左(右)群, 得到了Tn的极大子左群和极大子右群的结构, 并讨论其一些计数。

J M Howie[7]描述了Tn的Green关系：对任意α,β∈Tn，有

αLβ⟺im α=im β

αRβ⟺ker α=ker β

αJβ⟺|im α|=|im β|

D=J

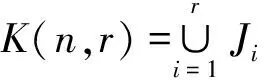
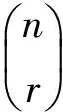
S(n,1)=S(n,n), S(n,r)=S(n-1,r-1)+rS(n-1,r)。

Tn的理想构成一个链，即K(n,1)⊂K(n,2)⊂…⊂K(n,n-1)⊂K(n,n)=Tn。 Tn的每个主因子是一个Rees商半群K(n,r)/K(n,r-1)，记为Pr。为方便，令Pr=Jr∪{0}, 其乘法定义为

Pr对上述乘法构成一个完全0-单半群。

关于完全0-单半群，有如下熟知的事实：

引理1 设x,y是完全0-单半群中的两个非零元，则xy≠0当且仅当Lx∩Ry包含一个幂等元。此时，xy∈Ly∩Rx。

定义1 设S是Tn的子半群，若S是左(右)单的，且满足右(左)消去律，则称S是Tn的子左(右)群。

定义2 设S是Tn的子左(右)群(S⊂Tn)，若S满足：对Tn的任意子左(右)群T,有S⊆T⟹S=T, 则称S是Tn的极大子左(右)群。

设S是一个半群，W是S的非空子集, 通常用E(W)表示W的幂等元集合, 对任意α∈S,Lα,Rα,Hα分别表示α所在的L-类、R-类、H-类。

本文未定义的术语及记法参见文献[9,10]。

1 主要结果及证明

引理2 设S是Tn的子半群，则α是S的幂等元的充要条件是对任意x∈im α，有x∈xα-1。

引理2可由幂等元的性质直接得到。

引理3[9]设G是一个有限群，则G的任一元阶都整除G的阶。

引理4[7]设e是半群S的一个幂等元，则He是S的子群。

引理5 设α∈He，其中e∈E(Tn)，则存在k∈N,使得αk=e。

证明 由引理4得到，He是Tn的子群。令|He|=k，由引理3得到，对任意α∈He，有αk=e。

引理6 设S是Tn的子半群，若对任意α,β∈S,im α=im β，则S是Tn的正则子半群。

证明 设S是Tn的子半群，若对任意α,β∈S, im α=im β，则im α=im β=im(αβ)，即αβ∈Lβ。由ker α⊆ ker(αβ)与Xn的有限性，知ker α=ker(αβ)，即αβ∈Rα。从而αβ∈Rα∩Lβ,再由引理1可知，Rβ∩Lα包含一个幂等元，即存在e∈E(Lα),使得e∈Rβ∩Lα=Rβ∩Lβ=Hβ。从而β∈S∩He，其中e∈E(Lα)。由引理4及引理5可得，存在k∈N使得βk=e,若k∈N*{1},由S是一个半群可知，βk-1∈S,特别地，若k=1，取βk-1=e,则βk-1=e=β∈S,从而存在βk-1∈S,k∈N*,使得ββk-1β=βkβ=eβ=β

则β是正则元。由β的任意性得到，S是Tn的正则子半群。

引理7 设S是Tn的子半群，若对任意α,β∈S, ker α=ker β，则S是Tn的正则子半群。

证明类似于引理6。

引理8 设S是Tn的子半群，若对任意α,β∈S,im α=im β，则E(S)是左零半群。

证明 设S是Tn的子半群，若对任意α,β∈S,im α=im β，则任取e,f∈E(S), 有 im e=im f。从而e,f有如下表示：

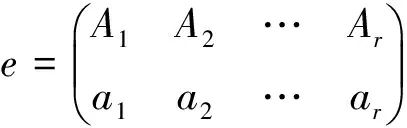
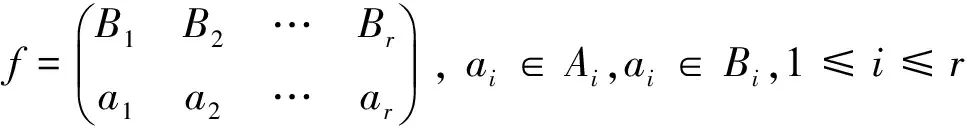
容易验证ef=e。因此,E(S)是左零半群。

引理9 设S是一个半群，若对任意α,β∈S， ker α=ker β，则E(S)是右零半群。

证明类似于引理8。

引理10[7]设S是一个半群，则以下条件等价：

1)E(S)是左(右)零半群，并且S是正则的；

2)S是左(右)单的，并且S满足右(左)消去律；

3)S是一个左(右)群；

下面给出本文主要结果及证明：

定理1 设S是Tn的子半群, 则

1) S是Tn的子左群的充要条件是对任意α,β∈S，im α=im β;

2) S是Tn的子右群的充要条件是对任意α,β∈S，ker α=ker β;

证明 1)充分性：由引理6、引理8、引理10可以得到, S是Tn的子左群。

必要性：若S是Tn的子左群, 由引理10, 知L=S×S，即对任意α,β∈S，im α=im β。

2)充分性：由引理7、引理9、引理10可以得到,S是Tn的子右群。

必要性: 若S是Tn的子右群, 由引理10 ,知R=S×S, 即对任意α,β∈S，ker α=ker β。

定理2 1)Tn的极大子左群有且仅有如下形式：

(*)

2)Tn的极大子左群有且仅有如下形式：

证明 1)充分性:设α∈Tn,LG(α)=∪e∈E(Lα)He。对任意β,γ∈LG(α), 则存在e,f∈E(Lα), 使得β∈He且γ∈Hf, 易见im β=im γ, 即βLγ。于是Hγ=Rγ∩Lγ=Rγ∩Lβ, 从而Rγ∩Lβ包含幂等元f, 由引理1得到, βγ∈Rβ∩Lγ=Rβ∩Lβ=Hβ=He⊆LG(α), 再由定理1可得, LG(α)是Tn的子左群。下证LG(α)的极大性。

设对Tn的任意子左群T, 有LG(α)⊆T。若LG(α)⊂T, 则存在ε∈TLG(α), 从而Hε∩E(Lα)=∅, 注意到, T是Tn的子左群, 由定理1可得, 对任意η∈T, 有im ε=im η, 即ε Lη, 于是Hε=Rε∩Lε=Rε∩Lη, 从而Rε∩Lη∩E(Lα)=∅, 由引理1可得, ηε=0, 从而|im(ηε)|<|im ε|，这与T是Tn的子左群矛盾。因此, T=LG(α)。

必要性：假设M是Tn的极大子左群, 但不是定理2中(*)的形式, 从而存在β∈M, 使得Hβ∩E(Lβ)=∅(否则, 若对任意β∈M, 有Hβ∩E(Lβ)≠∅, 即存在e∈E(Lβ), 使得β∈He, 则M⊆LG(β), 由M是Tn的极大子左群, 知M=LG(β), 这与假设矛盾)。注意到, M是Tn的子左群, 由定理1得到, M⊆Lβ, 即对任意γ∈M, 有βLγ, 于是Hβ=Rβ∩Lβ=Rβ∩Lγ, 从而Rβ∩Lγ∩E(Lβ)=∅, 由引理1可得, γβ=0, 从而|im(γβ)|<|im β|，这与M是Tn的极大子左群矛盾。

因此, Tn的极大子左群有且仅有定理中(*)的形式。

2)证明类似于(1)。

由定理2可直接得到：

推论1 设A⊆Xn且A≠∅，则Tn的极大子左群有且仅有如下形式：

LTn(A)={α∈Tn:Aα=A,(XnA)α⊆A}。

定理3 几个组合结果：

1)设1≤r≤n-1, A⊆Xn且|A|=r，则

2)Tn的极大子左群共有2n-1个。

3)在同构意义下, Tn的极大子左群共有n个。

证明 1)设1≤r≤n-1, A⊆Xn且|A|=r, 由推论1可知, Tn的极大子左群可表示为LTn(A)={α∈Tn:Aα=A,(XnA)α⊆A}。对任意α∈LTn(A), 若将其原象按自然数的序排列, 则α由其象元素的排列唯一确定。考虑两种情形：

…

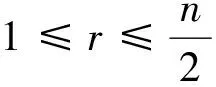
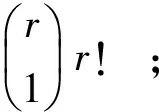
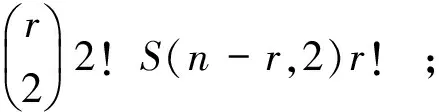
以此类推, 有

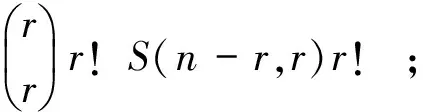
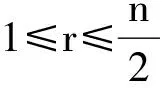
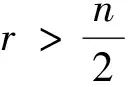
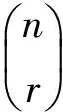
3)设A,B⊆Xn且|A|=|B|=r。由推论1可知, Tn的极大子左群可表示为

LTn(A)={α∈Tn:Aα=A,(XnA)α⊆A}

设f是A到B的双射, g是XnA到XnB的双射。对任意α∈LTn(A), 定义

定义映射φ:LTn(A)→LTn(B)。验证φ是同构映射, 可参见文献[10]由此可见，LTn(A)与LTn(B)同构。即在同一个J-类上的极大子左群同构。

因此, 在同构意义下, Tn的极大子左群共有n个。

注 在定理3(1)中, 当A=Xn时, |LTn(A)|=|Sn|=n!(Sn是对称群)。

[1] YOU T J.Maximal Regular Subsemigroup of Certain Semigroup of Transformation[J].Semigroup Forum,2002,64:391-396.

[2] YANG H B,YANG X L.Maximal Subsemigroups of Finite Transformation Semigroups K(n,r)[J].Acta Mathematica Sinica,2004,20(3):475-482.

[3] YANG X L.Maximal Subsemigroups of the Finite Transformation Semigroup[J].Communications in Algebra,2001,29(3):1175-1182.

[4] 高荣海,喻秉钧.保序压缩变换半群的理想的极大子半群[J].四川师范大学学报(自然科学版),2014,37(5)：643-648.

[5] 徐波,赵平,李俊扬.有限部分保序变换半群的具有某种性质的极大子半群(英)[J].数学杂志,2010，39(4)：617-621.

[6] 赵平,游泰杰,徐波.方向保序变换半群的极大正则子半群[J].吉林大学学报(理学版),2011,49(2)：203-206.

[7] HOWIE J M.Fundamentals of Semigroup Theory[M].London:Oxford Press,1995.

[8] 胡端平,鲁晓成.组合数学[M].武汉：武汉大学出版社,2001.

[9] 王鄂芳.有限群论基础(第2版)[M].北京：清华大学出版社,2012.

[10]高荣海.具有稳定子集的奇异变换半群的结构与性质[D/OL].贵阳：贵州师范大学,2009.[2016-03-20].http://epub.cnki.net/kns/brief/result/aspx.

Maximal left (right) group of the full transformation semigroup

JIN Jiulin,YOU Taijie,SUN Yan,SUN Zexiang

(School of Mathematical Science,Guizhou Normal University,Guiyang,Guizhou 550025,China)

Let Xn={1,2,…,n}, and it has the order of natural numbers, Tnbe the full transformation semigroup on Xn. Consider left (right) group structure of Tn, the sufficient and necessary condition of subsemigroup of Tnis maximal left (right) group is proved, and get some counting results of maximal left group of Tn.

transformation semigroup; maximal left group; maximal right group; left group; right group

1004—5570(2016)06-0052-04

2016-05-10

金久林(1991-),男,硕士研究生,研究方向:半群理论及编码理论,E-mail:1358724098@qq.com.

O152.7

A