ADI-FDTD方法在乳腺癌检测正向计算中的应用

陈碧云 张业荣 潘鑫

(1.南京邮电大学电子科学与工程学院,南京 210003;2.空军航空大学,阜新 123000)



ADI-FDTD方法在乳腺癌检测正向计算中的应用

陈碧云1张业荣1潘鑫2

(1.南京邮电大学电子科学与工程学院,南京 210003;2.空军航空大学,阜新 123000)

传统的时域有限差分(Finite-Difference Time-Domain, FDTD)算法受到稳定性条件的制约,时间步长受限于空间网格的尺寸.医学应用讲究即时性,为提高成像的速度, 文中采用无条件稳定的交替隐式时域有限差分(Alternating-Direction Implicit Finite-Difference Time-Domain, ADI-FDTD)算法替代传统的FDTD算法进行正向计算,通过实验得出采用 ADI-FDTD算法在保证精度的前提下,计算时间可缩短为FDTD算法的四分之一,为乳腺癌微波即时成像提供了可能.

交替隐式时域有限差分法;微波断层成像;乳腺癌

DOI 10.13443/j.cjors.2016013101

引 言

微波成像技术作为一种新型的乳腺癌检测手段,因低风险、高灵敏度和高对比度等一系列优点而日益受到重视[1-2].相比于乳腺钼靶X线检查,微波的能量仅为几个电子伏特,消除了对人体的健康隐患,同时非侵入式的检查手段不会给人带来不适;相比于磁共振成像(Magnetic Resonance Imaging, MRI)和正电子发射计算机断层显像(Positron Emission Computed Tomography,PECT),微波成像的低成本为普查提供了可能;相比于多普勒超声成像,微波对肿瘤尤其是恶性肿瘤具有更高的敏感度,检出率更高[3].

国内外研究乳腺癌微波成像主要集中在两种方法：一种是共焦成像(Confocal Microwave Imaging, CMI)[4-7]；另一种是断层成像(Microwave Tomography, MWT)[8-13].MWT类似于现代医用中的CT,相比于CMI,其物理解释更清晰,更具医学诊断价值.MWT属于电磁逆散射的研究范畴,处理逆散射问题通常采用最优化迭代求解,大量的时间耗费在重复的正向计算,因此在保证精度的前提下提高正向计算的效率应该成为我们关注的焦点.

目前MWT的研究主要集中在频域范围内,最早的临床系统是由Meaney 等人[8]于2000年开发出的一套基于牛顿高斯迭代法微波断层成像系统,采用有限元法(Finite Element Method,FEM)算法和边界元(Boundary Element Method,BEM)算法相结合进行正向计算,然而由于频带的限制,获得的分辨率不高,后来Rubk等[9]在Meaney研究的基础上,将二维成像扩展到了三维,采用矩量法(Method of Moments,MOM)进行前向计算,然而三维成像时间过长,一次成像需要几十个小时,为此Liu等[10]采用快速傅里叶变换(Fast Fourier Transform,FFT)算法还原了二维和三维参数分布.

针对乳腺癌成像,选择时域方法更有优势:1)早期的乳腺肿瘤是毫米级的,利用宽带高频脉冲信号能够提供较好的成像分辨率;2)时域MWT利用目标的瞬态响应波形进行成像,包含的信息量更多,成像结果更准确[14].Takenaka等人采用时域逆散射算法对二维乳腺癌模型进行了图像重建[11],刘广东等人以LM算法为基础,分别对二维半圆形乳房[12]和三维半球乳房[13]模型进行了时域断层成像分析,这些算法的成像分辨率以及鲁棒性都很好,然而临床应用普遍存在一大缺陷——成像时间过长,尤其是到了高维情形.

早期在时域上研究乳腺癌微波成像普遍采用了FDTD算法,作为经典的电磁三大算法之一,FDTD被广泛地运用于电磁学的各个领域[15-16].然而传统的FDTD算法要满足柯朗-弗里德里希斯-列维(Courant-Friedrichs-Lewy,CFL)条件,时间步长受限于空间网格的大小,成像时想要得到比较好的分辨率,CPU的运算时间将要大大增加.临床应用时,检测的效率和速度不佳,因此我们需要寻找更加高效的算法来提高计算效率.近些年,ADI-FDTD算法引起了越来越多的关注[17-18],相对于传统的FDTD方法,ADI-FDTD采用了交替隐式差分方法,时间步长不再受到CFL条件的制约,在保证精确度的前提下可以大大降低运算成本.

本文首次将ADI-FDTD算法应用到二维乳腺癌模型中,仿真实验采用二维半圆无限长柱状乳房模型,分别对单个圆形,单个“十”字型和多个“十”字型的肿瘤模型进行仿真测试,实验结果与传统的FDTD方法进行了比较,从而验证了ADI-FDTD算法的可行性与有效性.

1 理论分析

乳房组织是非磁性介质,磁导率σm=0,二维TM波在乳房组织中传播满足如下麦克斯韦方程:

(1)

(2)

(3)

式中：r=(x,y)T表示位置矢量;ε(r)表示介电常数;σ(r)为电导率;μ0为真空中的磁导率;Ez(r,t)表示电场在z轴上的分量;Hx(r,t)和Hy(r,t)分别为磁场强度在x轴和y轴上的分量.M根发射天线和N根接收天线分别位于r=rm(m=1,2,…,M)和r=rn(n=1,2,…,N)如图1黑色实心点处.

微波断层成像技术是利用电磁脉冲照射下产生的散射场,反演出目标物体的电参数分布.通常采取的方案是将逆散射问题转化为最优化问题进行迭代求解,基于最小二乘法构建如下代价函数:

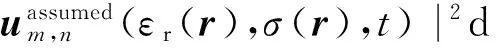
(4)

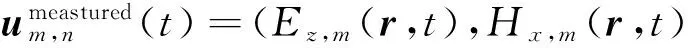
Hy,m(r,t))T;

(5)

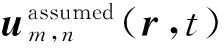
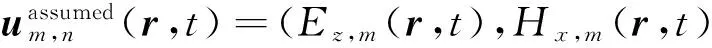
Hy,m(r,t))T.

(6)

1) 第一步n→n+1/2对方程中的x方向导数取隐式差分格式,对y方向导数取显示,整理得:

(7)

(8)

(9)

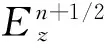
第二步n+1/2→n+1,对方程中的y方向导数取隐式差分格式,对x方向导数取显示,整理得:

(10)

(11)

(12)

求解类似于第一步,这里不再赘述.ADI-FDTD算法提供无条件稳定,时间步长的选择不再受限于空间网格的大小,计算时间就可以被大大的缩短.

2 建模

建立二维半无限长圆柱体乳房模型如图1,假设该模型浸没在各向同性的耦合溶液中,该耦合溶液的电参数为εr=36,σ=0 S/m,与皮肤层的波阻抗匹配,乳房结构简化为一个半圆形的无限长圆柱体,最外层是厚度为2 mm的皮肤层,其电磁参数为εr=36,σ=1.0 S/m.皮肤层下面是乳房组织层,是一个半径为50 mm的半圆柱体,电参数为εr=9.0,σ=0.15 S/m,连接乳房层的是一个20 mm厚的胸壁层,电参数为εr=50,σ=1.2 S/m.成像系统由距离皮肤表面8 mm放置的9根天线组成,9发8收(当其中一根作为发射天线时,其余8根作为接收天线, 收发天线位置见图 1中的黑色圆点,作为发射天线时从左往右依次标记为天线T1,天线T2,…,天线T9,同样地接收天线从左往右依次标记为天线R1,天线R2,…,天线R8).

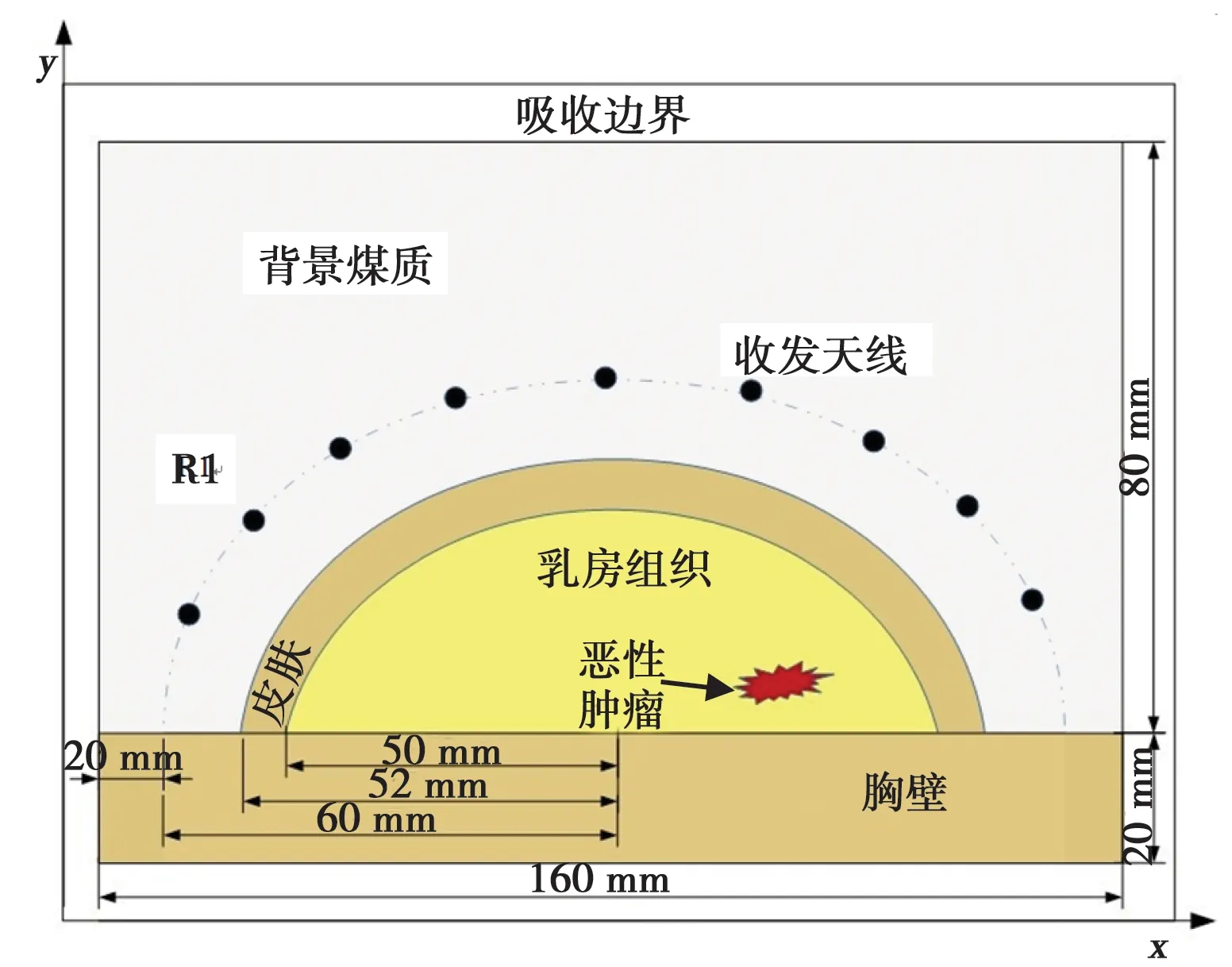
图1 乳房结构模型图

激励源选取调制高斯脉冲,其时域表达式为

(13)

式中：fc为中心频率,取2.0 GHz;τ为高斯脉冲的宽度,取1.436×10-9s;t0=1.288×10-9s.整个计算区域采用均匀网格剖分,由于Mur吸收条件推导比较简单,在ADI-FDTD方法的运用中较为普遍,因此此处截断边界采用一阶Mur吸收边界,传统FDTD计算步长要满足CFL条件:

(14)

这里取ΔtFDTD=Δx/(2c),ADI-FDTD 时间步长ΔtADI-FDTD=CFL*ΔtFDTD,这里取两者相差的系数为CFL是为了突出ADI-FDTD与FDTD算法的区别, 这里CFL取整数.

3 仿真结果与讨论

3.1 情形1

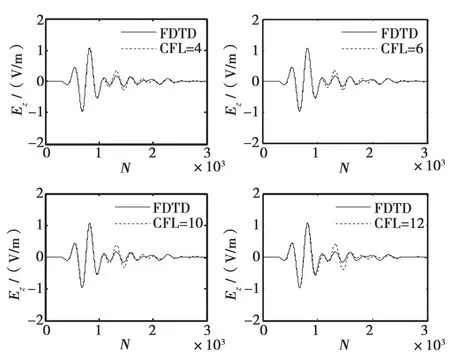
元胞尺寸取Δx=Δy=1 mm,位于点(52,20)有一个半径大小为3 mm圆形肿瘤,接下来分别采用FDTD方法和ADI-FDTD方法进行仿真实验,FDTD时间步数Nmax取3 000,CFL取4,6,10,12,天线T1上放置激励源,天线R1上接收的电磁场如图2(a),图2(b)和图2(c)所示.

(a) Ez

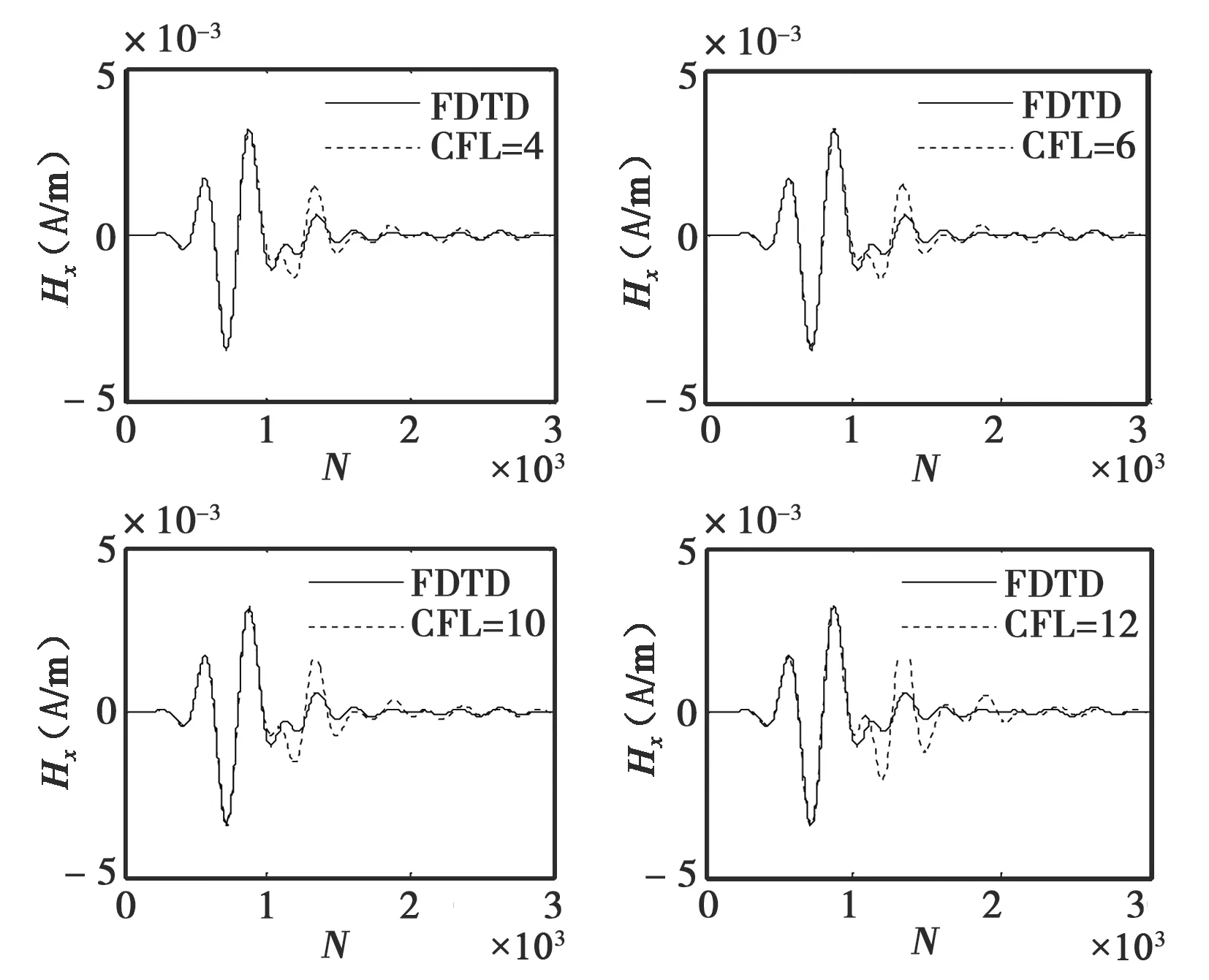
(b) Hx

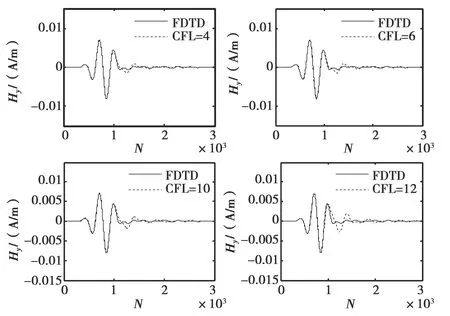
(c) Hy图2 情形1(天线R1上接收到的场)

本文采用ADI-FDTD方法进行前向计算,所涉及的信号是时域波形,相比频域方法,时域波形由于包含了更多的信息,包括时间、强度以及相位,可能获得更准确的重建结果．从图2(a),图2(b)和图2(c)仿真结果我们可以看出,ADI-FDTD的计算结果与FDTD基本一致,只是在后期出现了一些振荡,产生这种振荡的主要原因有二:一是采用的吸收边界条件所引起的反射误差;二是离散网格过程中阶梯误差,传统的FDTD方法中也有相应缺陷.同时也看到随着CFL数值的增加,出现的振荡越明显,因为Δt越大所带来的数值色散误差也越大,所以说CFL的选取还是有约束的.

表1中,T表示进行一次正向计算的时间,TADI-FDTD/TFDTD表示采用ADI-FDTD方法与FDTD方法的时间比,从表1我们可以发现从CFL=4开始,采用ADI-FDTD的时间比FDTD短,当CFL=12,采用ADI-FDTD计算时间仅为FDTD方法的24.9%,计算时间大大的缩短.

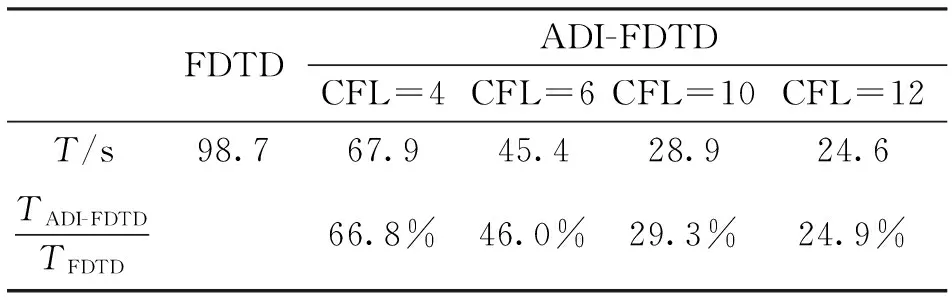
表1 情形1ADI-FDTD与FDTD计算时间比较

3.2 情形2

肿瘤大多都是不光滑的,为了更加接近真实,采用“+”字形肿瘤模型,元胞的尺寸选取为Δx=Δy=2 mm,位于(90,30)存在一个由5个边长为2 mm的方柱组成的“+”字型肿瘤.分别采用了FDTD方法和ADI-FDTD方法进行实验, FDTD时间步数Nmax取1 500,天线T1上放置激励源,天线R1上接收的电磁场如图3(a),图3(b)和图3(c)所示.

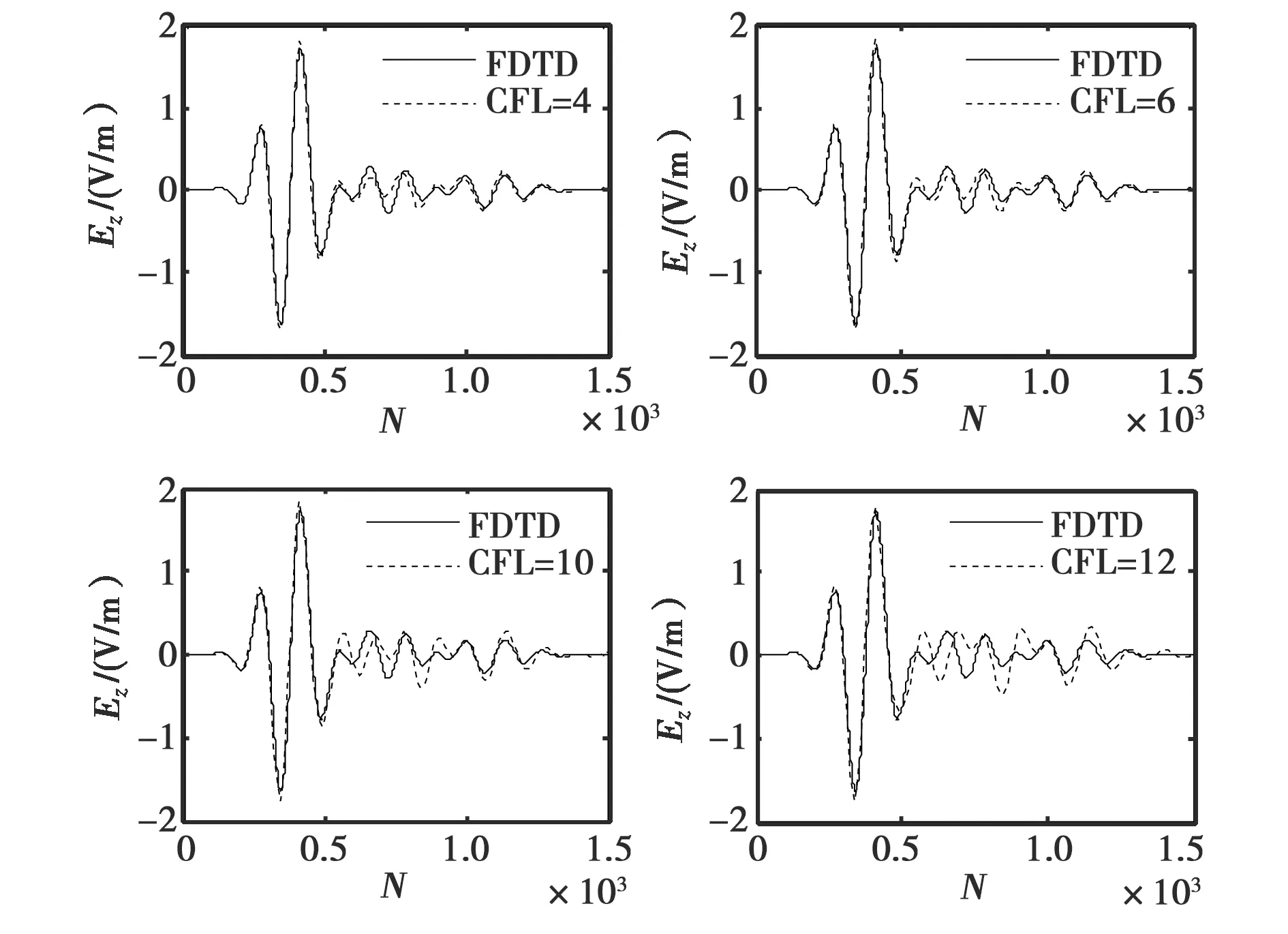
(a) Ez

(b) Hx

(c) Hy图3 情形2(R1上接收到的场)

从图3(a),图3(b)和图3(c)仿真结果我们可以看出,CFL取4,6,10,12时,FDTD和ADI-FDTD的计算结果还是比较接近的,整个起伏的走势表现一致,除了后期出现少许振荡.同时比较情形1和情形2,我们可以看出情形1取1 mm的误差要小于情形2取2 mm时产生的误差,网格剖分越细,误差越小,至于这种误差对于成像精度的影响,在后期要结合成像结果进行分析,本文暂不做讨论．

从表2我们发现,同样的从CFL=6开始,ADI-FDTD的计算优势开始体现,当CFL=12时,采用ADI-FDTD方法的计算时间为FDTD的54.52%.比较表1和表2还可以发现,采用1 mm剖分网格的计算效率要高于2 mm的情形,同样当CFL=12,采用1 mm网格的计算时间仅为传统FDTD的24.9%,采用2 mm网格的计算时间为传统FDTD方法的54.4%,从而可以得出采用ADI-FDTD方法另一个好处就是,分辨率越高,计算效率越高,这于成像是非常有利的.

表2 情形2ADI-FDTD与FDTD计算时间比较

3.3 情形3

存在多个肿瘤的情形,位于(90,30)和(52,20)处分别有一个5个边长为2 mm的方柱组成的“十”字形柱体肿瘤,元胞尺寸取Δx=Δy=2 mm.仿真分别采用FDTD方法和ADI-FDTD方法进行实验,接下来分别采用FDTD方法和ADI-FDTD方法进行仿真实验,FDTD时间步数取1 500,天线T1上放置激励源,天线R1上接收的电磁场如图4(a),图4(b)和图4(c)所示.

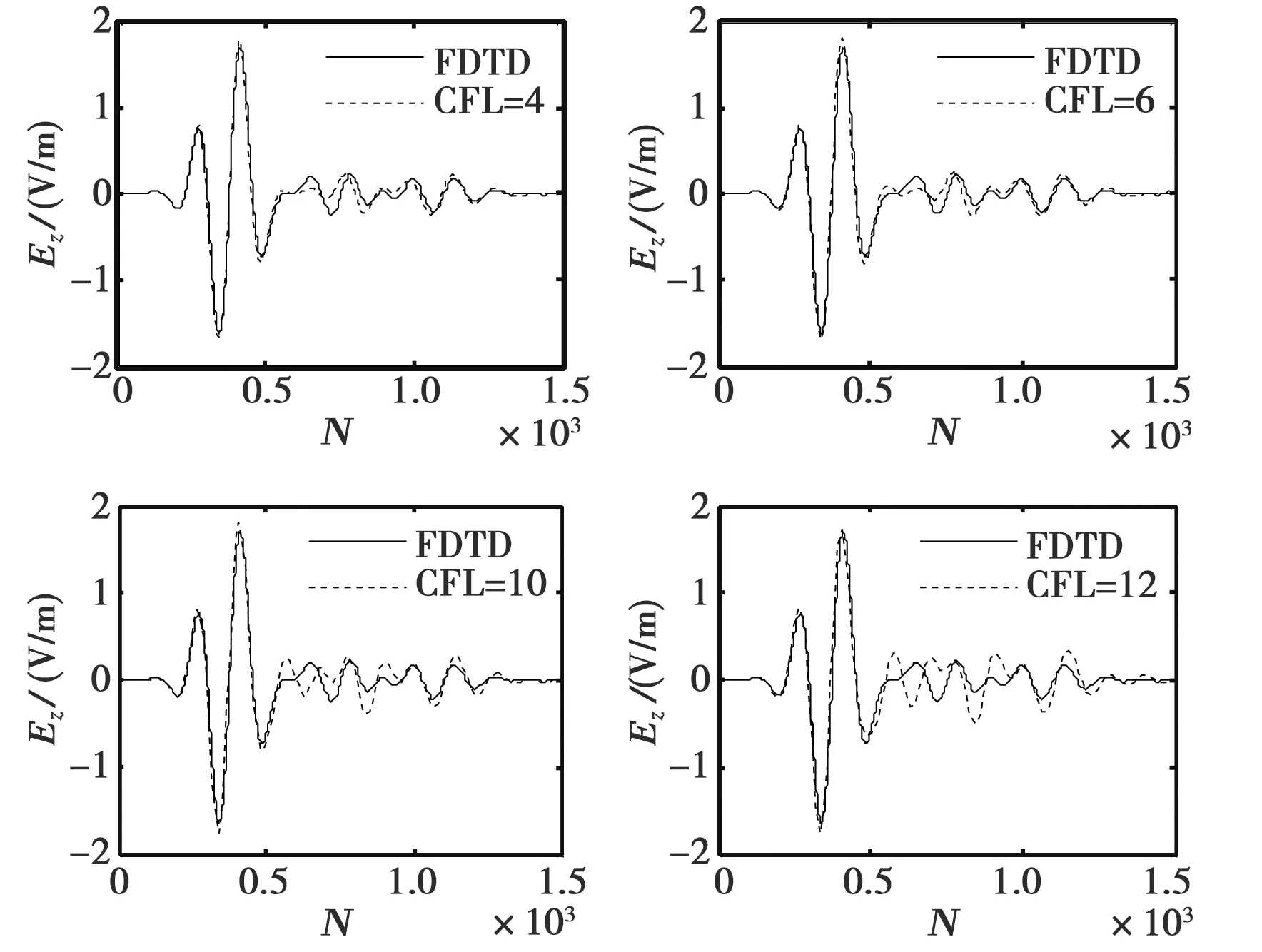
(a) Ez

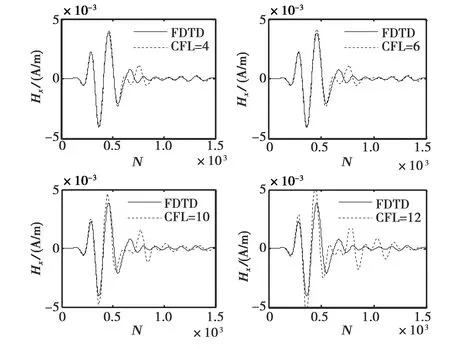
(b) Hx

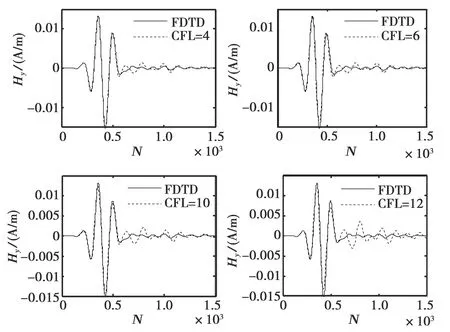
(c) Hy图4 情形3(R1上接收到的场)

从图4(a),图4(b)和图4(c)仿真结果我们可以看出,FDTD和ADI-FDTD的计算结果同样吻合得很好,多个肿瘤时采用ADI-FDTD的计算结果同样可行,说明ADI-FDTD对于乳腺癌成像的适用性很好,为我们进一步的成像研究奠定了基础.

4 结 论

对乳腺癌这种高对比问题进行微波断层成像,采用传统的FDTD算法进行分析时,由于受到CFL稳定性条件的制约,时间步长受限于空间间隔的大小,计算时间过长,尤其是在高维情形下更为明显.

为了提高检测的效率,增强成像的临床实用性,本文采用ADI-FDTD方法代替传统的FDTD方法进行前向计算,适当地增加时间步长,缩短计算时间,采用二维半圆无限长柱状乳房模型,分别对单个圆形、单个“十”字型和多个“十”字型的肿瘤模型进行了测试,通过实验得出：1) 采用ADI-FDTD算法所得的结果和传统FDTD吻合地很好,在保证现有成像精度的同时,大大缩短了成像时间,提供了即时成像的可能性;2) 当网格剖分越细时,ADI-FDTD所体现出的效率越高,这于高精度成像是非常有利的,大大地提高了微波断层成像技术的临床可应用性.

本文所做的研究内容是前期的正向计算,为后续的成像问题奠定了基础,下一步的工作就是将ADI-FDTD方法运用于成像分析中.当然前期的工作还有一些问题需要考虑,比如说边界条件的选取、天线的具体设计、激励源的选择等等,这些也是我们在今后的研究过程中所需考虑的实际问题.

[1]FEAR E C.Microwave imaging of the breast[J].Technology in cancer research &treatment, 2005, 4(1)：69-82.

[2]LIU G D, ZHANG Y R.An overview of active microwave imaging for early breast cancer detection [J].

Journal of Nanjing University of Posts and Telecommunications, 2010, 30(1)：64-70.

[3]BIN GUO.Microwave techniques for breast cancer detection and treatment [D].Gainesville：University of Florida, 2007.

[4]HAGNESS S C, TAFLOVE A, BRIDGES J E.Two-dimensional FDTD analysis of a pulsed microwave confocal system for breast cancer detection：fixed-focus and antenna-array sensors[J].IEEE transactions on biomedical engineering, 1999, 47(5)：783-791.

[5]FEAR E C, L XU, HAGNESS S C.Confocal microwave imaging for breast cancer detection：localization of tumors in three dimensions[J].IEEE transactions on biomedical engineering, 2002, 49(8)：812-822.

[6]LI X, HAGNESS S C.A confocal microwave imaging algorithm for breast cancer detection[J].IEEE Microwave and wireless components letters, 2001, 11(3)：130-132.

[7]BOND E J, LI X, HAGNESS S C, et al.Microwave imaging via space-time beam-forming for early detection of breast cancer[J].IEEE transactions on antennas and propagation, 2003, 51(8)：1690-1705.

[8]MEANEY P M, FANNING M W, LI D.A clinical prototype for active microwave imaging of the breast[J].IEEE transactions on microwave theory and techniques, 2000, 48(11)：1841-1853.

[9]RUBAK T, MEANEY P M, MEINCKE P.Nonlinear microwave imaging for breast-cancer screening using Gauss-Newton's method and the CGLS inversion algorithm[J].IEEE transactions on antennas and propagation, 2007, 55(8)：2320-2331.

[10]LIU Q H, YU C, STANG J.Experimental and numerical investigations of a high-resolution 3D microwave imaging system for breast cancer detection[C]//Antennas and Propagation Society International Symposium, 2007：2192.DOI：10.1109/APS.2007.4395963

[11]TAKENAKA T, JIA H, TANAKA T.Microwave imaging of electrical property distributions by a forward-backward time-stepping method[J].Journal of electromagnetic waves and applications, 2000, 14(12)：1609-1626.

[12]刘广东, 张业荣.二维有耗色散介质的时域逆散射方法[J].物理学报, 2010, 59(10):6969-6979.

LIU G D, ZHANG Y R.Time-domain inverse scattering problem for two-dimensional frequency-dispersive lossy media[J].Acta physica sinica, 2010, 59(10)：6969-6979.(in Chinese)

[13]刘广东, 张业荣.乳腺癌检测的三维时域微波断层成像方法[J].电波科学学报, 2010, 25(6)：1175-1181.

LIU G D, ZHANG Y R.Three-dimensional microwave tomography imaging method in the time-domain for detection of breast cancer[J].Chinese journal of radio science, 2010, 25(6)：1175-1181.(in Chinese)

[14]WINTERS D W, BOND E J, BARRY D V, et al.Estimation of the frequency-dependent average dielectric properties of breast tissue using a time-domain inverse scattering technique[J].IEEE transactions on antennas and propagation, 2006, 54(11)：3517-3528.

[15]唐涛, 廖成, 杨丹.FDTD求解高功率微波大气传播问题的可行性研究[J].电波科学学报, 2010, 25(1)：122-126.

TANG T, LIAO C, YANG D.Feasibility of solving high-power microwave propagation in the atmosphere using FDTD method[J].Chinese journal of radio science, 2010, 25(1)：122-126.(in Chinese)

[16]高本庆, 薛正辉, 任武.FDTD计算中关于低频激励源问题的研讨[J].电波科学学报, 2009, 24(2)：213-217.

GAO B Q, XUE Z H, REN W.Study on low frequency exciting source in FDTD simulation[J].Chinese journal of radio science, 2009, 24(2)：213-217.(in Chinese)

[17]WANG S, CHEN J.Multigrid ADI method for two-dimensional electromagnetic simulations[J].IEEE transactions on antennas propagation, 2006, 54(2)：715-720.

[18]张玉廷, 蔡智, 刘胜.交替隐式时域有限差分分析有耗介质电磁波传播[J].电波科学学报, 2011, 26(6)：1088-1094.

ZHANG Y T, CAI Z, LIU S.Electromagnetic wave propagation in loss media based on ADI-FDTD[J].Chinese journal of radio science, 2011, 26(6)：1088-1094.(in Chinese)

[19]汤炜, 李清亮, 焦培南, 等.ADI-FDTD在二维散射问题中的应用[J].电波科学学报, 2003, 18(6)：620-624.

TANG W, LI Q L, JIAO P N, et al.Two dimension scattering analysis using ADI-FDTD method[J].Chinese journal of radio science, 2003, 18(6)：620-624.(in Chinese)

陈碧云 (1986-),女,江苏人,南京邮电大学电子科学与工程学院博士生,主要研究方向为电波传播、电磁逆散射理论及其应用等．

张业荣 (1963-),男,安徽人,南京邮电大学电子科学与工程学院教授、博士生导师,主要研究方向为移动通信系统与设计、电磁逆散射、电磁场的数值计算和UWB信道等．

Application of ADI-FDTD method in the forward solver of early breast cancer detection

CHEN Biyun1ZHANG Yerong1PAN Xin2

(1.CollegeofElectronicScienceandEngineering,NanjingUniversityofPostsandTelecommunications,Nanjing210003,China;2.AviationUniversityofAirForce,Fuxin123000,China)

In the conventional finite-difference time-domain(FDTD) method, fine cells reduce the time-step size due to the Courant-Friedrich-Levy(CFL) stability condition, which results in an increase in computational effort, such as the central processing unit (CPU) time.In the alternating-direction implicit finite-difference time-domain(ADI-FDTD) method, a larger time-step size than allowed by the CFL stability condition limitation can be set because the algorithm of this method is unconditionally stable.Consequently, an increase in computational efforts caused by fine cells can be prevented.The simulation experiments data by the ADI-FDTD method were compared with that by the conventional FDTD method.The results show that simulation field by ADI-FDTD method agree quite well with that by the FDTD method, but the required CPU time can be much shorter than that for the FDTD method.

alternating-direction implicit finite-difference time-domain(ADI-FDTD);microwave tomography (MT);breast cancer

陈碧云, 张业荣, 潘鑫.ADI-FDTD方法在乳腺癌检测正向计算中的应用[J].电波科学学报,2016,31(5):1016-1022.

10.13443/j.cjors.2016013101

CHEN B Y, ZHANG Y R, PAN X.Application of ADI-FDTD method in the forward solver of early breast cancer detection [J].Chinese journal of radio science,2016,31(5):1016-1022.(in Chinese).DOI：10.13443/j.cjors.2016013101

2016-01-31

TN011

A

1005-0388(2016)05-1016-07

联系人：陈碧云 E-mail：cby8612@126.com.