基于粒子群算法的高斯过程建模对GPS天线优化设计研究

强哲 陈艺 田雨波 许兰

(江苏科技大学电子信息学院,镇江 212003)



基于粒子群算法的高斯过程建模对GPS天线优化设计研究

强哲 陈艺 田雨波 许兰

(江苏科技大学电子信息学院,镇江 212003)

目前微带天线的优化设计主要采用优化算法与电磁仿真软件HFSS相结合的方案,但使用HFSS进行大量的精确电磁仿真花费时间较长且对硬件要求较高．为解决此问题,提出了一种在优化过程中利用高斯过程模型替代全波电磁仿真软件的方法,并应用粒子群算法进行优化设计,这种方案可以有效减少优化设计所需时间．利用该方法对GPS北斗双模微带天线进行了优化设计,在花费时间只有原方法0.2%的基础上所设计的天线能够满足设计指标,证明了该方法的有效性．

高斯过程模型;PSO;GPS天线;HFSS

DOI 10.13443/j.cjors.2016052201

微带天线由于其体积小而且性能稳定等优点,在GPS系统中得到广泛的应用[1-3]．粒子群优化(Particle Swarm Optimization,PSO)算法与HFSS电磁仿真软件相结合的方案,近年来被应用于天线优化设计问题中,而且取得了不错的效果[4-5]．但是这种方案每次更新个体的位置和速度信息后都需要调用HFSS对个体进行评估,而这种评估的耗时较长,大大提高了计算成本,使得优化算法的实用性受到影响．因此,需要寻找一种建模方案替代调用HFSS的方法,达到节省时间的目的．高斯过程(Gaussian Process,GP)作为近年来快速发展的一种机器学习方法,对处理小样本、高维数、非线性等复杂问题有很好的适应性[6-8]．研究表明,GP模型可以作为天线设计中精确全波分析的一种快速替代方案,在保证模型精度的同时,大幅减少天线设计中精确仿真所需要的时间[9-11]．本文研究了一种使用GP模型作为PSO算法的适应度评价方案,并基于该方案对GPS北斗双模微带天线进行了优化设计,使其满足预设的设计指标．

1 基于粒子群算法的高斯过程模型

1.1 高斯过程模型

GP模型可以建立训练集输入X与输出y之间的映射关系,并根据此映射关系给出测试样本x*对应的预测值．

GP描述了一种函数分布,它是无限数量的随机变量组成的任意子集都符合联合高斯分布的集合,其性质可由均值函数和协方差函数决定,即

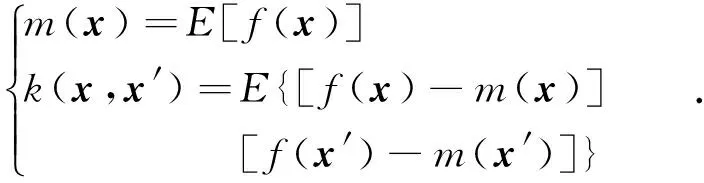
(1)

式中：x,x′∈Rd为任意d维矢量;m(x)和k(x,x′)分别表示均值函数和协方差函数．因此,GP可以表示为

f(x)～GP(m(x),k(x,x′))．

(2)

假设包含n个观测值的有限训练集D={(xi,yi)|i=1,2,…,n}=(X,y),其中X=[x1,x2,…,xn]表示n个d维训练输入矢量组成的d×n维训练输入矩阵,y=[y1,y2,…,yn]T表示相应的n个训练输出标量yi组成的训练输出矢量．模型可以表示为

y=f(x)+ε．

(3)

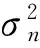
(4)

x为输入向量,y为受噪声污染的观测值,得到y的先验分布为

(5)

式中,K=K(X,X)为n×n阶对称正定协方差矩阵,矩阵元素用来度量xi与xj之间的相关性．n个训练样本输出y与n*个测试样本输出f*组成的联合高斯先验分布为

(6)

式中：K(X,X*)为n*个测试输出样本与n个训练输出样本之间的n×n*阶协方差矩阵;K(X*,X*)是测试输出样本自身的n*×n*阶协方差矩阵．

GP的协方差函数必须满足Mercer条件:对任一点集都能够保证产生一个非负正定协方差矩阵．本文采用ARD Matern 5/2协方差函数:

(7)

根据贝叶斯原理在训练集的基础上可以预测出与x*对应的最可能的输出值．采用贝叶斯原理的目的是利用观测到的真实数据不断更新概率预测分布,即给定新的输入x*、训练集的输入值X和观测目标值y的条件下,推断出y*的最大可能的预测后验分布:

(8)

式中:

(9)

为预测均值,给出了最有可能测试输出的值;

∑=K(X*,X*)-K(X*,X)(K(X,X)+

(10)

为协方差矩阵,给出了相应的预测方差．

1.2 粒子群优化算法

粒子群优化(Particle Swarm Optimization, PSO)算法具有容易实现、算法简单、参数较少且能有效解决全局优化问题等优点[12]．粒子群算法的速度和位置更新公式为:

(11)

(12)

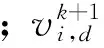
1.3 PSO-GP联合算法

本文将GP模型作为PSO算法的适应度函数,每次迭代中更新粒子的位置和速度信息,直到达到最大迭代次数时算法停止．算法流程图如图1所示．

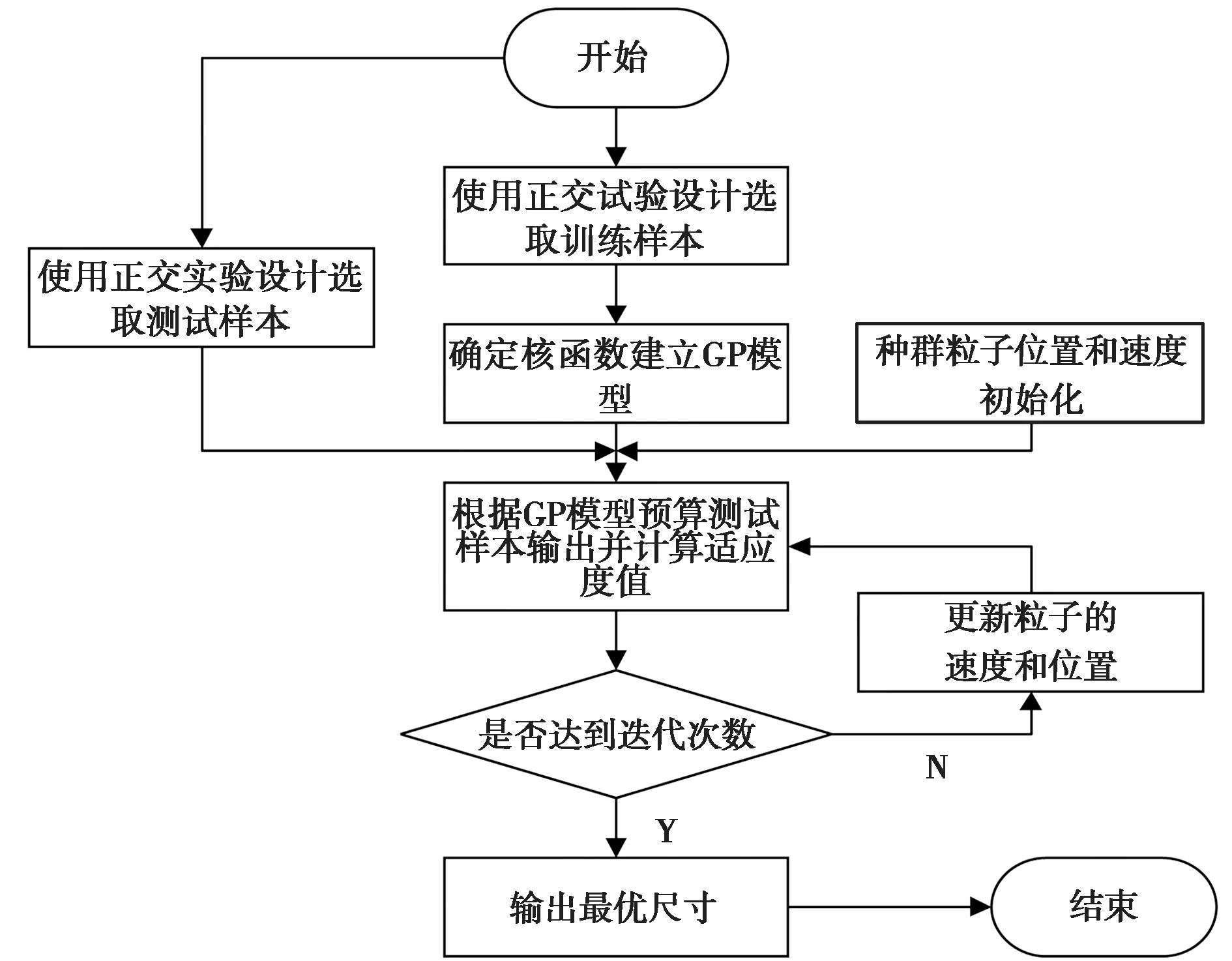
图1 粒子群-高斯过程联合算法流程图

2 GPS北斗双模微带天线

近年来,GPS微带天线广泛应用在各类移动终端上[13]．本文研究了一种GPS北斗双模微带天线,可以应用于GPSL1和北斗B1频段,如图2所示．该天线是一种方形圆极化微带天线,底层采用圆形接地板,接地板上方为正方形的介质基板．介质基板材料为相对介电常数εr=4.5的Arlon AD450．介质板上方覆盖正方形的辐射贴片,贴片四边为宽度相同、长度不同的两种枝节．该天线采用偏心馈电方式．

GPS北斗双模微带天线的设计指标要求在1.561 GHz(北斗B1工作频率)和1.575 GHz(GPSL1工作频率)处的电压驻波比小于等于1.5．本文通过优化辐射贴片边长W、低频模态枝节长度L1、高频模态枝节长度L2的尺寸来达到设计指标,这三个参数的取值范围如表1所示,其他尺寸参数如表2所示．

HFSS是一款全波三维电磁仿真软件,能计算任意形状的三维无源结构的S参数和全波电磁场．HFSS凭借其极高的仿真精度,在射频、微波、天线、高速电路等领域得到广泛的应用．本文使用HFSS计算GPS北斗双模微带天线性能指标作为GP模型的训练数据,GPS北斗双模微带天线的HFSS模型如图3所示．

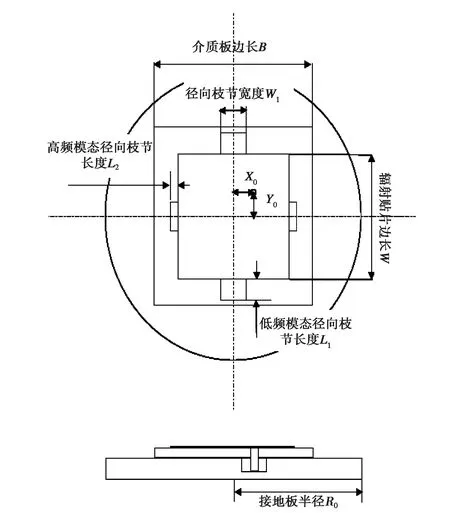
图2 GPS北斗双模微带天线结构图

结构名称 尺寸参数/mm 变量值/mm正方形辐射贴片边长W42～45径向枝节低频模态长度L1高频模态长度L25.1～6.33～3.9

表2 GPS北斗双模微带天线固定尺寸参数

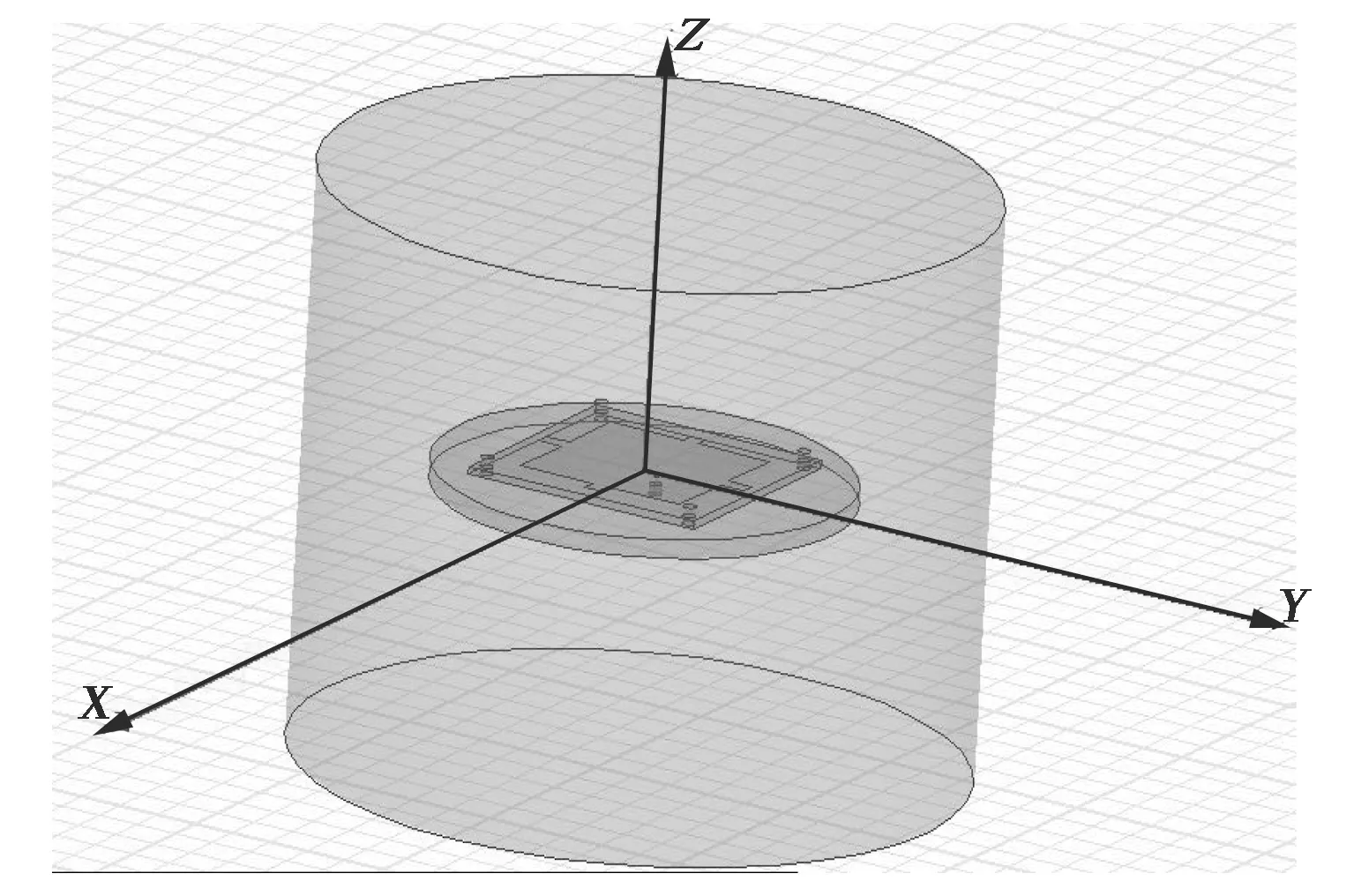
图3 GPS北斗双模微带天线的HFSS模型

3 基于高斯过程模型的GPS北斗双模天线优化设计

根据部分组合正交实验设计方法,选取24组(W,L1,L2)数据作为GP模型的训练样本,将这些数据带入HFSS进行仿真,得到S11参数值,作为GP模型的训练输出数据,从而建立起GP模型．另外选取24组(W,L1,L2)数据作为GP模型的测试样本．实验过程中PC机处理器为Intel(R) Core(TM) i5-6500@3.2 GHz、RAM为4 GB,选取ARD Matern 5/2函数为GP模型核函数．GP模型输出的S11参数值表示为ypred,i,HFSS仿真得到的对应S11参数值表示为ytest,i．为了对该双模微带天线的频率特性有全面了解,实验过程中取频率范围为1.2～1.8 GHz,GP模型建立过程中,每组数据选取251个频率点．GP模型采用如下均方误差公式进行评价:

(13)

评价结果如表3所示．

GPS北斗双模微带天线的GP模型建好后,采用PSO算法进行优化设计,PSO算法中粒子数为24,最大迭代次数为2 000,加速常数c1=c2=2,惯性权重ω=1,粒子最大速度vmax=(0.75, 0.3, 0.225),优化结果为(W，L1，L2)=(43.107 2，5.532 2，3.259) mm,建立高斯过程模型以及优化的总时间为6 611.69 s,其中建立高斯过程模型的时间为33.99 s．如果采用PSO与HFSS联合优化的方法,每调用一次HFSS需耗时约67 s,每一代24个粒子(24组尺寸)需耗时1 608 s,2 000次迭代需耗时大约3 216 000 s,远远超过使用高斯过程模型作为粒子群算法适应度函数所需要的时间．HFSS仿真得到的S11参数如图4所示．从图4可以看出,在1.561 GHz和1.575 GHz两点处S11分别为-23.169 8 dB和-18.799 8 dB,满足电压驻波比小于1.5的设计要求．

最优尺寸下GP模型的S11预测值ypred和HFSS仿真得到的S11值yHFSS的对比如图5所示,可以看出两者吻合程度很好,说明GP模型足够精确．

GPS北斗微带天线的设计中,在考虑频率特性的同时,一般也需要考虑极化特性．这里通过在上述最优尺寸下观察天线在1.561 GHz以及1.575 GHz处的轴比来判断天线的极化特性,如图6所示．从图6可以看出,在1.561 GHz和1.575 GHz处天线的轴比分别为0.843 2 dB和1.564 1 dB,因此可以判断该天线是圆极化天线．

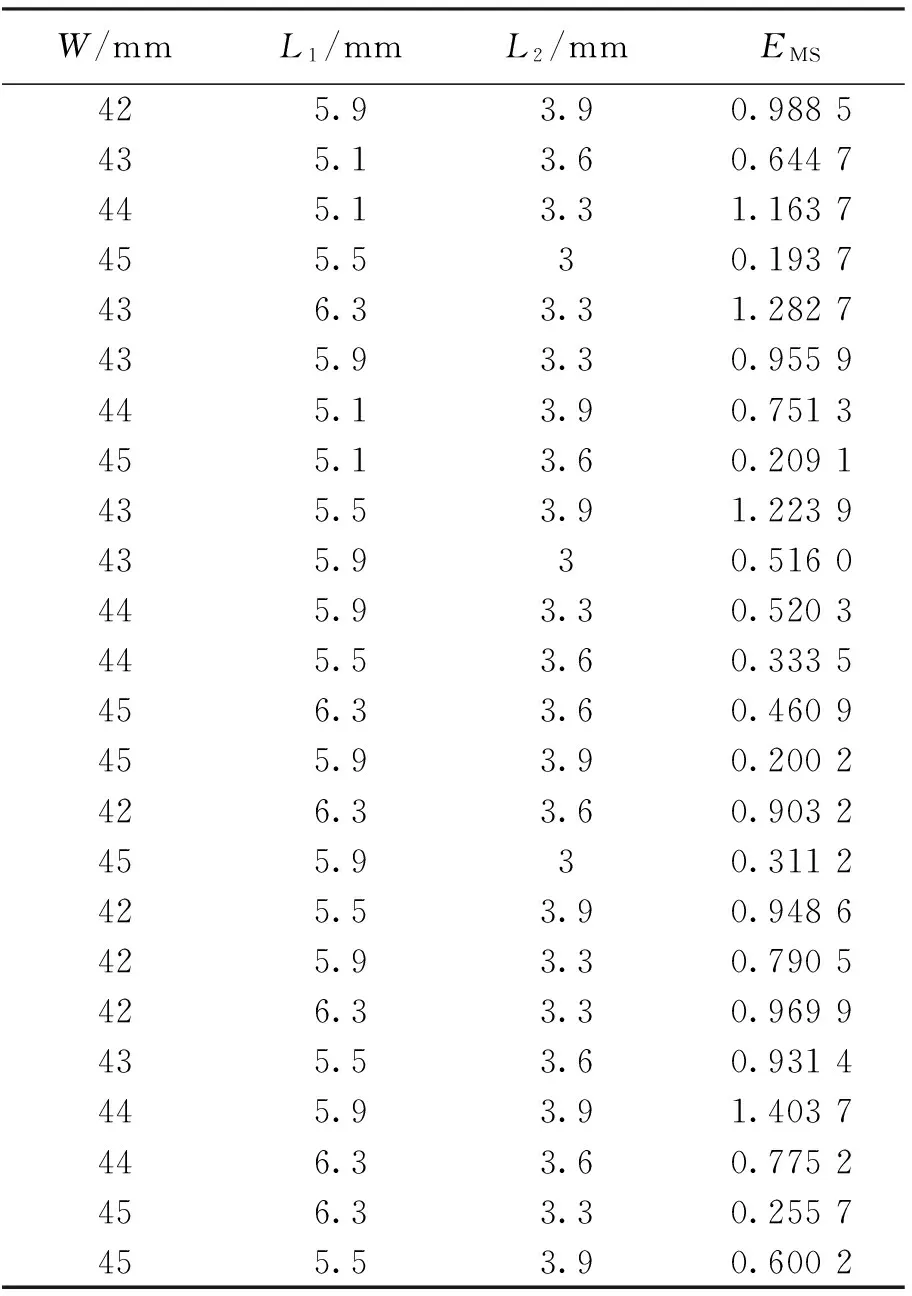
表3 高斯过程预测均方误差

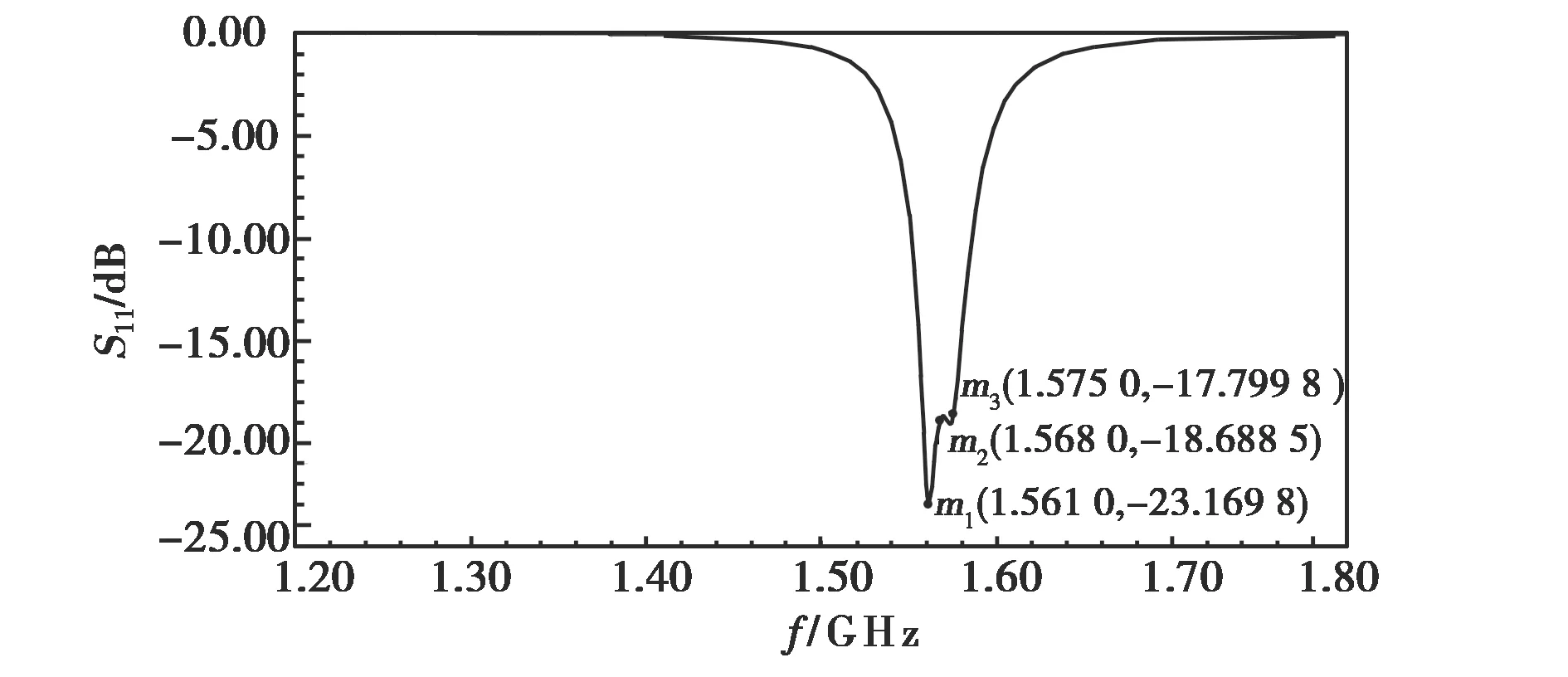
图4 S11仿真结果

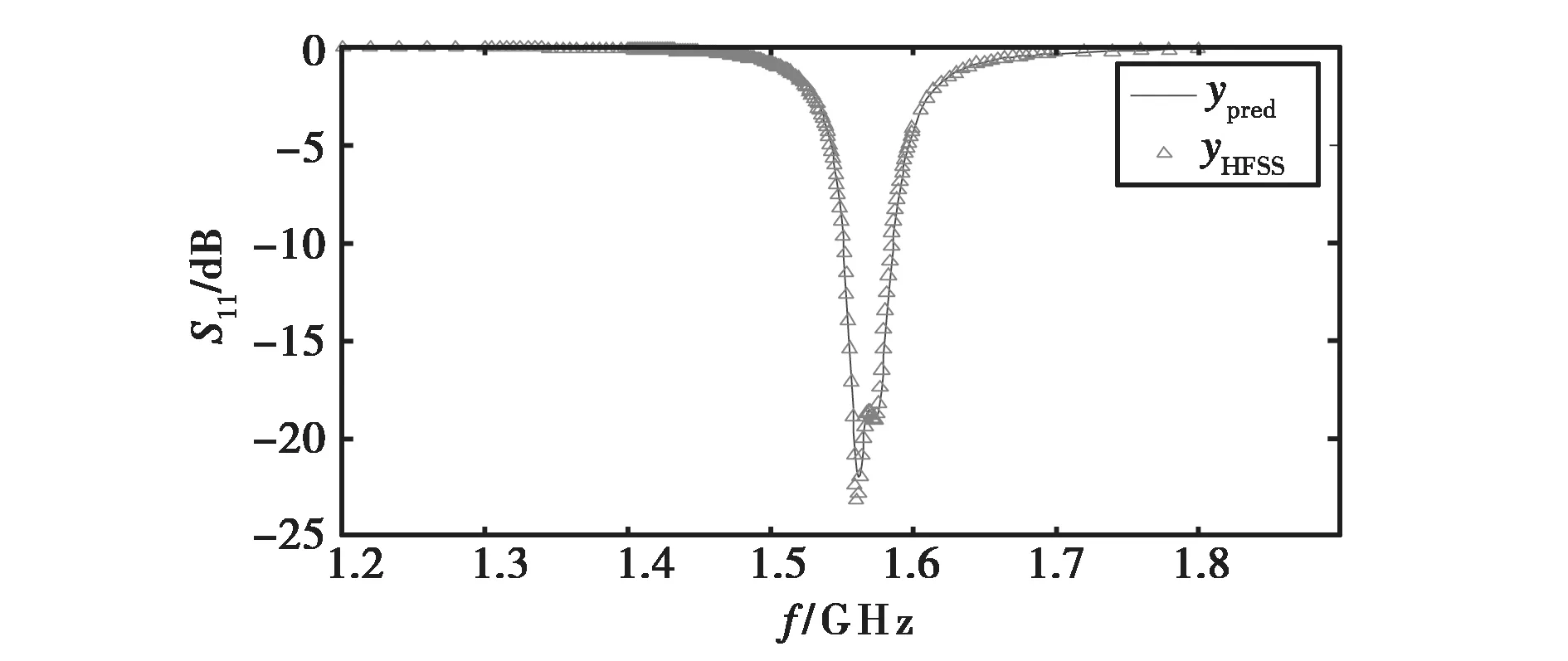
图5 GP模型预测值与HFSS仿真值的比较

图7,8给出了双模微带天线在工作频率点的增益方向图,从这两张图可以看出,天线在1.561 GHz和1.575 GHz处总增益最大值分别为5.349 dB和5.403 1 dB,在-110°～110°范围内,天线主要表现为右旋圆极化特性．

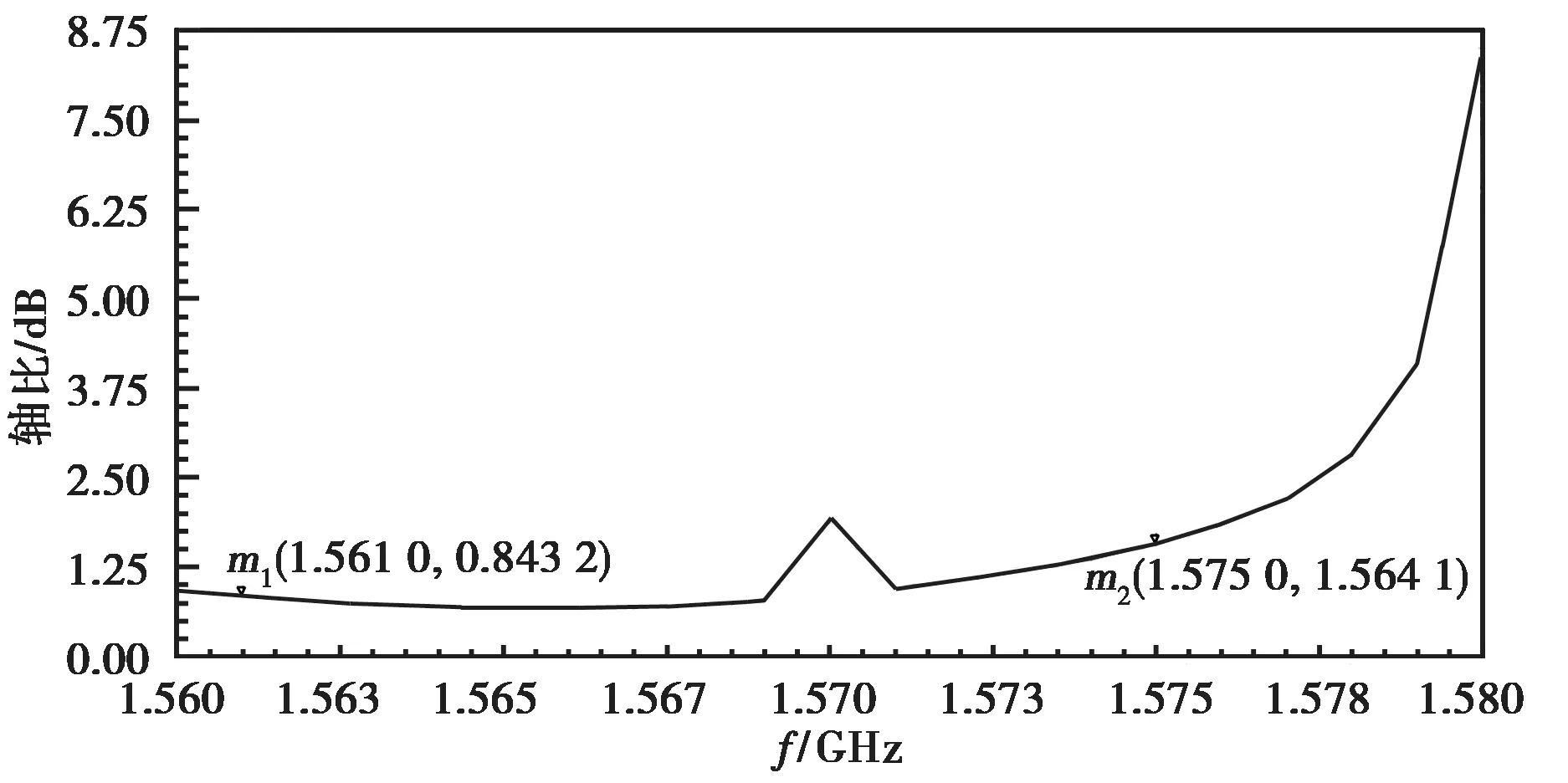
图6 轴比仿真结果

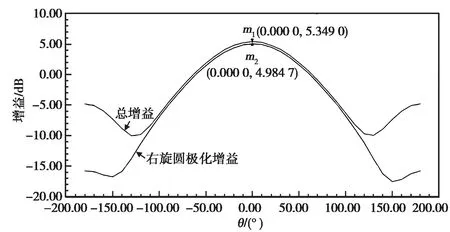
图7 1.561 GHz处天线增益方向图

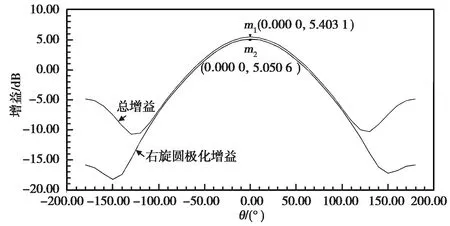
图8 1.575 GHz处天线增益方向图

4 结 论

本文将高斯过程模型作为粒子群算法的适应度函数,有效减少了以往天线优化设计中调用电磁仿真软件HFSS的次数,从而大幅减少寻找最优解的时间．构建的高斯过程模型的预测输出值接近HFSS精确仿真结果,表明该建模方法有足够的可靠性,优化设计得到的GPS北斗双模微带天线尺寸满足设计要求,说明该方法在本文的天线优化设计中具有实际利用价值．

[1]CHEN M, CHEN C C.A compact dual-band GPS antenna design[J].IEEE transactions on antennas and propagation, 2013, 12(3)：245-248.

[2]SUN C, ZHENG H L, LIU Y.Analysis and design of a low-cost dual-band compact circularly polarized antenna for GPS application[J].IEEE transactions on antennas and propagation, 2016, 64(1)：365-370.

[3]CHEN H M, LIN Y F, CHEN C H, et al.Miniature folded patch GPS antenna for vehicle communication devices[J].IEEE transactions on antennas and propagation, 2015, 63(5)：1891-1898.

[4]AFSHINMANESH F, MARANDI A, SHAHABADI M.Design of a single-feed dual-band dual-polarized printed microstrip antenna using a boolean particle swarm optimization[J].IEEE transactions on antennas and propagation, 2008, 56(7)：1845-1852.

[5]KIBRIA S, ISLAM M, YATIM B, et al.A modified PSO technique using heterogeneous boundary conditions for broadband compact microstrip antenna designing[J].Annals of telecommunications, 2014, 69(9)：509-514.

[6]RASMUSSEN C, WILLIAMS C.Gaussian processes for machine learning[M].Cambridge：MIT Press, 2006：7-32.

[7]何志昆, 刘光斌, 赵曦晶, 等.高斯过程回归方法综述[J].控制与决策, 2013, 28(8)：1121-1129.

HE Z K, LIU G B, ZHAO X J, et al.Overview of Gaussian process regression[J].Control and decision, 2013, 28(8)：1121-1129.(in Chinese)

[8]张乐, 刘忠, 张建强, 等.一种改进高斯过程的回归建模方法[J].华中科技大学学报(自然科学版), 2013, 41(10)：115-118.

ZHANG L, LIU Z, ZHANG J Q, et al.Improved Gaussian process regression modeling method[J].Journal of Huazhong University of Science &Technology(natural science edition), 2013, 41(10)：115-118.(in Chinese)

[9]VILLIERS D, JACOBS J.Gaussian process modeling of CPW-fed slot antennas[J].Progress in electromagnetics research, 2009, 98(5)：233-249.

[10]JACOBS J, KOZIEL S.Two-stage framework for efficient Gaussian process modeling of antenna input characteristics[J].IEEE transactions on antennas and propagation, 2014, 62(2):706-713.

[11]LIU B, ALIAKBARIAN H, GIELEN G.An efficient method for antenna design optimization based on evolutionary computation and machine learning techniques[J].IEEE transactions on antennas and propagation, 2014, 62(1):7-18.

[12]田雨波.粒子群优化算法及电磁应用[M].北京：科学出版社, 2014：179-244.

[13]徐兴福.HFSS射频仿真设计实例大全[M].北京：电子工业出版社, 2015：415-447.

强哲 (1992-),男,江苏人,硕士研究生,研究方向为智能信息处理与系统．

陈艺 (1992-),女,江苏人,硕士研究生,研究方向为智能信息处理与系统．

田雨波 (1971-),男(满族),辽宁人,教授,博士,硕士生导师,2009年到美国UCLA做访问学者．主要研究方向为计算智能及其电磁学应用．

许兰 (1992-),女,安徽人,硕士研究生,研究方向为智能信息处理与系统．

Optimization of GPS antenna by PSO-based GP modeling

QIANG Zhe CHEN Yi TIAN Yubo XU Lan

(SchoolofElectronicsandInformation,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China)

Now, the optimization algorithm with electromagnetic simulation software HFSS are often combined to design the microstrip antennas.However, a large number of accurate electromagnetic simulations are very time-consuming and need high performance computer.In order to solve the problem, a method, which replaces full-wave electromagnetic simulation with Gaussian process modeling and then optimizes with the particle swarm optimization(PSO) algorithm, is proposed.The method can reduce the time to 0.2% of the previous method.The method is used to optimize the GPS dual-mode microstrip slot antenna(MSA).The optimal results of GPS dual-mode MSA satisfy the design demands which proves the effectiveness of the method.

Gaussian process;PSO;GPS antenna;HFSS

强哲, 陈艺, 田雨波, 等.基于粒子群算法的高斯过程建模对GPS天线优化设计研究[J].电波科学学报,2016,31(5):927-932.

10.13443/j.cjors.2016052201

QIANG Z, CHEN Y, TIAN Y B, et al.Optimization of GPS antenna by PSO-based GP modeling[J].Chinese journal of radio science,2016,31(5):927-932.(in Chinese).DOI：10.13443/j.cjors.2016052201

2016-05-22

国家自然科学基金(61401182)

TN82

A

1005-0388(2016)05-0927-06

联系人：强哲 E-mail：qiangzhemail@gmail.com