雷达关联成像中的阵元位置误差分析

徐先武，程永强，秦玉亮，周小利

(国防科技大学 电子科学与工程学院, 长沙 410073)



·信号处理·

雷达关联成像中的阵元位置误差分析

徐先武，程永强，秦玉亮，周小利

(国防科技大学 电子科学与工程学院, 长沙 410073)

雷达关联成像是一种全新的凝视高分辨成像方法，在军事上有着广阔的应用前景。文中针对阵列雷达普遍存在的阵元位置误差问题，建立了存在阵元位置误差下的雷达关联成像模型，得到了泰勒展开下目标回波与阵元位置误差的线性关系；推导了存在阵元位置误差条件下雷达关联成像的理论误差限，准确预测了阵元个数、信号带宽、成像单元尺寸和数目、目标散射系数和散射中心数目对成像误差的影响。研究结果为雷达关联成像系统参数的设置以及阵元位置误差补偿提供了一定的参考和依据。

阵列雷达；雷达关联成像；阵元位置误差；克拉美罗下界

0 引 言

成像雷达具备全天候、全天时、远距离观测的能力，在军用领域的战场侦察、目标识别和精确打击以及民用领域的天体测绘、地形测绘和海洋观测等应用中具有重要意义。经过多年研究，成像雷达在系统结构、成像方法和应用场景等方面得到很大的发展。目前，合成孔径雷达和逆合成孔径雷达在高分辨成像方面发展相对成熟[1]。然而，这些成像雷达大多基于距离-多普勒原理，其距离向分辨率取决于带宽，方位向分辨率依赖于多普勒，在凝视/近凝视的非理想观测几何条件下以及非合作目标等情况下成像性能急剧恶化。

雷达关联成像采用新的成像思路，通过阵列天线产生在时间和空间上随机分布的二维随机辐射场，依靠雷达信号本身的差异性实现对目标的高分辨成像。其方位向分辨率不再依赖于雷达与目标的相对运动，而是与辐射场的差异性有关，即辐射场中相邻两点信号的差异性决定了这两点的分辨[2-4]。最终通过回波信号与辐射场参考信号的相关处理就能得到目标信息，如果结合稀疏重构理论以及各类参数化方法，则能得到更高分辨率的图像。

雷达关联成像模型要求准确已知的辐射场参考信号，这就意味着各阵元的相对位置要准确已知，但是在实际情况下，存在安装误差、测量误差以及由阵列工作环境改变、工作平台振动等引起的误差[5]，这些误差导致阵元位置存在偏差，影响延时信号推算的准确性，造成辐射场参考信号与实际回波信号失配，进而影响目标重构的效果。实际上，阵元位置误差广泛存在于阵列雷达中，对阵列雷达的性能都有较大影响[6-7]。

本文在阵列雷达普遍存在阵元位置误差的背景下，以雷达关联成像为基础，着重分析阵元位置误差对雷达关联成像的影响。首先，简要介绍雷达关联成像基本原理；然后，在考虑阵元位置误差情况下，建立雷达关联成像线性模型以及推导目标散射系数估计的克拉美罗下界(CRLB)；最后，仿真分析带宽等因素对成像误差的影响及其原因，验证理论分析的正确性。

1 雷达关联成像原理

雷达关联成像是从量子成像引入的一个概念，文献[4]详细介绍了雷达关联成像的基本原理，建立了雷达关联成像的数学模型并设计了相应成像算法。雷达关联成像是通过雷达阵列发射一组时间不相关、且相互正交的信号，在成像区域形成具有时间-空间不相关的辐射场，并且根据已知发射波形和成像几何关系推演辐射场参考信号，最终通过接收信号与辐射场参考信号的关联处理实现目标信息的解耦，获得目标的散射强度以及其空间分布[4]。其基本原理如图1所示。

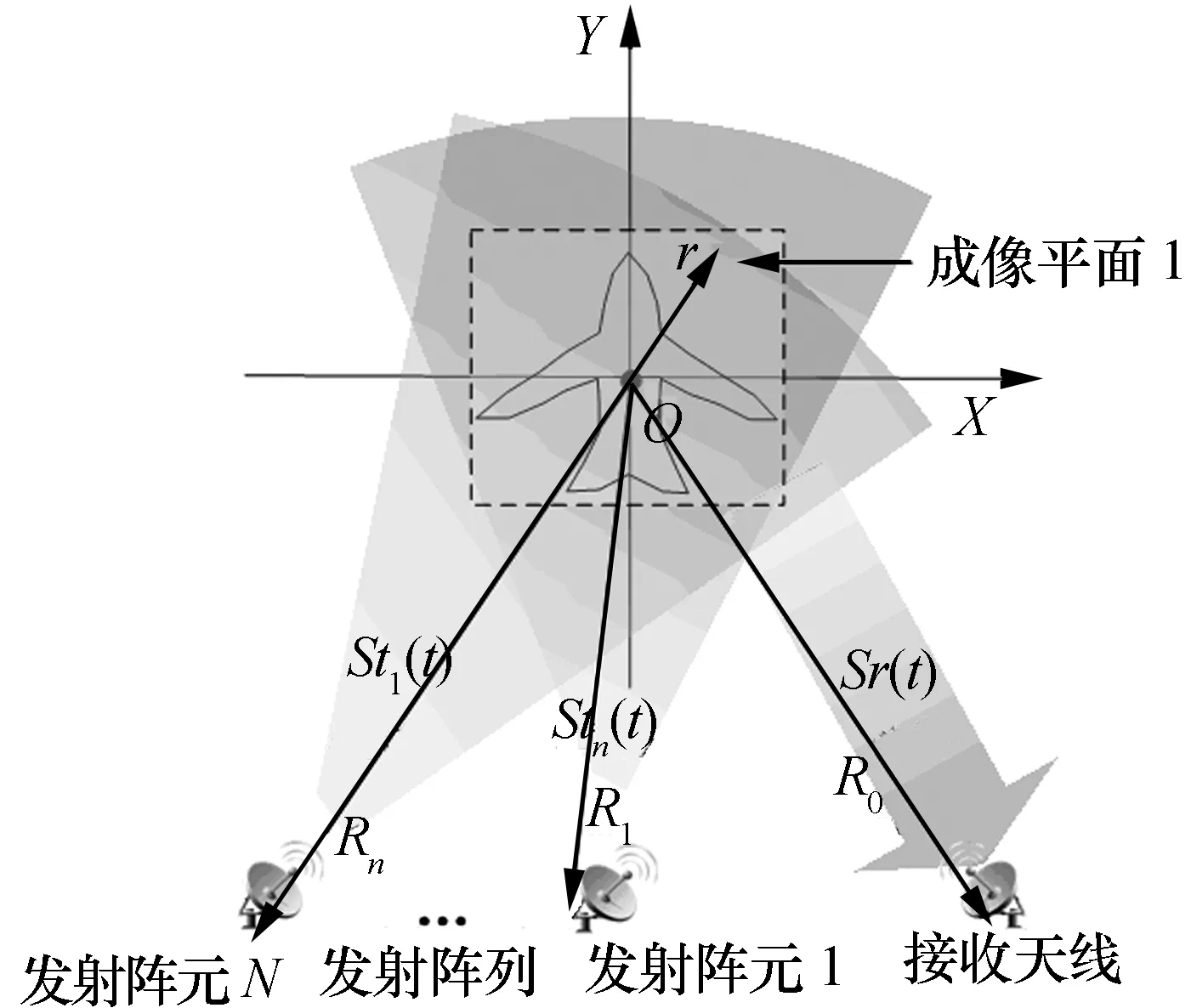
图1 雷达关联成像示意图

图1中雷达关联成像采用N个发射阵元，1个接收阵元，接收信号表示为Sr(t)，第n个发射阵元的信号表示为Stn(t)，则发射信号矢量为St(t)=[St1(t),St2(t), …,StN(t)]，其中n∈{1,2,…,N}。以成像平面中心建立直角坐标系，r是成像区域内某点的位置矢量，Rn是第n个发射阵元的位置矢量，R0是接收阵元的位置矢量。假定各发射信号满足相互正交性和时间不相关性，即其自相关函数为

δ(t1-t2)·δ(m-n)

(1)

如考虑到各阵元信号到成像区域的延时，可将成像平面中r位置处的辐射信号表示为

(2)

式中：c表示光的传播速度。由文献[4]可知辐射场信号的自相关函数为

Nδ(r-r′;τ-τ′)

(3)

式中：r′和r表示两个不同的位置矢量，τ和τ′表示两个不同的延时。综上可得：多个阵元发射时间不相关且相互正交的信号，可在成像区域形成空间-时间不相关的随机辐射场。

若考虑成像区域到接收阵元的时延，可将接收回波信号表示为

Sr(t)=∫Iσr·S(r,t)dr

(4)

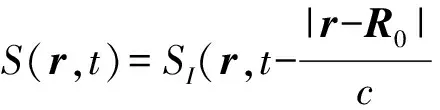
把回波信号Sr(t)与r′处的辐射场参考信号S(r′,t)做关联处理(称为相关法)，可得

(5)

根据信号形式、阵列构型等系统设置可灵活的求出成像平面中任意一点的辐射场参考信号，再依据式(5)把回波信号与辐射场参考信号做关联处理，就可以精确获得成像区域的目标散射信息，从而重构目标图像。

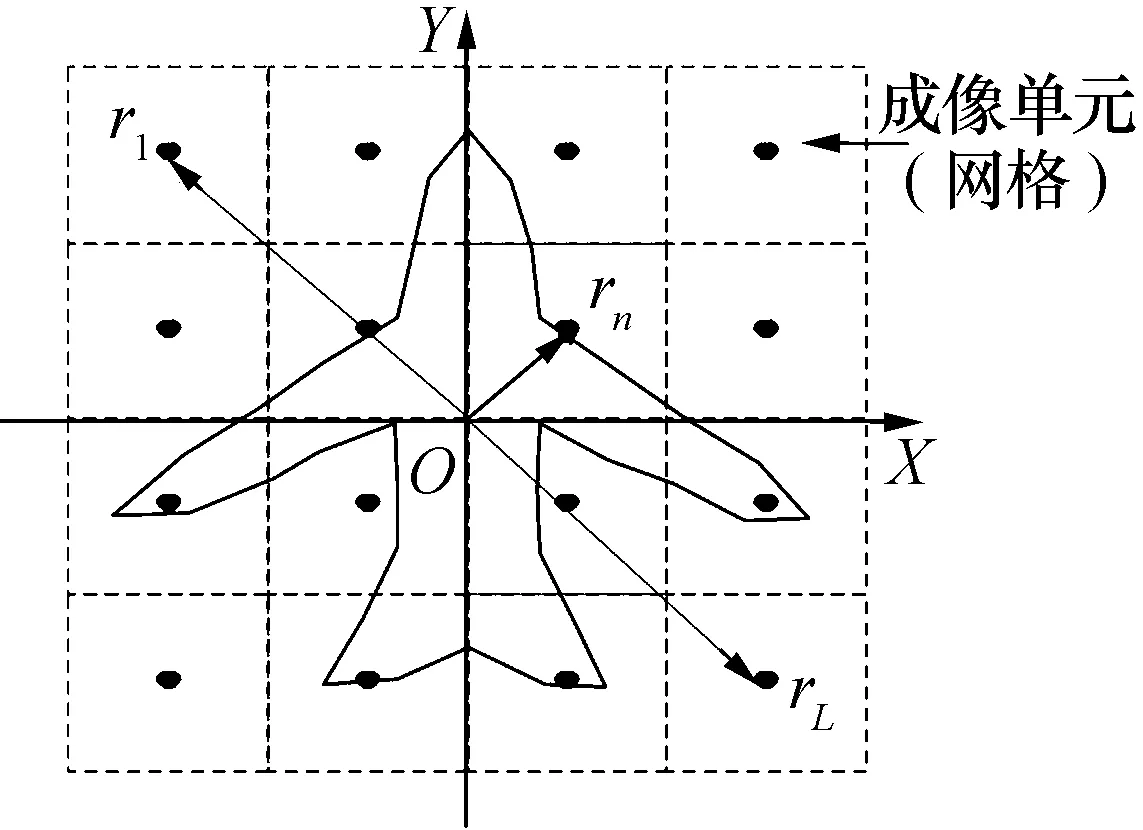
图2 成像区域单元化

将时间离散化，得t=[t1,t2,…,tM]T；对成像平面进行成像单元划分(如图2所示)，得[r1,r2,…,rL]。代入式(4)得

(6)

因此，雷达关联成像的数学模型可表示为

Sr=S·σ

(7)

式中：Sr表示回波矢量；S表示辐射场参考信号矩阵；σ表示目标散射系数矢量。

由于辐射场信号具有时间-空间不相关性，而回波信号是各散射点处的辐射场信号的线性叠加，所以rank(S)=rank(S,Sr)=rank(Sz)=min(M,L),其中Sz=(S,Sr)表示S的增广矩阵。由线性代数理论中可知，如果min(K,L)=L，即时间采样点个数不少于成像单元的个数，此方程有唯一解σ=S-1·Sr(称为伪逆法)。

2 存在阵元位置误差下的雷达关联成像模型

为了研究阵元位置误差对雷达关联成像的影响，本节首先在二维平面内建立如图3所示的模型，以接收阵元为原点建立直角坐标系。实心圆代表实际的阵元位置，空心圆代表理论阵元位置，即测量所得阵元位置；(xn,yn)表示第n个阵元的坐标，n∈{0,1,…,N}；(xcl,ycl)表示第l个成像单元的坐标，l∈{0,1,…,L}；且令第n个发射阵元的位置误差矢量为ΔPn=(Δxn,Δyn)，接收阵元的位置误差矢量为ΔP0=(Δx0,Δy0)。

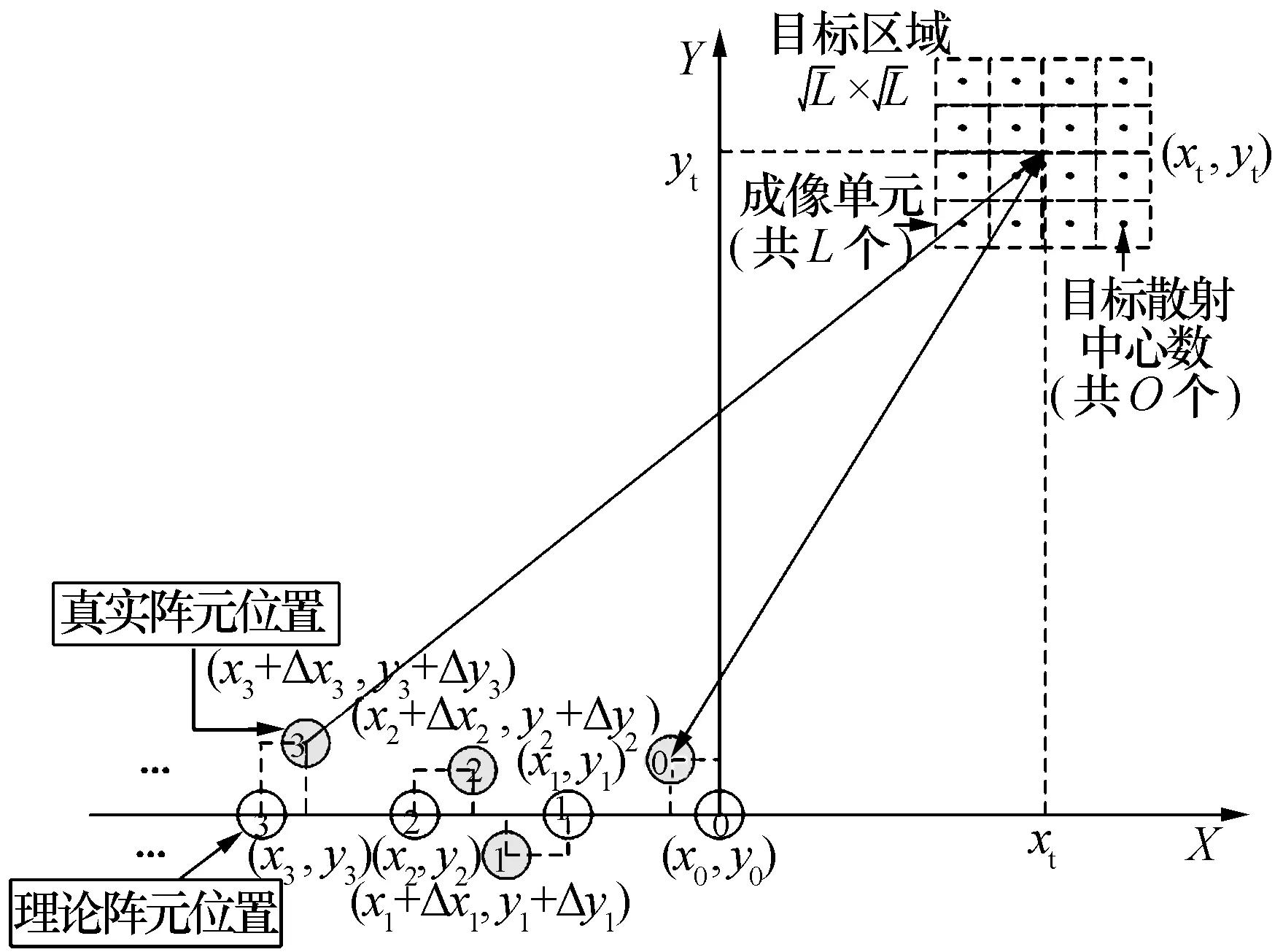
图3 存在阵元位置误差的成像模型

设发射信号为

Stn(t)=Anexp[j·(2πfn(t)·t+φn)]

(8)

式中：下标n表示第n个发射阵元；A表示振幅；f(t)表示随采样时间跳变的频率；φ表示初始相位。

定义S(tm,cl)表示tm时刻第l个成像单元对应的辐射场参考信号，则有

(9)

式中：m∈{1,2,…,M}，M表示样本数；τnl表示发射阵元n到成像单元l再到接收阵元的时延

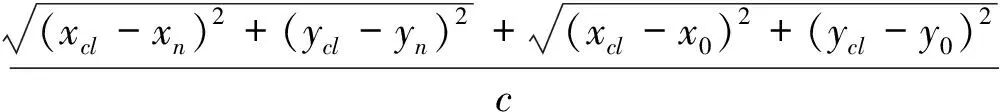
(10)

因此，可得理论回波为

Sr(tm)= [S(tm,c1), S(tm,c2), …, S(tm,cL)]·

[σ1,σ2,…,σL]T

(11)

(12)

式(12)由一阶泰勒公式在τnl处展开且去除高阶项得

(13)

式中：Δτnl表示时延误差，具体如式(14)所示

(14)

此时，实际辐射场参考信号为

(15)

式(15)可用一元一阶泰勒公式在S(tm,cl)处进行展开，去除高阶项得

(16)

式中：ΔS(tm,cl)表示辐射场误差，具体如式(17)所示

(17)

综合可得，实际回波信号为

Sr(tm)+ΔSr(tm)

(18)

式中：ΔSr(tm)表示回波误差，具体如式(19)所示

Q(tm)·Δx0+P(tm)·Δy0

(19)

其中

(20)

(21)

(22)

(23)

(24)

因此，可将存在阵元位置误差下的雷达关联成像方程写为

(25)

3 雷达关联成像的理论误差限

参数估计的CRLB 是无偏估计量方差的下界，也是描述参数估计极限性能的一个指标[8]。本节将阵元位置误差当作随机变量，推导目标散射系数估计的CRLB。首先，假设阵元位置误差服从高斯分布，设其均值为0，方差为η2，即

Δxn～N(0,η2), Δyn～N(0,η2)

n∈(0,1,…,N)

(26)

由概率论可知若干高斯分布经过线性运算后同样服从高斯分布，因此可得实际回波信号也同样服从高斯分布，令μ(σ)表示其均值向量，C(σ)表示其协方差矩阵，即得

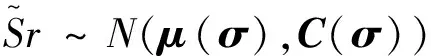
(27)

根据高斯情况下的CRLB理论可得[8]

(28)

进一步分析，显然有

μ(σ)=S·σ

(29)

(30)

由于不同阵元的发射信号是相互正交的，跳频信号的每一个频点都有一个持续时间，且成像距离一般远大于成像区域，因此式(30)中的均值部分可进一步近似并化简为式(31)所示

(31)

现采用带宽为B、载频为fc的随机跳频信号，则其自相关函数为

综上可得，协方差矩阵为

(32)

因此，将式(28)和式(32)代入式(27)中的第一项可得

(33)

同理，代入第二项为

(34)

综合式(33)和式(34)可得Fisher信息矩阵为

[I(σ)]ij=

(35)

将Fisher矩阵求逆取对角元素，就可得到阵元位置误差下各散射系数估计的CRLB，即理论误差限。初步分析可得，阵元位置误差对成像的影响与很多因素有关，包括：阵元位置误差的大小(η)、阵元数目(N)、成像单元数目(L)、目标散射系数和散射中心数目(σ)、信号载频和带宽(fc,B)、样本数(M)以及与延时(τ)有关的成像单元尺寸、阵元位置间距、目标距离等。

4 仿真分析

鉴于Fisher矩阵比较复杂而无法直接求逆，本节采用数值仿真的方法求CRLB，并对比同等条件下模拟实验的目标重构方差，分析系统各个参数与阵元位置误差对雷达关联成像的影响。

4.1 参数和场景设置

表1 基本参数设置

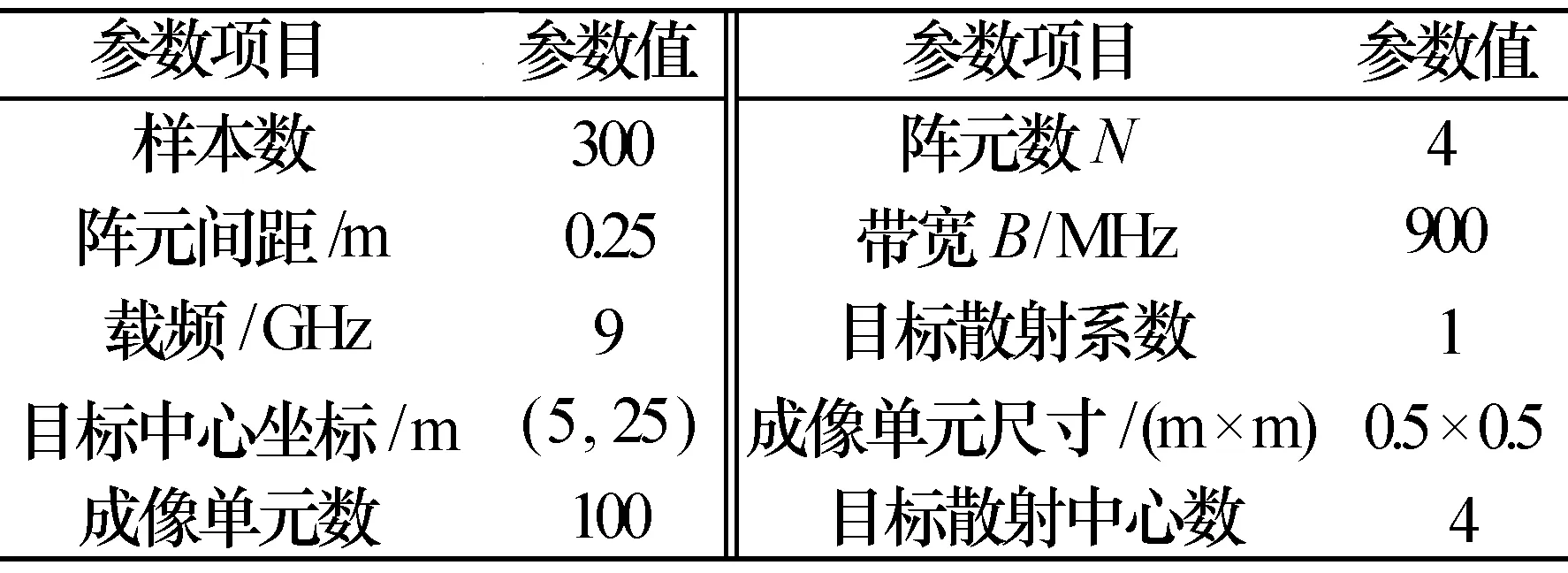
另外，在[0, 0.001] (m)范围内，设置步长为0.000 1(m)，依次取11个不同的位置误差均方差值，产生零均值高斯分布的阵元位置误差进行仿真。CRLB仿真和系统仿真都以图3作为基本场景，图4作为原始目标。

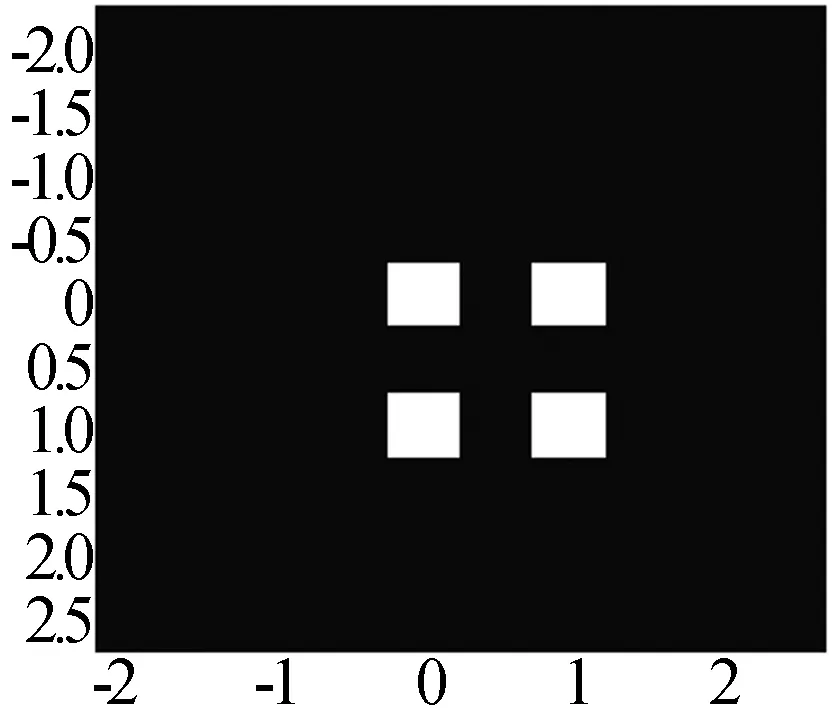
图4 原始目标图像

由于仿真实验结果具有一定的随机性，所以采用500次蒙特卡罗。另外定义目标估计方差为

(36)

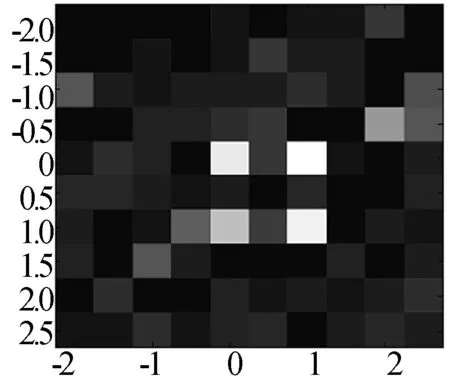
图5 阵元位置误差均方差为0.5 mm时相关法目标重构图像

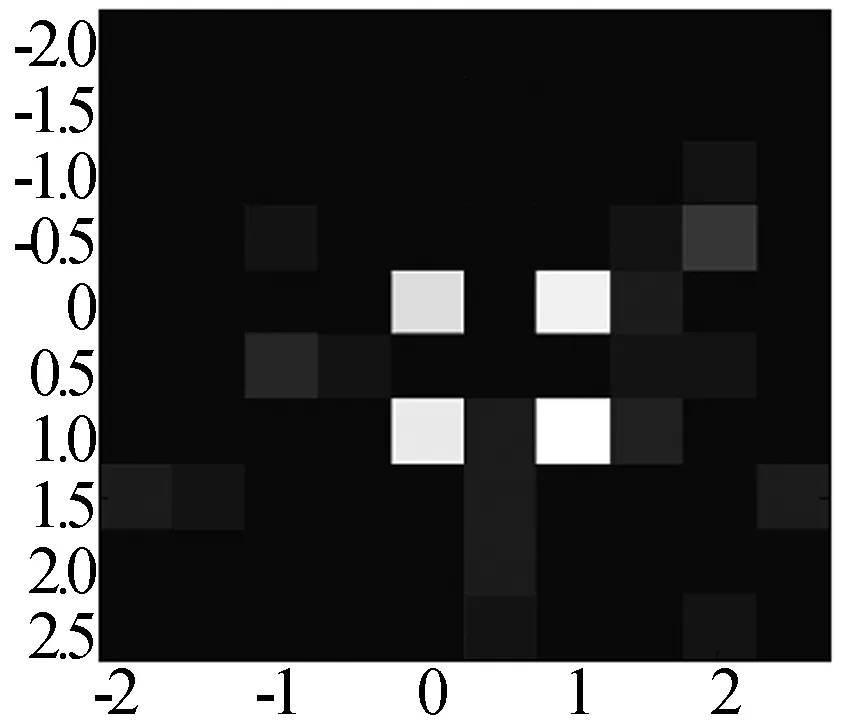
图6 阵元位置误差均方差为0.5 mm时伪逆法目标重构图像

4.2 仿真结果与分析

在以上基本参数的基础上，分别改变阵元数、带宽、成像单元尺寸、目标散射系数、目标散射中心数以及成像单元数进行仿真，得到图7～图12的实验结果。初步观察可知：(1)估计方差随着阵元位置误差的增大而增大；(2)伪逆法的方差曲线始终在CRLB曲线之上，即验证了成像理论误差限的正确性。其中，图例“CRLB# **”表示在**条件下CRLB的仿真曲线；相应的，“LS法# **”表示在**条件下伪逆法的估计方差曲线。

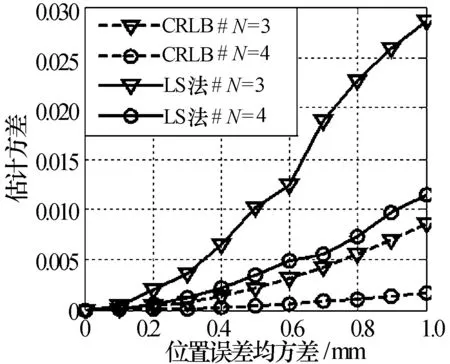
图7 不同阵元数的方差曲线

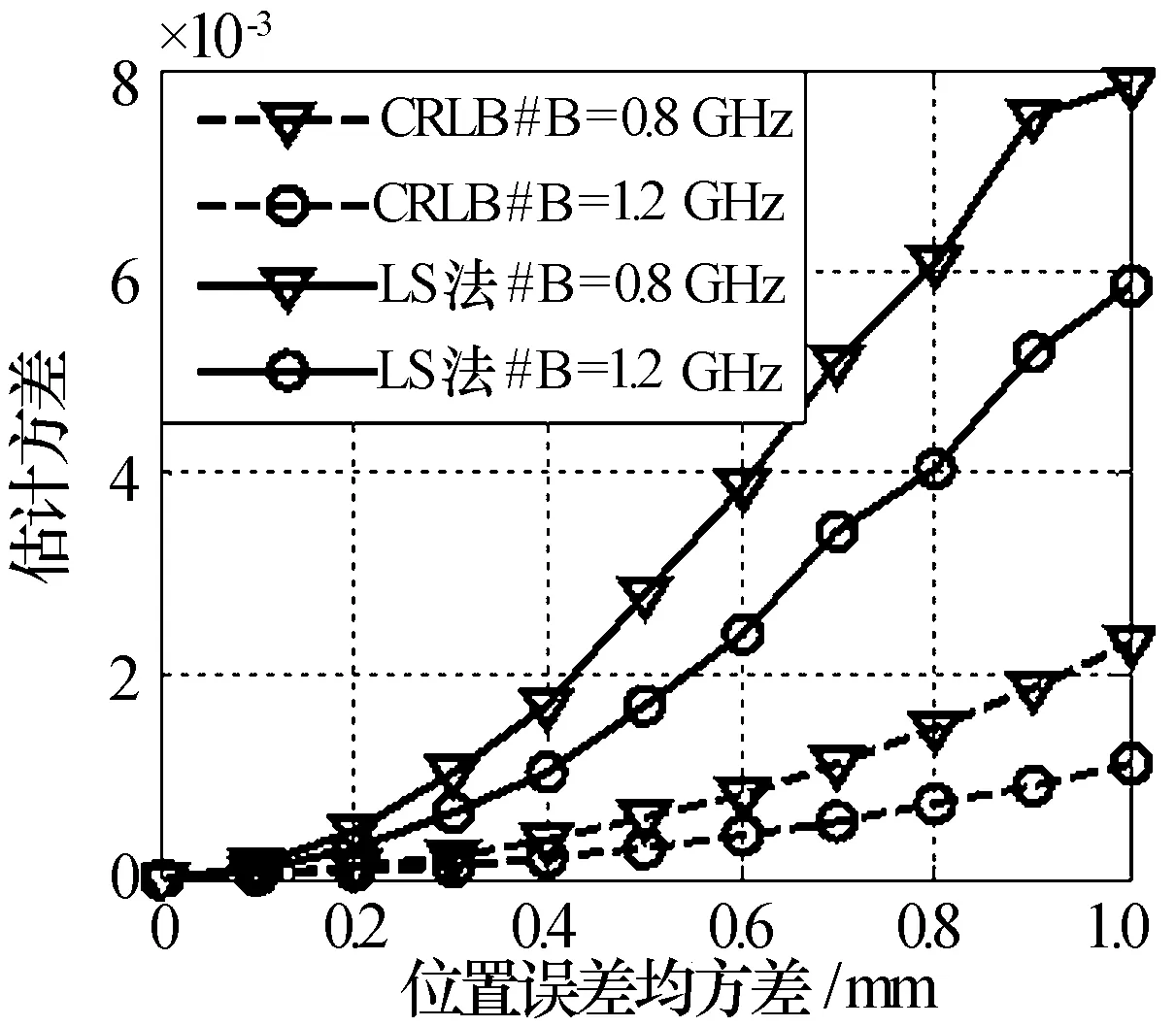
图8 不同带宽的方差曲线

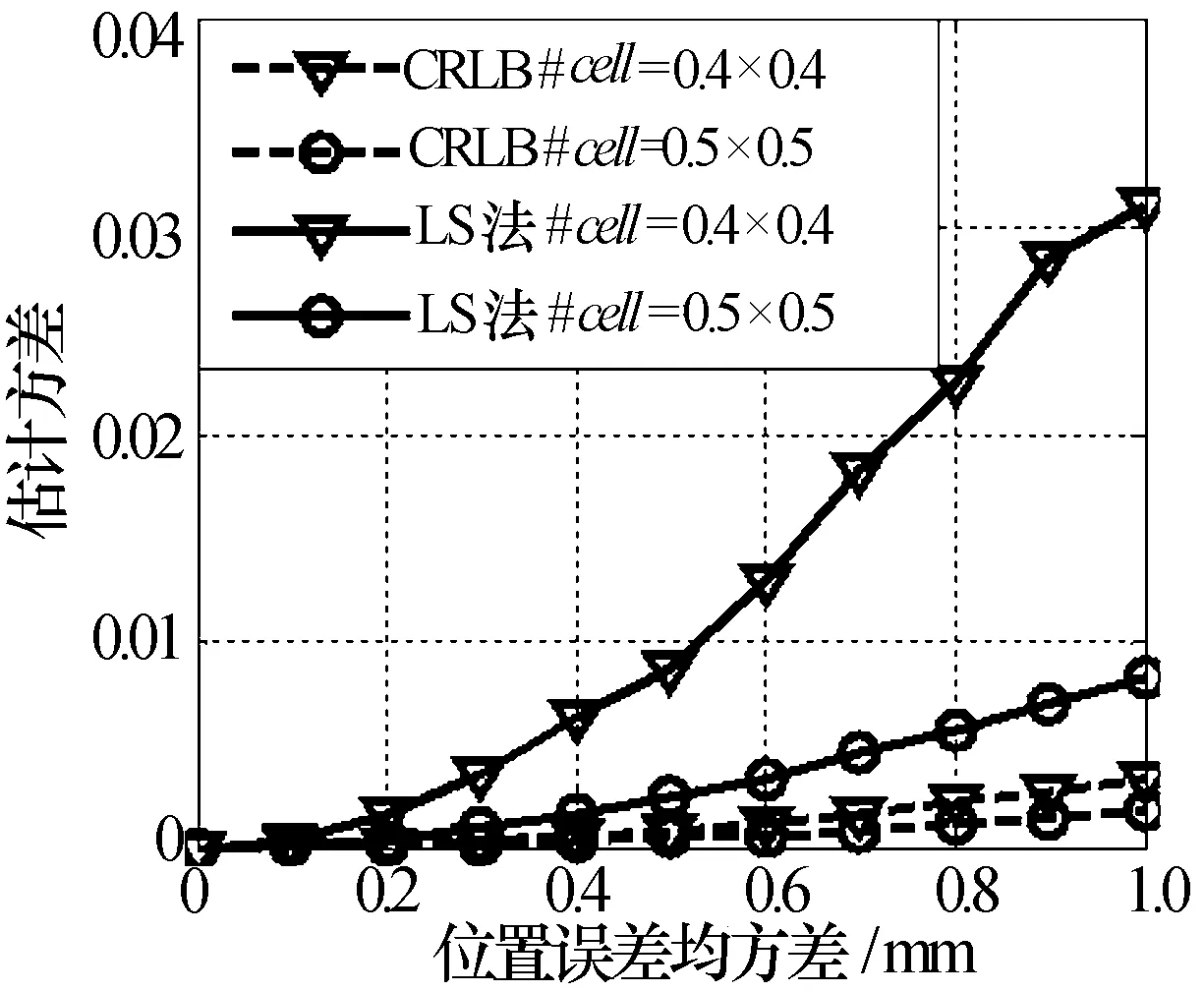
图9 不同成像单元尺寸的方差曲线

图7、图8和图9分别给出了不同阵元数、不同带宽、不同成像单元尺寸下的仿真结果。其中，阵元数分别取3和4，带宽分别取0.8 GHz和1.2 GHz，成像单元尺寸分别取0.4 m×0.4 m和0.5 m×0.5 m。由这三幅图可知，估计方差与阵元数、带宽以及成像单元尺寸成反比。因为雷达关联成像是依靠信号的差异性来分辨目标的，因此信号的不相关性对其成像质量具有很大影响。此处阵元数、带宽的增加会使整个辐射场信号更为随机，而成像单元尺寸的增大也会减弱相邻成像单元辐射场信号的相关性，进而提高了对误差的容忍度。所以在实际系统中可以适当增大阵元数、提高带宽以及增大成像单元来减少阵元位置误差对雷达关联成像系统的影响。

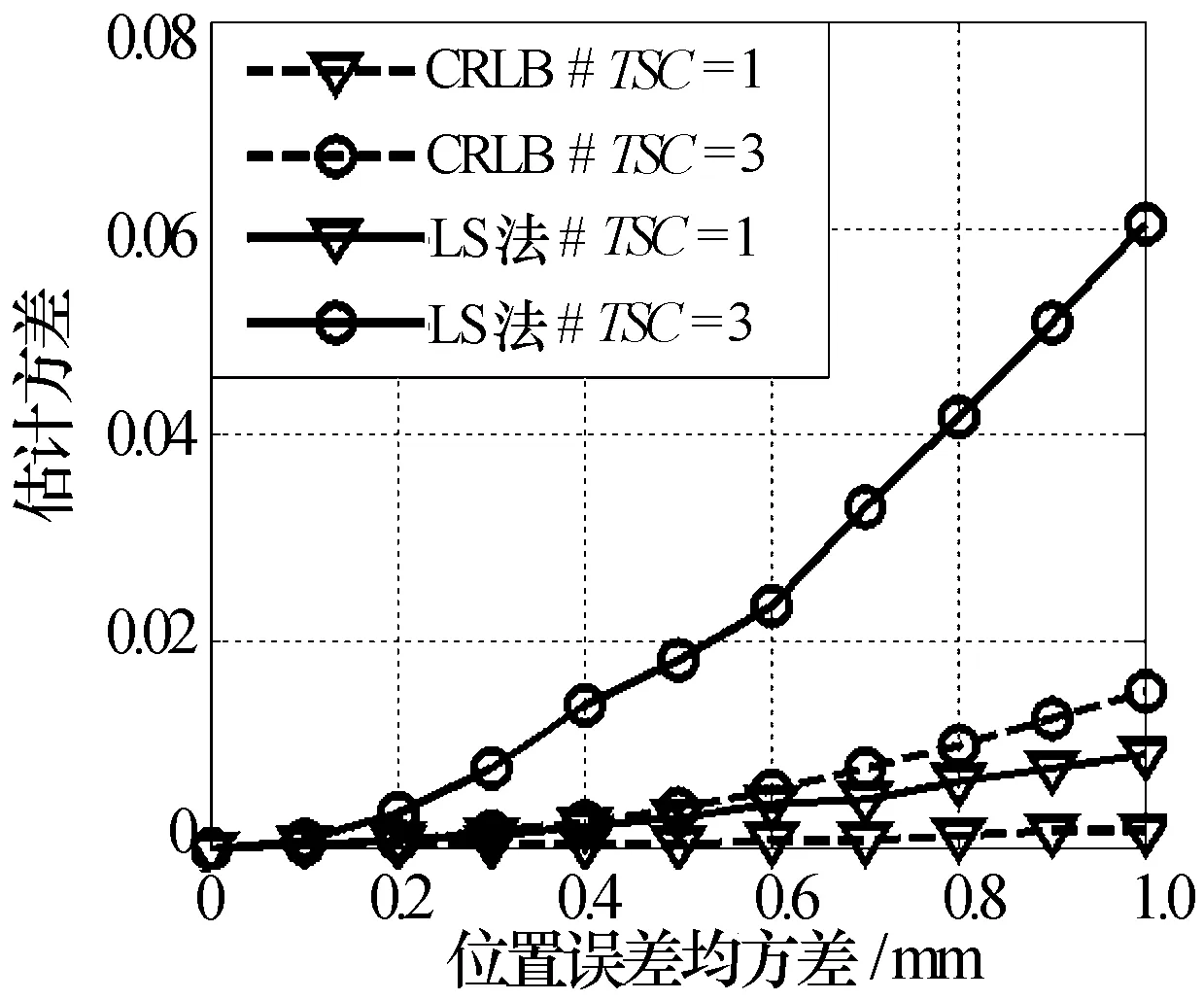
图10 不同散射系数的方差曲线

图10、图11和图12分别给出了不同目标散射系数、不同散射中心数、不同成像单元数下的仿真结果。其中，目标散射系数分别取1和3，散射中心数分别取4和8，成像单元数分别取64和144。由这三幅图可知，估计方差与目标散射系数、散射中心数以及成像单元数成正比。因为阵元位置误差直接影响信号时延，进而造成辐射场信号的推演误差，通过目标作用后，这种误差最终体现在回波信号里面。如果将实际回波与辐射场参考信号进行关联处理，这种误差会造成原本目标信号的能量泄漏，即目标信号能量散布于整个成像平面，最终重构图像中目标区域信号减弱，而其他成像区域出现虚假散射点。此处目标散射系数的增大、散射中心数的增多直接增强了回波信号的能量，提高了非目标区域的方差，而成像单元数的增多则增大了误差区域，从而提高了整体方差。此处值得指出的是，在图10中目标散射系数的增大，虽然提高了估计方差，但并没有降低其成像效果，原因在于虚假散射点与目标散射点的信号相对强度并没有实质性改变。

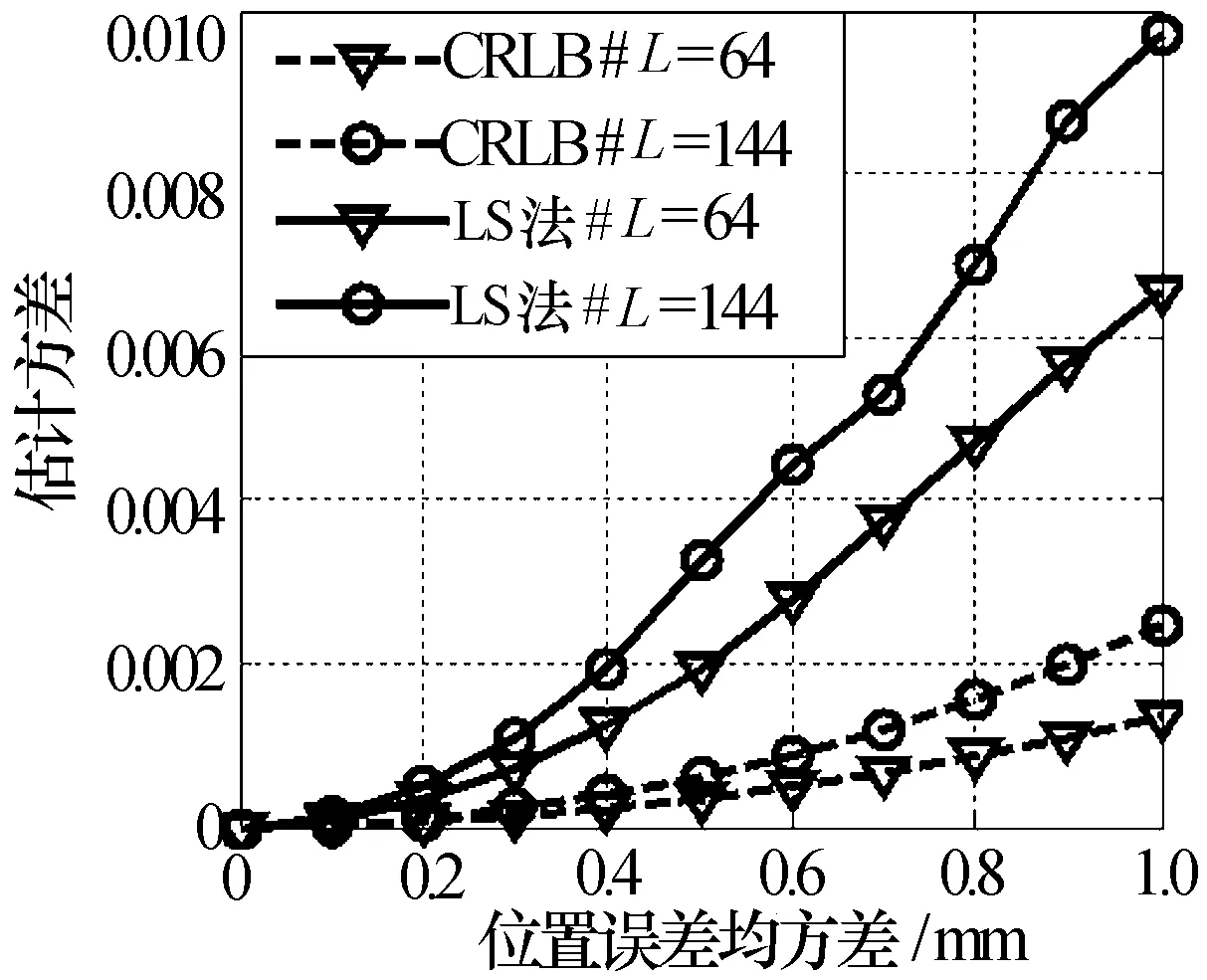
图12 不同成像单元数的方差曲线

5 结束语

阵元位置误差是阵列雷达中一个普遍存在的问题，本文针对雷达关联成像这一全新成像体制，研究了阵元位置误差的影响，得到了存在阵元位置误差下的雷达关联成像模型，导出了目标散射系数估计的CRLB，着重分析了阵元数、带宽等对成像误差的影响，使得雷达关联成像中各种因素之间的关系逐步清晰，对阵元位置误差的补偿具有一定的指导意义。

[1] MARGARET C, BRETT B. Fundamentals of radar imaging[M]. PA: SIAM, 2009.

[2] LI D, LI X, CHENG Y, et al. Radar coincidence imaging: an instantaneous imaging technique with stochastic signals[J]. IEEE Transactions on Geosciences and Remote Sensing, 2014, 52(4): 2261-2277.

[3] 何学智. 微波凝视关联成像的信息处理方法与仿真[D]. 合肥: 中国科学技术大学, 2013. HE Xuezhi. The information processing methods and simulations in microwave staring correlated imaging[D]. Hefei: University of Science and Technology of China, 2013.

[4] 李东泽. 雷达关联成像技术研究[D]. 长沙: 国防科学技术大学, 2014. LI Dongze. Research of radar coincidence imaging[D]. Changsha: National University of Defense Technology, 2014.

[5] 司伟建, 吴秀月. 阵列天线阵元位置误差的校正算法[J]. 应用科技, 2009, 36(1): 64-68. SI Weijian, WU Xiuyue. Calibration algorithm for sensor position error of array antenna[J]. Applied Science and Technology, 2009, 36(1): 64-68.

[6] 于 斌，尹成友，黄 冶. 基于模拟退火算法校正天线阵列位置误差[J]. 现代雷达，2007，29(10): 31-34. YU Bin, YIN Chengyou, HUANG Ye. Calibration for array position uncertainties based on simulated annealing[J]. Modern Radar, 2007, 29(10): 31-34.

[7] 于 斌，尹成友，沈 辉. 阵列误差对测向性能的影响及校正方法[J]. 现代雷达, 2007, 29(4): 34-42. YU Bin, YIN Chengyou, SHEN Hui. Effect and calibration of array errors among sensors in direction-finding[J]. Modern Radar, 2007, 29(4): 34-42.

[8] KAY S M. 统计信号处理基础--估计与检测理论[M]. 罗鹏飞, 译. 北京: 电子工业出版社, 2011. KAY S M. Fundamentals of statistical signal processing: Estimation and detection theory[M]. LUO Pengfei, trans. Beijing: Publishing House of Electronics Industry, 2011.

徐先武 男，1991年生，硕士研究生。研究方向为雷达成像、雷达信号处理等。

Analysis of Array Position Error in Radar Coincidence Imaging

XU Xianwu，CHENG Yongqiang，QIN Yuliang，ZHOU Xiaoli

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

As a novel high-resolution staring imaging technique, radar coincidence imaging (RCI) shows the great potentials in military applications. In this paper, the array position error which exists in array radar generally is considered; the RCI model in the presence of array position error is established. To obtain the analytic result, the nonlinear relationship between the echo and array position error is approximated linearly by the first-order Taylor expansion, thus the theoretical error bound of RCI with array position error is derived. Then the influences of several factors on imaging error are precisely predicted, including the number of array elements, signal bandwidth, the size and number of imaging cells, the coefficients and number of scattering centers. The conclusions and results could provide references for the parameter setup of RCI system and compensation of array position error.

array radar; radar coincidence imaging; array position error; CRLB

10.16592/ j.cnki.1004-7859.2016.03.007

国家自然科学基金资助项目(61302149, 6117133)

徐先武 Email：xianwu_xu@sina.com

2015-10-18

2015-12-20

TN957

A

1004-7859(2016)03-0032-06