基于压缩感知的多普勒超分辨模型研究

赵凯恒，伍光新，王建明

(南京电子技术研究所, 南京 210039)



·信号处理·

基于压缩感知的多普勒超分辨模型研究

赵凯恒，伍光新，王建明

(南京电子技术研究所, 南京 210039)

低脉冲重复频率(PRF)雷达是解决多目标多普勒模糊的关键技术之一，基于此雷达工作体制，提出一种基于压缩感知(CS)理论的多普勒超分辨处理方法，利用该方式下回波信号在相参积累时间内的时域欠采样特性及多普勒域的稀疏特性，构建了多普勒超分辨的CS模型，并采用正交匹配追踪算法对多目标进行超分辨处理。同时，提出了一种改进算法，即基于SVD分解的二次测量及动态感知联合优化算法模型，仿真结果验证了算法的有效性及可靠性。

多普勒超分辨；压缩感知；多重复频率；SVD分解；感知矩阵；动态感知

0 引 言

多普勒超分辨是信号处理中的重要研究内容之一，在雷达成像、机群分辨等军事领域尤为重要。传统的多普勒处理方式是将接收信号通过一个多普勒滤波器组来实现，相干积累时间的大小限制了多普勒分辨率的提高。若目标在雷达波束照射期间或者雷达波束处于扫描状态时发生越距离单元走动，目标的有效相干积累时间将受到极大的限制[1]。

2004年，Donoho与Cands等人提出压缩感知理论，一个充分利用信号稀疏性或可压缩性的全新信号采集与编解码理论。该理论表明，当信号具有稀疏性或可压缩性时，通过采集少量的信号投影值就可实现信号的准确或近似重构[2]。

在雷达场景中，由于目标在多普勒域的稀疏特性，因此可以应用压缩感知理论，在有限的相干积累时间内实现目标的多普勒超分辨[3]。然而稀疏字典的非正交性影响了多普勒信号的重构精度和重构概率，限制了其超分辨的能力。

基于此，本文提出一种动态感知联合优化算法模型(SVD-TSM DP)优化算法，其是在原超分辨模型的基础上增加一测量步骤，通过降低感知矩阵的相关性来提高重构概率和重构能力；同时，为了以最大概率重构出原始信号，提出一种动态生成测量矩阵的联合优化算法，相关理论框图如图1所示。

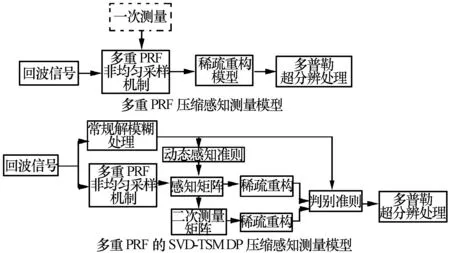
图1 多重PRF压缩感知模型与SVD-TSM DP优化模型对比图

1 多重PRF基本采样模型

脉冲重复频率(PRF)[4]是脉冲体制雷达的主要参数之一，本文在张玉玺等[5]提出的基于压缩感知理论的多普勒解模糊处理的基础上进行多普勒超分辨工作，模型的论证过程可参考文献[5]。

基于压缩感知的多普勒解模糊模型[5]为

min‖s‖1st.As=y

(1)

式中：s为信号多普勒频谱响应；y为慢时间域非均匀采样序列；A由雷达各PRF值、感兴趣目标的多普勒频率范围fmax、每个采样脉冲所对应的慢时间取样时刻tm(m= 0,1,…,M-1)、相参时间内总的脉冲采样数M以及多普勒频率抽样位置fn(n=0, 1,…,N-1)决定

(2)

当考虑噪声的情况，上述模型转化为

min‖s‖1st.As+n=y

(3)

式(3)即为本文进行多普勒超分辨的基础模型。

2 SVD-TSM DP算法

2.1 SVD矩阵优化

在压缩感知理论中，矩阵的RIP性质决定了信号的恢复能力，并且通过定义RIP常数来刻画某一矩阵性质的好坏[6]。

文献[6]中给出了判断一个矩阵是否满足RIP性质的计算也是比较繁琐和困难的。除RIP理论可以衡量一个矩阵处理稀疏信号的能力外，人们提出了相关性判别理论、矩阵Spark判别理论、测量算子零空间理论及k-neighborly理论等。在这些理论中，只有相关性判别理论能够较为直观地判别某一矩阵的形态[6]。因此本文主要通过相关性判别理论作为优化算法的前提。

感知矩阵A的各列间的互相关系数[7]可以用下式求得

S=AHA

(4)

式中：S对角线上为各列的自相关系数，其他元素为对应列之间的互相关系数，我们的目标是使S尽可能的逼近单位矩阵I，下面开始进行SVD优化算法理论分析。

基于压缩感知理论的多重复频率信号多普勒信号超分辨的求解模型为

min‖s‖1st.As+n=y

式中：A为M×N矩阵；s为N×1向量，M远远小于N。为了保证模型的重构能力，我们在选取雷达PRF参数时保证A行满秩条件。

现在对以上模型两边同时乘以一个M×M的矩阵Ψ，此处称之为优化矩阵，得到新的方程为y′=ΨAs，另y′=y，得y=ΨAs，我们的最终目标是使新得到的压缩感知矩阵ΨA的相关矩阵近似逼近单位阵。

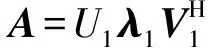
S=BHB=AHΨHΨA

(5)

整理得

(6)

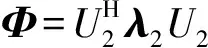
(7)

(8)

将λ1=[λΘ] 代入式(8)得

(9)

由于λ和λ2均为对角阵，另

(10)

(11)

式(9)可以写为

(12)

由于V1为酉矩阵，因此令

βi=1/|αi|2， i=1,2,…,M

(13)

则S近似为单位阵。因此我们得到

(14)

因为Φ=ΨHΨ，所以我们另

(15)

我们得到了二次测量矩阵Ψ基于原始测量矩阵A的表达式。

基于压缩感知理论的多重复频率信号多普勒信号超分辨的二次测量求解模型模型为

min‖s‖1st.ΨAs+Ψn=y

(16)

称之为SVD-STM算法模型。

2.2 SVD-TSM DP算法

在SVD-STM模型中，由于稀疏字典的冗余性，使得SVD-TSM算法的性能大大降低，同时OMP算法[8]具有很复杂的运算，使得本算法执行效率偏低。因此，提出一种动态矩阵形成的联合优化算法。本算法首先通过常规多普勒解模糊方法确定目标多普勒位置，然后根据目标的多普勒位置动态选择多普勒频率值f，再由f确定压缩感知算法所需的感知矩阵，此时模型的稀疏字典由于只包含目标位置附近的稀疏基向量，因此对于分辨率相同的情况下，由于多普勒频率范围的缩小，N可以选择相对较小的值。在此基础上进行原始压缩感知模型的多普勒超分辨处理以及二次测量多普勒超分辨处理，根据常规解模糊处理的结果选择重构效果最好的一个，从而得到我们想要的超分辨处理结果。算法流程图如图2所示。

动态生成感知矩阵的规则为：首先，确定稀疏字典的规模，即选定M和N；然后，应用常规多普勒解模糊算法得出多普勒频率所在的num个位置；第三步，根据所得的频率大概位置在每个频率点附近开频率窗，频率窗大小为L=N/num，如图3所示。

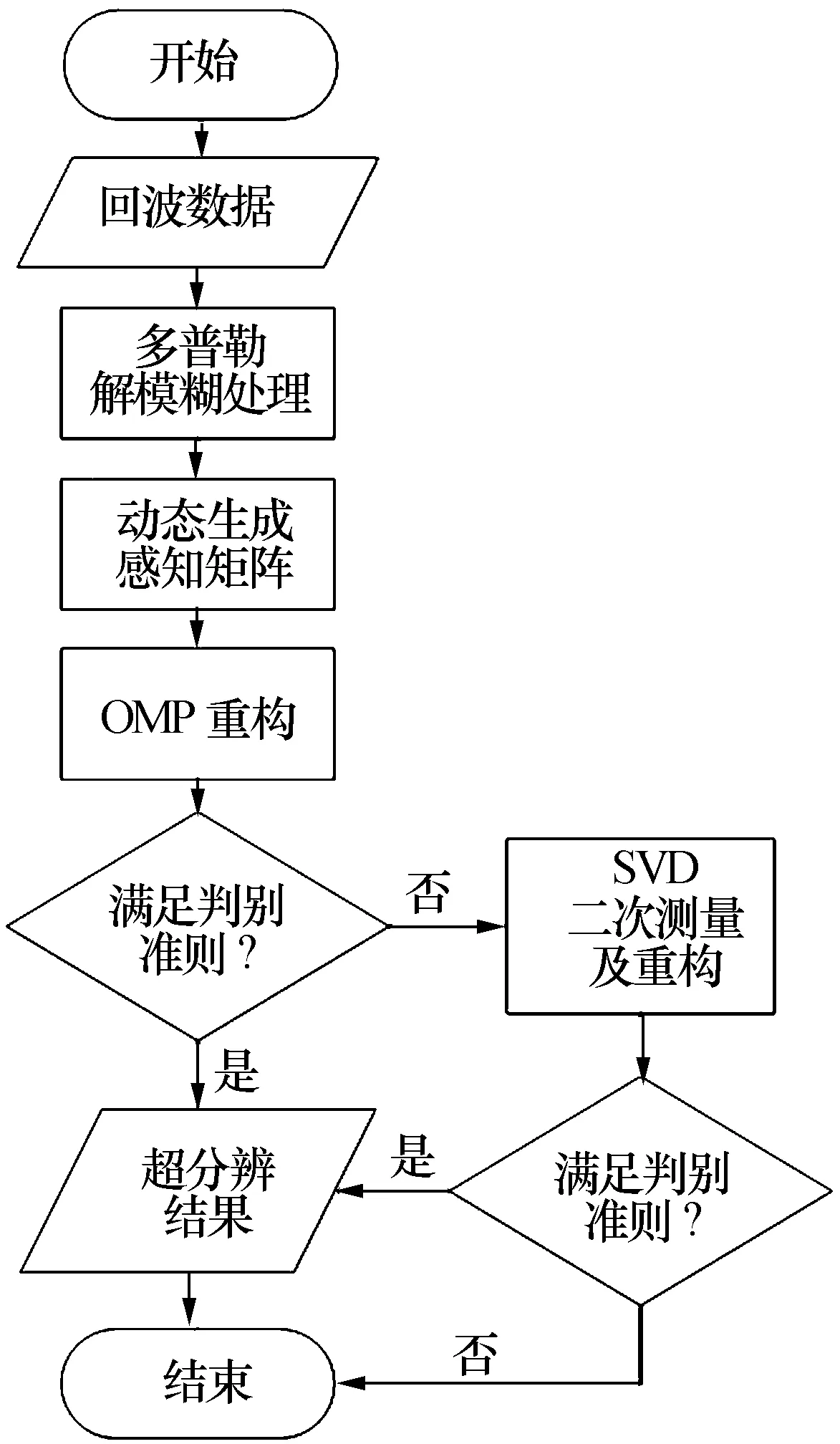
图2 SVD-TSM DP算法流程图

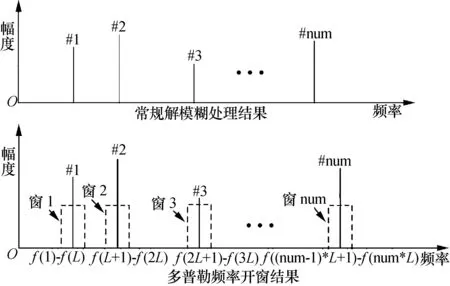
图3 多普勒频率开窗示意图

判别规则为：将相同窗内的多普勒超分辨处理结果与常规解模糊处理结果的频率进行比较，小于偏离门限则超分辨结果成功。

3 仿真分析

对于多重参差方式，仿真所采用的三种PRF值分别为fr1=1 048 Hz，fr2=905 Hz，fr3=1 097 Hz；每种PRF发射的子脉冲数为85个，总相参处理时间内的脉冲数为M=255。通过分析可知常规算法的分辨率为10 Hz左右。

3.1 矩阵RIP性质验证

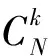
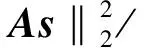
(17)

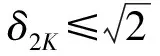
采用本文上述基于压缩感知理论的多普勒超分辨处理， 设置多普勒门宽度Δf =0.8Hz、2.4Hz、5.6Hz、10Hz，N=2 000，频率范围从0-Δf ×N。按式(2)构造CS矩阵A，对不同K-稀疏情况下的RIP属性验证结果如图4所示，随机验证次数为10×K ×N次[4]，RIC近似值按式(17)计算。根据图4的结果，超分辨处理中所用的确定型CS矩阵A在Δf=0.8Hz时不满足无失真条件，在其他Δf处满足无失真重构条件，并且SVD优化算法可以提高矩阵的RIP性，相较未优化前有更好的重构性能，可以保证对多普勒谱s的有效估计。

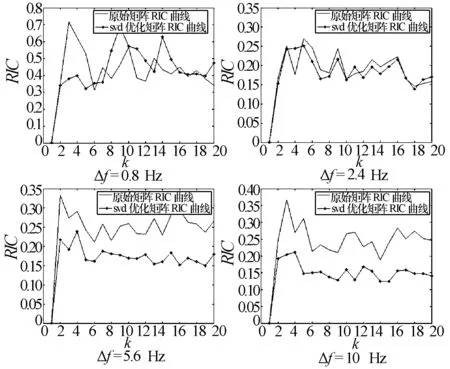
图4 RIC近似值

3.2 SVD-TSM DP算法仿真验证

3.2.1 相邻目标分辨能力仿真实验

设定k=2，M=255，原始超分辨模型、SVD-STM模型采用N=2 000，SVD-STM DP模型多普勒频率总的窗大小选择N= 500，多普勒分辨率Δf从0.4到10，不加噪声，通过蒙特卡洛实验来统计其在不同多普勒分辨率下原始超分辨模型、SVD-STM模型和SVD-STM DP模型的重构概率，重建算法采用OMP算法，结果如图5所示。

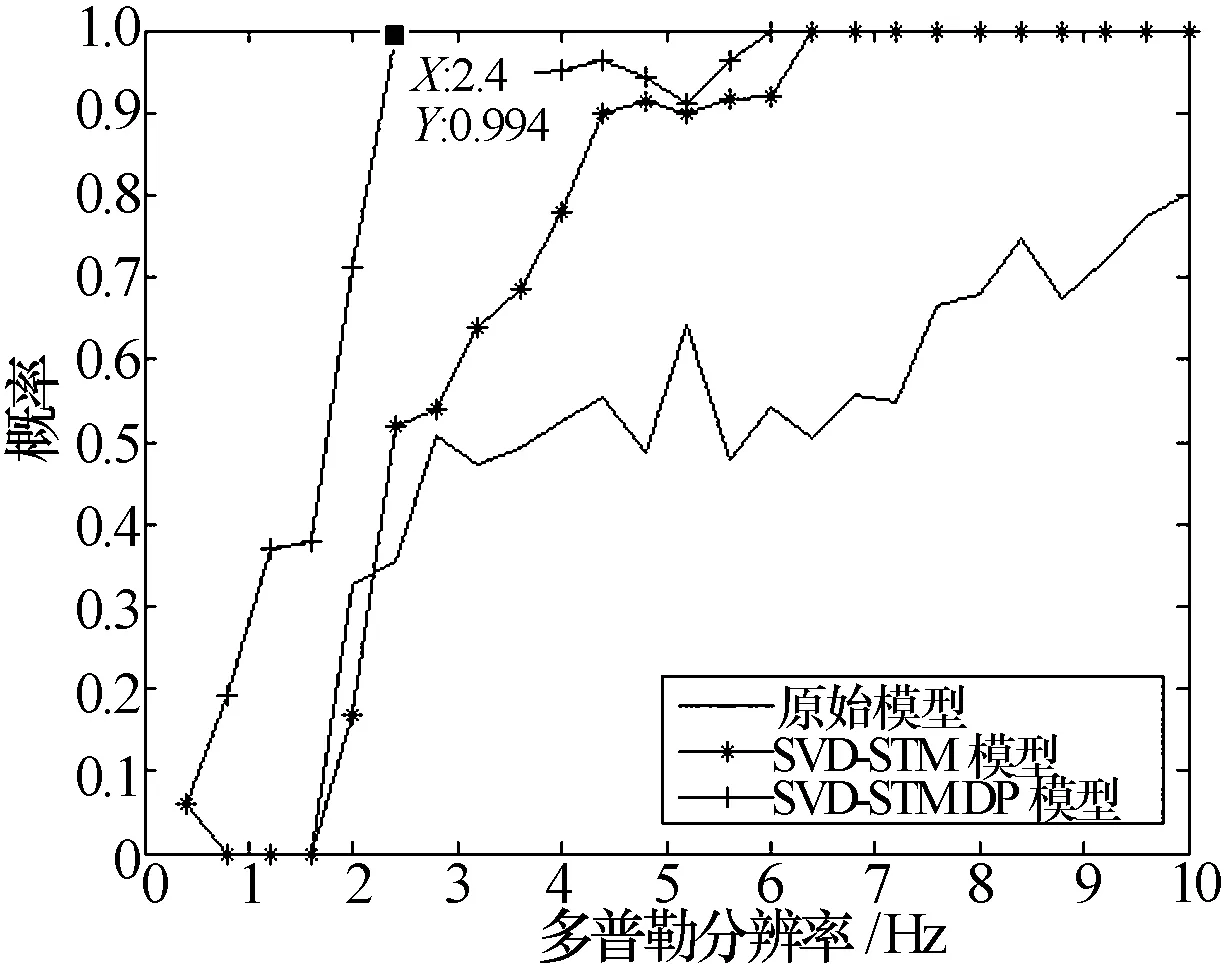
图5 不同多普勒分辨率情况下三种模型重构概率对比图

如图所示，多普勒分辨率大于2 Hz时，SVD-STM算法效果明显优于原始模型，并且当多普勒分辨率大于6 Hz时重构概率100%，而在小于2 Hz时原始模型优于SVD-STM算法，而SVD-STM DP算法则综合利用了两种模型的优点，重构性能大幅提升，尤其在分辨率为2.4 Hz时重构概率达到了99.4%，明显优于传统处理算法的分辨率。

3.2.2 多个目标分辨能力仿真实验

设定M=255，原始超分辨模型、SVD-STM模型采用N=2 000，SVD-STM DP模型多普勒频率总的窗大小选择N=500，分辨率为2.4 Hz，k从1到20，不加噪声，通过蒙特卡洛实验来统计其在不同稀疏度下原始超分辨模型、SVD-STM模型和SVD-STM DP模型的重构概率，重构算法采用OMP算法，结果如图6所示。

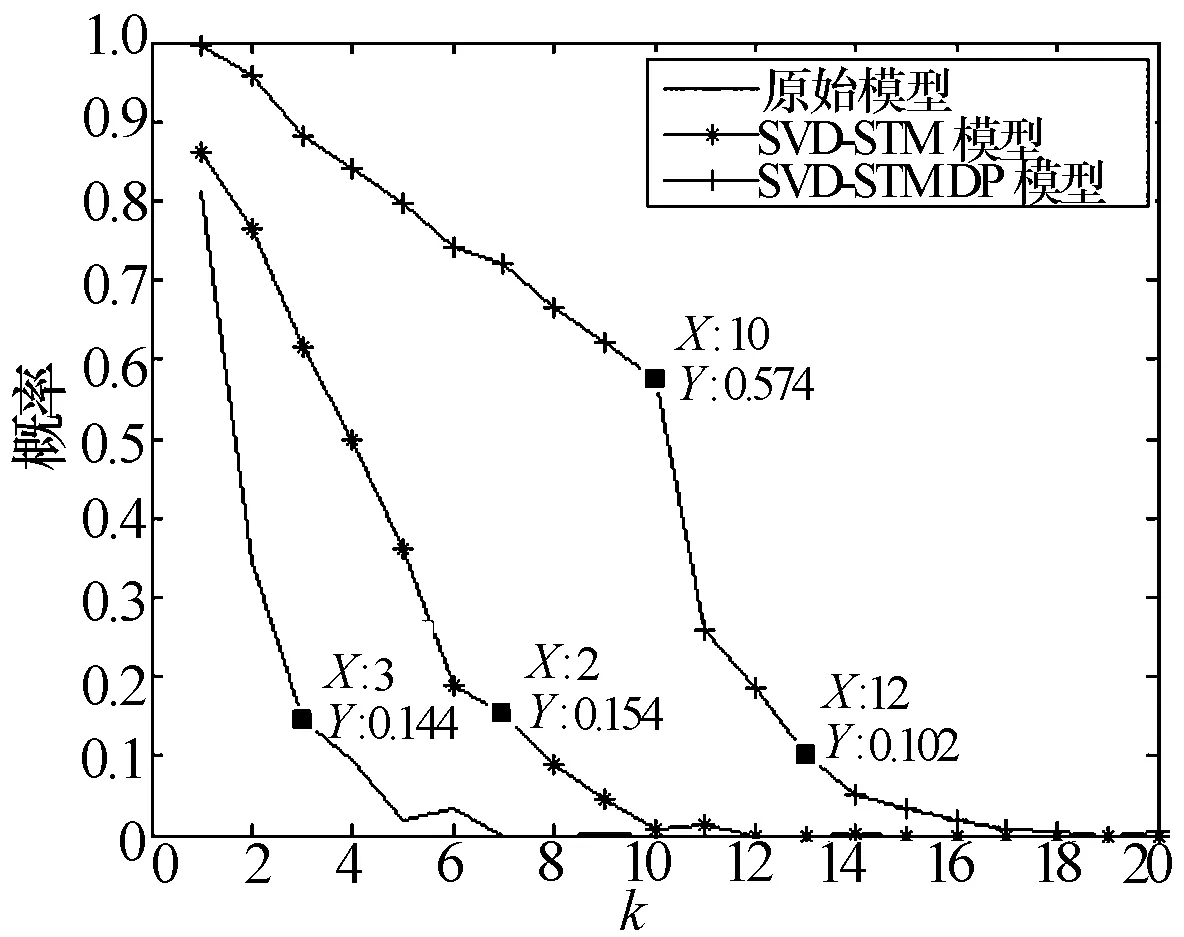
图6 不同稀疏度情况下三种模型重构概率对比图

如图6所示，原始模型在稀疏度为3时其重构概率已经降到了14.4%，而SVD-STM模型的重构性能相比原始模型有了很大提高。当k=7时，重构概率降到了15.4%，而基于动态感知的SVD-STM DP算法相对前两种算法其性能有了显著提升；当k=10时，其重构概率为57.4%；当k=13时，其重构概率降到了10.2%，其多目标分辨能力有了显著提升。

3.2.3 不同信噪比下重构性能仿真实验

设定M=255， SVD-STM DP模型多普勒频率总的窗大小选择N=500，分辨率为2.4 Hz，k=2，目标多普勒频率为f1=69.6 Hz,f2=530.4 Hz，信噪比从0 dB到40 dB，对SVD-STM DP进行仿真，统计的相对误差如图7所示。

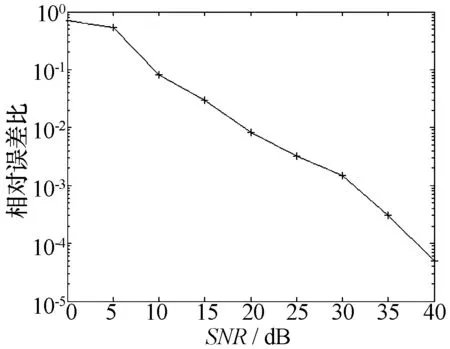
图7 不同信噪比下SVD-STM DP算法相对误差性能曲线

由图7所示，当信噪比大于0 dB的时候，相对误差随着信噪比的增加线性减小，当信噪比大于10 dB时，相对误差比降到10%以内，20 dB时相对误差比降到1%以内，因此本算法在信噪比大于0 dB时具有较好的性能。

4 结束语

本文提出了基于压缩感知的多普勒超分辨模型，感知矩阵满足RIP条件。提出的SVD-STM DP算法本质上采用SVD分解进行感知矩阵的RIP性能优化，改善了传统压缩感知重构算法的适用范围，提升了同时多目标分辨能力，能够在低信噪比环境下适用，且明显降低了运算量，相对传统多普勒处理算法具有更高的分辨率及更优的估计性能，是一种适应性很强的超分辨算法。

[1] 刘记红, 徐少坤, 高勋章,等. 压缩感知雷达成像技术综述[J].信号处理，2011，27(2): 252-260. LIU Jihong, XU Shaokun, GAO Xunzhang, et al. A review of radar imaging technique based on compressed sensing[J]. Signal Processing，2011，27(2): 252-260.

[2] 汪 祺. 压缩感知综述[DB/OL]. [2015-03-01]. http://wenku.baidu.com/view/3c058397dd88d0d233d46af7.html，2011. 10.20. WANG Qi. A review of compressed sensing[DB/OL].[2015-03-01].http://wenku.baidu.com/view/3c058397dd88d0d233d46af7.html，2011.10.20.

[3] CANDES E. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory，2006，52(2): 489-509.

[4] 屠亚兰. 非均匀采样信号重构技术及其在PD雷达HPRF信号处理中的应用[J]. 现代雷达，1997, 19(2): 84-87. TU Yalan. Reconstruction techniques of signals nonuniformly sampled and its application to PD radar signal processing in HPRF[J]. Modern Radar，1997, 19(2): 84-87.

[5] 张玉玺, 孙进平, 张冰尘, 等. 基于压缩感知理论的多普勒解模糊处理[J]. 电子与信息学报，2011，33(9): 2103-2107. ZHANG Yuxi, SUN Jinping, ZHANG Binchen, et al. Doppler ambiguity resolution based on compressive sensing theory[J]. Journal of Electronics & Information Technology，2011，33(9): 2103-2107.

[6] 徐志强. 压缩感知[DB/OL].[2015-03-01]. http://3y.uu456.com/bp-47dfe211866fb84ae45c8db5-1.html,2012.1.12. XU Zhiqiang. Compressive sensing[DB/OL].[2015-03-01]. http://3y.uu456.com/bp-47dfe211866fb84ae45c8db5-1.html，2012.1.12.

[7] 贺亚鹏, 朱晓华, 庄珊娜, 等. 压缩感知雷达波形优化设计[J]. 南京理工大学学报，2011，35(4): 519-524. HE Yapeng, ZHU Xiaohua, ZHUANG Shanna, et al. Optimal waveform design for compressive sensing radar[J]. Journal of Nanjing University of Science and Technology，2011，35(4): 519-524.

[8] TROPP J A, GILLBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory,2007,53(12):4655- 4666.

赵凯恒 男，1988年生,硕士研究生。研究方向为压缩感知,雷达总体系统研究等。

伍光新 男, 1980年生,博士,高级工程师。研究方向为相控阵雷达总体技术, 雷达目标识别技术等。

王建明 男，1970年生，博士,研究员级高工。研究方向为雷达系统工程，自适应阵列处理等。

A Study on Doppler Super Resolution Algorithm Model Based on Compressive Sensing

ZHAO Kaiheng，WU Guangxin，WANG Jianming

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

Low pulse repetition frequency (PRF) radar is one of the key technologies for Doppler ambiguity resolution of multiple targets. With the traditional radar system, a Doppler super resolution method based on compressive sensing is proposed. Under the analysis of the sub sampling characteristics in time domain and sparse characteristics in Doppler domain during the coherent processing interval, the CS model of Doppler super resolution is established,and the OMP algorithm is used in the processing. On the basis of the original algorithm, an improved algorithm is proposed named joint optimization algorithm of SVD-two step measurement and dynamic perception (SVD-TSM DP), and the simulation results verify the effectiveness and reliability of the improved algorithm.

Doppler super resolution; compressive sensing; low pulse repetition frequency; singular value decomposition; sensing matrix; dynamic perception

10.16592/ j.cnki.1004-7859.2016.03.008

赵凯恒 Email：zkheng2010@126.com

2015-10-11

2015-12-18

TN911.7

A

1004-7859(2016)03-0038-05