基于化归思想的高中数学教学策略微探

曹远慧 ●

江苏省仪征中学(211400)



基于化归思想的高中数学教学策略微探

曹远慧 ●

江苏省仪征中学(211400)

化归思想是重要的数学思想方法，在教学过程中化归思想不应该被我们教师灌输和硬塞给学生，而应该通过情境的设置和引导学生结合自己的原有知识结构和图示进行整合与迁移，在学习知识和解决问题的过程中逐步地领悟化归思想的本质.

化归思想；高中数学；能力

一、夯实基础是前提

“巧妇难为无米之炊”，学生要想学好高中数学，首先必须夯实基础，如何帮助学生夯实基础呢？我们在教学过程中可以从如下几个方面着手.

1.研读教材

教材是最好的例子！承载着基础知识和基本方法，而如果放手让学生自己去阅读教材，缺乏必要的指导的话，学生的信息阅读和提取往往浮于文字表面.因此为了促进学生基础的夯实，我们教师必须在学生阅读教材之前对教材文本进行细致地研读，研读后尝试着用问题的形式，引导学生把教材中零星的知识聚到一块，串接起来；或是设置特定的情境引导学生在情境中分析，提高学生运用知识分析和解决问题的能力，感受化归的思想方法.

2.启发式教学

学生具有的化归意识和能力是无法灌输的，必须给学生创设有利于学习化归思想方法的条件，坚持启发式教学，让学生的意识、能力的发展水到渠成.

注重启发式教学，学生的注意力会由记教师的内容转到思考数学问题，会自觉地对照自己的原有认知和解决问题的经验，学生的迁移能力长期处于较高的水平.

二、培养品质是动力

好的思维品质才能很好地感受化归思想方法的精髓.在教学过程中，我们培养学生的思维品质应从如下几个方面着手.

1.过程性变式，提高学生解决数学问题的程序性

从“化归思想方法”所具有的特点来看，“多向性”和“重复性”显得尤为突出，纵观我们当前的数学考题，通常情况下化归对象显得陌生、复杂而且凌乱，学生很难一眼看到熟悉的、简单的模型，导致问题的转化往往出现困难，笔者认为化归的过程本身就难以一蹴而就，为了促进学生化归思维品质的提升，我们在问题的设置上，可以进行适当的铺垫，尤其是在过程上进行逐层变式处理和引导，使学生拾级而上从已知问题逐步化归推向未知问题，解决问题的过程中形成清晰的认识，同时提升解决数学问题的能力.

例如，我们可以设置如下的变式练习，让学生在解决问题的过程中类比、联想，促进知识、方法的迁移.

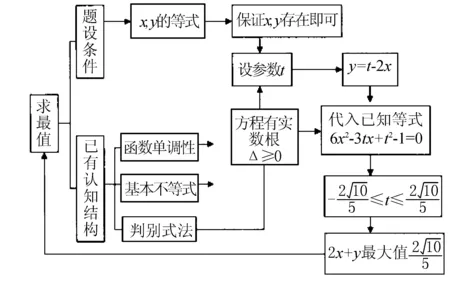
例2 设1

设计意图 这两个例题属于并列变式的结构，例1属于“分式不等式”，例2属于“对数不等式”，看似没有联系，但是放在一块，学生能够看到有相似之处：两个例题的布局以及不等号的方向都完全一致，而对于学生解题的难易程度来看，解决例1相对容易一些，再由此类比，将解例1的方法和经验用于解决例2，给例2提供了化归的模型、目标和方法.

2.注重知识形成过程的渗透

知识的形成不是一蹴而就地，我们应该引导学生体验概念产生和发展的过程，借此提升学生的思维品质.

例如，从结构上看，“棱柱、棱锥、棱台”与“圆柱、圆锥、圆台”相比存在着较大的差异，差异在哪里？在底面，如果底面发生变化时，可以发现他们能够互相转化，让学生自主体验这种转化过程，并以思维导图的形式呈现.

三、解决问题是途径

数学学习离不开解决数学习题和数学问题，解题是一条有效提高学生化归能力的途径，如何培养呢？笔者认为，不能仅仅要求学生得到答案，而应该将化归的思想方法渗透到分析问题特征，提取原有认知，发现解题思路和解决问题的整个过程.

例3 设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值为____.

分析 例3这个问题的解决方案较多，可以借助于基本不等式解决问题，也可以借助于“判别式法”求解，我们在这道问题的讲评过程中如果仅仅满足于答案，显然对于学生化归思想方法的培养是不够的，笔者认为可以借助于这个例题，将探究解题思路的整个思维过程可视化呈现(如图所示).

实践经验表明，如果我们在教学过程中，尤其是解决问题环节，重点抓住学生的思维过程，那么学生在学习过程中就会将重心放在思维品质和程序性知识的一般解决方法上，这将是良性的学习方式.

G632

B

1008-0333(2016)24-0025-01