平面柔性铰链机构自动建模方法

李佳杰，刘小院，陈贵敏

(西安电子科技大学 机电工程学院，陕西 西安 710071)



平面柔性铰链机构自动建模方法

李佳杰，刘小院，陈贵敏

(西安电子科技大学 机电工程学院，陕西 西安 710071)

从图论的基本概念出发，得到了柔性铰链机构有向图表示，并针对平面柔性铰链机构提出一种改进的双色图表示方法．通过十字链表的数据结构形式将柔性铰链机构的双色图表示映射到计算机中，按照所需的运算顺序遍历双色图，依次调用相应的函数表达式，从而实现了柔性铰链机构运动静力学模型的自动生成．以差分微位移放大机构为例，将基于图表示的平面柔性铰链机构自动建模方法计算结果与有限元仿真分析结果对比，两者的相对误差为4.89%，表明该自动建模方法是可行的．

平面柔性铰链机构;图论;自动生成

柔性铰链机构是用柔性铰链替代传统的运动副来连接刚性构件并利用其弹性变形实现运动的集中柔度式柔顺机构[1]．柔性铰链机构具有无机械摩擦、无间隙、无需润滑及分辨率高等优点，在现代传动系统、光学系统、医疗设备、生物工程、集成电路制造和微细加工等宏观及微观领域中被广泛应用[2]．

柔性铰链机构的建模是分析柔性铰链机构性能的基础．文献[3]基于伪刚体模型对集中柔度式柔顺机构进行了建模、分析与综合．文献[4]提出了一种扩展的伪刚体模型法，求解全柔性机构的位置解．文献[5]结合虚功原理和伪刚体模型建立了柔性铰链机构的静力学模型，并基于所提出模型设计了一种新型位移放大/缩小柔性铰链机构．文献[6]考虑压电叠堆产生的输入力对柔性机构输出位移的影响，建立了柔性铰链机构的静力学模型．文献[7]提出了一种确定柔性铰链机构位置的迭代方法，并进行了柔性铰链机构的运动学分析和静力学分析．伪刚体模型由于忽略柔性铰链的线位移变形，精度不高，而文献[7]提出的迭代算法主要用于分析简单的连杆机构．因此笔者以平面柔性铰链机构为研究对象，在图表示法的基础之上，提出一种平面柔性铰链机构改进的双色图表示，更为清晰和准确地反映柔性铰链机构的拓扑关系．按照所需的运算顺序遍历双色图的顶点和边，即可依次调用相应的函数表达式，最终实现了柔性铰链机构运动静力学模型的自动生成．

1 柔性铰链机构图表示法

柔性铰链机构由刚性杆通过柔性铰链连接组成，而图是由点通过边连接组成[8]．因此，刚性杆与点、柔性铰链与边之间形成对应关系．给定一个机构，必然可得到一个描述它的图．将柔性铰链机构的刚性杆用顶点表示，铰链用有向边(弧)表示，则得到柔性铰链机构的有向图．为便于描述，作以下约定: 输入杆对应的顶点为根顶点并作为图的第1层，输入杆邻接的刚性杆对应的顶点放置在第2层，当同一层有多个顶点时则依据实际连接位置排列; 与第2层顶点邻接的顶点放置在第3层，依此规律确定所有顶点在图中的相对位置．相邻接的顶点之间用有向边连接，箭头由上层指向下层．因此，所得到的图表示具有以下特性:

(1) 方向性: 柔性铰链机构的有向图表示从输入端指向输出端;

(2) 连通性: 柔性铰链机构常常是一体化加工而成，因此其对应的图中不存在孤立顶点，且存在一条或多条从根顶点到叶顶点的通路;

(3) 严格的层次关系: 柔性铰链机构中各构件层次关系明显，即在图表示中不同构件所对应的点和边应依据某些规律分层排列．

根据上述约定，图1为差分微位移放大机构及其有向图表示．

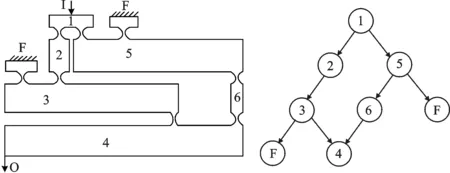
图1 差分微位移放大机构及其有向图表示

2 柔性铰链机构尺寸特征定义

通常一个柔性铰链只连接两个刚性杆，因此，柔性铰链可由4位组成的惟一标识符[9]表示: 第1位是字母“h”，表示柔性铰链; 第2位是与铰链连接的前一个杆号; 第3位是连接符“-”; 最后一位是与铰链连接的后一个杆号．例如，连接杆2和杆3的铰链命名为h2-3．柔性铰链的长度用L表示，方向角由α表示(角度和角位移均以逆时针为正)．

柔性铰链机构中常见的刚性杆有二副杆、三副杆和多副杆．对于二副杆，杆长就是两个铰链之间的距离．一般情况下，三副杆会有两条路径通过，根据在刚性杆上且同路径方向的两个铰链确定一个距离，由两端柔性铰链给其命名，也是惟一的．刚性杆标识符有6位: 第1位是字母“R”，表示刚性杆; 第2位～第4位是前一个铰链的名字并省略首字母h; 第5位是连接符“-”; 第6位是后一个铰链名字的末位．例如，在杆3上由铰链h2-3到铰链h3-4的这段路径命名为R2-3-4．输入杆由输入端和其连接的铰链编号命名．输入端用字母“I”表示，输入杆的标识符记为RI-1-×; 类似地，机架用字母“F”表示，输出端用字母“O”表示．刚性杆长度用d表示，其在全局坐标系下的方向角用θ表示．

根据上述命名规则，图2给出了差分微位移放大机构所有尺寸特征的定义．

图2 差分微位移放大机构各构件命名及其角度定义

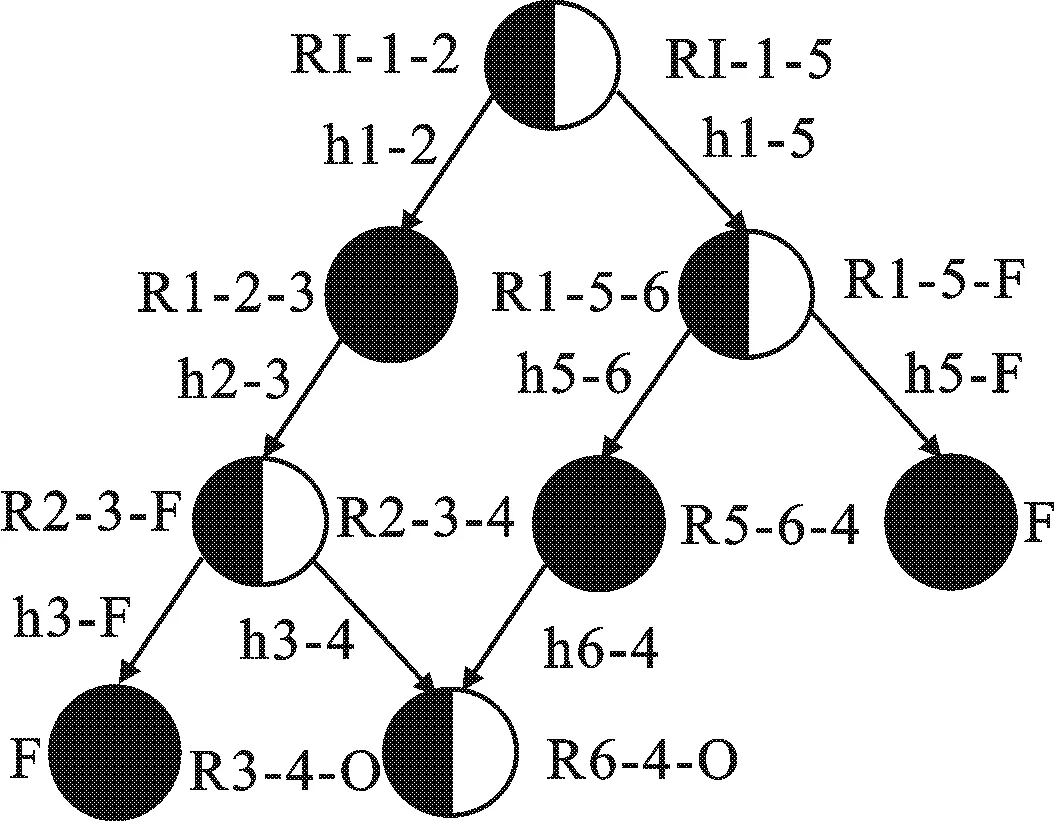
图3 差分微位移放大机构改进双色图表示

3 柔性铰链机构的改进双色图表示

常规的双色图[10]以黑色顶点表示刚性杆，以白色顶点表示柔性铰链，当一柔性铰链与某刚性杆连接时，则用一条边将它们各自对应的白色顶点和黑色顶点相连接．但是单色图表示和常规双色图表示只是简单地将杆与铰链的连接关系表示出来，并没有把柔性铰链机构的尺寸特征(参与计算的刚性杆长度)通过图表示加以区别．为此，笔者提出一种改进的双色图表示，其建立规则为: 以黑色实心顶点‘●’表示常规杆(入度和出度都不大于1的点)，以左黑右白顶点‘’表示分歧杆或汇聚杆，当机构中有多副杆时，可将双色顶点根据所需拓展到三色或多色; 以弧表示柔性铰链，当两刚性杆之间有柔性铰链直接连接时，两构件对应的两顶点之间用一条弧连接．图3为差分微位移放大机构的改进双色图表示．

4 柔性铰链机构的运动静力学模型

分析与求解柔性铰链机构，需从3个方面考虑:静力学，几何学和柔性铰链的载荷-变形[11]．即综合了静力平衡方程、变形协调方程(几何方程)和柔性铰链的载荷-变形方程．

图4 单个铰链的受力分析

4.1 静力平衡方程

柔性铰链机构中除柔性铰链外，其余部分都视为刚体．对单个柔性铰链可视为一端固定、另一端自由的梁单元进行受力分析，如图4所示(O点为固定端、A点为自由端)．

设柔性铰链在A点处受载荷F=[Fx，Fy，M]T作用，B点为变形后铰链末端位置，铰链的相应变形 X= [Δx，Δy，Δα]T，则在图4所示总体坐标系xOy下，柔性铰链末端B点位置坐标为

设刚性杆i末端与柔性铰链j连接，当刚性杆i转动一定角度后，其在总体坐标系下位置坐标为

其中，di为刚性杆i的长度，θi为初始角度，Δθi为角位移．柔性铰链j变形后在总体坐标系下位置坐标为

其中，Lj为柔性铰链j的长度，αj为初始角度，Δxj和Δyj为铰链末端沿x轴和y轴方向的线位移．

设差分微位移放大机构中各个柔性铰链所受载荷Fj=[Fxj，Fyj，Mj]T，给输入端Y方向施加的载荷为FI，按层分布写出其静力平衡方程．因篇幅有限只列出第1层平衡方程．

4.2 几何方程

柔性铰链机构受力后输出端位移应等于输入端位移与各构件变形的矢量和．当给柔性铰链机构施加载荷时，刚性杆i的位置坐标变化量为

而刚性杆i末端连接的柔性铰链j的位置坐标变化量为

因此，各条路径的几何方程为输入端位移、刚性杆位置变化和柔性铰链变形的累加，最终得到整个柔性铰链机构的几何方程．差分微位移放大机构的第一条路径几何方程如下:

4.3 柔性铰链的载荷变形方程

当柔性铰链局部坐标系与机构的总体坐标系不平行时，局部坐标系下柔性铰链的柔度矩阵需要通过旋转变换矩阵R转换到整体坐标系下，即

其中,

其中，K=C-1，是铰链的刚度矩阵．

图5 十字链表存储结构：顶点结构和弧结点结构

5 自动建模的软件实现

5.1 柔性铰链机构数据存储

为实现柔性铰链机构运动静力学模型的自动生成，首先要使柔性铰链机构的双色图表示准确无误地映射到计算机内存中．在数据结构中，十字链表是有向图的一种链式存储结构．在十字链表表示法中，顶点表的结点结构和边表的弧结点结构分别如图5所示．

顶点结点包含3个域: Vertex存储与顶点相关的信息，用于描述刚性杆特征: 顶点的名称、杆长、初始角度; Firstin指示该顶点的第1条射入弧; Firstout指示该顶点的第1条射出弧．

弧结点包含5个域: TailVertex和HeadVertex分别指示弧尾和弧头两个顶点在图中的对应位置; HeadNext指向与之具有相同弧头的下一条弧; TailNext指向与之具有相同弧尾的下一条弧; Info保存该弧的相关信息: 铰链名称和几何参数．

5.2 遍 历

就本质而言，遍历是一种模式，可以直接应用图已有的遍历算法或根据要求定义新的遍历算法．

广度优先搜索是一个分层的搜索过程，从图的第1层开始，从上至下逐层遍历，在同一层中，则按从左至右的顺序对顶点逐个访问．图的广度优先搜索最终输出一组顶点的连续序列，而机构的变形与柔性铰链有密切关系，需将刚性杆和其连接的铰链设为一组，对应于图中就是顶点和其连接的边，因此只需在广度优先搜索的基础上将弧的编号随关联顶点的编号一同并按层输出，将此过程称为“柔性铰链机构的层遍历”．

在有向图中，从顶点v0到顶点vn的一条路径是图的一个点弧交替序列(v0e1v1e2…vn-1envn)，其中vi-1和vi分别是弧ei的始点和终点，i=1，2，…，n．机构中输入杆对应图的根顶点，机架和输出杆都对应叶顶点．一般根顶点为一个，叶顶点有多个，由根顶点到叶顶点的所有路径记为基本路径组P，从根顶点出发，只能沿着弧的正方向行走，如果遇到分岔的多条弧要选择，则按从左至右的顺序优先选择最左边的岔道，并做标记，然后继续向下直至一个叶顶点．此时，第1条路径搜索结束．如果图中存在其他叶顶点没有遍历，则继续从根顶点开始，遇到分岔路时，从未标记过的岔道向下搜索，当搜索至叶顶点时结束; 如果图中还存在一条从根顶点到叶顶点的其他路径未遍历，则继续从根顶点开始，直至图中所有顶点和弧都查找过为止．

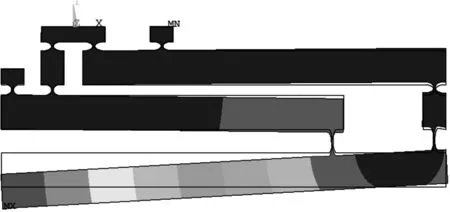
图6 差分微位移放大机构变形图

通过对图进行层和基本路径组的遍历在计算机中实现机构函数表达式．将刚性杆和柔性铰链相应的计算方程封装在各自对应的结点内，用图的遍历结果调用各个函数表达式．柔性铰链机构的静力平衡方程是按层遍历的顺序依次调用对应的u和v函数，几何方程是根据基本路径组调用Δu和Δv函数．只要按照机构的图表示正确遍历各个结点，并按顺序调用各个结点中对应的子函数完成各种分析的相关计算，从而实现柔性铰链机构的自动建模．

6 建模结果

差分微位移放大机构中柔性铰链为椭圆弧-倒角型柔性铰链[12]，材料选用45#钢，其杨氏模量为 200 GPa，泊松比为0.3，输入位移为 0.001 mm，其有限元分析得到的变形图如图6所示．基于图表示的平面柔性铰链机构自动建模方法计算结果和有限元方法计算结果见表1．

表1 自动建模法和有限元法结果对比

表1中的数据表明: 自动建模方法和有限元方法计算结果的相对误差为4.89%．理论解与仿真解之间存在一定的偏差，这是由模型的简化造成的．在建模过程中，忽略了柔性铰链机构中除柔性铰链外的其他部分的微小变形．

7 结 束 语

将图论这一数学理论应用到平面柔性铰链机构自动建立运动静力学模型中，拓展了图论在工程技术方面的应用范围．笔者从图论的基本概念出发，针对平面柔性铰链机构提出一种改进的双色图表示方法．通过十字链表的数据结构形式将柔性铰链机构的图表示映射到计算机中，按照所需的运算顺序遍历双色图，即可依次调用相应的函数表达式，最终实现了柔性铰链机构运动静力学模型的自动建立．以差分微位移放大机构为例，基于图表示的平面柔性铰链机构自动建模方法计算结果与有限元仿真分析结果对比，两者的相对误差为4.89%，表明该自动建模方法是可行的．

[1] HOWELL L L. Compliant Mechanisms[M]. New York: John Wiley & Sons, 2001.

[2]勾燕洁, 陈贵敏, 贾建援. 柔顺五杆三稳态机构的设计方法[J]. 西安电子科技大学学报, 2015, 42(4): 57-62.

GOU Yanjie, CHEN Guimin, JIA Jianyuan. Design Approach for a Compliant Five-bar Tristable Mechanism[J]. Journal of Xidian University, 2015, 42(4): 57-62.

[3]HOWELL L L, MIDHA A. Loop-Closure Theory for the Analysis and Synthesis of Compliant Mechanisms[J]. Journal of Mechanical Design, 1996, 118(1): 121-125.

[4]于靖军, 毕树生. 基于伪刚体模型法的全柔性机构位置分析[J]. 机械工程学报, 2002, 38(2): 75-78.

YU Jingjun, BI Shusheng. Kinematics Analysis of Compliant Mechanisms Using the Pseudo-rigid-body Model[J]. Journal of Mechanical Engineering, 2002, 38(2): 75-78.

[5]MENG Q L, LI Y M, XU J. A Novel Analytical Model for Flexure-based Proportion Compliant Mechanisms[J]. Precision Engineering, 2014, 38(3): 449-457.

[6]CHOI K B, LEE J J. Static Model for Flexure-based Compliant Mechanism Driven by Piezo Stacks[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2008, 222(4): 703-709.

[7]VENANZI S, GIESEN P. A Novel Technique for Position Analysis of Planar Compliant Mechanisms[J]. Mechanism & Machine Theory, 2005, 40(11): 1224-1239.

[8]王桂平, 王 衍, 任嘉辰. 图论算法理论、实现及应用[M]. 北京: 北京大学出版社, 2011.

[9]PARRISH B E, MICHAEL MCCARTHY J, EPPSTEIN D. Automated Generation of Linkage Loop Equations for Planar One Degree-of-freedom Linkages, Demonstrated up to 8-Bar[J]. Journal of Mechanisms and Robotics, 2015, 7(1): 011006.

[10]杨廷力. 机械系统基本理论——结构学·运动学·动力学[M]. 北京: 机械工业出版社, 1996.

[11]徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社, 2002.

[12]CHEN G M, LIU X Y, DU Y L. Elliptical-arc-fillet Flexure Hinges: Toward a Generalized Model for Commonly Used Flexure Hinges[J]. Journal of Mechanical Design, 2011, 133(8): 602-610.

(编辑：王 瑞)

Automatically generating kinetostatic model for planar flexure-based compliant mechanisms

LIJiajie，LIUXiaoyuan，CHENGuimin

(School of Mechano-electronic Engineering, Xidian Univ., Xi’an 710071, China)

Based on the concept of graph theory, a new two-colored digraph representation of planar flexure-based compliant mechanisms is presented, which is mapped to computers by the data structure of the orthogonal list. Then, the vertices and edges of the diagraph are traversed in the order of operations, to automatically generate kinetostatic models for planar flexure-based compliant mechanisms. The process of the automatically generating kinetostatic model for planar flexure-based compliant mechanisms based on graph theory is illustrated by applying it to the differential micro-displacement amplification mechanism. The results achieved by the automatically generating model and the finite element method are in good agreement, which validates the effectiveness of the proposed methods.

planar flexure-based compliant mechanisms;graph theory;automatic generation

2015-11-10

时间：2016-04-01

国家自然科学基金资助项目(51175396)；中央高校基本科研业务费专项资金资助项目(K5051204021，xjs15041)；陕西省科技统筹资助项目(2014KTCQ01-27)

李佳杰(1986-)，女，西安电子科技大学博士研究生，E-mail：lijiajie1987@163.com.

陈贵敏(1978-)，男，教授，E-mail：guimin.chen@gmail.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.026.html

10.3969/j.issn.1001-2400.2016.06.013

TH122

A

1001-2400(2016)06-0074-06