一种考虑通道噪声的极化SAR定标改进算法

张海瀛，李真芳，李锦伟，房 超

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)



一种考虑通道噪声的极化SAR定标改进算法

张海瀛，李真芳，李锦伟，房 超

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

在利用极化合成孔径雷达数据进行各项研究时，首先需要对极化合成孔径雷达数据进行标定．现有Ainsworth算法在利用分布目标估计交叉极化通道不平衡参数时，没有考虑交叉极化通道噪声的影响，这将影响该参数的估计稳健性．针对此种情况，提出了一种改进的Ainsworth定标算法．该改进算法充分考虑了交叉极化通道噪声对交叉极化通道不平衡参数估计的影响，在交叉极化通道噪声不一致以及低信噪比的情况下具有良好的性能．基于仿真数据和实测数据的实验结果验证了该改进算法的有效性．

极化合成孔径雷达;极化定标;Ainsworth算法

极化合成孔径雷达(Polarimetric Synthetic Aperture Radar，PolSAR)遥感已经在地物分类以及植被参数估计等方面得到广泛的研究和应用[1-2]．在实际应用中，所有的极化分析与应用均需建立在各极化通道间的相对幅度和相对相位已进行精确标定的前提下，因而在利用极化合成孔径雷达(Synthetic Aperture Radar，SAR)数据进行各应用研究时，首要，需要校正由系统性能不理想引起的极化数据的畸变．目前，国内外众多学者已提出了大量的极化定标算法及其改进算法，主要包括使用点目标、使用分布目标[3]及混合使用点目标和分布目标[4-8]等3类定标算法，其中，混合使用分布目标和点目标的定标算法对极化系统和分布目标进行了一定的假设，简化了定标过程，因而该类算法在实际中得到了广泛应用．

由于目前的极化SAR系统可获得很高的极化隔离度，并能通过精确的内定标技术进一步提高极化数据的精度，因而，文献[6]提出了一种假设条件更加宽泛的定标算法——Ainsworth算法，其仅要求目标满足散射互易性，从而大大扩展了可用定标区域的选取范围，其已被成功应用于F-SAR系统[9]和无人机合成孔径雷达(Unmanned Aerial Vehicle Synthetic Aperture Radar，UAVSAR)系统[10]极化数据的标定．在实际应用中，现有Ainsworth算法在估计不平衡参数α的过程中并没有考虑交叉极化通道噪声的影响，因而当交叉极化通道噪声不可忽略时，参数α估计精度将会下降，从而导致极化数据的畸变无法被正确校正．为此，笔者提出了一种考虑交叉极化通道噪声的极化SAR定标改进算法，可消除交叉极化通道噪声对参数α估计的不良影响，提高参数α的估计精度．

1 极化定标模型

PolSAR定标算法的有效性与PolSAR系统模型的有效性紧密相关．观测的极化散射矩阵O与目标的真实散射矩阵S间的关系，可用PolSAR系统误差模型进行描述[5]，即

其中，R为接收失真矩阵，T为发射失真矩阵，N为系统加性噪声．式(1)中的矩阵均为 2×2 矩阵．式(1)可详细描述为

其中，下标H和V分别表示水平和垂直极化状态；SHV表示发射V极化、接收H极化时的回波，其余元素具有相似的含义．假设各极化通道噪声与信号不相关且各极化通道噪声间也不相关，则观测协方差矩阵Co和真实协方差矩阵Cs间的关系可表示为

其中，Co=o oH，Cs=s sH，Cn=n nH，[·]H表示共轭转置操作，·表示求集合平均，o为观测极化散射矢量，s为真实散射矢量，n为系统噪声矢量．各变量定义如下:

其中，k为接收通道不平衡参数，α为交叉极化通道不平衡参数，u、v、w和z为极化通道串扰参数，[·]T表示转置操作．通常情况下，参数Y和k的求取与参数u、v、w、z、α的求取可独立进行．Y和k参数的求取需要散射矩阵精确已知的先验目标，详细的描述可参考文献[4，8]．

2 改进的Ainsworth定标算法

Ainsworth极化定标方法仅仅要求场景中地物满足互易性，即SHV=SVH，并不要求场景中地物满足同极化通道和交叉极化通道间不相关的假设，即=0，i、j=h 或v，i≠j，从而扩大了定标区域的选取范围．由式(3)定义可得

当场景中的地物满足互易性时，矩阵D具有以下形式:

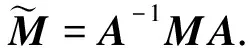
在实际应用中，Ainsworth算法通常忽略噪声项Cn，利用

α=(C33C22)1/2

实现参数α的估计，其中，Cxy表示矩阵C的xy项，下文中所有类似符号的含义与此处相同，arg(·)表示取相角操作．式(8)并没有考虑交叉通道噪声对参数α估计的影响．当交叉极化通道噪声的影响不可忽略，但在实际处理中不予考虑时，参数α的估计精度将受到影响．文中加性噪声被建模为零均值高斯白噪声[5]，即

在实际中，各极化通道的噪声功率可能并不相等，尤其对于H和V极化接收通道分置的系统，如相控阵型L波段合成孔径雷达(Phased Array type L-band Synthetic Aperture Radar，PALSAR)系统等，因而文中假定VH通道和HV通道的噪声功率比 m= N3/ N2．m值可利用符合一阶Bragg散射模型的光滑表面进行估计，一般平静的水面是最佳目标．为消除交叉极化通道噪声对参数α估计精度的影响，文中将Anisworth算法基本步骤中参数α的估计式(8)修改为[12]

式(10)在估计α时，不仅考虑了交叉极化通道存在噪声时的情况，而且还考虑了交叉极化通道噪声不一致的情况．改进的Anisworth定标算法的基本处理流程如下所述:

(1) 根据式(10)估计参数α的值．

(2) 计算矩阵A=diag(α，1，α，1)，并利用式(7)计算矩阵L．

(3) 利用式(11)估计G和H:

(4) 利用式(12)～(13)估计串扰参数u、v、w、z，即

其中，κ=[u，v，z，w]T，且有

(5) 利用步骤(1)中估计得到的α值、步骤(4)中估计得到的串扰参数及式(7)，完成矩阵D的估计．

因此，在忽略参数u、v、w、z的高阶项(二阶及以上)的情况下，可得转换后的噪声矩阵P中的元素为

因而在此步骤中需要按照

更新m值．

利用上述步骤可进行循环迭代，即将每次迭代估计得到的矩阵D作为下一次迭代的输入．如此循环迭代，直到迭代次数达到设定的次数或迭代过程中所有串扰参数的中间值低于设定阈值．根据文献[6，11]，在实验中，最大迭代次数设定为12，阈值设定为10-8．最终的参数估计值可由每次迭代的中间值(ui，vi，wi，zi，αi)给出，即

3 实验结果分析

为验证文中改进定标算法在精确估计参数α方面的有效性，分别利用仿真数据和德国Oberpfaffenhofen地区全极化数据对改进算法进行了实验分析．由于实际数据的失真矩阵不可能事先知道，因此，利用已标定好的全极化数据，通过设定失真参数值来产生实验数据．

真实协方差矩阵Cs中的元素被设置为代表植被的典型值[11]．在文中，主要分析交叉极化通道噪声对参数α的影响，以及改进算法对于α估计精度的提升性能．由于目前的极化雷达系统大都具有较高的极化隔离度，这意味着串扰参数均较小(幅度值小于0.1)，所以串扰参数对参数α估计精度的影响可忽略．文中将串扰参数u、v、w和z设置为固定值，如表1所示．参数α的幅度和相位分别在0.9～1.1和0～2π范围内选取．构造噪声矩阵Cn，使其具有diag(N，N/m，N，N)的形式，其中，N的取值范围为0.00～0.05，m的取值范围为0.5～2.0．

表1 仿真时串扰参数设置值

为分析改进算法估计参数α的性能随m值的变化情况，设定3个具有代表性的α值，其幅度值分别为0.9、1.0和1.1，相位均为 -70.08°，并设定 N= 0.05．图1表示的是m取不同值时参数α的估计值及估计误差．图1(a)为利用原始的Ainsworth算法估计得到的α幅度值，图1(d)为利用改进算法估计得到的幅度值．从图1(a)和图1(d)可以看出，原始Ainsworth算法的α幅度值的估计精度受交叉极化通道噪声影响明显，而改进后的算法对噪声表现了良好的鲁棒性，α幅度值的估计精度大大提高．从图1(c)可看出，当交叉通道噪声功率不一致时，原始算法对于α值的估计将会产生较大的误差，达到10-1数量级，而由图1(f)可看出，利用改进算法可大大提高α的估计精度，误差下降到10-3数量级．另外，从图1(b)和图1(e)可以看出，原始Ainsworth算法和改进算法对于α相位值的估计精度差异不大，误差均在 ±1° 之内．由于原始Ainsworth算法和改进算法对于α相位值的估计准确度均很高，因此，下面将主要在α的幅度值估计精度方面对改进定标算法的估计性能展开讨论．

图1 基于原始Ainsworth算法和改进算法的α估计值比较

为分析交叉极化通道信噪比对参数α估计精度的影响，分别将α和m的值设置为固定值1.1和0.5，而N的值由0.00到0.05均匀变化．文中分别利用原始Ainsworth算法和改进算法对参数α值进行估计．由于在上述设置下，HV通道的信噪比要低于VH通道的信噪比(参考噪声矩阵的形式)，因而仅画出α估计值以及其估计误差随HV通道信噪比的变化趋势，如图2所示．图2(a)为利用原始Ainsworth算法和改进算法估计得到的α幅度值随信噪比的变化，图2(b)为其估计误差随信噪比的变化．从图2可看出，当交叉极化通道信噪比较高时(此时对应低噪声水平)，原始Ainsworth算法可获得良好的α估计性能，但当信噪比降低时，估计精度明显降低．而改进算法的估计性能对信噪比的变化表现了良好的鲁棒性，低信噪比下估计误差仍然很小，因而改进算法对于参数α的估计性能要明显优于原始算法．

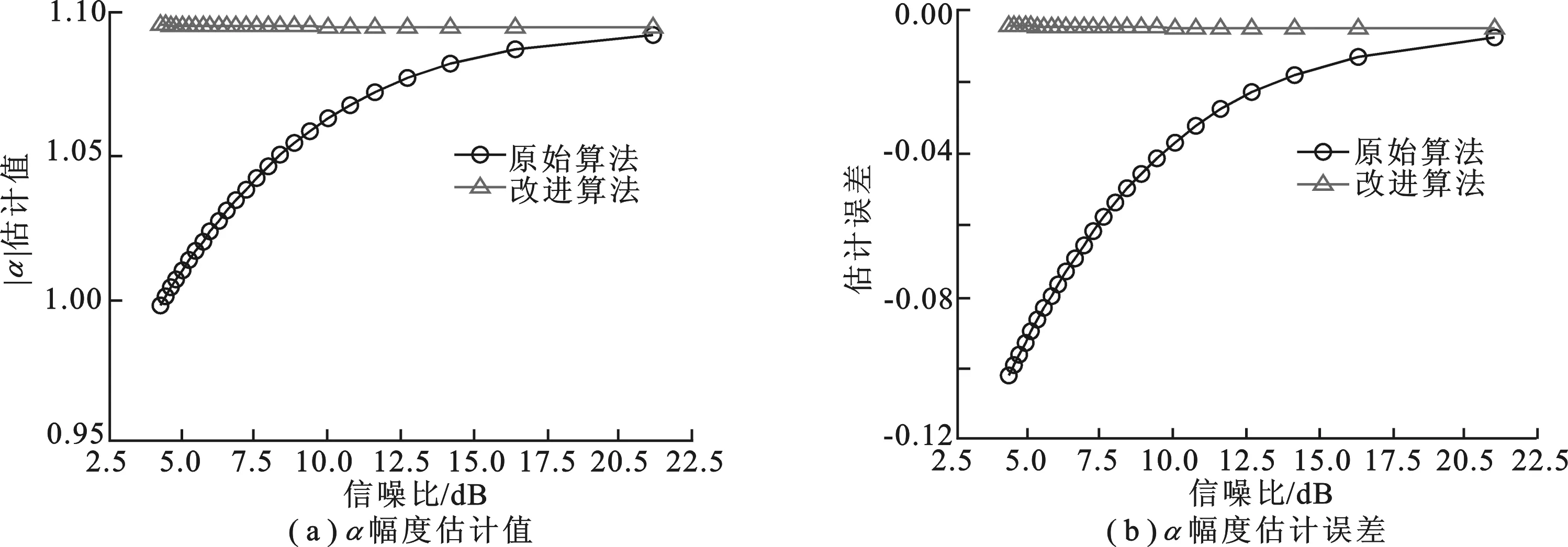
图2 α幅度估计值及其估计误差随信噪比的变化

为进一步验证改进定标算法的性能，利用德国Oberpfaffenhofen地区全极化数据，通过设定失真参数值和加性噪声值产生了一组实验数据．该数据中，串扰参数设置值仍然采用表1中所示的值，α值的幅度和相位值分别为1.1和 -70.08°，VH通道和HV通道的所加噪声的功率之比m取值为0.14．图3为基于该数据利用原始Ainsworth算法和改进算法估计得到的参数α的幅度和相位沿距离向的变化．从图3可看出，基于原始Ainsworth算法和改进算法的α的幅度和相位估计值随距离向均有所波动，这是由于实测数据中噪声沿距离向不均匀造成的．从图3(b)可看出，原始算法和改进算法在α相位值估计方面的性能基本相同，这与上面的分析结果相同．但值得注意的是，基于改进算法的α幅度估计值随距离向的波动明显比基于原始Ainsworth算法的小得多，如图3(a)所示，这说明改进算法的稳健性要明显优于原始算法．

图3 基于德国Oberpfaffenhofen地区全极化数据的α估计值随距离的变化

为更直观地说明改进算法的性能提升，这里给出了德国Oberpfaffenhofen地区全极化数据无失真时的合成图以及分别基于原始算法和改进算法失真参数估计值校正后的合成图，如图4所示．从图4中可看出，相比于原始算法，基于改进算法估计得到的失真参数校正后的合成图更接近于无失真时的合成图．

图4 德国Oberpfaffenhofen地区全极化数据合成图

4 结 束 语

现有Ainsworth算法在利用分布目标估计参数α时没有考虑交叉极化通道噪声的影响，当交叉极化通道噪声不可忽略时，参数α的估计精度将会明显降低．针对此种情况，文中提出了一种考虑交叉极化通道噪声的极化SAR定标改进算法．实验结果表明，该改进算法在交叉通道噪声功率不一致以及信噪比较低的情况下仍能保持良好的估计性能，从而可有效保证参数α的估计精度，实现极化SAR数据的精确标定，利于后续的极化分类等应用的研究．

[1] 刘璐, 王蓉芳, 焦李成, 等. 采用联合相似度谱聚类集成的极化SAR 分类[J]. 西安电子科技大学学报, 2015, 42(3): 48-53.

LIU Lu, WANG Rongfang, JIAO Licheng, et al. Combined Similarity Based Spectral Clustering Ensemble for POLSAR Classification[J]. Journal of Xidian University, 2015, 42(3): 48-53.

[2]卢红喜, 李东霖, 刘宏伟, 等. 双基线极化干涉SAR 植被参数反演[J]. 西安电子科技大学学报, 2015, 42(6): 23-29.

LU Hongxi, LI Donglin, LIU Hongwei, et al. Forest Parameters Retrieval with Dual-baseline Polarimetric SAR Interferometry Based on Clustering Analysis[J]. Journal of Xidian University, 2015, 42(6): 23-29.

[3]VILLA A, IANNINI L, GIUDICI D, et al. Calibration of SAR Polarimetric Images by Means of a Covariance Matching Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 674-686.

[4]VAN ZYL J J. Calibration of Polarimetric Radar Images Using Only Image Parameters and Trihedral Corner Reflector Responses[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(3): 337-348.

[5]QUEGAN S. A Unified Algorithm for Phase and Cross-talk Calibration of Polarimetric Data-theory and Observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(1): 89-99.

[6]AINSWORTH T L, FERRO-FAMIL L, LEE J S. Orientation Angle Preserving a Posteriori Polarimetric SAR Calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(4): 994-1003.

[7]ZHANG H, LU W, ZHANG B, et al. Improvement of Polarimetric SAR Calibration Based on the Ainsworth Algorithm for Chinese Airborne PolSAR Data[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 898-902.

[8]SHI L, YANG J, LI P. Co-polarization Channel Imbalance Determination by the Use of Bare Soil[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 95: 53-67.

[9]FISCHER J, BAUMGARTNER S V, REIGBER A, et al. Geometric, Radiometric, Polarimetric and Along-track Interferometric Calibration of the New F-SAR System of DLR in X-band [C]//2008 7th European Conference on Synthetic Aperture Radar. Frankfurt: VDE, 2008: 1-4.

[10]FORE A G, CHAPMAN B D, HAWKINS B P, et al. UAVSAR Polarimetric Calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3481-3491.

[11]GOH A S, PREISS M, Gray D A, et al. Comparison of Parameter Estimation Accuracy of Distributed-target Polarimetric Calibration Techniques[C]//International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2007: 4175-4178.

[12]KIMURA H, MIZUNO T, PAPATHANASSIOU K P, et al. Improvement of Polarimetric SAR Calibration Based on the Quegan Algorithm[C]//International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2004: 184-187.

(编辑：齐淑娟)

Improved polarimetric SAR calibration algorithm considering channel noise

ZHANGHaiying，LIZhenfang，LIJinwei，FANGChao

(National Key Lab. of Radar Signal Processing, Xidian Univ., Xi’an 710071, China)

It is necessary to calibrate polarimetric SAR(Synthetic Aperture Radar) data in order to use the data for scientific applications. The present Ainsworth algorithm does not consider the cross-polarization channel noise in estimating the cross-polarization imbalance parameter and therefore the estimation of this parameter is not robust. To solve the above problem, an improved Ainsworth algorithm is presented, which takes the cross-polarization channel noise into consideration. This algorithm can preserve a high performance under the situations of difference cross-polarization channel noise powers and a low signal noise ratio. Experimental results based on simulated and real data confirm the effectiveness of the improved algorithm.Key Words: polarimetric SAR;polarimetric calibration; Ainsworth algorithm

2015-10-25

时间：2016-04-01

国家自然科学基金资助项目(61471276，41371439)

张海瀛(1990-)，男，西安电子科技大学博士研究生，E-mail：zhanghaiying4155@163.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.016.html

10.3969/j.issn.1001-2400.2016.06.008

TN957

A

1001-2400(2016)06-0045-06