一种改进的多伯努利多目标跟踪算法

王海环，王 俊

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)



一种改进的多伯努利多目标跟踪算法

王海环，王 俊

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

针对粒子势均衡多目标多伯努利滤波的粒子实现形式所需粒子数多、粒子退化严重的问题，将均方根容积卡尔曼滤波与粒子势均衡多目标多伯努利滤波相结合，提出均方根容积卡尔曼粒子势均衡多目标多伯努利滤波算法．该算法利用均方根容积卡尔曼滤波构建重要性密度函数，再对其进行采样获得预测粒子状态，从而提高粒子的准确性，减轻粒子退化．与基于无迹卡尔曼的粒子势均衡多目标多伯努利滤波相比，该算法更稳定，且算法性能不受目标状态维数的限制．仿真实验表明，所提算法与粒子势均衡多目标多伯努利滤波算法和基于无迹卡尔曼的粒子势均衡多目标多伯努利滤波算法相比，其跟踪精度更高．

多目标跟踪;势均衡多伯努利滤波;粒子滤波;重要性密度函数;均方根容积卡尔曼滤波

近些年，基于随机有限集(Random Finite Sets，RFS)[1]的多目标跟踪算法开辟了多目标跟踪的一个新领域，此类算法的基本思想是对目标状态和观测量进行集合建模，将单目标贝叶斯滤波推广到多目标领域，从而避免了数据关联．此类算法的典型代表有概率假设密度(Probability Hypothesis Density， PHD)滤波[2]和势分布PHD(Cardinality PHD， CPHD)滤波[3]，其中，PHD滤波只传递全局后验概率密度的一阶矩，导致其在检测概率不为1时目标数目(即目标的势)估计误差较大；CPHD滤波同时传递一阶矩和目标的势分布，从而改善了PHD滤波的跟踪性能，但大大增加了算法的计算量．除PHD和CPHD滤波外，文献[4]提出了多目标多伯努利(Multi-target Multi-Bernoulli，MeMBer)滤波算法，其跟踪性能优于PHD滤波，而计算量小于CPHD滤波．文献[5]针对MeMBer滤波中目标数目过估计的问题，提出了势均衡多目标多伯努利(Cardinality-Balanced Multi-target Multi-Bernoulli， CBMeMBer)算法，进一步改善了MeMBer的跟踪性能．CBMeMBer的粒子实现形式(Particle CBMeMBer， P-CBMeMBer)不受线性高斯前提的限制，其适用范围更广，且P-CBMeMBer不需要通过聚类分析来实现目标状态的提取，从而降低了算法运算量，同时目标状态的获取不再依赖于估计的目标数目，因而更可靠．

P-CBMeMBer算法中直接利用目标状态转移方程产生预测粒子状态，导致粒子退化严重．为使预测粒子状态分布更接近于目标真实后验概率分布，常用的方法是在预测时引入当前时刻的观测量，对预测粒子状态进行修正，例如利用卡尔曼滤波(Kalman Filter， KF)或利用扩展卡尔曼滤波(Extent Kalman Filter，EKF)产生重要性密度函数，文献[6]提出基于无迹卡尔曼滤波(Unscented Kalman Filter，UKF)的P-CBMeMBer(Unscented Kalman Particle CBMeMBer， UP-CBMeMBer)算法，该算法利用UKF产生重要性密度函数，但UKF稳定性差，且算法性能受目标状态维数的影响．均方根容积卡尔曼滤波(Square-rooted Cubature Kalman Filter， SCKF)是基于球面-径向容积准则，以数值积分的方式来解决贝叶斯递推式中积分问题的一种非线性滤波方法[7]．同UKF相比，SCKF算法不需要进行矩阵开方运算，稳定性好，计算量小，且在目标状态维数较高时，其滤波性能优于UKF．因此，笔者采用SCKF算法构建P-CBMeMBer中的重要性采样函数，提出了均方根容积卡尔曼粒子CBMeMBer(Square-rooted Cubature Kalman P-CBMeMBer， SCP-CBMeMBer)滤波算法．该算法在P-CBMeMBer算法基础上引入了SCKF算法的优点．仿真实验表明，SCP-CBMeMBer算法与P-CBMeMBer算法和UP-CBMeMBer算法相比，其跟踪精度更高，稳定性更好．

1 背景知识

1.1 多目标贝叶斯滤波

RFS是数量有限的随机元所组成的集合，多目标跟踪中的目标状态集合和观测量集合可以分别看成两个RFS．设k时刻有N(k)个目标状态分别为xk，1，…，xk，N(k)的目标，有M(k)个状态分别为zk，1，…，zk，M(k)的观测量，基于RFS理论[8]，分别对多目标的目标状态集Xk和观测集Zk建模如下:

其中，N(χ)和N(ζ)分别为目标状态空间 χ⊆ Rnx和观测空间 N⊆ Rnz上所有有限子集的集合．

通过以上目标状态和观测量的RFS建模，可将单目标贝叶斯滤波推广到多目标跟踪中，得到多目标贝叶斯递推式为

其中，gk(·|·)为多目标联合似然函数，pk|k(Xk|Z1:k)为多目标联合后验概率密度，pk|k-1(Xk|Z1:k-1)为多目标联合先验概率密度，fk|k-1(Xk|Xk-1)为多目标状态转移概率密度函数．

1.2 CBMeMBer滤波

MeMBer滤波利用多个伯努利分量来近似多目标后验概率密度，滤波过程中通过传递各个伯努利分量的参数来估计当前时刻目标个数和各个目标的状态． 文献[5]指出，MeMBer滤波存在目标数目过估计，并对其进行改进，提出了CBMeMBer滤波，其实现过程如下:

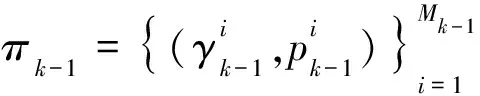
其中，

上式中，φk，z(x)=gk(z|x)pd，k(x)，gk(z|x)为单目标似然函数，pd，k(x)为检测概率，kk(z)为杂波概率密度函数．

2 改进算法

2.1 SCKF滤波

同UKF相似，SCKF也是一种通过数值积分来近似得到贝叶斯滤波中的高维积分的方法． 不同的是，SCKF是基于三阶球面-径向容积准则选取容积点，而UKF则是通过无轨迹变换(Unscented Transformation，UT)选取Sigma点． 文献[9]提出在高斯假设条件下，非线性滤波问题可转化成求解非线性函数乘以高斯概率密度的积分问题．考虑最简单的形式，则有

U(f)=∫Rnf(x) exp(-xTx)

SCKF首先通过坐标系转换得到与式(5)在球面-径向坐标系下的表示形式，再用数量不同的数值点分别近似球面积分和径向积分[10]，进而得到式(5)的近似式为

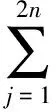
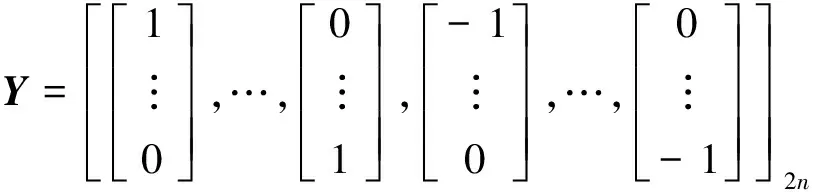
由以上分析可以看出，SCKF中容积点的个数比UKF中Sigma点的个数要少，且其对应权值的计算比UKF简单．因此，SCKF的计算复杂度要低于UKF的．同时，SCKF的性能不依赖于参数的选择，且不需要进行开方运算，算法稳定性更好．

2.2 SCP-CBMeMBer滤波

设目标的状态方程和观测方程为

其中，uk-1和vk分别为过程噪声和观测噪声，服从均值为0、协方差分别为Qk-1、Rk的高斯分布．

(1)预测．分别对存活伯努利分量和新生伯努利分量的重要性密度函数进行采样，得到k时刻的粒子状态和粒子权值为

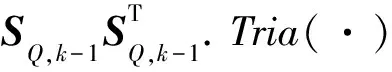
由预测粒子状态及其权值，可得到预测后验概率密度所对应的多伯努利参数集:

，

其中,

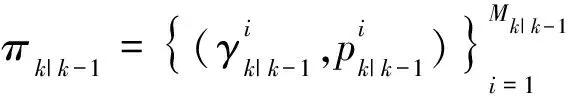
其中,

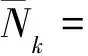
图1 目标真实轨迹

3 实验仿真

为验证SCP-CBMeMBer算法的性能，在杂波环境下，分别用P-CBMeMBer、UP-CBMeMBer和SCP-CBMeMBer这3种算法对数目时变的多个目标进行跟踪．

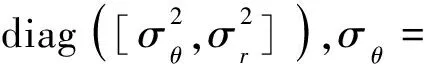
设目标出现的时刻分别为初始时刻、10 s、30 s和50 s，目标消失的时刻分别为 60 s、80 s、100 s 和 100 s，目标存活概率 ps= 0.98，检测概率 pd= 0.9，新生目标存在概率 γτ= 0.02，杂波在观测区域内均匀分布，每帧平均杂波数 λ=10，每条航迹最大采样粒子数 Lmax= 500，最少采样粒子数 Lmin= 100，最大航迹数目为100．

文中选取最优子模式分配(Optimal Sub-Pattern Assignment， OSPA)作为多目标跟踪精度评估标准[11]，仿真中取距离误差敏感参数 p=2，势误差敏感参数 c=500．图2和图3分别为100次蒙特卡罗仿真后，3种算法的势估计及其误差对比图和OSPA距离误差对比图．可以看出，SCP-CBMeMBer算法和UP-CBMeMBer算法的滤波精度无论在势估计还是在目标状态估计方面都远远优于P-CBMeMBer算法的，同时，由图2和图3可更加直观地看出，SCP-CBMeMBer算法的跟踪精度要优于UP-CBMeMBer算法的．这直观地说明，在目标状态维数较高时，SCP-CBMeMBer算法的性能优于UP-CBMeMBer算法的，与理论分析相符．

图2 势估计及其误差对比图图3 OSPA距离对比图

图4和图5为不同检测概率下，3种算法的势估计误差对比图和OSPA距离误差对比图．由图6和图7可以看出，随着检测概率的增大，3种算法的性能都有所提升，且相同检测概率下SCP-CBMeMBer算法的跟踪精度要优于P-CBMeMBer算法和UP-CBMeMBer算法的．

图4 势估计误差对比图图5 OSPA距离对比图

4 结 束 语

为在保证算法跟踪性能的前提下，减少P-CBMeMBer算法所需的粒子数，将SCKF滤波与CBMeMBer相结合，利用SCKF产生重要性密度函数，文中提出了SCP-CBMeMBer滤波算法．该算法能有效减轻P-CBMeMBer算法中的粒子退化，与UP-CBMeMBer算法相比，其计算量更小，且算法性能不受目标状态维数的影响，其适应性和稳定性更好．值得注意的是，CBMeMBer算法对每个观测量产生一条航迹，在杂波密度较大时，计算量很大，如何将概率数据关联与CBMeMBer算法相结合，减少杂波所增加的计算量是今后需要开展的工作．

[1] MAHLER R P S. Multitarget Bayes Filtering via First-order Multitarget Moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[2]李翠芸, 江舟, 李斌, 等. 未知杂波环境的GM-PHD平滑滤波器[J]. 西安电子科技大学学报, 2015, 42(5): 98-104.

LI Cuiyun, JIANG Zhou, LI Bin, et al. Gaussian Mixture PHD Smoothing Filter in Unknown Clutter[J]. Journal of Xidian University, 2015, 42(5): 98-104.

[3]VO B T, VO B N, CANTONI A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.

[4]MAHLER R P S. Statistical Multisource-multitarget Information Fusion[M]. Norwood: Artech House, 2007.

[5]VO B T, VO B N, CANTONI A. The Cardinality Balanced Multi-target Multi-Bernoulli Filter and Its Implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409-423.

[6]QIU H, HUANG G, GAO J. Unscented Particle Implementation of Cardinality Balanced Multi-target Multi-Bernoulli Filter[C]//Proceedings of the 2014 7th International Congress on Image and Signal Processing. Piscataway: IEEE 2014: 1162-1166.

[7]WANASINGHE T R, MANN G K I, GOSINE R G. Stability Analysis of the Discrete-time Cubature Kalman Filter [C]//Proceedings of the 2015 54th IEEE Conference on Decision and Control. Piscataway: IEEE, 2015: 5031-5036.

[8]VO B T, SEE C M, MA N, et al Multi-sensor Joint Detection and Tracking with the Bernoulli Filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1358-1402.

[9]ARASARATNAM I, HYKIN S. Cubature Kalman Filter [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[10]FENG Y L, YANG Q A, WANG S Y. Novel Cubature Kalman Filters Based Mixed Degrees [C]//Proceedings of the 6th International Conference on Intelligent Control and Information Processing. Piscataway: IEEE, 2015: 220-224.

[11]GOSTAR A K, HOSEINNEZHAD R, BAB-HADIASHAR A. OSPA-based Sensor Control [C]//Proceedings of the 4th International Conference on Control, Automation and Information Sciences. Piscataway: IEEE, 2015: 214-218.

(编辑：齐淑娟)

Multi-target tracking with the cubature Kalman multi-bernoulli filter

WANGHaihuan，WANGJun

(National Key Lab. of Radar Signal Processing, Xidian Univ., Xi’an 710071, China)

The particle cardinality-balanced multi-target multi-bernoulli(P-CBMeMBer) filter needs large numbers of particles and has serious particles degradation. To solve this problem, we combine the square-rooted cubature Kalman filter(SCKF) with the P-CBMeMBer filter, called square-rooted cubature Kalman P-CBMeMBer(SCP-CBMeMBer) filter. The SCP-CBMeMBer filter obtains the predicted particles by sampling the importance density function generated by the SCKF in order to alleviate particles degradation. Compared to the P-CBMeMBer filter based on the unscented Kalman filter(UP-CBMeMBer), the proposed method is more stable and its performance is unrestricted by the dimension of the target states. The results show that the proposed method has a higher accuracy than the P-CBMeMBer filter and the UP-CBMeMBer filter.Key Words: multi-target tracking; cardinality-balanced multi-bernoulli filter; particle filter; importance density function; square-rooted cubature Kalman filter

2016-05-23

国家自然科学基金资助项目(61401526)

王海环(1987-)，女，西安电子科技大学博士研究生，E-mail: haihuanwang@126.com．

10.3969/j.issn.1001-2400.2016.06.030

TN953

A

1001-2400(2016)06-0176-07