TDOA中的修正牛顿及泰勒级数方法

房嘉奇，冯大政，李 进

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)



TDOA中的修正牛顿及泰勒级数方法

房嘉奇，冯大政，李 进

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

在多站无源时差定位系统模型下，泰勒级数算法和牛顿算法在较差初始值条件下容易出现迭代发散问题．针对这一问题，提出了基于修正泰勒级数法和牛顿法的时差定位算法．该方法对于较差初始值引起的病态海森矩阵，运用正则化理论中的吉洪诺夫法或衰减奇异值分解法进行修正，其中控制海森矩阵修正量的重要的正则化参数由著名的L曲线理论确定．实验结果证明:相对于原泰勒级数及牛顿算法，经过改进后的算法对于较差的初始值，具有较高的概率使迭代算法的解稳健地收敛到目标的真实位置，并拥有较强的能力移除局部最小值;相对于时差定位模型下的一些广泛应用的线性解法，也成为闭式解法，在低信噪比环境下具有更高的定位精度．

无源定位;时差定位;修正泰勒级数算法;修正牛顿算法;正则化算法

多站无源定位技术是电子侦查、电子对抗的一个重要组成部分，被广泛应用于雷达、导航、监督、无线通信、无线传感器网络等领域．无源定位技术在测量参数方面可以分成接收信号强度(Received Signal Strength，RSS)、到达时间(Time Of Arrival，TOA)、到达角度(Angle Of Arrival，AOA)、到达时间差(Time Difference Of Arrival，TDOA)、到达频差(Frequency Difference Of Arrival，FDOA)等方法．笔者主要研究的是到达时间差方法，也称为时差定位技术．在三维空间中，该技术利用目标辐射源到两个接收基站的到达时间差信息确定一个以两基站为焦点的双曲面，通过多个基站的时差测量值确定多个双曲面，其交点即为目标位置．到达时间差目标位置估计方法有以下优点:接收机上通常只需安装单个天线；接收机与接收机之间不需要进行时间同步；定位精度较高．

由于基于到达时间差的定位问题高度非线性非凸特征，并不是一个能够简单求解的问题．到达时间差定位方法按照类型可以分为线性化方法和非线性化方法．目前大多数研究主要侧重于线性化方法(闭式解方法)[1-4]，这些方法通过线性化到达时间差的非线性方程组来求解目标位置，它们可被归类为线性最小二乘(Least Squares， LS)、两次加权最小二乘(Two-Stage Weighted Least Squares， TSWLS) 和多维尺度分析(MultiDimensional Scaling analysis，MDS) 等．线性化方法的特点是计算量小，在信噪比较高时定位精度能够达到克拉美罗界(Cramer-Rao Lower Bound， CRLB)，但线性化非线性方程组必然会带来性能的损失．因此，所有的线性化算法都会受到门槛效应的影响，即在噪声功率大到一定界限后定位精度误差逐渐偏离克拉美罗界．针对这一缺点，线性化算法所求得的解可以被作为非线性迭代算法的初值，从而去获取一个更精确的位置解．当前主要的迭代算法有泰勒级数法(Taylor-Series， TS)[5]以及牛顿法(NewTon， NT)[6]两种，但是迭代算法的一个重要弊端在于，当迭代初始值较差时(由线性化算法的解在大噪声环境下产生的较大偏差引起)，迭代算法很容易发散．

笔者将研究的重点放在解决迭代算法中最关键的收敛性问题上，利用最大似然估计(Maximum Likelihood， ML)确定目标函数，然后采用牛顿法进行求解．牛顿法是泰勒展开式的二阶近似，它忽略了泰勒展开式中的高阶项，然而在高度非线性的时差定位问题中，较差的初始值会导致高阶项对解的贡献变得比较重要，因而忽略高阶项很容易致使迭代发散．笔者提出了修正牛顿算法(Modified NewTon， MNT)用于克服该问题，对于由较差初值引起的病态海森矩阵，运用正则化理论中常用的吉洪诺夫(TIkhonov，TI)法或衰减奇异值分解法(Damped Singular Value Decomposition， DSVD)[7]将该病态矩阵转化为良态矩阵，其中控制海森矩阵修正量的重要的正则化参数由著名的L曲线理论[8]确定，并将其同另一种确定正则化参数的方法——广义交叉检验法(Generalized Cross Validation， GCV)进行对比．需要注意的是，泰勒级数算法相比较于牛顿算法只用到了一阶泰勒展开，因此正则化理论也可以应用到泰勒级数算法中．笔者同时提出了修正泰勒级数法(Modified Taylor-Series， MTS)对原泰勒级数算法进行改进．经过改进的修正泰勒级数法、修正牛顿算法同改进前的算法相比，在收敛性上具有稳定性，具有较好的移除局部最小值的能力，能够稳健地收敛到全局最优点; 同改进前算法和线性化算法相比，在低信噪比环境下具有更高的定位精度．

1 到达时间差定位模型

在多站无源时差定位系统下，假设待测目标辐射源位置x=[x，y，z]T，第i个已知接收基站的位置 si= [xi，yi，zi]T，i=1，…，M，M为参与定位的基站数目，在三维空间内至少需要4个不在同一平面之内的基站来确定目标的位置．目标和第i个基站之间的距离为

其中，·表示2范数．选定中心基站为第1个基站，则基站1和基站i之间的时差信息测量值为

其中，c为电磁波传播速度，ti1为基站1与基站i之间的到达时间差测量值，di1为与测量时差信息对应的测量距离差(Range Difference Of Arrival， RDOA)，ni1c为到达时间差测量误差．用测量距离差来代替到达时间差．将到达时间差测量等式方程组采用向量形式表达，即

其中，d=[d21，d31，…，dM1]T，r=[r1，r2,…，rM]T，n=[n21，n31，…，nM1]T．G为第1列均为 -1 的 (M- 1)×1 的列向量与维数为 (M-1) 的单位矩阵所合并的 (M-1)× M的矩阵，G= [-1M-1，IM-1]．噪声n为零均值、协方差矩阵 E(n nT)= Qt的向量．根据最大似然估计，目标函数可写为

2 牛顿法及修正牛顿法

牛顿法和泰勒级数法的本质相同，泰勒级数法只比牛顿法少用到了泰勒展开式中的二阶展开项．因此，首先研究牛顿法，去除二阶项即可得到泰勒级数法．牛顿法是一种经典的迭代算法，在每次迭代中通过二阶泰勒近似来改进估计值．令迭代次数 k=1，2，…，n，每次迭代后新的更新的估计值xk+1可表示为

xk+1=xk+Δxk=xk-2f(xk)-1

其中,

式(10)中的⊗表示Kronecker积，vec(·)表示将矩阵沿列向量化．文献[9-10]中分析了海森矩阵病态的原因并提出了正则化理论解决办法，在此基础上，笔者不仅仅对牛顿法，也对泰勒级数法进行了改进，并同时对正则化的方法以及正则化参数的选择进行了更深入的研究．令 A=2f(x)，b= -f(x)，矩阵A奇异值分解为

其中，U和V为单位正交矩阵，UTU=VTV=In，Σ=diag(σ1，σ2，…，σn)，σi和向量ui，vi为特征值和特征向量．由式(5)得到每次迭代的改变量

式(7)中的第2项即式(10)为二阶项．若忽略二阶项，牛顿法退化为泰勒级数法，因此只需将式(7)中第2项忽略，其他计算步骤不变，可在原泰勒级数法的基础上得到修正的泰勒级数法．其表达式可与牛顿法写成相同的形式，即式(5)～(7)，只需将式(7)中的第2项删去即可．

3 正则化理论

3.1 正则化方法

正则化理论是一种解决不适定问题的有效方法，它用一种与原不适定问题相邻近的适定问题的解去逼近原问题的解．常用的正则化方法有吉洪诺夫正则化法、截断奇异值分解法(Truncated Singular Value Decomposition，TSVD)和衰减奇异值分解法等．吉洪诺夫法正则化等价于求解式(13)在二次约束下的惟一最小二乘解，即将该问题转化为求解下述二次优化问题:

经过修正后的修正量为

经过修正后的改变量ΔxTI，其实质相当于在原参量前加入了滤波器fi．特征值越小，滤波器fi也越小，其小特征值对应项的贡献也越小．其中λ为正则化参数，用来控制式(14)中前项(数据能量)与后项(稳定能量)之间的比例．

截断奇异值分解方法仅采用矩阵A的大特征值对应的特征空间来构造方程组的解，舍弃了小特征值对应的特征向量．假设A有m个大特征值，则选取m作为截断参数．满足条件σ1，σ2，…，σm≥ λ的特征值保留，舍弃σ1，σ2，…，σm< λ的特征值．因此，采用截断奇异值分解法得到的修正量可以写为

衰减奇异值法就是常用的对角加载法，它是一种常用的稳健技术，可以有效地解决病态矩阵求逆问题．对式(13)直接应用对角加载，得到

这3种算法中截断奇异值分解法主要应用于区分信号和噪声空间的多特征值矩阵，而对于到达时间差目标定位问题，要求的海森矩阵在不考虑速度及基站误差的情况下维数很小，因此截断奇异值分解法这种直接滤除小特征值的方法对于本问题不适用．对于吉洪诺夫法和衰减奇异值分解法两种方法来说，吉洪诺夫方法适用于秩亏情况，而衰减奇异值分解法更适用于病态矩阵情况．

3.2 正则化参数

上节提到的3种方法的性能都十分依赖正则化参数λ的选择．正则化参数的选择方法有L曲线法和广义交叉检验法．L曲线理论将残差范数A Δx-b和正则化范数Δx的和作为变量取对数画图，通过对比结果确定正则化参数．该方法所绘制的尺度图形中会出现一条明显的L曲线．将曲线中的最大曲率作为其拐点，通过寻找该拐点求得与之相对应的λ．令 ρ= lg A Δx-b，θ= lg Δx，该曲率定义为

广义交叉检验法也是一种常用的确定正则化参数λ的方法，它的原理是假定将任意的观测值bi从原观测序列b中去除，在此时通过剩余观测值求得的正则化解能够较好地预测b中被去掉的这个观测值bi．它等效为求解下面函数的最小值问题:

矩阵Al满足关系式Δx=Alb．广义交叉检验法在理论上能够选择最优的参数λ，但某些时候广义交叉检验法函数的变化趋势非常平缓，这时很难找到它的最小值．而相比较而言，L曲线法能够快速准确地找到最佳正则化参数．因此，笔者采用L曲线法作为确定正则化参数的方法．

对一些值得注意的问题进行如下解释说明:

(1) 同泰勒级数算法相比，牛顿算法因为存在式(7)中的第2项，能够提供一个较为精确的海森矩阵，因此具有较高的定位精度．然而当初值较差时，牛顿算法中的海森矩阵可能负定导致迭代发散．对于泰勒级数算法，因为式(7)中的第1项一直为对称正定矩阵，因此具有较高的收敛概率，但因海森矩阵表达的不完全，其定位结果可能陷入局部最小值中．笔者提出的修正牛顿算法和修正泰勒级数算法继承了原算法的特点，相比于修正泰勒级数算法，修正牛顿算法具有较高的定位精度和较差的收敛性．

(2) 众所周知，迭代算法需要一个初值，它完全随机选取是不合适的．在实际应用中，闭合式算法的解通常被作为初值带入迭代算法．笔者采用著名的两次加权最小二乘算法来求得初值．在噪声较大时，两次加权最小二乘算法的解可能存在较大误差，此时多维尺度分析算法被用来取代两次加权最小二乘算法以获得一个误差相对较小的初值．

(3) 当目标函数值f(xk+1)>f(xk)时，认为迭代的过程中出现了发散的现象；反之，则认为迭代收敛，继续观察，并设定迭代的终止条件为梯度f(xk)< ε．由于时差定位问题的高度非线性特征，因此有时候尽管迭代收敛，但其结果可能陷入局部最小值中．当使用闭合式算法的解作为迭代算法的初值时，若迭代的最终结果为全局最优解，则迭代只需要非常少的次数就可以收敛; 若最终结果为局部最小值，则需要多次迭代才能收敛．在这里需要设定一个迭代次数的门限用来移除局部最小值．如果该门限设置较为宽松，则少量的局部最小解仍然存在于全局最优解中，致使平均值变差; 反之，如果该门限设置较严，则许多全局最优解将被遗弃，算法实用性降低．笔者提出的正则化算法通过对海森矩阵的修正，在实际上会减慢目标函数的收敛速度，对于全局最优解影响很小．而对于局部最小解来说，由于其本身收敛速度就较慢，再经过文中算法的减缓，收敛速度进一步降低，很容易就能够超出所设置的迭代门限．相对于文献[6]中所设置的较严格的两次迭代门限(超过两次迭代的结果都当做局部最小值被移除，会导致很多全局最优解的遗失)，笔者所设置的门限为较为宽松的5次．由于笔者提出的算法具有较强的辨识局部最小值的能力，因此在保证算法实用性的同时，又能够获得较好的性能．

4 仿真实验

实验中假设5个基站的位置分别为 (300 m，100 m，150 m)，(400 m，150 m，100 m)，(300 m，500 m，200 m)，(350 m，200 m，100 m)，(-100 m，-100 m，-100 m)，设置基站1为中心基站，近距离目标和远距离目标位置分别为 (280 m，325 m，275 m) 或 (2 800 m，3 250 m，2 750 m)．目标的定位精度以均方误差(Root Mean Square Error， RMSE)形式表示．实验中的测量距离差为零均值，协方差矩阵 σ2R 的高斯噪声，σ2为时差测量中噪声的功率，R为对角线元素为1而其余元素为0.5的矩阵，设置迭代次数门限为5．实验为 5 000 次蒙特卡罗实验的平均数据．

图1和图2描述了近距离和远距离目标情况下泰勒级数法、牛顿法、修正泰勒级数法和修正牛顿法的收敛概率值．从图中可以看到，根据说明(1)中的解释，泰勒级数法、修正泰勒级数算法在收敛性上相比于牛顿法，修正牛顿算法的更好．在图1中，泰勒级数法和牛顿算法随着噪声的变大，很容易导致迭代发散，而笔者所提出的修正泰勒级数法和修正牛顿算法具有较强的性能来保证迭代的收敛．在噪声较大时，收敛概率可以提高大概10%．在图2中，泰勒级数法、修正泰勒级数法和修正牛顿算法都具有较好的收敛概率，只有牛顿法的收敛性较差．

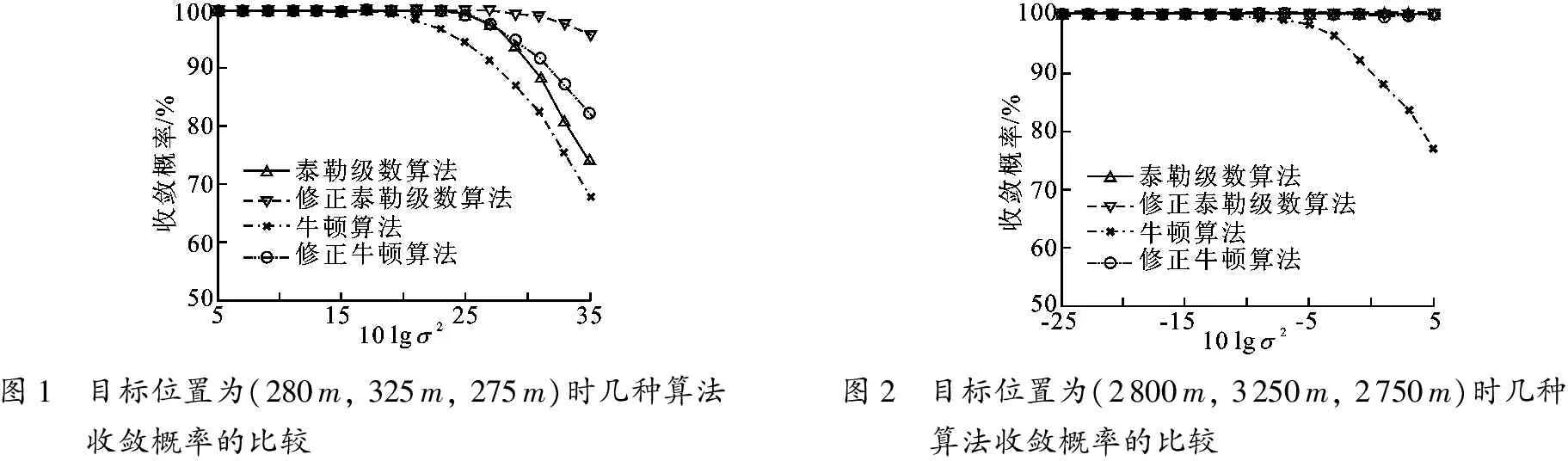
图1 目标位置为(280m，325m，275m)时几种算法收敛概率的比较 图2 目标位置为(2800m，3250m，2750m)时几种算法收敛概率的比较

图3和图4分别展现了近距离和远距离目标情况下泰勒级数法、牛顿法、 修正泰勒级数法和修正牛顿算法的定位精度估计，同时和两种经典的闭合式算法两次加权最小二乘和多维尺度分析进行比较．从图3可以看到，所有的算法在高信噪比时都能够达到克拉美罗界．随着噪声的提升，闭合式算法两次加权最小二乘、多维尺度分析受门槛效应的作用，所求的位置解误差逐渐变大; 泰勒级数法和牛顿算法的定位精度也严重地偏离了克拉美罗界，这是因为结果中存在的局部最小值大大提升了平均均方误差估计值．笔者提出的修正泰勒级数法、修正牛顿算法相比于其他算法在大噪声环境下具有较高的定位精度，从图中可以注意到，修正泰勒级数算法的定位精度相比于多维尺度分析算法的略差，这是因为在实验中设置的迭代次数门限较为宽松，致使结果中依然存在少量的局部最小值从而拉高了平均估计精度．门限选取越严格，修正泰勒级数法的估计精度越趋近于修正牛顿算法．在图4中可以看到，修正泰勒级数法和修正牛顿算法的定位精度优于其他算法的，由于式(7)中的第2项的值在远距离目标情况下会变得很小，因此笔者提出的两种算法结果趋于一致．定位精度在噪声非常大时略低于克拉美罗界，这是因为噪声过大时的估计不再是无偏估计的．

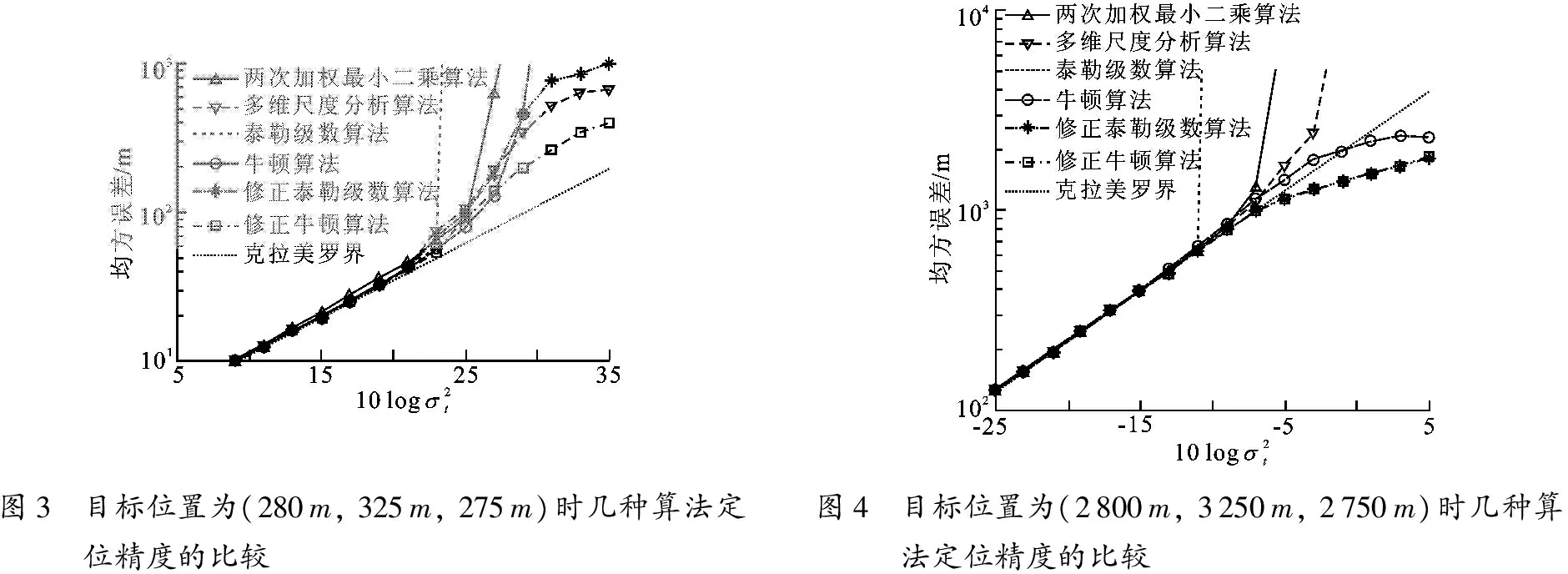
图3 目标位置为(280m，325m，275m)时几种算法定位精度的比较 图4 目标位置为(2800m，3250m，2750m)时几种算法定位精度的比较

图5给出了修正牛顿算法中的两种正则化算法——吉洪诺夫法、衰减奇异值分解法的比较结果，实验从均方误差和收敛概率两方面分别验证了算法的性能．由于初值由闭合式算法给出，相比于随机给出的初值更为准确．从图中可以看出，在定位精度方面，两种方法几乎相同；在收敛概率方面，吉洪诺夫算法的收敛性要略好于衰减奇异值分解算法的．

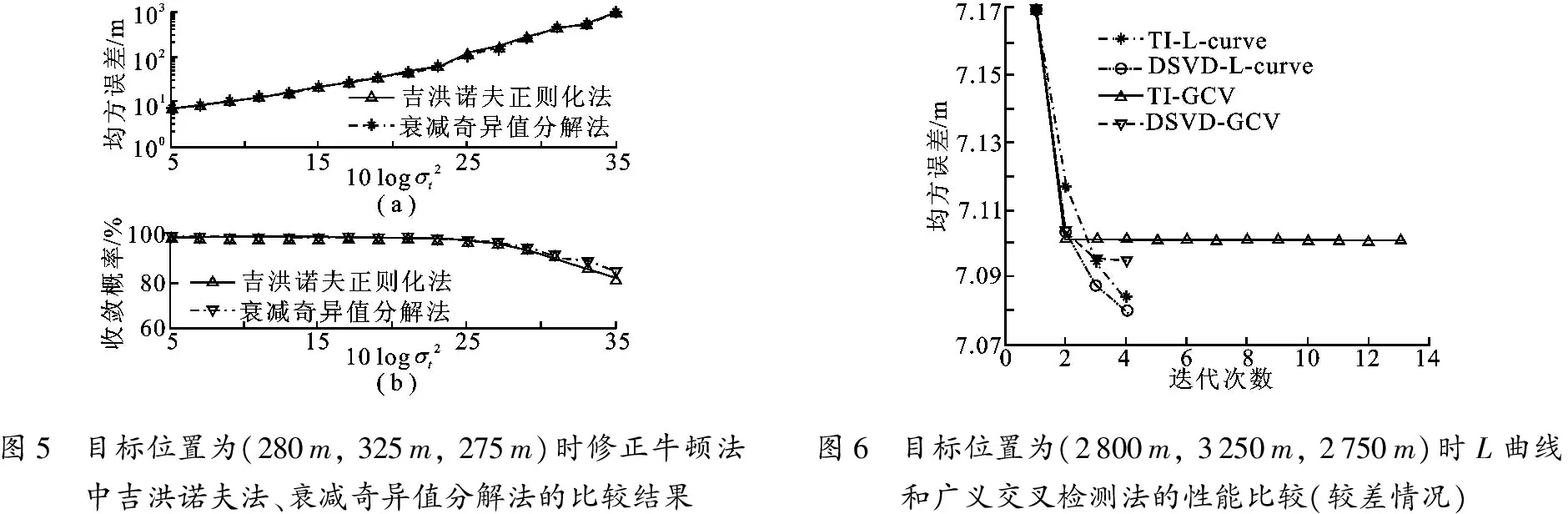
图5 目标位置为(280m，325m，275m)时修正牛顿法中吉洪诺夫法、衰减奇异值分解法的比较结果 图6 目标位置为(2800m，3250m，2750m)时L曲线和广义交叉检测法的性能比较(较差情况)

5 结 束 语

对到达时间差定位问题，笔者在原迭代算法基础上提出了修正泰勒级数法以及修正牛顿法，运用正则化理论中的吉洪诺夫技术修正病态海森矩阵，解决了迭代方法中关键的收敛性问题．同原方法相比，经过改进的修正泰勒级数法、修正牛顿算法能够更加稳健地收敛到全局最优解; 与两次加权最小二乘、多维尺度分析等线性算法相比，尽管由于迭代算法的特性使其计算量相对较大，但在低信噪比环境中定位误差更接近于克拉美罗界．文中算法的核心思想在于对病态海森矩阵的正则化处理，此算法可用于多种观测模型，如到达时间、到达角度等．当目标运动时，此算法也能够结合到达频差方程组求解目标的位置及速度，具有良好的实用价值和广泛的适用范围．

[1] WANG Y, HO K C. TDOA Source Localization in the Presence of Synchronization Clock Bias and Sensor Poition Erors[J]. IEEE Transactions on Signal Processing, 2013, 61(18): 4532-4544.

[2]WEI H W, PENG R, WAN Q, et al. Multidimensional Scaling Analysis for Passive Moving Target Localization with TDOA and FDOA Measurements[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1677-1688.

[3]LIN L, SO H C, CHAN F K W, et al. A New Constrained Weighted Least Squares Algorithm for TDOA-based Localization[J]. Signal Processing, 2013, 93(11): 2872-2878.

[4]朱国辉, 冯大政, 周延. 一种利用多运动接收站的时差定位算法[J]. 西安电子科技大学学报, 2015, 42(2): 35-39.

ZHU Guohui, FENG Dazheng, ZHOU Yan. New TDOA Localization Algorithm Using Multiple Moving Receivers[J]. Journal of Xidian University, 2015, 42(2): 35-39.

[5]KOVAVISARUCH L, HO K C. Modified Taylor-series Method for Source and Receiver Localization Using TDOA Measurements with Erroneous Receiver Positions[C]//Proceedings of the IEEE International Symposium on Circuits and Systems: 3. Piscataway: IEEE, 2005: 2295-2298.

[6]YU H, HUANG G, GAO J, et al. An Efficient Constrained Weighted Least Squares Algorithm for Moving Source Location Using TDOA and FDOA Measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 44-47.

[7]HANSEN P C. Regularization Tools: a Matlab Package for Analysis and Solution of Discrete Ill-posed Problems[J]. Numerical Algorithms, 1994, 6(1): 1-35.

[8]HANSEN P C, JENSEN T K, RODRIGUEZ G. An Adaptive Pruning Algorithm for the Discrete L-curve Criterion[J]. Journal of Computational and Applied Mathematics, 2007, 198(2): 483-492.

[9]房嘉奇, 冯大政, 李进. 稳健收敛的时差频差定位技术[J]. 电子与信息学报, 2015, 37(4):798-803.

FANG Jiaqi, FENG Dazheng, LI Jin. A Robustly Convergent Algorithm for Source Localization Using TDOA and FDOA[J]. Journal of Electronics & Information Technology, 2015, 37(4): 798-803.

[10]房嘉奇, 冯大政, 李进. 存在基站误差的稳健时差定位算法[J]. 系统工程与电子技术, 2015, 37(5):998-1003.

FANG Jiaqi, FENG Dazheng, LI Jin. Robust Source Location Algorithm Using TDOA in the Presence of Sensor Position Errors[J]. Systems Engineering and Electronics, 2015, 37(5): 998-1003.

(编辑：郭 华)

Research on modified Newton and Taylor-series methods in TDOA

FANGJiaqi，FENGDazheng，LIJin

(National Key Lab. of Radar Signal Processing, Xidian Univ., Xi’an 710071, China)

In the Time Difference Of Arrival (TDOA) source localization model, based on the Taylor-series (TS) method and Newton (NT) method, this paper presents the Modified Taylor-series(MTS) method and the Modified Newton method(MNT), which solve the critical convergent problem caused by the bad initial value in the original algorithms. The proposed algorithms modify the ill-condition Hessian matrix caused by the bad initial value using the Tikhonov (TI) or the Diagonal Singular Value Decomposition technique (DSVD) in the Regularization theory. The regularization parameter which controls the properties of the regularized solution is determined by the L-curve method. Simulation results show that compared with the TS and NT methods, the proposed methods ensure that the solution of the iterative methods converges on the source location, improves the convergent probability and has a better capability to remove the local minima. The proposed methods also give superior performances of the location accuracy comparing with the closed-form algorithms in low SNR environment.

source localization; time-difference-of-arrival; modified Taylor-series method; modified Newton method;regularization method

2015-10-11

时间：2016-04-01

国家自然科学基金资助项目(61271293)

房嘉奇(1984-)，男，西安电子科技大学博士研究生，E-mail: fangjiaqi123@hotmail.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.010.html

10.3969/j.issn.1001-2400.2016.06.005

TN97

A

1001-2400(2016)06-0027-07