基于匹配空间变换的群目标信号分离与重构*

王义哲,冯存前,李靖卿

(空军工程大学防空反导学院,西安 710051)



基于匹配空间变换的群目标信号分离与重构*

王义哲,冯存前,李靖卿

(空军工程大学防空反导学院,西安 710051)

针对窄带雷达获取的弹道中段群目标回波错综交叠、难以分离的问题,提出了一种基于匹配空间变换的群目标微多普勒特征提取方法。在构建群目标模型的基础上,利用自相关法提取出各子目标的微动周期,并结合微多普勒曲线变化规律,构造出对应的匹配空间。最后利用能量峰值搜索法结合CLEAN算法,依次估计出该子目标各散射点参数,并重构出回波信号。仿真结果表明,该方法能够克服背景噪声和信号混叠的影响,较好的实现了中段群目标的分辨。

群目标;微多普勒;匹配空间变换;时频分析

0 引言

弹道导弹在中段飞行持续时间较长且飞行轨迹易被确定和预测,所以中段被认为是弹道导弹防御中最关键的阶段[1]。然而中段防御也存在缺点,主要是诱饵释放等一些对抗措施迷惑防御系统。同时,母舱及助推器的残骸在近似真空的环境中伴随着弹头惯性飞行,形成扩散的目标群。这些目标具有相似的弹道特性[2],给真弹头的识别带来极大困难。因此,为了提取单个目标轨道参数与微动参数,必须对群目标回波信号进行分离。

针对群目标分离,文献[3]提出了一种基于欠定盲分离的多目标回波微多普勒特征分离方法,但该方法要求天线接收体制至少为3个,难以满足实际观测条件;文献[4]提出了一种基于时频滤波器的分离方法,利用逆时频变换提取各个信号分量,但该方法的性能受多个参数选择的影响;文献[5]利用Viterbi算法进行微多普勒提取,然后依据同一目标微动周期的相关性实现群目标的分离,但该方法对噪声过于敏感。

为了解决上述问题,文中提出了一种基于匹配空间变换的群目标信号分离与重构方法。首先求出各子目标的微动周期,再构造对应的匹配空间变换函数,然后对匹配空间域的能量分布进行峰值搜索,基于CLEAN算法依次提取并消去最强散射点,从而循环分离并估计出各子目标各散射点的微多普勒参数和散射系数,实现了各子目标回波信号的重构。

1 中段群目标模型构建与分析

在弹道中段,目标运动是沿弹道的平动与绕质心的微动二者的合成。为了分析简便,文中假设中段目标的平动已完全补偿。

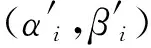
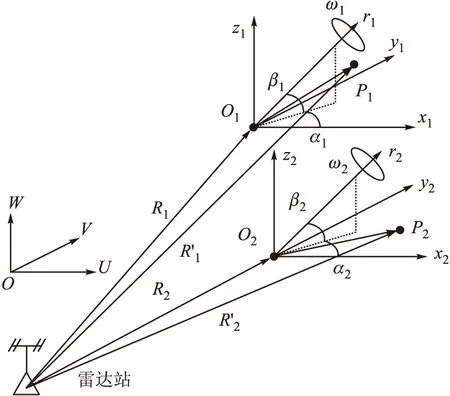
图1 群目标微动模型

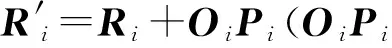
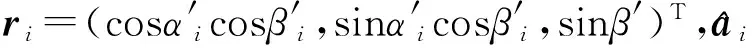
设雷达辐射的脉冲信号形式如下:

(2)

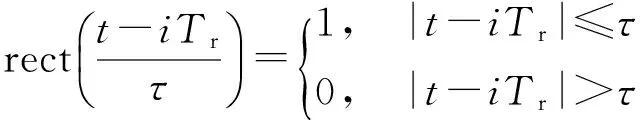
定义Tr为信号的脉冲重复周期,f为信号载频,τ为信号的脉冲宽度。

则经过雷达的正交双通道处理后,得到第i个旋转点基带回波信号如下:

(3)

式中:c为光速;σi为目标i的散射系数。对于单载频信号,如果忽略各散射点的散射强度受到目标微动影响所产生的改变时,即假设σi不变时,则目标回波信号为多分量调频信号,对其进行时频分析即可获得目标多普勒的变化规律。

当群目标中各子目标之间距离间隔小于雷达的距离分辨力时,包含L个散射点的群目标所在距离门的回波信号可分别表示为:

(4)

式中:ki为幅度调制因子;ωi为频率调制因子;θi为初相。ωi由目标微动的角频率决定,ki和θi由雷达波长、目标与雷达的相对位置和散射点分布决定。若能提取式(4)中的信号参数,即可估计出目标的微动参数。然而,文献[8]指出,即使是简单散射点微动模型之间的相互作用,也会给其微多普勒特征造成细微却不可忽略的影响,包括失真和畸变,尤其在时频交叠处影响更为恶劣。由式(3)、式(4)也可看出,群目标的回波信号不仅在时域上几乎完全混叠,而且在频域上各目标频率变化均具有周期性特点且中心频率均为零频,因此,单独从时域或频域对回波进行分离难以实现。

2 微动周期估计方法

由第2节分析可知,目标回波信号中包含σi、ki、ωi、θi四个参数。散射系数σi虽然不属于微多普勒参数,但作为一种目标特征,一定程度上暗示了目标散射点的位置分布情况和结构特征,因而也能作为一种潜在提高雷达系统识别能力的信息。为了降低未知参数维数,首先考虑估计微动周期得到ωi。

微动周期是重要的微动特征之一,目前国内已有不少相关成果。基于序列周期估计的方法主要有适用于单、多谐波信号和的最大似然估计法、谱估计法,以及适用于一般周期信号的自相关法、平均幅度差函数法等,后一类方法原理简单、计算量相对小,特别适合微动信号这种短时序列的周期估计。其中自相关法的应用最为广泛,基于此的微动周期估计表达式为[9]:

(5)

式中:Tmin与Tmax为微动周期的上限和下限,根据先验知识不难得到;Φ(m)为所处理序列的自相关函数。对中段群目标回波而言,s(t)中包含多个目标不同周期的回波信号,不同目标所对应微动周期相异,但同一目标各散射中心对应的微动周期一致,通过寻找信号自相关系数极大值点可提取各目标所对应的周期。

3 匹配空间变换

不考虑噪声时,群目标回波信号的离散形式为:

(6)

式中,N为信号长度,1≤n≤N。

对于s(n),定义子目标i的匹配空间变换函数M(k,θ)为:

(7)

式中,1≤k≤N,0≤θ≤2π。可见,匹配空间变换由微动角频率ωi和微多普勒的正弦调频形式这两个先验知识构成,有着明确的物理意义。

进一步求出,群目标回波信号在匹配空间域的能量分布W(k,θ)为:

W(k,θ)=|M(k,θ)|2=

(8)

将s(n)的表达式(6)代入式(7)中,可得群目标回波的匹配空间变换为:

(9)

为了得到匹配空间变换与原信号的关系,下面分两种情况讨论式(9)的值域分布。

当k=ki,θ=θi时[10]:

(10)

式中:m为整数;Jm(·)为第一类m阶贝塞尔函数:

(11)

不难看出,式(10)可化简为:

(12)

同理,当k≠ki,θ≠θi时:

(13)

式中:

(14)

因此,式(13)可化简为:

(15)

由此可知,M(ki,θi)>M(k,θ),即不同散射点在匹配空间域的能量分布W(k,θ)仅在(ki,θi)处有最大值,且该最大值远大于W(k,θ),(k,θ)≠(ki,θi),这样通过搜索峰值出现的位置即可估计出对应散射点的微多普勒参数。一般情况下,对应微动角频率ωi的子目标i的散射点不止一个,这时峰值数目与散射点数目相同,且幅度与ki成正比。由此得到的参数表达式为:

(16)

此外,比较式(12)、式(15)易得,M(k,θ)的值在(ki,θi)处及其邻域发生跳变,而在该区域之外的周围区域连续,峰值相对于最近周围连续区域的增量约为σiN,这样可得到散射点i的散射系数σi的估计为:

(17)

式中,绝对值内第二项为M(k,θ)在(ki,θi)处跳变区域之外的最近连续区域均值。发生跳变的原因可归结为只有参数匹配时,匹配空间中参数才能完全一致,能量达到最大,而失配时则只有个别非零点才有能量积累。

4 群目标分离与重构

实际考虑噪声存在的情况下,含有L个散射点的群目标回波信号为:

(18)

由于目标各散射点强度差异较大,对匹配空间变换域的能量分布进行峰值检测时,强散射点信号分量将淹没弱散射点信号分量。针对这一问题,采用基于消卷积的CLEAN算法思想[11],对数据进行搜索迭代时,依次消除最强散射点,并预先设定门限值作为推出循环的条件,当剩余结果最大值小于设置的门限时,循环结束。通过这种逐步消除,就可以降低强散射点信号分量的影响,实现弱散射点微多普勒参数的提取。

综合以上分析,弹道中段群目标分离与重构方法具体步骤如下:

1)通过自相关法估计子目标的个数及对应的微动周期得到ωi;

2)对回波信号s(n)进行匹配空间变换,得到M(k,θ);

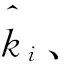
4)采用CLEAN算法消除最强散射点的能量,重复第3)步,直至剩余信号能量最大值低于预设门限;

5)重复上述步骤可得到各子目标各散射点的微多普勒参数和散射系数,即实现了群目标信号的分离与重构。

5 仿真分析

假设群目标中包含两个自旋目标,雷达载频为10 GHz,采样频率为2 kHz。目标1含有两个等效散射中心,坐标分别为(2,1.5,0)、(0,1.5,2.5),对应的旋转轴的视角为(65°,35°),自旋频率为f1=2.4 Hz;目标2也含有两个等效散射中心,坐标分别为(-1.2,2,0)、(1.6,0,1.2),对应的旋转轴的视角为(75°,65°),自旋频率为f2=3 Hz。两个目标的雷达观测视线均设为(45°,45°),且目标1和目标2所含散射点的散射系数为σ11∶σ12∶σ21∶σ22=4∶5∶2∶3。

假设信噪比SNR=0 dB,信号噪声为高斯白噪声。图2为经SVD去噪处理后的时频图,时频变换工具采用STFT,可以看出即使背景噪声得到了一定的抑制,依然存在错综复杂的时频曲线相互交叠、局部交叉区域发生畸变等现象,且弱散射点分量在强散射点的淹没下可见性又大大降低,导致难以从时频图中抽取各散射点的微多普勒特征。图3为回波信号在目标1的匹配空间域能量分布图,可以看出两处峰值分别对应目标1的两个散射点。图4(a)、图4(b)分别为采用文中分离重构方法依次提取出的目标1中两散射点的微多普勒信息,可以看出目标1的微多普勒特征得到了较好的还原。同样的,图4(c)、图4(d)为目标2中两散射点的重构微多普勒,弱散射点的特征也被完整而不失真的提取。此外,由于该方法避免了交叉区路域路径选择问题,也就减少了畸变现象的发生。

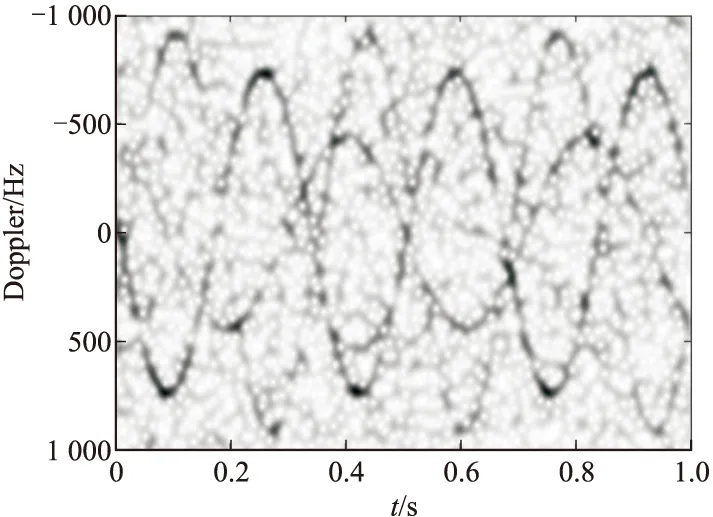
图2 SVD去噪后的时频分布

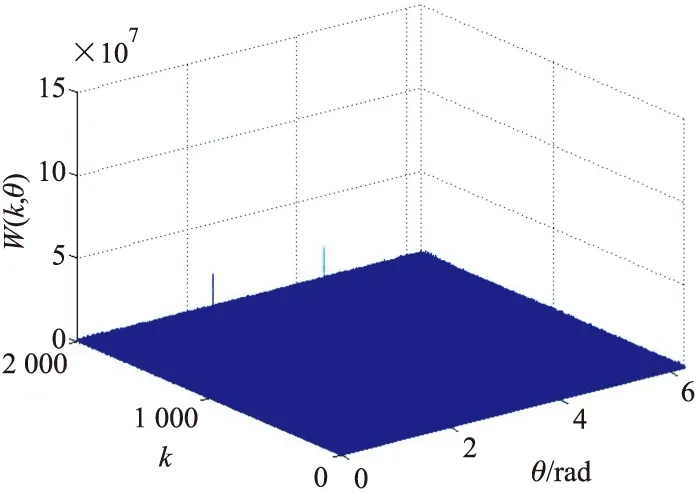
图3 目标1的匹配空间域能量分布

在上述条件下,进行100次蒙特卡罗仿真,目标1、2所含散射点的散射系数的估计结果如表1所示。分析参数性能时主要考察估计结果相对真值的相对误差(Relative Error,RE):

(19)

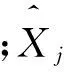
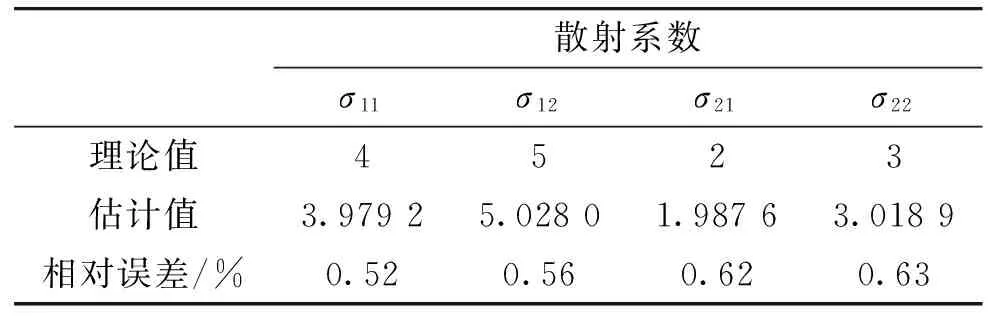
表1 SNR=0 dB时各散射点散射系数估计误差分析

为了进一步验证文中方法的准确性,在信噪比从-10dB到10dB变化时,对目标1的分离重构过程进行100次蒙特卡罗仿真,两散射点各个估计参数对应的相对误差如图5所示。可以看出,文中方法可同时较好的提取出强散射点和弱散射点的微多普勒,且受噪声影响较小,随着信噪比的增加,估计的相对误差逐渐稳定于定值,可以满足一定精度的需要。

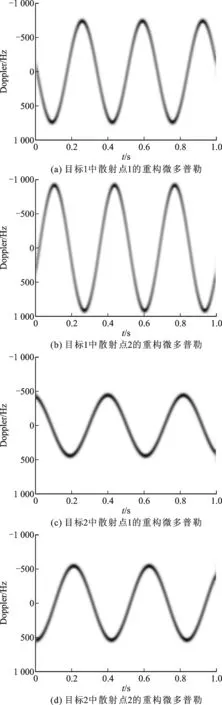
图4 群目标回波信号的重构微多普勒

6 结论

文中提出了一种抗噪性能好的群目标微多普勒特征和散射强度提取方法。利用自相关法估计出某一子目标的微动周期,并将该周期作为先验知识并结合微多普勒的正弦调频形式,构造出匹配变换空间,通过在该空间内进行能量峰值搜索,实现了目标微多普勒特征和散射强度的提取。该方法物理意义明确,适用于包括振动、旋转和锥旋在内的微动目标,且同时实现了微动特征和散射情况的提取,为群目标分辨提供了更多信息。在下一步研究中,将考虑微多普勒形式为非正弦调频的复杂微动形式,把该方法推广至此类群目标的识别应用中去。

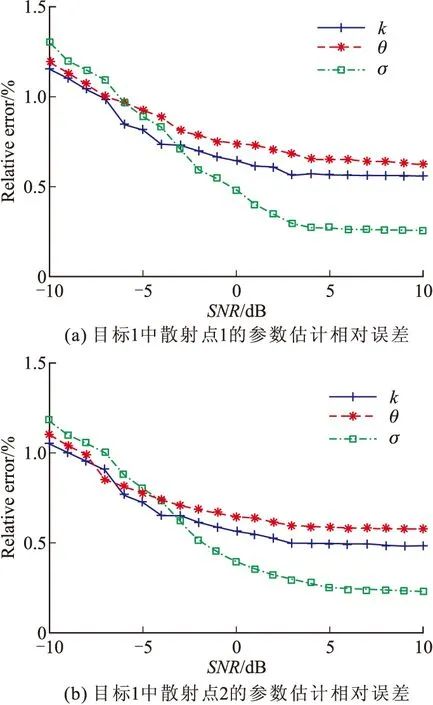
图5 不同信噪比下文中方法的参数估计误差分析

[1] UPENDRA Kumar Singh, VINEET Padmanabhan. Dynamic classification of ballistic missiles using neural networks and hidden Markov models [J]. Applied Soft Computing Journal, 2014, 19(1): 280-289.

[2] LIU Huo-Ping, WU Qin-Zhang, JI Ming-Gen, et al. Reentry optics extended group-target’s multi-mode detecting and tracking [J]. Contro Acta Photonica Sinica, 2013, 42(3): 336-341.

[3] 郭琨毅, 张永丽, 盛新庆, 等. 基于欠定盲分离的多目标微多普勒特征提取 [J]. 电波科学学报, 2012, 27(4): 691-695.

[4] LI Po, WANG De-Chun, WANG Lu. Separation of micro-doppler signals based on time frequency filter and Viterbi algorithm [J]. Signal, Image and Video Processing, 2013, 7(3): 593-605.

[5] 胡晓伟, 童宁宁, 董会旭. 弹道中段群目标平动补偿与分离方法 [J]. 电子与信息学报, 2015, 37(2): 291-296.

[6] 刘进, 马梁, 王雪松, 等. 微多普勒的参数化估计方法 [J]. 信号处理, 2009, 25(11): 1759-1765.

[7] CHEN V C, LI F Y, HO S S, et al. Micro-Doppler effect in radar: phenomenon, model and simulation study [J]. IEEE Trans. on Aerospace and Electronic Systems, 2006, 42(1): 2-21.

[8] CAMMENGA Z A, BAKER C J, SMITH G E, et al. Micro-doppler target scattering [C] ∥Radar Conference, Cincinnati, OH: IEEE, 2014: 1451-1455.

[9] 肖立, 周剑雄, 何峻, 等. 弹道中段目标进动周期估计的改进自相关法 [J]. 航空学报, 2010, 31(4): 812-818.

[10] 邵惠民. 数学物理方法 [M]. 2版. 北京: 科学出版社, 2010: 357-358.

[11] 周旭广, 苏涛, 黄科, 等. 基于CLEAN算法的HFM脉压信号研究 [J]. 舰船电子对抗, 2014, 37(2): 74-78.

[12] HEUNGSUN Park, STEFANSKI L A. Relative-error prediction [J]. Statistics and Probability Letters, 1998, 40(3): 227-236.

Group-target Signal Separation and Reconstruction Based on Matched Space Transform

WANG Yizhe,FENG Cunqian,LI Jingqing

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

In view of the problem of intricate overlap and difficult separation in midcourse group-target echo by narrowband radar, a novel algorithm based on matched space transform was proposed to extract its micro-Doppler features. On the basis of modeling of group-target, period of each sub-target was obtained using autocorrelation method first. Then with the characteristic of micro-Doppler curve along time variable, the corresponding matched space was structured. Finally, the parameters of each scattering point were estimated utilizing energy peak searching and CLEAN algorithm. Thus the echo was reconstructed. Simulation results indicate that the proposed method can achieve favorable identification despite of background noise and signal aliasing.

group-target; micro-Doppler; matched space transform; time-frequency analysis

2015-06-03

国家自然科学基金(61372166);陕西省自然科学基础研究计划(2014JM8308)资助

王义哲(1992-),男,河南驻马店人,硕士研究生,研究方向:雷达信号处理及电子战研究。

TN957

A