固冲发动机推力测量系统动态建模与分析*
谢海刚,李 纲
(中国空空导弹研究院,河南洛阳 471009)
固冲发动机推力测量系统动态建模与分析*
谢海刚,李 纲
(中国空空导弹研究院,河南洛阳 471009)
针对固冲发动机地面试验中点火过程推力测量信号失真的问题,对推力测量系统进行了动态建模。采用ARMAX模型为基础的试验建模方法,设计实施了辨识试验,得到了不同激励下的响应信号。依据试验结果辨识出了模型的结构与阶次,建立了推力测量系统的动态模型。通过分析模型适配率和评估残差白色性,验证了模型准确有效。时域和频域分析结果表明,该动态模型可真实反映推力测量系统的动态特性,为改善动态特性、增加推力补偿和恢复真实信号奠定了基础。
固冲发动机;推力测量;动态建模
0 引言
在固冲发动机地面连管试验中,推力随时间的变化规律是发动机性能评定的重要依据之一。固冲发动机点火初始段是非定常动态过程,推力变化快速且复杂,常用推力测量系统一般用于稳态推力测量,固有频率较低,测量点火初始段的动态过程推力时,信号会振荡失真,并非准确的真实值。
通过建立固冲发动机推力测量系统的动态模型,分析其动态特性,修正或复现点火过程的真实推力,是解决信号振荡、提高推力测量准确度的关键。在固体火箭发动机试验领域,国内外已进行过动态力的理论研究及实践工作[1-3];但在综合了进气模拟、排气反压及柔性台架等因素的固冲发动机试验领域,尚未见工程实践报道。
固冲发动机推力测量系统采用柔性推力台架,结构复杂,影响因素多,理论建模困难。文中基于系统辨识理论,设计辨识试验,获得系统输入输出数据,并依据实测试验数据提取模型信息,采用预测误差辨识方法构建系统黑箱模型,并对模型进行验证与特性分析。
1 固冲发动机推力测量系统
固冲发动机推力测量系统一般由柔性推力台架(含动架、定架和柔性板簧)、稳流舱、波纹管、整流段、静态校准装置、试验产品和推力传感器组成,如图1所示。
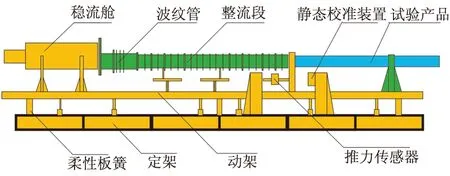
图1 固冲发动机推力测量系统
该台架上的力是综合进气阻力、稳流舱滚动摩擦阻力、整流段支撑滑动阻力、高空舱摩擦阻力和产品真实推力的复合值,采用柔性结构,可以有效消除阻力对测量的不利影响,但同时也造成了推力测量系统的整体固有频率较低。
试验产品的典型工作段分为起始段、稳定段和结束段,其中,稳定段推力随时间变化不大,经原位静态校准后,测量精度可优于0.5%,台架低固有频率对其影响不大;但在起始段和结束段,快速变化的推力为动态力,当其频率超过某一值时,测量结果就出现振荡现象,与真实值严重偏离,如图2、图3所示。
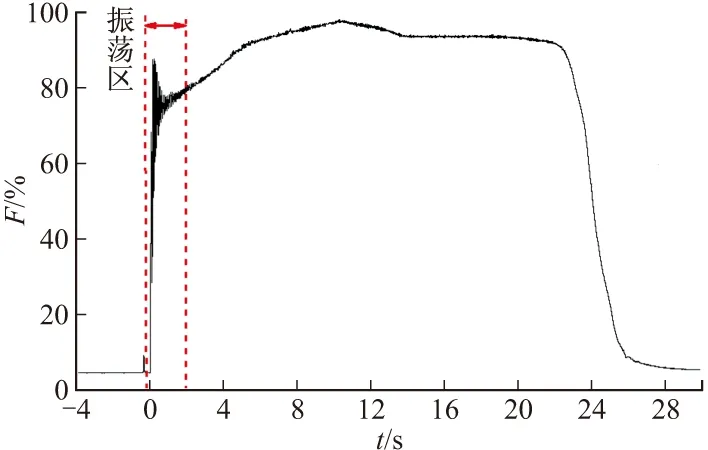
图2 推力振荡曲线
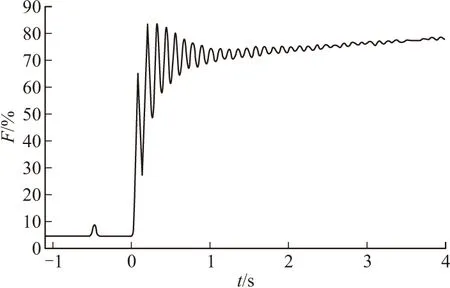
图3 振荡区放大曲线
这种情况下的动架位移和推力传感器输出并不能代表试验产品的真实推力,系统输入与输出已为非线性关系。这就说明,推力测量系统动态性能的好坏直接影响着测量结果的准确度。
对推力测量系统进行动态建模,获得系统的真实模型,并对模型加以特性分析,可以针对性的改善推力测量系统的动态特性,为恢复和复现真实有效的推力数据奠定基础[4]。
2 动态建模辨识原理
固冲发动机推力测量系统建模方法可分为理论建模和试验建模。复杂的系统结构,导致理论建模过于复杂;而推力测量系统的动态特性必然存在于测量过程中的输入输出数据之中,只要设计合理的试验,就可通过试验建模法获得输入输出数据,从而提取信息建立动态模型。
试验建模过程为:首先根据辨识的先验知识设计辨识试验,获得实际输入、输出数据;依据一定的准则,估计结构参数和模型参数;得出模型后,必须对其进行检验获得最优模型。
其中,关键问题是结构辨识和参数辨识。结构辨识是选择模型类和确定模型阶次。推力测量系统选择的模型类为ARMAX模型(自回归滑动平均模型),不仅可描述系统的输入输出关系,而且可描述有色测量噪声,其主要结构如图4所示。

图4 ARMAX模型结构
ARMAX模型的一般形式:
(1)
式中:u(k)、z(k)分别为系统输入、输出序列,e(k)为均值为零的不相关随机噪声序列。A(z-1)、B(z-1)和C(z-1)为阶次分别为na、nb和nc的多项式。
阶次辨识采用最终预报误差(FPE定阶法)进行确定。将估计模型的阶次从小开始逐渐增加,分别求得最终预报误差(FPE),找出FPE最小的阶次,该阶次为模型阶次的估计值。
ARMAX模型的FPE(na,nb,nc)为:
(2)
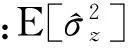
3 辨识试验
试验通过选择一定的激励信号,为推力测量系统提供激励,测得系统在该激励下的响应。
3.1 激励信号
合适的激励信号是辨识试验最重要的环节。要求为:a)激励源的频谱可覆盖推力测量系统的全部模态频率;b)激励力的量级与推力测量系统实际推力估算值接近[5]。动态力测试常用理想阶跃信号、斜坡阶跃信号作为输入,其在二阶系统下的特性分别如图5、图6所示。
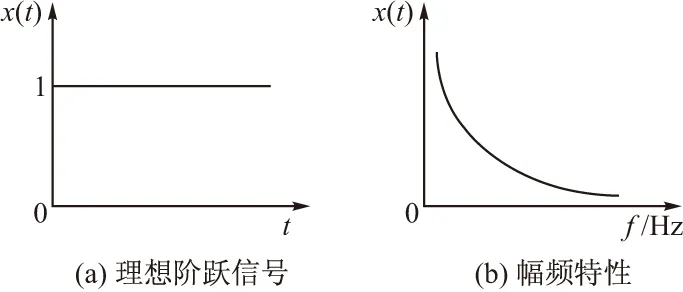
图5 输入为理想阶跃信号的幅频特性
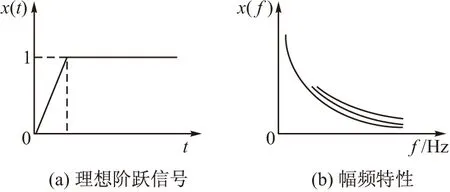
图6 输入为带斜坡的阶跃信号的幅频特性
激励信号可通过砝码加载法实现。通过加载标准砝码对推力测量系统测力轴心方向施加一个标准静态力,由快速释放机构对该力值进行快速卸载,这样,就可获得一个近似理想的阶跃力,达到了辨识试验力源的要求。
3.2 试验设计
砝码加载法是获得负阶跃力的有效方法。辨识试验设备组成有:负阶跃力加载装置、推力测量系统和数据采集系统,如图7所示。
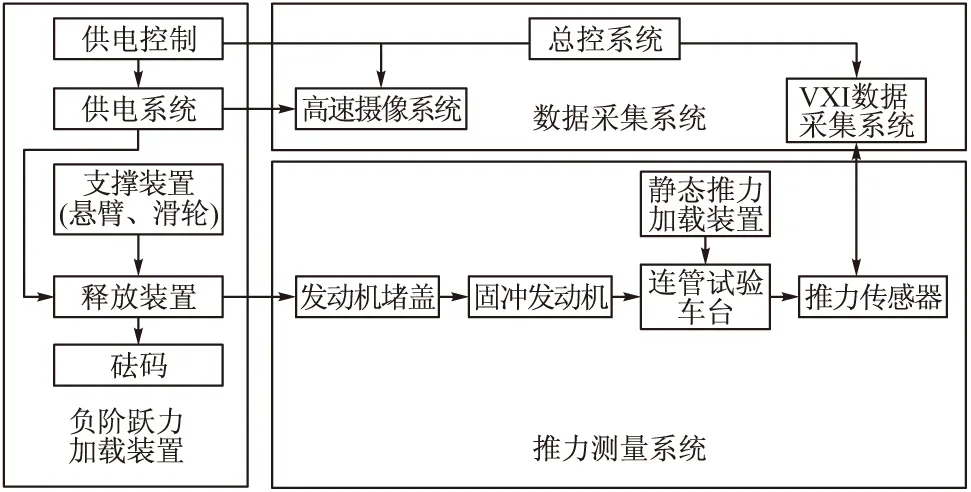
图7 辨识试验设备组成图
1)负阶跃力加载装置:含控制模块、支撑装置、快速释放结构和标准砝码等,实物图如图8所示,主要实现力值的加载与快速释放。

图8 负阶跃力加载装置
2)数据采集系统:含总控系统、VXI数据采集系统和高速摄像系统。
3)推力测量系统包含试验车台(含动架和定架)、固冲发动机、尾部堵盖、推力传感器和静态推力加载装置等;主要实现试验产品的固定、标准力值的加载和响应信号的输出。
系统辨识试验原理为:经静态推力加载装置进行原位标定后,向负阶跃力加载装置加载一定质量的砝码,在产品轴心方向产生一个拉力,通过总控系统发出多路启动信号,同步运行所有设备,快速释放机构瞬间卸载砝码,产生一个负的阶跃力作用,响应信号通过数据采集系统获得。
试验采用3种载荷:20 kg、50 kg和100 kg,各加载3次,试验流程如图9所示。
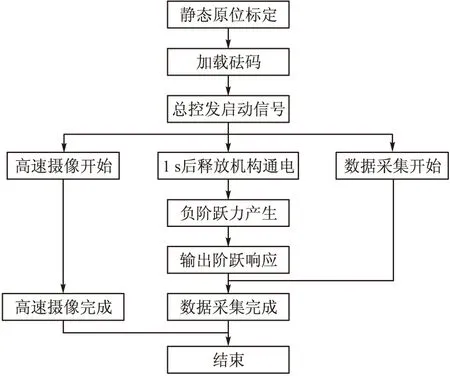
图9 系统辨识试验流程
3.3 系统辨识试验结果
各载荷下的阶跃响应曲线如图10、图11和图12所示。
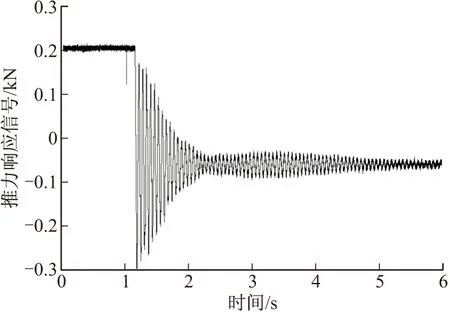
图10 阶跃响应曲线(载荷20 kg)
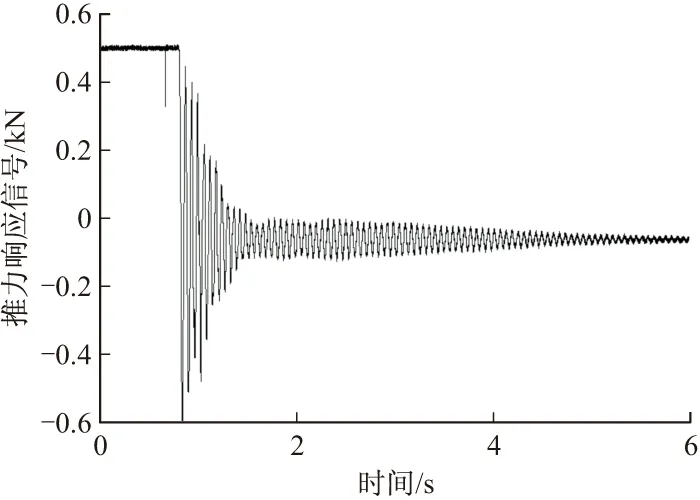
图11 阶跃响应曲线(载荷50 kg)
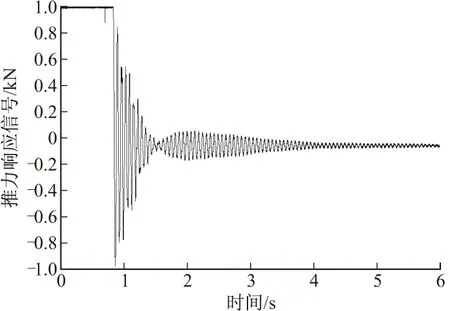
图12 阶跃响应曲线(载荷100 kg)
响应信号和启动信号同步性对比结果见图13,可知两个信号工作起点同步。该结果说明启动信号发出瞬间,快速释放机构就卸载了砝码,动作时间与高速摄像对比一致,因此,该时间满足近似理想阶跃信号输入的要求。
激励信号幅值与响应信号的稳态值一致,下降时间很短,可构造获得。如20 kg载荷时的激励信号如图14所示。
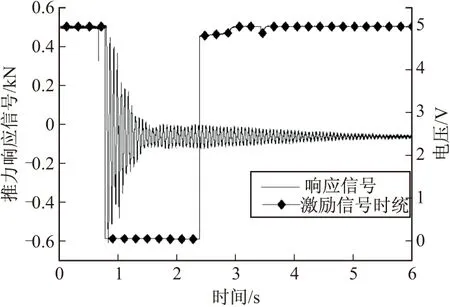
图13 响应信号与启动信号同步性
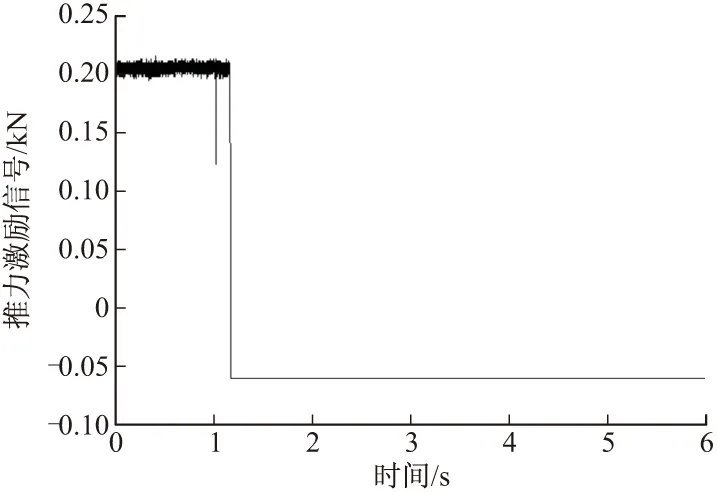
图14 激励信号(20 kg)
4 模型辨识
4.1 数据预处理
为提高辨识精度,选取1.109 6 s~2.319 2 s的测试数据。同时对原始数据进行滤波、剔除高频成分、消除趋势项和重新采样[6],一部分用于模型辨识,另一部分用于数据验证。
通过Matlab系统辨识工具箱中的dtrend函数、idfilt函数、idresamp函数进行重采样以插值、删减数据。
预处理后的数据曲线如图15所示。
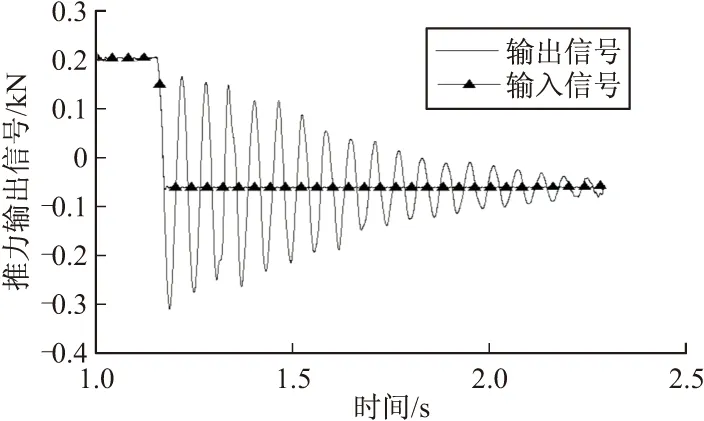
图15 预处理后的输入输出数据曲线
4.2 结构及参数辨识
结构辨识采用ARMAX模型,结构为:
A(z-1)z(k)=B(z-1)u(k)+C(z-1)e(k)
(3)
利用FPE准则对模型不同的na、nb阶次下的估计结果如表1所示。
从表1可以看出,较小的FPE值出现在na=3、nb=2时,因此模型较适合的阶次为:na=3、nb=2。
确定了模型类和阶次,参数辨识结果如下:
(4)
模型的损失函数为1.170 43e-005,FPE为1.173 14e-005。
将差分方程转化,可获得推力测量系统的离散传递函数模型为:
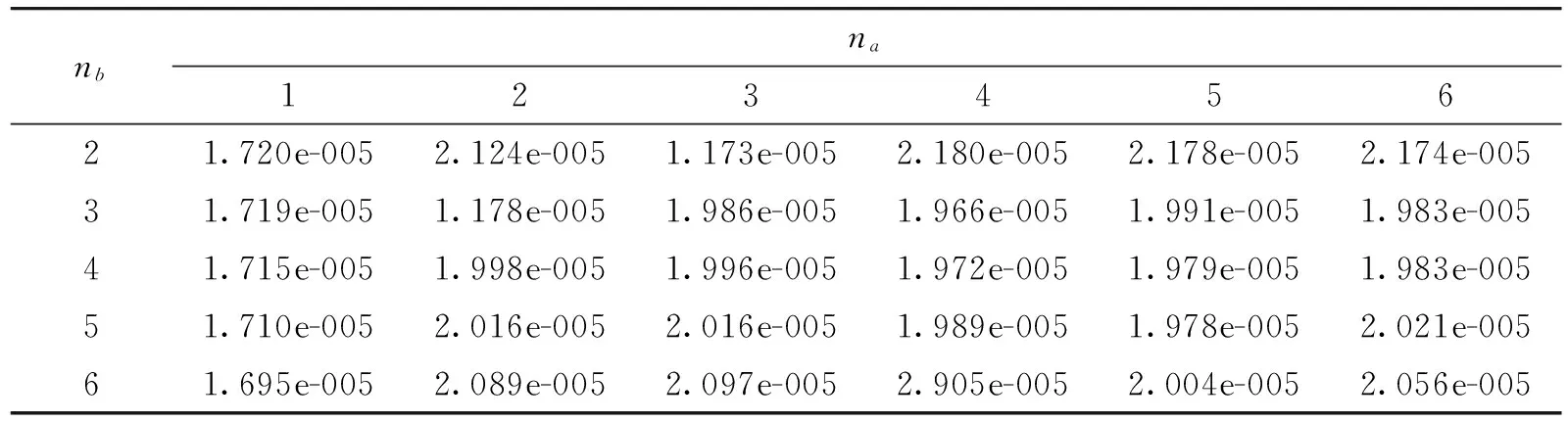
表1 不同na和nb阶次下所对应的FPE值
(5)
4.3 模型检验
获得na=3的模型后,进行变换阶次获得了na=2、na=4的模型,分别将其模型仿真输出与测量实际输出进行比较,结果如图16所示。
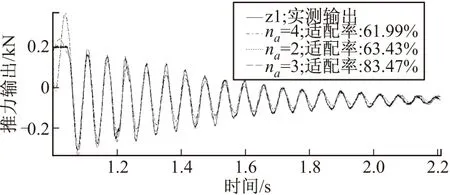
图16 不同阶次下的系统实测输出与模型仿真输出比较
从图中模型适配率可知,na=2为63.43%,na=4为61.99%,na=3、nb=2的模型输出与测量实际输出的吻合最好,适配率达到83.47%。
模型残差的白色性可通过计算模型残差序列{ε(k)}的自相关函数Rε(τ)判定,若Rε(τ)在一个接近于0的区间(置信度为α,τ≠0)内波动,则可认为{ε(k)}为白噪声。模型残差如图17所示,可见Rε(τ)大部分是在置信区间之内,因此,模型残差可认为是置信度较好的白噪声。
由以上检验结果可知,系统辨识所得模型可信。
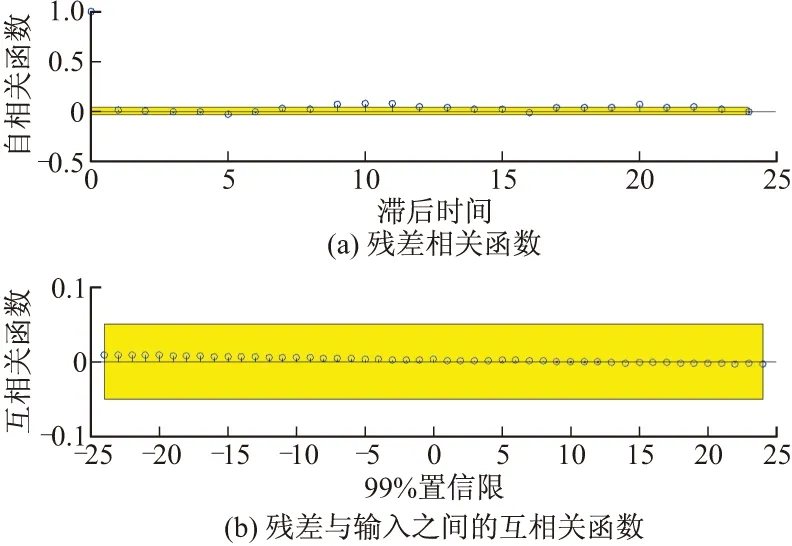
图17 模型残差
5 动态特性分析
依据所建模型,以理想阶跃信号为输入,仿真可得阶跃响应曲线[7],如图18所示。
由阶跃响应曲线可得时域特性,推力测量系统的动态模型虽为三阶,但影响其动态性能的主要环节表现为二阶系统,系统中的二阶环节起到了主导作用,其余环节可认为放大环节。
对差分方程形式的动态模型进行Z变换,可得离散传递函数,再经双线性变换可得系统连续传递函数为:
(6)
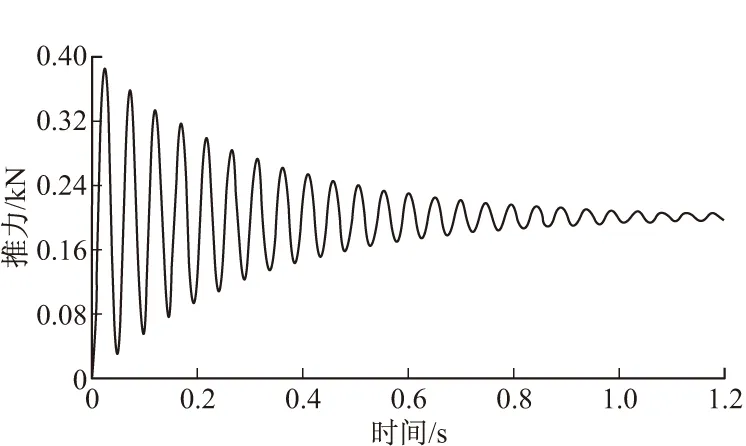
图18 推力测量系统动态模型的阶跃响应
仿真得出该动态模型的幅频、相频特性曲线如图19、图20所示。从该图可以看出,幅频曲线平直段不是很长,推力测量系统的固有频率不高,在频率低时,相位差与频率基本保持线性关系,频率较高时,相位差与频率已是非线性关系。
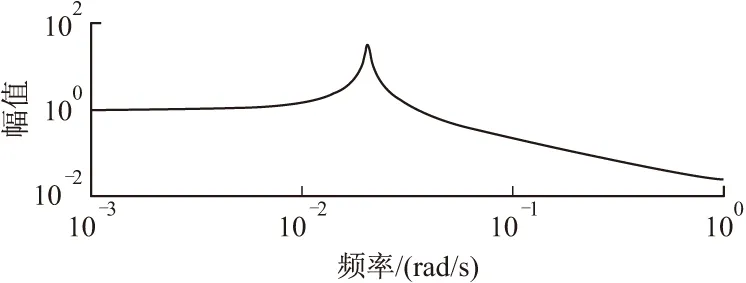
图19 模型幅频动态特性曲线
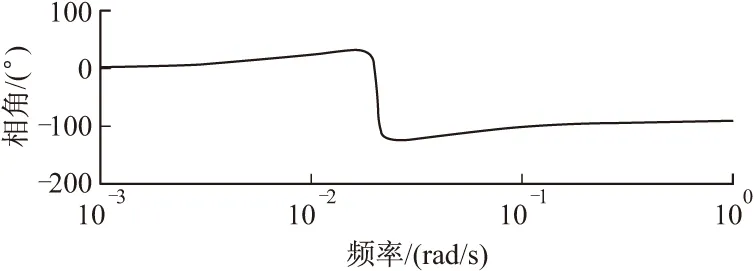
图20 模型相频动态特性曲线
6 结论
通过辨识试验获得了固冲发动机推力测量系统的动态模型,模型仿真输出和实测数据对比结果表明,ARMAX模型类和阶次的选择、辨识试验的设计合理有效,模型参数估计准确;对模型进行时域和频域特性分析结果表明,推力测量系统的动态特性主要受二阶环节影响,固有频率对系统动态特性影响较大,较高频率时系统已无法保证线性输出。该动态模型的建立为进一步的改善推力测量系统的动态特性、增加推力补偿环节和恢复真实被测信号奠定了基础。
[1] DEAN D S, 张峻城. 火箭发动机推力瞬变的测量 [J]. 固体火箭技术, 1982(2): 106-115.
[2] 欧阳华兵. 固体火箭发动机瞬态推力测量 [D]. 杭州: 浙江工业大学, 2005: 11-14.
[3] SASOH Akihiro,ARAKAWA Yoshihira. A high-resolution thrust stand for ground tests of low-thrust space propulsion devices [J]. Rev. Sci. Instrum, 1993, 64(3): 719-723.
[4] 李俊华, 张平. 动态推力频域恢复技术 [J]. 固体火箭技术, 1996, 19(1): 69-74.
[5] 赵自文. 动态推力校准系统设计 [J]. 自动化仪表, 2007, 28(增利): 228-230.
[6] 侯媛彬, 汪海, 王立琦, 等. 系统辨识及其Matlab仿真 [M]. 北京: 科学出版社, 2004: 81-88.
[7] LJUNG Lennart. System Identification Toolbox: User’s Guide[M]. MathWorksInv, 1995: 17-24.
Dynamically Modeling and Analysis of Thrust Measurement System for Solid Ramjet
XIE Haigang,LI Gang
(China Airborne Missile Academy, Henan Luoyang 471009, China)
For ignition thrust measurement distortion of solid ramjet in ground test, a dynamic model for thrust measurement system was built. The responses at different excitation signals were obtained by designing and implementing identification test which based on ARMAX model. According to the test results, structure and order were identified and the dynamic model for thrust measurement system was built. Veracity and effectiveness of model were verified by fitting rate analysis and residual whiteness estimation. Time-frequency domain analysis results show that the dynamic model could be used to reflect actual dynamic characteristics of thrust measurement system, laying a foundation for improvement of dynamic characteristics, adding thrust compensation and real signals resume.
solid ramjet; thrust measurement; dynamically modeling
2015-11-08
空装预研课题资助
谢海刚(1984-),男,河南洛阳人,工程师,硕士,研究方向:动态参数测量技术。
TJ760.6
A

