重视课本习题，举一反三

薛朝晖

重视课本习题，举一反三

薛朝晖

苏科版七（下）第七章30页习题7.5第4题：

如图1，已知AB∥CD，BE平分∠ABC，CE平分∠BCD.射线BE与CE交于点E.求证：BE⊥CE.

又由AB∥CD，知∠ABC+∠BCD=180°，

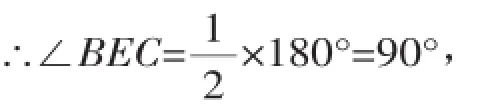
即BE⊥CE.

【分析一】由角平分线的定义，易得∠1、∠2与∠BCD、∠ABC之间的倍分关系，再利用“两直线平行，同旁内角互补”的结论进行整体代换，即可解决问题.

解法1（整体转化法）

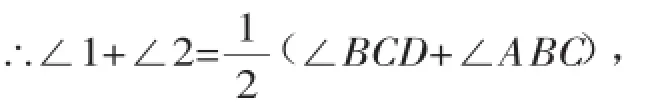
又AB∥CD，∴∠BCD+∠ABC=180°，

∴∠E=180°-（∠1+∠2）=180°-90°= 90°，即BE⊥CE.

【分析二】作平行线，把∠E分成两个角，并将这两个角与∠1、∠2联系起来，进行有效转化.

解法2（分解转化法）

解：如图2，过点E作EF∥AB，交BC于F，

又AB∥CD，∴AB∥EF∥CD.

【分析三】要求∠E，只需求出∠E的邻补角，延长BE后，出现新的△CEM（如图3），△CEM的三个内角分别与△BEC的三个内角相等，用对应思想便可解决问题.

解法3（对应转换法）

解：延长BE交CD于点M.

∵AB∥CD，∴∠CME=∠ABE=∠2，

又∠1+∠2+∠BEC=∠ECM+∠CME+∠CEM=180，

而∠1=∠ECM，∠2=∠CME，

∴∠BEC=∠CEM.

又∠BEC+∠CEM=180°，

即BE⊥CE.

【总结】把此习题概括成一句话就是：两条平行线被第三条直线所截，一对同旁内角的角平分线互相垂直.

通过对此习题的多种解法的深入探讨，可以加强知识间的联系，实现方法和技能的融会贯通，从而培养思维的深刻性和灵活性.

【变式一】探求原习题的逆命题

例1参照图1，两条直线AB、CD被第三条直线BC所截，所成的同旁内角的平分线BE和CE互相垂直，探求AB与CD的位置关系.

解：∵BE⊥CE，∴∠1+∠2=90°.

又BE、CE平分∠ABC、∠BCD，

∴∠ABC+∠BCD=180°，

∴AB∥CD.

【说明】进一步可把原习题的条件与结论进行梳理，总结如下：在图1中，直线AB、CD被BC所截，①AB∥CD，②BE平分∠ABC，③CE平分∠BCD，④BE⊥CE，以上任三个作为条件都可以推出第四个.

【变式二】在原图基础上，增加另一组同旁内角平分线

例2如图4，已知AB∥CD，BE、CE、BF、CF分别是∠ABC、∠BCD、∠MBC、∠NCB的角平分线，BC不与ND垂直，则图中与∠FBE相等的角共有多少个？

解：由原题可知∠E=90°，同理可得∠F=90°.

图4

同理可得∠FCE=90°.

∴∠FBE=∠E=∠F=∠FCE=90°，

即与∠FBE相等的角共有3个.

【说明】本题可表述为：两条平行线被第三条直线所截，两对同旁内角的平分线组成的四边形是矩形.

【变式三】在原图基础上，增加两个相等的角或一组平行线

例3如图5，∠GEF与∠DFE的平分线交于点H，AB∥CD，∠B=∠D，求证：EH⊥HF.

图5

证明：∵AB∥CD，∴∠A=∠C，

由已知∠B=∠D，∴∠AEB=∠DFC，

又∠AEB=∠GEF，∠DFC=∠MFE，

∴∠GEF=∠MFE，∴EG∥FD，

则∠GEF+∠EFD=180°，

又EH、FH为角平分线，

即EH⊥HF.

【说明】在原习题的基础上添加平行线后，得到一对内错角相等，并结合其他条件进一步得出BG∥MD，这样就将看似复杂的问题逐步转化成已经解决过的问题（即原习题）.

由上可见，试题一般都是从经典习题变化而来的，在平时的学习中，我们应该高度重视一些典型例题和它们的解法，充分挖掘其蕴含的数学本质，实现知识和技能的融会贯通，从而提高解题能力，做到举一反三.

（作者单位：江苏省丹阳市华南实验学校）