一道课本例题的多角度探索

吴建良

一道课本例题的多角度探索

吴建良

课本中的例题一般都具有基础性、典型性和延伸性等特点.在学习过程中，同学们要注重对例题的研究与探索，下面以苏科版教科书七年级上册第156页例题为例进行说明.

例题如图1，∠AOD=80°，OB是∠AOC的平分线，∠AOB=30°.求∠AOC、∠COD的度数.

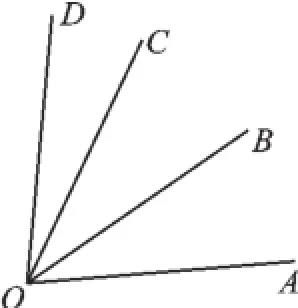
图1

解：∵OB是∠AOC的平分线，

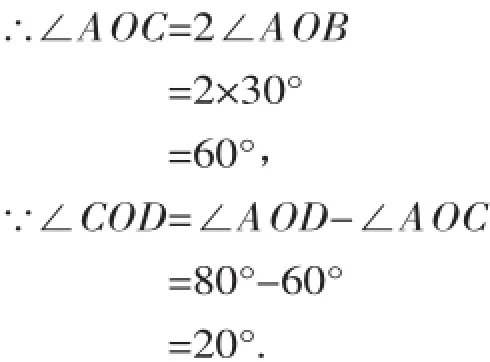
变式一如图2，∠AOD=80°，OE是∠AOD的平分线，∠AOC=60°.求∠COE的度数.

图2

解：∵OE是∠AOD的平分线，

变式二若已知∠AOD=80°，OE是∠AOD的平分线，OC是过O的一条射线，∠AOC=60°.求∠COE的度数.

【简析】由于OC是过O的一条射线，OC可以是∠AOD内部的一条射线，也可以是∠AOD外部的一条射线，所以要分两种情况解决.

解：（1）当OC是∠AOD内部的一条射线时，即为变式一的情形.

（2）当OC是∠AOD外部的一条射线时，如图3.

图3

∵OE是∠AOD的平分线，

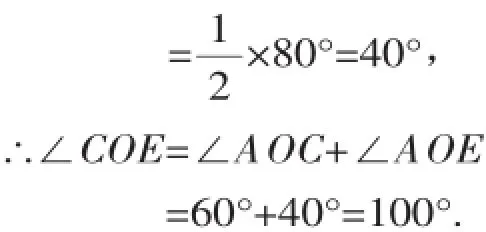
变式三如图4，∠AOD=80°，OB是∠AOC的平分线，OE是∠COD的平分线，求∠BOE的度数.

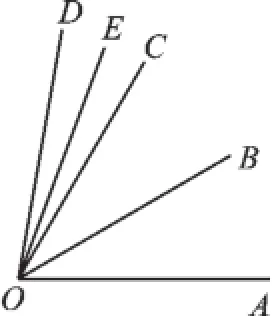
图4

解法1：

∵OB是∠AOC的平分线，

∵OE是∠DOC的平分线，

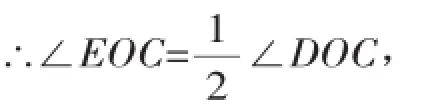
解法2：

∵OB是∠AOC的平分线，

∴∠AOC=2∠BOC，

∵OE是∠DOC的平分线，

∴∠DOC=2∠EOC，

∵∠AOC+∠DOC=∠AOD，

∴2∠BOC+2∠EOC=80°，

∴∠BOE=∠BOC+∠EOC=40°.

说明：在解法2中，由2∠BOC+2∠EOC= 80°到∠BOC+∠EOC=40°是关键的一步，它运用了等式的性质.

变式四：如图5，已知线段AB=m，点C为线段AB上一点，点D是线段AC的中点，点E是线段BC的中点，求线段DE的长.

图5

解：∵点D是线段AC的中点，

点E是线段BC的中点，

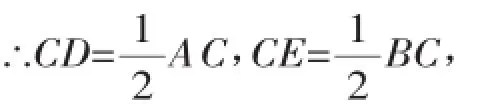
课本中许多例题和习题都值得这样探索，同学们如果能长期坚持一题多解、一题多变的探索，不仅有利于培养创新意识，而且还能提高探索能力.

（作者单位：江苏省吴江区实验初级中学）