基于不同假设的修正内含报酬率计算问题探讨*

袁太芳

(赣南师范大学 商学院，江西 赣州 341000)



·经济学研究·

基于不同假设的修正内含报酬率计算问题探讨*

袁太芳

(赣南师范大学 商学院，江西 赣州 341000)

在给出MIRR定义、特征的基础上，指出其存在的不足，分析了MIRR在基于“收支两条线”“收支相抵”和“资金垫支最少”假设下的计算，并总结了不同假设下的规律，明确在NPV>0的情况下，“资金垫支最少”假设计算的MIRR最符合实际，和投资者的“用最少的资金获得最大的收益”的目标也最相符；在NPV<0的情况下，可以充分利用成本低于i或无息的债务资金作为杠杆，相应地提高自有资金的MIRR，也使自有资金的NPV>0。

项目投资；现金净流量；净现值；内含报酬率；修正内含报酬率

企业在进行投资决策时通常采用体现了货币时间价值的净现值(NPV)和内含报酬率(IRR)这两个主要指标。一般情况下，净现值与内含报酬率指标能得出一致的决策结论，但是在对互斥方案和非常规方案项目的决策中有时会出现矛盾。在出现矛盾时，大多认为使用净现值是正确的选择，原因在于净现值反映了企业的财务目标，但净现值的缺点是不能真实反映项目的实际报酬率。

对内含报酬率，不仅有计算过程复杂、可能出现多个解等不足，而且在利用内含报酬率进行投资决策时，对于NPV可行的项目，会过分高估收益；而在NPV不可行的项目中，又会过分低估收益。[1]特别是在非常规项目中，内含报酬率会出现多个或没有的情况，这时可能导致决策错误。NPV和企业的财务目标一致，使用其作为投资项目决策指标可以得出正确的决策，但是NPV不能反映实际的投资报酬率，为了知道实际的报酬率并且能做出正确的投资决策，由此提出修正的内含报酬率，即MIRR。

一、MIRR现行计算模型及存在的问题

(一)现行计算模型

对于修正的内含报酬率也有不同的修正方法，主要有两种观点：

第一种观点：以基准折现率为折现率，将所有的净现金流出折成现值(初始投入)，将所有的净现金流入折成终值(最终收益值)，使最终收益值折现后与初始投入值相等时的折现率，即为修正内含报酬率。[2]

第二种观点：非常规项目中发生的现金流出是企业为取得投资收益而付出的成本代价，所以应该按资金成本率折现。[3]

不论哪种观点，其特征都是以投资必要报酬率作为现金流入的再投资率。但第一种观点更符合实际，不会过分高估项目的内含报酬率。

本文主要以第一种观点来说明MIRR，在这种情况下，不论是独立投资项目、互斥项目还是非常规项目，都折成期初和期末两部分来计算，这样就可以避免NPV与IRR的矛盾，也不会出现IRR多个或没有的情况。

一般来说，内含报酬率要比修正内含报酬率(MIRR)大，而更小的MIRR，会使项目评估更接近实际。[4]

计算公式[5]为(略有变形，但本质不变)：

[CIF0(1+k)n-0+CIF1(1+k)n-1+…+ CIFn(1+k)n-n](1+MIRR)-n+[COF0(1+k)-0+COF1(1+k)-1+…+ COFn(1+k)-n]=0

COF为现金流出，CIF为现金流入，K为资本成本率，n为投资受益期。此处为计算的一致性，定义COF小于0,CIF大于0。

在应用MIRR进行投资决策时，关键是如何区分现金流出、现金流入。一般情况下，假设：(1)项目建设期主要为现金流出，均在建设期的每期期初发生；(2)垫支流动资金在项目生产经营期的期初投入(视同现金流出)，期末收回(视同现金流入)；(3)经营期的营业现金流量发生于每期期末；(4)终结现金流量在项目的终结时点发生，一般为现金流入。

(二)存在的问题

通过MIRR定义的计算方程可知，MIRR可以利用开n次方求出，计算过程更加简单，也不可能出现多解(要求MIRR>0)的情况。

虽然经营期的营业现金流量假设发生于每期期末，但经营期的营业现金流量有经营现金流入量、经营现金流出量计算而得，这就不得不提出一个问题：对于经营期的经营现金流量，从计算经营现金净流量的各组成项的视角，是按本期的现金净流量(NCF)的正负号来确定列入初始投入(NCF<0)或最终收益值(NCF>0)，还是先将本期的现金净流量(NCF=CIF+COF，一般情况下，COF<0，下同)分成两部分经营现金流入量、经营现金流出量，再将经营现金流出量列入初始投入，经营现金流入量列入最终收益值？在现行的计算模型中没有予于确定。

事实上，采用何种观点，主要是基于不同的假设，一种是“收支两条线”假设，另一种是“收支相抵”假设。基于投资者的视角，投资者总是希望垫支尽可能少的资金，因而产生“资金垫支最少”假设。无论何种假设，现金净流量分成经营现金流入量、经营现金流出量的结果都应该是唯一的。

为更好地分析，引入NPV>0、NPV<0两种情况下的案例。

引例1(NPV>0情况)：假设必要报酬率为10%，其他资料如表1所示。

表1 项目的现金净流量 单位：万元

该项目为非常规项目，IRR可能不适用，经过计算，其净现值为NPV=1 442.4万元，NPV>0。

引例2(NPV<0情况)：假设必要报酬率为10%，其他资料如表2所示。

表2 项目的现金净流量 单位：万元

该项目也为非常规项目，IRR可能不适用，经过计算，其净现值为NPV=-203.7万元，NPV<0。

那么，针对上述案例，基于“收支两条线”假设、“收支相抵”假设和“资金垫支最少”假设下，MIRR如何计算？其计算结果有何规律，产生此规律的原因，可以得出何结论？

二、“收支两条线”假设下的MIRR计算

“收支两条线”假设是指在经营期末的现金结算不得现金坐支，收支分离，现金收入、现金支出按两条线分别结算，即在现金净流量NCFi=CIFi+COFi计算中，只考虑CIF、COF，不考虑NCF。CIF主要指现金销售收入、其他现金收入和终结现金流入等，COF主要指初始现金流出、经营现金支出、相关项目的企业所得税等。“收支两条线”假设的核心是当期的现金流入既不得用于当期的现金支出，也不得用于后续各期的现金支出，只能由投资者从外部投入，各期的现金流入也只能由投资者收回。此假设适用于现金收入必须上交集团总部，现金支出必须通过总部审批的财务集中核算项目。

收支两条线的情况，即NCFi=CIFi+COFi不变，但COFi*CIFi≤0(i=0,1,…,n)。COF、CIF的确定方法是：先确定CIF，为各期收付实现制下确定的预计收入；再根据现金流量计算方法确定的NCF，利用NCF=CIF+COF推算出COF。

在“收支两条线”假设下，要求企业对项目垫支资金为：各期COF的绝对值之和。

如引例1，在“收支两条线”假设下，要求企业对项目垫支资金为：

1 920+600+4 000+500+1 250+1 000=9 270万元。

表1中给出了“收支两条线”假设下COF、CIF的数据，根据MIRR的定义，可得MIRR的计算方程(项目要求的必要报酬率为10%)：

[3 000(1+10%)4+950(1+10%)3+1 500(1+10%)2+3 750(1+10%)1+3 000](1+MIRR)-5-[1 920+600(1+10%)-1+4 000(1+10%)-2+500(1+10%)-3+1250(1+10%)-4+1 000(1+10%)-5]=0

利用内插值法，可求得MIRR=13.88%。

如引例2，在“收支两条线”假设下，要求企业对项目垫支资金为：

1 920+600+4 000+500+800+1 000=8 820万元。

表2中给出了“收支两条线”假设下COF、CIF的数据，根据MIRR的定义，可得MIRR的计算方程(项目要求的必要报酬率为10%)：

[3 000(1+10%)4+950(1+10%)3+1 500(1+10%)2+1 800(1+10%)1+2 000](1+MIRR)-5-[1 920+600(1+10%)-1+4 000(1+10%)-2+500(1+10%)-3+800(1+10%)-4+1 000(1+10%)-5]=0

利用内插值法，可求得MIRR=9.38%。

三、“收支相抵”假设下的MIRR计算

“收支相抵”假设是指在经营期末的现金结算以现金收入减去现金支出的差额结算，即在现金净流量NCFi=CIFi+COFi(COFi<0)计算中，只考虑NCF，不考虑CIF、COF。若NCFi>0，则将NCFi视同CIFi；若NCFi<0，则将NCFi视同COFi。适用于现金收入不需上交集团总部的独立核算项目公司，此类项目公司一般是一个利润中心，而非投资中心。

收支相抵的情况，即经营期的营业现金净流量发生于每期期末，若其净流量为正数则等价于现金流入，若其净流量为负数则等价于现金流出；为简化起见，可以“同一项目中的当期(一般以年为期间)现金流入优先用于当期的现金流出，但不得用于后期支出”为假设，则推出各期现金净流量的基础上，正数为现金流入，负数为现金流出, COFi和CIFi至少有一个等于零，即COFi*CIFi=0(i=0,1,…,n)。

在“收支相抵”假设下，要求企业对项目垫支资金为：各期现金流量为负数的代数和的绝对值。不难看出，“收支相抵”假设下要求企业垫支资金小于“收支两条线”假设下要求企业垫支资金。 如引例1中，要求企业在项目中垫支的资金为1 920+3 050=4 970万元。

对案例的现金流量按“收支相抵”假设进行分析，可将其分成COF、CIF两部分，结果如表3所示。

表3 “收支相抵”假设的现金流量 单位：万元

由于项目要求的必要报酬率为10%，则按MIRR的计算定义，可列出计算方程：

[2 400(1+10%)4+1 000(1+10%)2+2 500(1+10%)1+

2 000](1+MIRR)-5-[1 920+3 050(1+10%)-2]=0

利用内插值法，可求得MIRR=16.38%。

如引例2中，要求企业在项目中垫支的资金为1 920+3 050=4 970万元。

对案例的现金流量按“收支相抵”假设进行分析，可将其分成COF、CIF两部分，结果如表4所示。

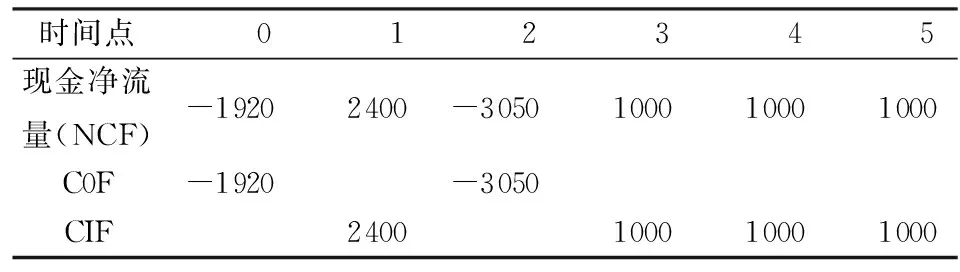
表4 “收支相抵”假设的现金流量 单位：万元

由于项目要求的必要报酬率为10%，则按MIRR的计算定义，可列出计算方程：

[2 400(1+10%)4+1 000(1+10%)2+1 000(1+10%)1+1 000](1+MIRR)-5-[1 920+3 050(1+10%)-2]=0

利用内插值法，可求得MIRR=8.98%。

四、“资金垫支最少”假设下的MIRR计算

“资金垫支最少”假设即“投资者总是希望垫支尽可能少的资金”假设，是指投资者对同一个投资项目，当期(一般以年为期间)现金流入在优先用于当期现金流出的基础上，若有剩余，则顺序用于下期或后续各期的现金净流出(此期的综合现金净流量计算出来为负数，就称为现金净流出)。注意，当期的现金流出优先使用当期的现金流入，不够才会动用前期剩余的资金。此方法适用于独立封闭运行的投资项目公司，此类项目公司一般是一个投资中心，因此和投资者的决策目标相一致。

在“资金垫支最少”假设下，要求企业对项目垫支资金的确定思路为：对顺序各综合现金流量，当NCFm<0(m=0,1,2,…)时，计算Σm=NCF0+NCF1+…+NCFm，所有的Σm(均小于0)计算出来后，取其中的最小值，此数的绝对值就是该项目需要垫支的最小资金量，也可称为项目累计最小投资额，此值对应的m可称为项目累计最短投资期。

按此思路，项目的各期综合现金流量分成唯一的现金流出、现金流入。方法为：在项目累计最短投资期内，在第一个NCFi>0(NCF符号由负变正)之前的NCF(现金流出期间)全部作为COF；项目累计最短投资期内的所有NCF>0的NCF均作为CIF；在项目累计最短投资期外的所有NCF均列入CIF。关键是对既在项目经营期间又在项目累计最短投资期的NCF<0必须分解成COF、CIF两部分，分解的原则是“现金流出优先用前属各期现金流入支付”， 累计的现金流出未达到前属现金流入期间的累计数之前均列入CIF，一旦超出，则超出部分列入COF。综合所有的分解结果，在不考虑时间价值的情况下，分解出的所有各期COF之和恰好等于项目累计最小投资额。

如表1，由于NCF0、NCF2小于0，则计算Σ0=-1 920万元，Σ2=-1 920+2 400-3 050=-2 570(万元)。最小值为-2 570万元，因此，项目累计最小投资额为2 570万元，项目累计最短投资期为2年。

对项目累计最短投资期为2年内的NCF0=-1 920万元列入COF，NCF1=2 400万元列入CIF，对项目累计最短投资期外的NCF3=1 000万元、NCF4=2 500万元、NCF5=2 000万元均列入CIF。关键是对NCF2=-3 050万元，先用NCF1=2 400万元支付，超出的650万元作为投资者的初始投入列入COF。计算结果见表5。通过表5，不难看出，COF之和为-1 920-650=-2 570万元，与项目累计最小投资额2 570万元相等。

表5 “资金垫支最少”假设 单位：万元

根据表5分析出的“资金垫支最少”假设下COF、CIF的结果，按照MIRR的定义，可得MIRR的计算方程(项目要求的必要报酬率为10%)： [2 400(1+10%)4-2 400(1+10%)3+1 000(1+10%)2+2 500(1+10%)1+2 000](1+MIRR)-5-[1 920+650(1+10%)-2]=0

利用内插值法，可求得MIRR=20.66%。

同理，可分析出引例2在“资金垫支最少”假设下COF、CIF的结果，如表6所示。

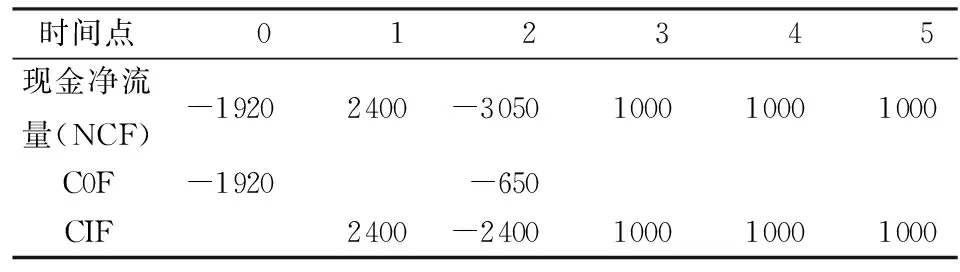
表6 “资金垫支最少”假设 单位：万元 单位：万元

项目累计最小投资额为1920+650=2570万元。按照MIRR的定义，可得MIRR的计算方程(项目要求的必要报酬率为10%)：

[2 400(1+10%)4-2 400(1+10%)3+1 000(1+10%)2+1 000(1+10%)1+1 000](1+MIRR)-5-[1 920+650(1+10%)-2]=0

利用内插值法，可求得MIRR=8.1%。

五、不同计算假设下的规律分析

对上述引例1(NPV>0)、引例2(NPV<0)就分别“收支两条线”“收支相抵”和“资金垫支最少”三种假设下的MIRR计算结果如表7所示：

表7 不同假设下的MIRR指标对比

通过上述的案例分析可以发现：

(一)对同一方案，无论基于哪一种假设，在不考虑时间价值的情况下，各期的现金流量总和都相同。如引例1均为2 930万元，引例2均为430万元。

(二)不同假设下，企业垫支的资金总额不同。就“收支两条线”“收支相抵”和“资金垫支最少”假设依次为9 270(或8 820)万元、4 970万元、2 570万元，从常规投资原则来看，“资金垫支最少”假设比较符合理性的投资规则。

(三)在NPV>0的情况下，“资金垫支最少”假设计算的MIRR最大，“收支两条线”假设计算的MIRR最小，均大于计算NPV时的贴现率，其和投资者的“用最少的资金获得最大的收益”的目标是一致的。如引例1中，基于“资金垫支最少”假设下计算的MIRR=20.66%，大于“收支相抵”假设下的16.38%，也大于“收支两条线”假设下的13.88%。

(四)在NPV<0的情况下，“收支两条线”假设计算的MIRR最大，“资金垫支最少”假设计算的MIRR最小，均小于计算NPV时的贴现率。如引例2中，基于“收支两条线”假设下计算的MIRR=9.38%，大于“收支相抵”假设下的8.98%，也大于“资金垫支最少”假设下的8.10%。

引例1、2计算的MIRR不相等，一方面与不同的假设有关，另一方面与计算NPV的贴现率(即投资必要报酬率，下同)也有关。

以上规律仅是基于一个特例所得的结论，对一般的情况是否成立呢？为说明此问题，不妨先立足于“资金垫支最少”假设，再推到“收支相抵”及“收支两条线”假设。下面通过一般的推导来证明上述规律的普遍性。

已知a,b,M,N均为常数，且a>0，b>0，M>N≥0，n为正整数，i为折现率，假设对应方程：

[a+N(1+i)n](1+x1)-n=b+N的解为x1，

[a+M(1+i)n](1+x2)-n=b+M的解为x2，

且有a (1+x0)-n=b的解x0>i，则有x1>x2。

证明：x1>x2等价于 (1+x1)n>(1+x2)n等价于 [a+N(1+i)n]/(b+N)>[a+M(1+i)n]/(b+M) 等价于 a(M-N)>b(M-N)(1+i)n

即：a/b>(1+i)n

即：(1+x0)n>(1+i)n

等价于x0>i

说明：此结论要在财务可行性的基础上才成立。

同理可证：上述命题中，在其他条件不变的情况下，若x0

基于等式：[a+M(1+i)n](1+x)-n=b+M，若M→+∞，则x→i。可见：

1.NPV>0。在x0>i，项目按资金成本i垫支的资金M越多，x越严格单调递减趋向于i；充分利用项目自身的成本较低的为i的资金，为项目的盈余收益做出最大的贡献，体现了财务的正杠杆作用。在引例1中，a=[2 400(1+10%)4-2 400(1+10%)3+1 000(1+10%)2+2 500(1+10%)1+2 000]，b=[1 920+650(1+10%)-2]， N=2 400(1+10%)-2，M=[600(1+10%)-1+3 350(1+10%)-2+500(1+10%)-3+1 250(1+10%)-4+1 000(1+10%)-5]。

2.NPV<0。在x0

3.若N<0，及等式[a+N(1+k)n](1+x)-n=b+N中的与N或N(1+k)n有关的折现率k小于a,b计算的折现率i,则可使x>x0。也就是说，企业可充分利用借入资金和自有资金的筹资组合，用成本低于i或无息的债务资金，使形成自有资金的a，b基本同步地小一些，从而提高自有资金的MIRR，相应地也使自有资金的NPV>0。

六、结论及其建议

基于上述分析，可得以下结论：

(一)在计算MIRR时，不同假设适用于不同的范围。

(二)同一投资方案，在同一贴现率情况下，不同假设的NPV均相等。

(三)在NPV>0的情况下，“资金垫支最少”假设计算的MIRR最符合实际，因其和投资者的“用最少的资金获得最大的收益”的目标是一致的。

(四)在NPV<0的情况下，可以利用不同假设的规律分析结论，充分利用成本低于i或无息的债务资金，在保持各年的现金流量之和相等或稍小一些的情况下，以便提高项目的MIRR，相应地也使自有资金的NPV>0。

[1] 孙树垒,徐斌,王海燕.内部收益率的修正及比较[J].统计与决策,2010,(1):64-66.

[2] 赵卫旭,陈国栋.项目投资评价指标IRR和MIRR比较[J].中国管理信息化,2008,(20):39-40.

[3] 吴清,陈威.财务评价指标IRR的重新诠释[J].财会通讯,2013,(32):6-8.

[4] 刘彩华,范光羽.投资项目财务评价方法的理论探究[J].中国管理信息化,2010,(2):42-44.

[5] 张大联,黄越.净现值法与修正内含报酬率法在投资中的应用[J].西安工业学院学报,2004,(3):302-306.

责任编辑：侯伟浩

Analysis of the MIRR Calculations under Different Assumptions

YUAN Taifang

(SchoolofBusiness,GannanNormalUniversity,Ganzhou341000,China)

Based on the definition and the feature of MIRR, this paper points out the insufficient parts of it, further more, it analysis the MIRR base calculation under three assumptions: the "revenue and expenditure separation line" assumption、the "break even" assumption and the "cash advanced" assumption. From this research, it is found that: when NPV>0, the "cash advanced" assumption achieves the same goal with the investors' willing, who want to maximize the income with the least outcome; when NPV<0, the interest free liability can be used as financial leverage to raise the MIRR of the own money, and to lead the NPV of the own money above zero.

2015-05-26

10.13698/j.cnki.cn36-1346/c.2016.05.016

袁太芳(1968-)，男，江西赣州人，赣南师范大学商学院教授，硕士生导师，研究方向：财务管理、会计。

http://www.cnki.net/kcms/detail/36.1037.C.20161008.0930.014.html

F23

A

1004-8332(2016)05-0085-05