一道典型数列极限问题的多种解法*

刘合财，陈治友

(贵阳学院 数学与信息科学学院，贵州 贵阳 550005)



一道典型数列极限问题的多种解法*

刘合财，陈治友

(贵阳学院 数学与信息科学学院，贵州 贵阳 550005)

分别用两边夹法、Euler常数法、定积分法、实验法等四种方法研究了一道典型的数列极限计算问题，并进一步提出了求解数列极限问题的一般策略。

数列极限；两边夹法；Euler常数法；定积分法

0 引言

极限问题是数学分析中函数研究的基本问题，极限的求法灵活多变，常利用极限的四则运算性质、初等函数的连续性、等价无穷小替换、两个重要极限、洛必达法则等求解[1]-[2]。极限问题的求解方法常常“因题而异”，文献[3]总结了求解极限问题的多种求法，文献[4]专门针对积分极限讨论了一些具体求法。函数列的积分中值点的渐近性问题就是数列极限问题，研究数列极限问题的解法及策略有助于函数的各种渐近性问题的求解。本文就一道典型的数列极限问题进行研究，分别用两边夹法、Euler常数法、定积分法、实验法求解，最后提出了求解数列极限问题的一般策略。

1 一道极限问题

在《数学分析》或《高等数学》的教材中常遇到这样一道极限问题：

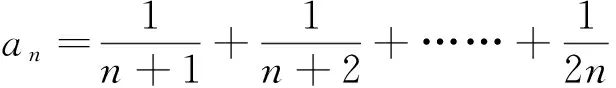
2 多种解法

这是一道典型的数列极限计算问题,其求解方法和思想十分重要。极限的思想贯穿高等数学课程的始终，一题多解，举一反三，对高等数学的教学和研究大有裨益。下面运用多种方法求解该极限问题。

两边夹法：利用不等式将该极限式作适当放大和缩小，使放大、缩小所得的数列的极限值相同，从而求得极限。难点在于利用不等式进行适当的放缩。

Euler常数法：利用已知极限及极限的运算性质,将原极限转化为已知极限的计算。难点在于找到与之紧密联系的已知极限。

解：已知极限

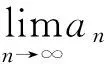
=γ-γ+ln2

=ln2

定积分法：将该极限化为特殊形式的和式的极限，构造出被积函数和积分区间，利用定积分求数列极限。难点在于积分区间和被积函数的构造。

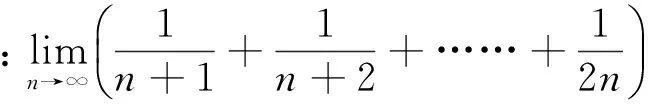
=ln2

由此可见，对和式进行适当的变形，构造被积函数及积分区间，利用定积分来计算数列极限是一条捷径。

实验法：使用Matlab、Mathematica等数学软件中的极限计算函数，求得极限值。如：Mathematica软件中，极限计算的函数形式为Limit[expr,n→∞]或Limit[expr,n→Infinity]。设置选项后还可以计算单侧极限。此外，还可以使用软件画出数列的散点图，观察数列的变化趋势，有助于极限计算。

解： 使用数学软件Mathematica 9.0 ，输入

运行后输出结果：Log[2]，从而求得该极限为ln2。

3 数列极限问题的解法策略

数列极限的求法有很多，但能做到“对症下药”才是关键。通常有以下基本策略可参考：

策略一：区分有限项数列的极限还是无限项数列的极限。有限项数列可考运用极限的四则运算性质、两个重要极限等方法计算数列极限，不能使用定积分法。无限项数列(特殊和式)的极限优先考虑定积分法，不能直接使用四则运算性质计算。

策略二：通过替换与变形化为已知极限或重要极限。替换与变形是非常重要的思想，引入新变量替换原有变量，转化极限的求解过程。变形则为转化为已知极限或重要极限提供方便。

策略三：实验法和两边夹法是“万能”解法。对于实验法，利用数学软件中的极限计算函数，按照规定的格式准确输入，就较快得到所求极限，无需计算技巧。对于两边夹法，只要熟练掌握不等式的性质以及放缩的技巧，总是可以把极限“套”出来。实验法和两边夹法普遍适用于有限项和无限项数列，可谓“万能”。

策略四：洛必达法则与函数的连续性是桥梁。由于洛必达法则是针对函数极限，若要求的是数列极限，不能直接运用洛必达法则，但可根据函数极限与数列极限的关系，算出相应的函数极限而求得。

4 结语

本文主要探讨了一道典型的数列极限的计算问题，分别运用了两边夹法、Euler常数法、定积分法和实验法求解，最后提出了求解数列极限问题的一般策略。对于数列极限问题，应充分利用极限式的表现特征，选择最适合的极限求法，才能达到事半功倍的效果。

[1]华东师范大学数学系.数学分析(第4版)[M].北京：高等教育出版社，2010.

[2]刘玉琏，傅沛仁，林玎，等.数学分析讲义(第4版)[M].北京：高等教育出版社，2003.

[3]裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社，1993：9-21.

[4]刘合财，王雪梅. 积分极限的解法及其应用[J].贵阳学院学报(自然科学版)，2012，7(4)：9-11.

Several Methods to Solve a Classical Sequence Limit Problem

LIU He-cai，CHEN Zhi-you

(College of Mathematics and Information Science , Guiyang University, Guiyang Guizhou 550005, China)

In this paper, four methods are given to solve a classical sequence of number limit problem, i.e., squeezing method, Euler constant method, integral method and experiment method, respectively. Furthermore, general strategies are provided for sequence of number limit problems.

sequence limit; squeezing method；Euler constant method；integral method

2016-03-01

贵州省科学技术基金项目：“函数列的积分中值点的渐近性及其应用”(项目编号：黔科合J字LKG[2013]29号)；贵州省高校优秀科技创新人才支持计划资助项目：“性能退化轨迹模型的失效分布及其参数估计”(项目编号：黔教合KY字[2015]499号)；贵州省科学技术基金项目：“T-凸空间中若干非线性问题的研究”(项目编号：黔科合J字[2014]2005号)；贵州省科学技术联合基金项目：“T-凸空间中集值映射弱Ky-Fan点存在性研究”(项目编号：黔科合LH字[2015]7298号)。

刘合财(1976—)，男，贵州绥阳人，贵阳学院副教授、硕士。主要研究方向：函数论，应用概率统计。

O172.2

A

1673-6125(2016)01-0008-02