埋深对城市地下管道爆炸的影响规律*

牟 杰张金锋黄 武夏一峰汪圣华

1.浙江省安全生产科学研究院 2.浙江省安全工程与技术研究重点实验室

埋深对城市地下管道爆炸的影响规律*

牟 杰1，2张金锋1，2黄 武1，2夏一峰1，2汪圣华1，2

1.浙江省安全生产科学研究院 2.浙江省安全工程与技术研究重点实验室

在特定情况下，城市地下空间废弃管道中会因为油气的泄露等因素形成爆炸环境，利用AUTODYN建立合适的数值模拟模型，围绕管道内部爆炸后对覆盖层的毁伤效应和对地表面空气超压影响展开研究，给埋地管道内部爆炸模拟提供了新的思路。运用建立的模型对不同埋深管道上方覆盖层在爆炸荷载作用下的破坏过程、毁伤规律以及空气中爆炸冲击波的衰减规律进行研究，为建立全面的城市地下管道风险评估指标体系和确定安全防护规范提供了参考。研究结果表明：对于不同埋深管道爆炸，管道上层覆土层的厚度对爆炸后管壁产生的压力影响不大；随着埋深的增加，在空气中形成的伤害破坏范围变小，空气超压衰减符合空气中爆炸后冲击波的衰减规律，埋深每增加0.1m，其空气超压减小4.5%～5.1%左右。

埋地管道爆炸；AUTODYN；数值模拟；安全防护距离

埋地管道在正常运行情况下，管道内部为正压，且助燃物含量低，难以形成爆炸环境。但是在一些特定情况下，由于在城市中存在着大量的市政管道、暗渠等有限空间，易形成爆炸环境空间。本项目研究的主要内容即以此实际存在的特殊定情况为基础，假设在废弃的市政管道中形成了这样的爆炸环境，对于其爆炸的最严重后果进行分析，分析相关因素对于埋地管道内部爆炸后果的影响规律。

1 管道爆炸等效模型

1.1 管道爆炸TNT当量等效可行性分析

目前，对于压力容器的物理爆炸（如蒸汽管道爆炸）和化学爆炸（如可燃气云爆燃）问题，均可采用等效TNT[1]模型计算冲击波超压。等效TNT模型采用能量相当法则，将气体爆炸产生的能量转化为TNT爆炸产生的能量，从而预测爆炸威力。张丽[2]在对工业过程中爆炸破坏效应的计算模型采用TNT当量法分析爆炸的破坏效应；程华瑞[3]等利用TNT当量模型对锅炉爆炸机理进行了研究，计算锅炉爆炸能量和危害半径；刘华东[4]徐慧[5]孔德森[6]等也利用TNT当量法进行爆炸能量，峰值超压的计算和模拟。

1.2 管道爆炸能量计算

采用总能量相同的等效方法，凝聚相TNT质量通过下式计算，首先通过热力学计算得到可燃气体燃烧释放的热量，之后通过下式转化成TNT当量（kg）：

依据此公式可以看出须对气相空间可燃气体爆炸能量进行求解。参考城市燃气管道设计规范[7]的内容，选择了管道直径为600mm，外壁厚10mm的高压（A）型燃气管道，选取20m长度作为数值建模的初始管道模型。假定在一些特殊情况下，泄漏到管道中的可燃气体为甲烷，管道内压力为4MPa，地下空间的内部可以形成封闭爆炸环境，理论上可燃性气体与助燃性气体以化学计量比浓度混合时，爆炸强度最大，故假定氢氧按化学计量比浓度配合。

下面计算的数据将基于上述假设。根据维里气体状态方程可得：

标准状况下，燃气管道发生化学爆炸的反应方程式如下：

CH4+O2→CO2+2H2O-890.31kJ/mol

将甲烷物质的量带入可得到释放的能量为：

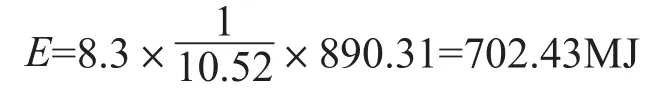
由上面的公式可以得到等效的TNT的量为WTNT=165.22kg。

2 管道爆炸数值模拟模型

2.1 数值模拟模型建立与计算

计算模型是按照1∶1比例建立的三维实体模型，分为空气、土壤、管道、炸药四个单元，土壤计算单元为20m×10m×4m，空气计算单元为20m×10m×14m，管道建立了直径600mm长度为20m的壳体单元，炸药计算单元建立底面积为0.04m2，长度为2.4m的TNT炸药源利用软件建立的模型图，如图1。

图1 三维模型图和网格划分图

2.2 不同埋深条件下管道上方覆土层在爆炸冲击作用下变化规律

运用建立的模型对于不同埋深的管道爆炸进行模拟，设置了五组对比实验，埋深（管道中心线到地表面的距离）分别为0.6m、0.8m、1.0m、1.2m、1.4m。图2为管道埋深为1.0m的在管道爆炸后其上方覆土层隆起高度随时间的变化图。

图2 管道上方覆土层随时间变化图

从图2中可以得到，管道上方覆土层隆起首先从等效炸药中心处开始，并随着时间推移沿管道长度方向地表面也出现隆起，最终管道上方地表面最高隆起高度为2.3m。此模型中，因为将气体爆炸等效为一定体积TNT药包放置在管道中心处，中心起爆后，除了沿管道内部长度方向进行作用与传播之外，对管道中心上方覆土层首先受到冲击，先是爆炸冲击波的作用，随后生成的高温高压气体对外做功，冲击波压力作用下管壁沿着爆炸波传播的方向作横向压缩，如果早期运动过程中不发生层裂失效破坏，管壁在这阶段仍会保持整体状态，继续向外产生膨胀运动。膨胀运动使材料单元在环向受拉伸作用，最终发生断裂，同时还对包围管道的土介质压缩，使两者一齐向外扩散运动，爆炸冲击波传播到地表面时，会在界面处形成拉伸作用的稀疏波，此时爆炸冲击波和稀疏波同时作用于覆土层，使其隆起。随着时间的推移，沿管道长度方向爆炸产生的气体和爆炸冲击波的能量逐渐降低，其上方覆土层不会像管道中心处隆起很高。此模型模拟的结果与历次发生的管道爆炸对地表面的毁坏效应相一致。不同的是一般的管道爆炸是可燃气体泄露到一定的密闭空间中发生爆炸，再有可能引起管道内部气体的二次爆炸，此处是假设在管道内形成了密闭的爆炸空间。此模型的建立给埋地管道爆炸模拟提供了新的思路。

2.3 不同埋深条件下空气中爆炸超压变化规律

利用模型中设置的GAUGE点对垂直管道距离地表面1m的空气超压进行记录，以距离管道中心即爆炸点的距离为横坐标，得到下面的不同埋深埋地管道爆炸后地表面空气超压随距离变化图，如图3。

图3 空气中超压随距离变化图

从图3中可以看出，在垂直于管道地表面方向上，超压大小随着埋地管道深度的增加而减小，离管道中心的等效炸药越近超压下降得越快，随着距离的增加，衰减趋于平缓，但是不同埋深管道爆炸后在空气中超压下降趋势一致。埋深为0.6m的管道爆炸后地表面产生的空气超压最大，埋深为1.4m的管道爆炸后在地表面产生的空气超压最小，因为管道上方覆土层的存在，管道爆炸后产生的冲击波能量和爆炸生成气体的能量经过土壤层的吸收衰减才能传播到地表面，在空气中形成超压，埋深越深爆炸后释放到空气中的能量越少，这也符合一般认知规律，下面对其影响范围和程度的规律进行了研究。

利用超压场分布可以预测埋地管道爆炸的超压作用范围。根据已有的实验模拟数据，可分别获得不同埋深垂直管道竖直方向上距离上峰值超压的最小二乘拟合函数，其表达通式为：

式中：

∆P—垂直埋地管道地表面以上竖直方向对应的峰值超压，MPa；

R—距离，m；

M—等效炸药质量，kg；

a、b和c—拟合常数。分别对五组不同深度管道数值模拟得到的数据进行拟合。

众所周知，人员和设备在冲击波作用下将受到不同程度的伤害和破坏作用，对人员的伤害范围可以根据人员在超压下致死或死亡的概率进行描述，对建筑物的危害范围可以使用侧向超压峰值估算爆炸的破坏程度，因此为明确不同超压范围，选取0.02MPa、0.03MPa、0.05MPa、0.1MPa临界值作为计算依据，以埋深0.6m的超压拟合图为例，得出上述临界值对应的临界距离，如图4所示，其他四个埋深同样的做法，结果如下表。

表 不同深度对应的破坏距离

从上表可以看出，在此假设情况下，随着埋深从0.6m到1.4m，其伤害距离逐渐变小，不同临界值对应的临界距离分别减小40.8%、38.2%、36.1%、35.8%。

图4 埋深0.6m空气超压拟合图

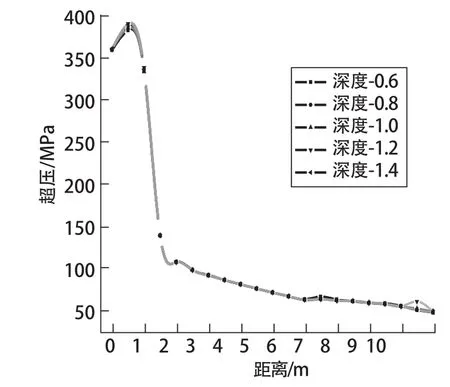
图5 不同埋深管壁压力随距离变化图

2.4 不同埋深条件下管道爆炸后管壁压力变化规律

在模拟过程中从起爆中心开始沿着管道的方向每隔0.5m设置了一个观测点，用来记录管壁在爆炸后受到的压应力，图5为5组不同埋深管道爆炸后在管壁产生的压力随距离变化的点图。从图中可以看出，不同埋深的管道爆炸后管壁所受的压力几无差别，说明管壁所受压力大小主要与内部炸药爆炸有关，与管道上方覆土层的厚度。管壁受到的压力随着与起爆点距离的增加先增大后迅速减小最后趋于平缓。这个变化过程是与模拟所做的假设相一致的爆炸能量首先叠加，在1m产生最大压力外，后随反应完成，压力迅速下降。

3 结论

在一定假设简化条件下，利用ANSYS软件中的WORKBENCH和AUTODYN模块建立了埋地管道爆炸模型，并从理论、相关文献中的实验对比和模拟结果上说明了此模型的合理性，对于埋地燃气压力管道的数值模型的建立提供了新的思路，为管道安全性评估与设计提供了参考。主要得到下面几个方面的结论：

（1）利用TNT当量法作为假设来进行埋地管道爆炸数值模拟是一种可行的方法，通过分析结果来看能够有效地模拟埋地管道爆炸产生的破坏后果。

（2）对于不同埋深管道爆炸，管道上层覆土层的厚度对爆炸后管壁产生的压力影响不大。此模拟结果中，爆炸中心附近隆起高度最大，破坏程度最严重，沿管道长度方向地表面会在爆炸能量作用下发生一定程度的隆起。

（3）随着埋深的增加，在空气中形成的伤害破坏范围变小，空气超压衰减符合空气中爆炸后冲击波衰减规律，埋深每增加0.1m，其空气超压减小4.5%～5.1%左右。

[1] 张楠.埋地管道爆炸对水泥混凝土道路的毁伤效应[D].江苏：南京理工大学,2013

[2] 张丽,何天平.工业过程爆炸事故模式及其破坏效应探讨[J].中国安全科学学报,2007,17(1)：40-45

[3] 刘华东.立式多层长圆筒容器气相区化爆压力波传播及壳体动态响应研究[D].山东：山东大学,2013

[4] 程华瑞,栗继祖.运用TNT当量法及事故树法在分析锅炉爆炸的危害[J].太原理工大学学报,2013,44(3)：361-365

[5] 徐慧,杨靖海,胡云昌.可燃气体爆炸压力下海洋平台舱室围壁变形及破损计算[J].天津大学学报,2000,33(5)：549-552

[6] 孔德森,张伟伟,孟庆辉,门燕青.TNT当量法估算地铁恐怖爆炸中的炸药当量[J].地下空间与工程学报,2010, 6(1)：197-212

[7] 国家建设部.GB50028-2006,城镇燃气设计规范[S].北京：中国建筑工业出版社,2006

[8] 杨冬梅,王晓鸣.混凝土中爆炸数值仿真算法研究[J].爆炸与冲击,2005,2(6)：69-72

[9] Hong Hao,Yaokun WU,Guowei Ma,Yingxin Zhou. Characteristics of Surface Ground Motions Induced by Blasts inJointed Rock Mass[J].Soil Dynamics and Earthquake Engineering,2001,(21)：85-98

浙江省公益技术研究社会发展项目（2014C33046）；浙江省科技厅培育创新载体（2015F10006）