基于通用滞回模型的GMA加工系统滑模变结构控制
李 莹, 欧阳名三, 王西伟,谢 翔,顾冬梅
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
基于通用滞回模型的GMA加工系统滑模变结构控制
李 莹, 欧阳名三, 王西伟,谢 翔,顾冬梅
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
作为精密加工的核心驱动源—超磁致伸缩致动器(GMA)具有推力大、应变大、响应快等优点;然而超磁致伸缩材料的滞回特性阻碍了超磁致伸缩致动器的广泛应用。基于物理或数学方法建立的超磁致伸缩滞回模型都比较复杂,具有强非线性,很难结合到控制器的设计中。本文从控制器的设计角度与GMA的应用环境出发,建立了超磁致伸缩滞回通用模型;并采用基于线性反馈的滑模变结构控制方法设计控制器;理论及仿真结果证明并验证了此方法的有效性。
GMA;滞回通用模型;滑模变结构控制;线性化反馈
作为精密加工核心驱动源的超磁致伸缩致动器(GMA),具有推力大、应变大、响应快及分辨率高等优点,是超磁致伸缩材料(GMM)的重要应用领域之一。然而,由于GMM的非线性滞回特性,给GMA的建模与控制造成了极大的困难。GMM滞回模型的建立以及如何消除滞回并设计合理的控制器成为研究的热点。目前,GMM滞回模型主要采用J-A模型[1-3]、P-I模型[4-5]及自由能模型[6-7]。对GMA的控制主要采用两种方式,一是前馈反馈控制方法,构造GMA滞回逆模型作为前馈控制器,然后根据偏差设计主控制器,使系统输出满足精度要求;二是直接控制方法;采用非线性控制方法,如模糊控制、神经网络控制保证系统的跟踪误差限制在一定范围内[8-9]。
基于物理及数学原理建立的GMM滞回模型都比较复杂,具有强非线性,很难将模型结合到控制器的设计中。本文从控制角度和GMA的应用环境出发,文献[10]建立了GMM通用滞回模型;并根据所建模型特点采用线性反馈的滑模变结构控制方法。
1 滞回模型
滞回系统的通用模型如(1)式
M(t)=khH(t)+d(H)
(1)
式中:M(t)为GMM由输入磁场产生的总磁化强度;H(t)为激励磁场;kh为最大磁化强度随激励磁场幅值变化系数;khH(t)为模型的线性部分;d(H)为不确定非线性部分。
由文献[11]知,GMM滞回曲线随激励磁场的变化曲线如图1所示。
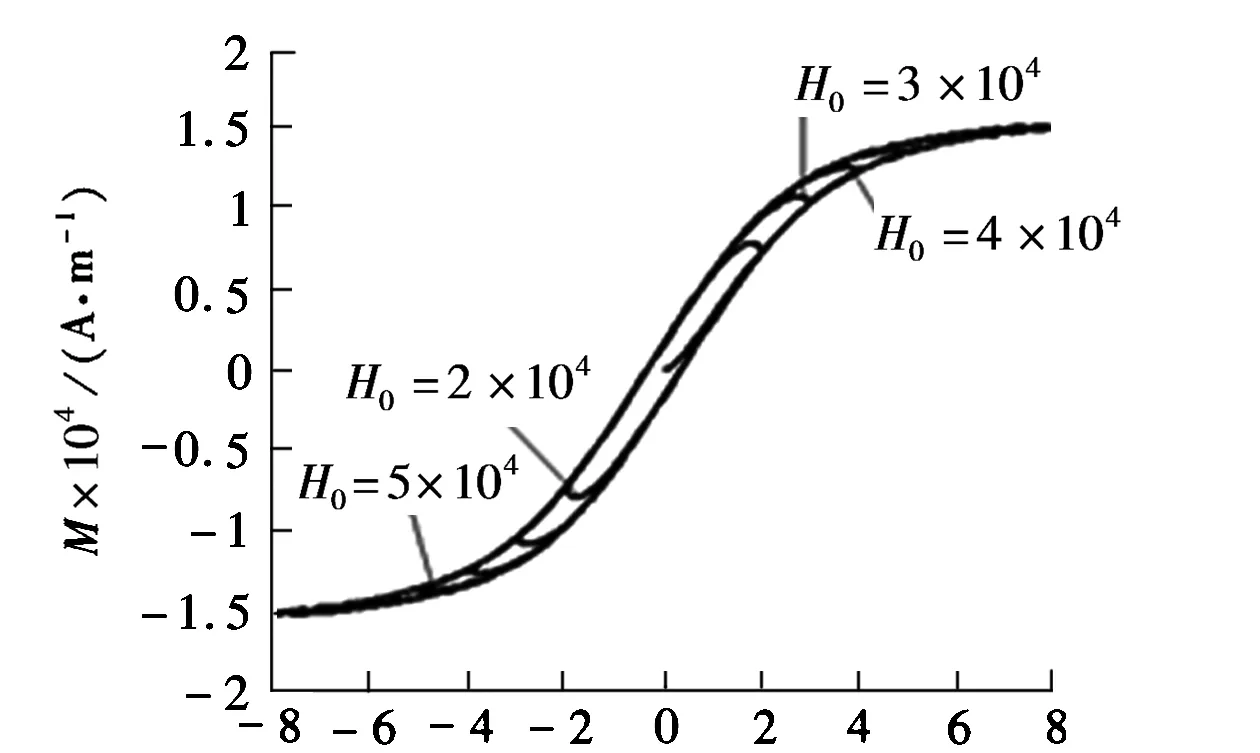
H×104/(A·m-1)图1 滞回曲线随激励磁场幅值的变化曲线
由图1知,H0与1/kh的关系图如图2所示。
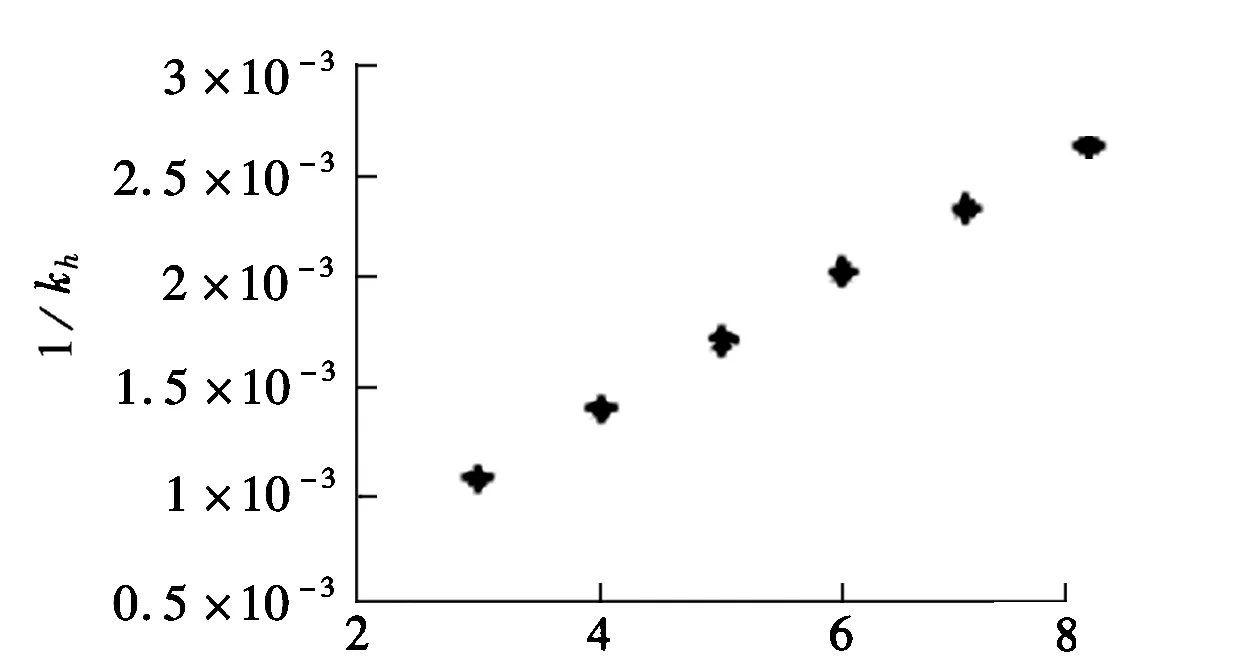
H0×104/(A·m-1)图2 H0与1/kh的关系图
由图2知,H0与1/kh成线性关系,由曲线拟合得
(2)
在受到参数摄动和外干扰时,由于滑模变结构控制具有时不变性,因此不必建立d(H)的精确数学模型,只需求出上界。
如图3将直线AOB右平移,与上行曲线BCA相交于点C,移至直线CD,并且和平行轴相交于点D。过点D作垂线与直线AOB相交于点E。则|DE|为直线AOB到曲线BCA的最大距离,记为dup max=|DE|。同理得到ddown max为d(H)在左平移方向的最大值。则d(H)的上界为d=max{dup max,ddown max}。
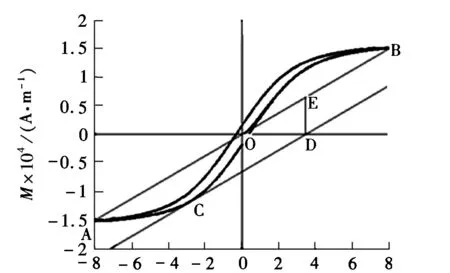
H×104/(A·m-1)图3 滞回曲线
2 GMA动力学模型的建立
由文献[11]知,用于非圆型面车削加工的超磁致伸缩换能器输出端运动微分方程为
α1X2(t)+α2X3(t)+ksu0+EHAλ(t,L)=0
(3)
式中:f为进给量,L与A分别为棒长度与横截面积,EH为棒在磁场下的弹性模量,X(t)为输出端轴向位移,α1与α2分别为预压弹簧非线性刚度系数,m为超磁致伸缩换能器等效质量,k为换能器等效刚度,c为换能器等效阻尼系数;m=mD+mL,c=cD+cL,mL和mD分别为超磁致伸缩棒及换能器输出端的等效质量,cL与cD分别为换能器外阻尼系数与超磁致伸缩材料内阻尼系数,kL与ks分别为超磁致伸缩棒与弹簧的线性部分的刚度,预压力为ksu0。
其中,λ(t,L)为超磁致伸缩棒的磁致应变
(4)
式(4)中基于偏置磁化强度M0,线性化磁化强度M(t,x),可得[12],
(5)
联立式(1)、(5),并带入(3)得
(6)
其中
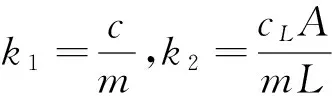
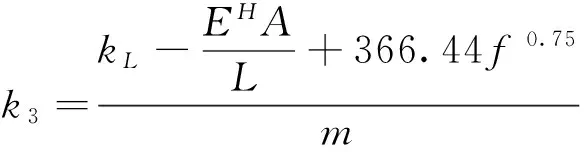
3 滑模变结构控制器的设计
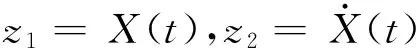
(7)
3.1 线性反馈方法
控制器的设计目的是采用滑模变结构控制设计控制量H(t),使输出GMA输出端位移X(t)跟踪刀头的位置指令。
由式(7)得
(8)
(9)
令
(10)
则系统线性化为
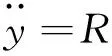
(11)
3.2 滑模变结构控制器的设计
设位置指令为yd,则跟踪误差为
e=y-yd=z1-yd
(12)
定义滑模面为:
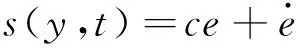
(13)
根据线性化反馈控制律,将滑模控制律设计为
(14)
R=ξ1-ηsgn(s)
(15)
稳定性证明:
定义Lyapunov函数为
(16)
则
=s(-ksgn(s))
≤0
(17)
4 仿真分析
根据所要求非圆型面的加工数据,并通过曲线拟合,得出期望加工进给量的曲线如图4所示。
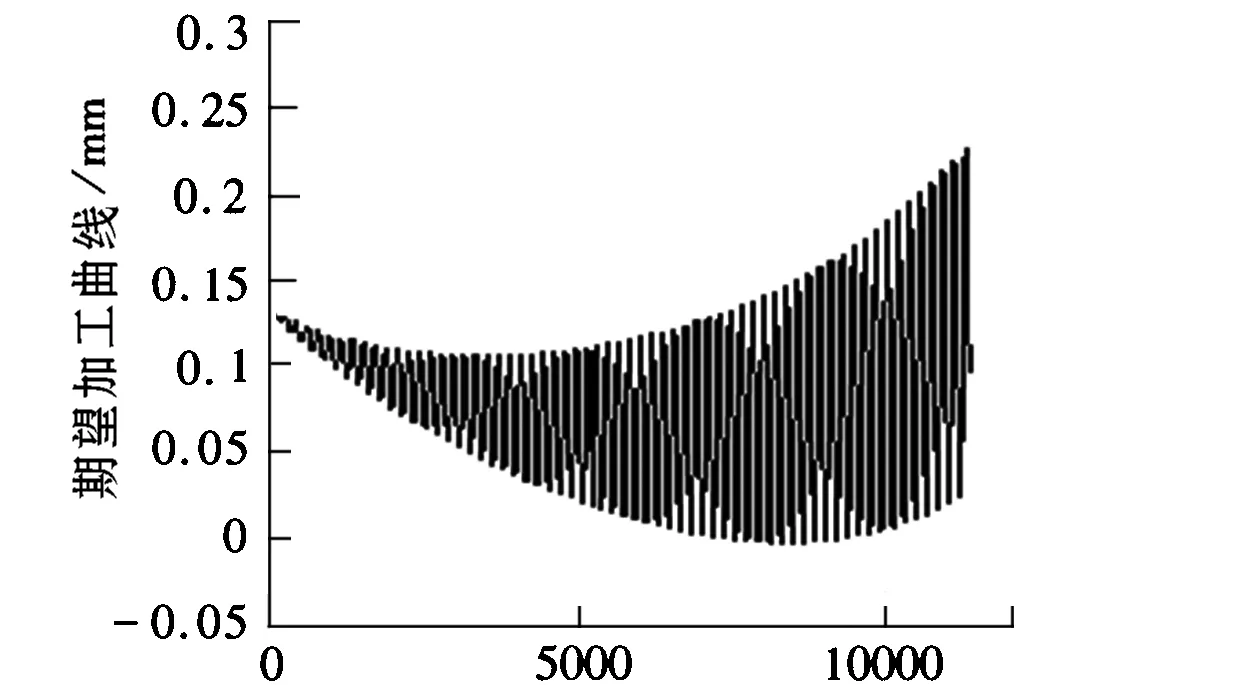
步长图4 期望加工曲线
系统参数的选取见文献[11],由仿真图5可知,系统的响应速度快,跟踪误差在允许的范围内,精度达10-6;由图6知,系统的相轨迹经过短暂的抖振收敛到零,因此可忽略抖振给系统带来不良的影响,满足工程要求。
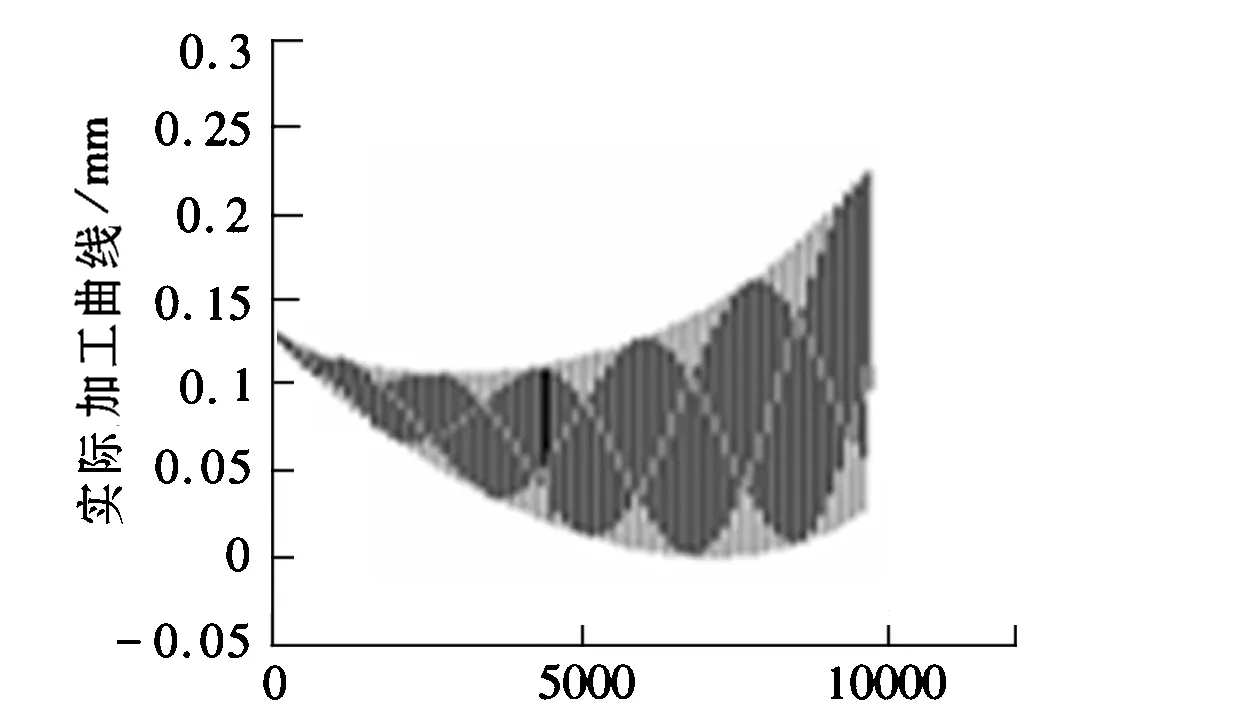
步长a.实际加工进给量变化曲线
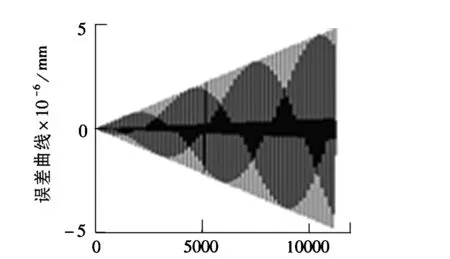
步长b.误差曲线图5 仿真图
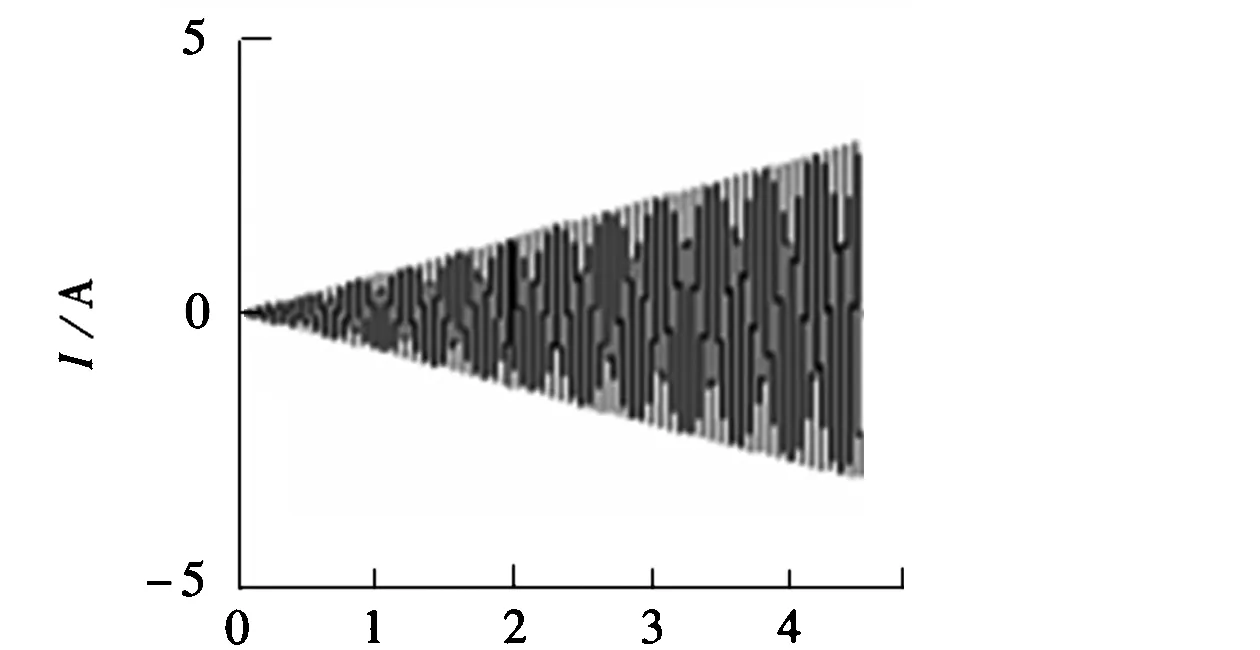
步长a.控制电流的变化曲线
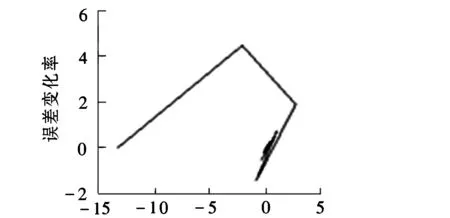
误差×10-4/mmb.相轨迹图6 仿真图
5 结论
本文从控制角度,建立了超磁致伸缩材料的滞回通用模型;将滞回模型等价为线性已知部分和未知有界的非线性部分。一方面克服了建立精确超磁致伸缩滞回模型的困难;另一方面根据通用模型建立的基于线性化反馈的滑模变结构控制器,设计简单,具有很强的鲁棒性。Simulink仿真结果表明,该系统具有较强的克服干扰能力,较快的响应速度,跟踪精度较高,误差精度达到10-6,满足工程需要,为GMA在精密加工中的控制提供一定的理论依据。
[1] 袁惠群,孙华刚.超磁致伸缩材料磁滞回非线性特性分析[J].兵工学报,2009,20(2):180-183.
[2] 郑加驹,王洪礼,曹淑瑛. 超磁致伸缩驱动器频率相关的动态磁滞模型[J].机械工程学报,2008,44(7):38-44.
[3] YING SUN,BOWEN WANG,WENMEI HUANG,LING WENG,et al. Hysteresis Compemsation Control Algorithm for the Giant Magnetostrctive Actuators[J]. Proceedings of the 2006 IEEE International Conference on Mechatronic and Automation,2006:25-28.
[4] XINGSONG WANG,YAN MAO,XIANGJIANG WANG,et al. Adaptive Variable Structure Control of Hysteresis in GMM Actuators Based on Prandtl-Ishlinskii Model[J]. The 33rd Annual Conference of the IEEE Industrial Electronics Society,2007,Taipeo,Taiwan.
[5] 冯颖,胡跃明,苏春翌. 基于Prandtl-Ishlinskii模型的一类回滞非线性系统自适应控制[J].自动化学报,2006,32(3):451-455.
[6] SMITH RALPH C,DAPINO MARCELO J,SEELECKS,STEFAN.Free energy model for hysteresis in magnetostrictive[J].Journal of Applied Physics,2003:458-466.
[7] 田春,汪鸿振.超磁致伸缩执行器的自由能磁滞模型的优化算法研究[J].中国机械工程,2005,16(1):24-27.
[8] 李欣欣,王文. Jiles-Atherton 模型的超磁致伸缩驱动器磁滞补偿控制[J]. 光学精密工程,2007,15(10):1 558-1 563.
[9] CAO SHU-YING, ZHENGJIA-JU, WANG BO-WEN, et al. Precision Position Control for Giant Magnetostrictive Actuator Based on Dynamic Recurrent Neural Network [J]. Proceedings of the CSEE,2006:106-111.
[10] 李莹. 超磁致伸缩微致动器车削加工系统模糊自适应精密位移控制[J].力控制理论与应用.2014,31(2):10-15.
[11] 李莹,袁惠群,吴文波. 超磁致伸缩微致动器车削系统的动力学分析[J].东北大学学报,2012,33(11):1 616-1 619.
[12] 李莹. 超磁致伸缩微致动器驱动的车削加工系统建模与控制[D]. 东北大学,2013.
(责任编辑:李 丽,范 君)
The Sliding Mode Variable Control for Non-circular Cutting Giant Magnetostrictive Actuator Based on General Hysteresis Model
LI Ying,OU-YANG Ming-san,WANG Xi-wei,XIE Xiang ,GU Dong-mei
(School of Mechanical Engineering and Automatization, Anhui University of Science and Technology,Huainan Anhui 232001,China)
Magnetostrictive actuator(GMA) , with large strain , high force , nanometer solution , is the core driver source in the super-precision tracking system. However, magnetostrictive material exhibits dominant hysteresis, which impedes its application . Based on hysteretic Physical or Mathematical theory, the complex hysteretic model with nonlinear is very difficult to be combined with design controller. Considering the designing of controller, a general model for giant magnetostrictive materials is established. Furthermore, sliding mode variable structure control based on linear-feedback is used to design the controller. The theory and simulation results validate the effectiveness of the proposed strategy.
GMA ; common hysteresis model ; sliding mode variable structure control ; linear feedback
2016-01-06
李莹(1982-),女,辽宁葫芦岛人,讲师,博士,研究方向:智能控制算法。
TP273
A
1672-1098(2016)05-0054-05

