基于拟Shannon区间小波的分步小波方法
钟鸣宇,朱宗玖
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
基于拟Shannon区间小波的分步小波方法
钟鸣宇,朱宗玖
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
用拟Shannon区间小波解非线性薛定谔方程,为数值解提供了又一有力工具。简要分析了分步方法的一般形式,得出了分步小波方法的算法公式。说明了色散算子矩阵是Toeplitz矩阵,分步小波方法的运算量主要来自色散段中Toeplitz矩阵向量积。该方法减小了该Toeplitz矩阵的存储空间,从而提高了运算速度。以解析解为准,给出了基于拟Shannon区间小波的分步小波方法的相对误差。结果表明,与以往基于Daubeches小波的分步小波方法相比,精确性有了较大提高。
非线性光学;分步小波方法;数值计算;拟Shannon区间小波;对称Toeplitz矩阵
在非性光纤光学中,非线性薛定谔方程具有基础性作用。常用的分步傅里叶方法,利用离散傅里叶变换求解方程。随着小波分析理论研究的深入,利用小波逼近求解非线性薛定谔方程,已引起人们的广泛关注[1-3]。利用小波逼近解各种非线性偏微分方程的过程中,离散化方程的过程中会产生误差。为了消除这种误差,需要使用插值小波。已有的方法主要采用Daubechies小波。然而,由于Daubechies小波及各阶导函数没有解析表达式,导致求解过程较为复杂,且容易引起强烈的边界效应[4-6]。近年来,拟Shannon区间小波作为解非线性方程的有力工具,引起人们的巨大关注[7-9]。该小波的各阶导数都具有解析表达式,且较好的克服了边界效应的影响,提高了数值逼近的精度[10]。已有的结果显示,非线性偏微分方程的数值解在局部有急剧变化时,利用该小波求解显示出巨大潜力。
本文利用拟Shannon区间小波解最基本的非线性薛定谔方程,结果表明该方法适用于求解非线性薛定谔方程。计算Toeplitz矩阵向量乘(TMVP)时,充分利用了刚度矩阵的稀疏性,提高了运算速度。最后,给出了基于拟Shannon区间小波的分步小波方法的数值计算结果,并与基于Daubechies小波的分步小波方法进行了比较,表明基于拟Shannon区间小波的分步小波方法具有很高的精度。
1 非线性薛定谔方程及分步解法
如果光纤损耗被周期放大器补偿,光脉冲的传输可由归一化非线性薛定谔方程描述为
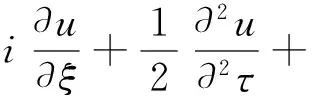
(1)
式中:u、ξ、τ分别为归一化脉冲包络复振幅、归一化距离和归一化时间,可分别表示为
式中:A为脉冲的实际振幅,z为传输距离,t为时间,vg为脉冲群速度,P0为脉冲峰值功率,对双曲正割脉冲,T0=TFWHM/1.76为脉冲初始半宽度,γ为光纤的非线性系数。根据一般的分步方法,式(1)写为
(2)
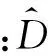
假定在传输的过程中,色散与非线性效应分别作用,可得到其数学表达式为
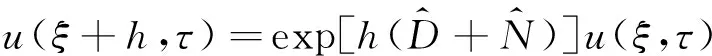
(3)
为提高精度,采用对称分步傅里叶方法
u(ξ+h,τ)=
(4)
当h和τ足够小,精度可以得到保证。
2 拟Shannon区间小波构造
由于Shannon小波不具有紧支撑特性,因此,对Shannon尺度函数进行正则化处理
φσ(τ)=φ(τ)Rσ(τ)
(5)
φσ(x)具有良好的紧支撑性,定义d为均匀离散单元格的大小,则可得到插值核函数为
φσ,d(τ-τn)=
(6)
ωj,n(τ)=ωj(τ-τn)=
(7)
依经验取r=3或r=3.2。
函数u(x)可表示为:uj(τ)=∑uj(τn)ωj(2jτ-n),其逼近误差小于10e-16[10]。在τk处的一阶、二阶导数可表示为
(8)
(9)
3 非线性偏微分方程的拟Shannon区间小波空间离散
如前所述,u(x)可近似表示为
uj(τ)=∑uj(τn)ωj(2jτ-n)
(10)
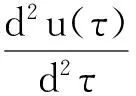
则可把U(xk)的二阶微分表示为
U″(xk)=U(xn)W2(xk-xn)
(11)
一般将矩阵W1和W2称为一阶和二阶微分算子矩阵。求一阶微分的该微分算子矩阵是一般的带状Toeplitz矩阵,二阶微分的微分算子矩阵是对称的带状Toeplitz矩阵。
4 基于拟Shannon区间小波的分步小波方法及运算时间复杂度
各种不同的分步方法中,非线性段的处理方法是完全相同的,不同之处在于如何处理色散段的求导项。基于分步小波方法的色散段可写为
(12)
其中i是虚数单位,完整的分步小波方法可写为
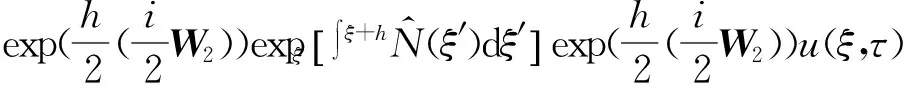
(13)
5 实验结果及分析
为了使计算结果具有通用性,使用式(1)表示的归一化模型,设输入为
u(0,τ)=2sech(τ)
(14)
其计算结果如图1所示。
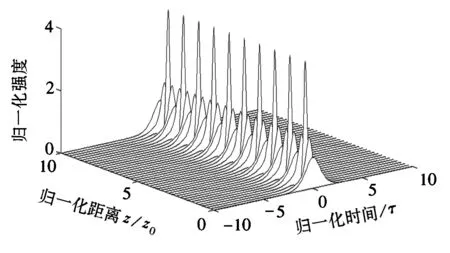
图1 二阶孤子在10个孤子周期上传播
为了更加精确的比较各种数值方法的计算精度,使用式(1)的解析解f(ξ,τ)作为标准[12],解析解的数学表达式为
f(ξ,τ)=u(ξ,τ)=
(15)
基于拟Shannon区间小波的数值解用g(ξ,τ)表示,定义分步傅里叶方法的相对误差为
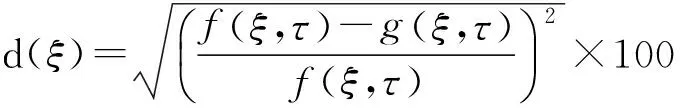
(16)
误差曲线如图2所示,该误差曲线是取样点数为512,1024,2048三条误差曲线的平均值。在40个孤子周期内,对二阶孤子的数值计算,其相对误差在0.1%左右波动,运算精度能比较充分的满足数值计算的要求,而以往的研究结果表明,基于Daubechies小波用于数值计算高阶孤子传播,与分步傅里叶方法所取得的公认值的相对误差在5%左右,对一阶孤子,其相对误差在1.2%左右波动[3]。
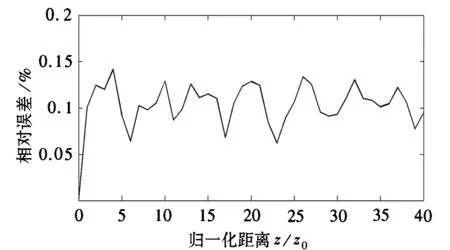
图2 基于拟Shannon区间小波的分步小波方法与解析解的相对误差
6 结束语
本文研究了基于拟Shannon区间小波的分步小波方法解归一化非线性薛定谔方程,分析了其对应的微分算子和色散算子矩阵,基于拟Shannon区间小波比基于Daubechies小波的色散算子矩阵更容易取得。本文使用的分步方法,计算量主要来自色散段中向量与Toeplitz矩阵相乘。简要分析了使用拟Shannon小波,不能使用基于嵌入式矩阵的FFT的快速算法的原因。提高运算速度应充分利用色散算子矩阵的稀疏性。最后,以方程的解析解为准,得到了该方法的相对误差,表明该方法具有很高的精确性,与比以往的小波分步方法相比,误差降为原来的1/10。如果要将本文介绍的方法的运算速度进一步提高,应设法进一步提高TMVP的运算速度。
[1] PIERCE IESTYN, REES PAUL, SHORE K. Alan. Wavelet operators for nonlinear optical pulse propagation[J]. J. Opt. Soc. Am. A,2000,17(12):2 431-2 438.
[2] 陈宏平,王箭,何国光.光脉冲传输数值模拟的分步小波方法[J].物理学报,2005,54(6):2 779-2 783.
[3] 钟鸣宇,刘东风,胡长俊.高阶非线性薛定谔方程的分步小波方法[J].光子学报,2012,41(8):999- 1 003.
[4] 周又和,王记增,郑晓静.小波伽辽金有限元法在梁板结构中的应用[J].应用数学和力学,1998,19(8):697-706.
[5] 骆少明,张湘伟.一类基于小波基函数插值的有限元方法[J].应用数学和力学,2000,21(1):11-16.
[6] 周涛.小波在微分方程数值解上的应用[J].数学理论与应用,2007,27(1):62-64.
[7] WEI G W. Quasi wavelet and quasi interpolating wavelet[J].Chemical Physics Letters,1998,296:215-222.
[8] 万德成,韦国伟.用拟小波方法数值求解Burgers方程[J].应用数学和力学,2000,21(10):991-2 001.
[9] 梅树立,陆启韶,张森文.求解非线性偏微分方程的自适应小波精细积分法[J].计算物理,2004,21(6):523-530.
[10] 黄素清,张森文,邢如义.拟Shannon区间小波的构造及其在数值逼近中的应用[J].中国农业大学学报,2004,9(3):67-70.
[11] 梅树立,马钦,陆启韶,等.小波数值方法及应用[M].北京:科学出版社,2012:79.
[12] AGRAWAL G P. Nonlinear fiber optics,Fourth edition[M].New York:Academic press,2007:135.
(责任编辑:李 丽,编辑:丁 寒)
Split-step Wavelet Method Based Oon Quasi-Shannon Interval Wavelet
ZHONG Ming-yu, ZHU Zong-jiu
(School of Mechanical Engineering and Automatization, Anhui University of Science and Technology, Huainan Anhui 232001, China)
Quasi-Shannon interval wavelet was used to solve the nonlinear Schrödinger equation, which provided another powerful tool for numerical solution of the equation. The general form of split-step algorithm was studied briefly. The dispersion matrix is Toeplitz matrix, and most of the calculation came from Toeplitz Matrix-Vector Product. This method abated the memory space for Toeplitz Matrix to improve calculating speed. Finally, with the analytic solution being the standard, the accuracy of split-step Wavelet method based on Quasi-Shannon interval wavelet was given. The results show that compared with split-step wavelet method based on Daubechies wavelet, the accuracy has improved greatly.
nonlinear optics; split-step wavelet method; numerical analysis; Quasi-Shannon interval wavelet; symmetrical Toeplitz matrix
2015-10-14
钟鸣宇(1982-),男,四川三台人,讲师,硕士,研究方向:光通信系统。
TN929
A
1672-1098(2016)05-0059-04

