轨道交通高架桥结构边界对桥梁结构噪声影响研究

周 力，罗雁云

(同济大学铁道与城市轨道交通研究院，上海 200000)



轨道交通高架桥结构边界对桥梁结构噪声影响研究

周 力，罗雁云

(同济大学铁道与城市轨道交通研究院，上海 200000)

城市轨道交通在给人们出行带来便捷的同时，也给人们的生活带来了一些问题。针对城市轨道交通高架线在车辆运行过程产生的桥梁结构噪声问题，在车辆轨道动力学基础上，以双线单室箱型梁为对象，建立车轮-轨道-桥梁动力学耦合模型，通过模拟真实的车辆运行过程，计算出不同结构边界条件下桥梁在列车经过时的振动情况。建立桥梁声-固耦合模型，通过对比不同结构边界条件下桥梁结构噪声的声场场点声压，发现对桥梁边界进行约束能够降低桥梁结构噪声。

箱型梁；有限元；振动；结构噪声

城市轨道交通作为现代公共交通的重要组成部分，由于其具有准时性、便利性、运量较大且运行基本不受天气条件影响的特点，而逐渐成为大中城市公共交通的骨架。但随着轨道交通的发展，越来越多的问题也开始显现出来，轨道交通在运营过程中产生的振动和噪声便是其中之一。

对于城市轨道交通高架线来说，在运营过程中，主要噪声有轮轨噪声、桥梁结构噪声、集电噪声等。在这些噪声中，桥梁结构噪声往往是被忽略的一部分。原因之一是国内现有的环境评价标准一般采用的计权方式为A计权，但是A计权大大低估了低频噪声，而桥梁结构噪声恰恰属于低频噪声[1]，所以在设计与建设工作中，桥梁结构噪声往往容易被忽略。文献[2]根据相干分析，发现在桥梁下方的区域内，存在很明显的“结构噪声区域”。此外，现有研究表明，低频噪声兼具低频声与噪声的物理特性，加之低频声媒质传播特性以及人耳听觉特性，使之具有不同于其他频段噪声的特殊属性，如：低频声传播距离远，衰减慢；低频声传播时，能够与人体器官产生共振，使人产生不适，心理烦躁等[3]。

目前，城市轨道交通或高速铁路桥梁结构噪声已经引起越来越多学者的关注和研究，并且取得了一定的进展。文献[4]以混凝土简支箱梁为研究对象，根据有限元/边界元理论，建立车-轨-桥耦合模型，将计算出的桥梁振动响应作为桥梁结构噪声模型边界条件，通过声学仿真分析，得到箱型梁各面板声学贡献量，发现箱梁顶板和两侧翼缘板下面板是辐射噪声最大部件。文献[5]以京沪某高铁32m双线箱梁为研究对象，通过现场测试和仿真模拟，发现箱梁结构噪声超出限值，并进一步研究发现增大桥梁刚度和质量可以在一定程度上减小结构振动和声辐射水平；腹板倾角减小至0度时，可有效降低结构噪声。文献[6]通过仿真模拟发现扣件刚度和行车速度对箱型梁结构噪声有较大影响，其中扣件刚度对桥梁结构噪声的影响主要在32Hz以下。文献[7]认为控制连续梁桥90Hz以内的振动，将有效降低结构辐射声压水平，同时分别对桥梁阻尼、支座刚度、车辆荷载等参数对结构振动与噪声的影响进行了研究。文献[8]通过对香港某高架铁路混凝土箱型梁的振动、噪声测试，发现结构噪声主要集中在低频段。文献[9]通过对香港西铁混凝土箱梁进行优化设计，将箱梁的腹板直接置于轨道之下，既降低了箱梁的质量，又减小了结构噪声。

本文以城市轨道交通高架线双线单室混凝土箱型梁为研究对象，借助ABAQUS有限元软件，在动力学原理的基础上，建立车轮-轨道-桥梁动力学耦合模型。通过建立轮-轨耦合，并在车轮上施加大小等于轴重的荷载，来模拟实际运营过程，从而计算出简支和固支(不约束垂向位移)两种不同结构边界条件下箱型梁的振动情况。在此基础上，利用ABAQUS连续性声-固耦合分析，建立桥梁的声-固耦合模型，分析桥梁边界条件对桥梁结构噪声的影响。

1 桥梁振动仿真

车辆与桥梁间的作用是通过轮轨间相互作用实现的。车辆作用于桥梁的荷载通过钢轨、扣件、轨枕传递给桥梁。轮轨间作用力大小和方向取决于轮轨接触几何状态(如钢轨表面不平顺)和轮轨的振动情况。如图1所示，车辆、轨道和桥梁三个子系统通过轮轨耦合作用和桥轨耦合组成整个动力学系统，在系统激励作用下，产生耦合振动，进而引起各部件的振动响应[10]。

1.1 车轮-轨道-桥梁耦合模型

本文并未建立车辆模型，而是通过建立轮-轨耦合，并在轮对上施加大小等于轴重的荷载，来模拟车辆和钢轨间的动力作用。其中，轮对模型的车轮滚动半径R=420mm，采用磨耗型踏面。钢轨有限元模型采用实体单元进行模拟，密度为7 830kg/m3，弹性模量E=2.06×1011Pa，泊松比取0.3。对于作用在钢轨上的移动载荷，只有当移动载荷距离钢轨端部不小于30m时，由模型中钢轨端部边界对计算结果产生的影响才可以忽略不计[11]。因而，本文建立了长度为90m的钢轨，钢轨中部30m与桥梁联接，剩余两端部分则通过弹簧-阻尼单元直接与地面联接。这样保证了在整个计算过程中，车轮距离钢轨端部的最小距离不小于30m。

轮轨耦合的建立是整个车轨桥模型的重点，而研究轮轨耦合作用的关键在于如何正确的求解轮轨间的相互作用力[12]。本文基于轮轨接触的基本理论，采用非线性赫兹接触模型计算轮轨法向接触力，切向摩擦和蠕滑行为则用摩擦系数法描述[13]。其中，赫兹(Herz)非线性接触理论如公式(1)所示

(1)

本文借助ABAQUS有限元软件中的面-面接触，根据式(1)求得不同弹性压缩量对应的轮轨法向作用力，输入到Tabular模型中，从而模拟轮轨法向接触。

轮轨间的切向作用，则根据式(2)进行定义，其中μ取0.25。

F=μP(t)

(2)

式中：F为轮轨间切向作用力，N。

扣件系统是联接钢轨和钢轨以下结构的部件，其作用是将钢轨固定在轨枕上，保持轨距、阻止钢轨爬行。扣件在荷载作用下一般表现为非线性变形，但在模拟中常采用线性单元模拟[14]。本文以普通轨道为研究对象，将扣件系统模拟为线性弹簧-阻尼单元，且只考虑垂向自由度。

由于抗弯、抗扭性能好，外观线型流畅、美观，设计、施工经验成熟，因而，箱型梁在国内轨道交通中得到广泛应用，如上海城市轨道交通6号线。为了真实地反映桥梁结构在列车荷载作用下的振动情况，本文采用三维实体单元，建立了30m单跨双线单室混凝土箱型梁有限元模型，密度取3 000kg/m3，弹性模量为3.45×1010Pa，泊松比为0.17。桥梁横断面几何尺寸如图2所示。由于本文的研究目标为桥梁梁体，为了减小模型的大小且不影响计算精度，所以并未建立桥墩，而是将用来模拟桥梁支座的弹簧-阻尼单元直接与地面联接。

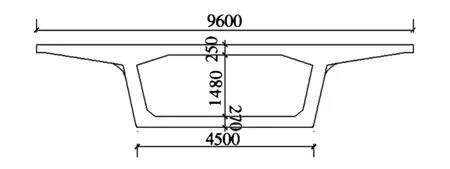
图2 双线单室混凝土箱梁横断面图(单位：mm)

本文建立的车轮-轨道-桥梁耦合模型如图3所示。

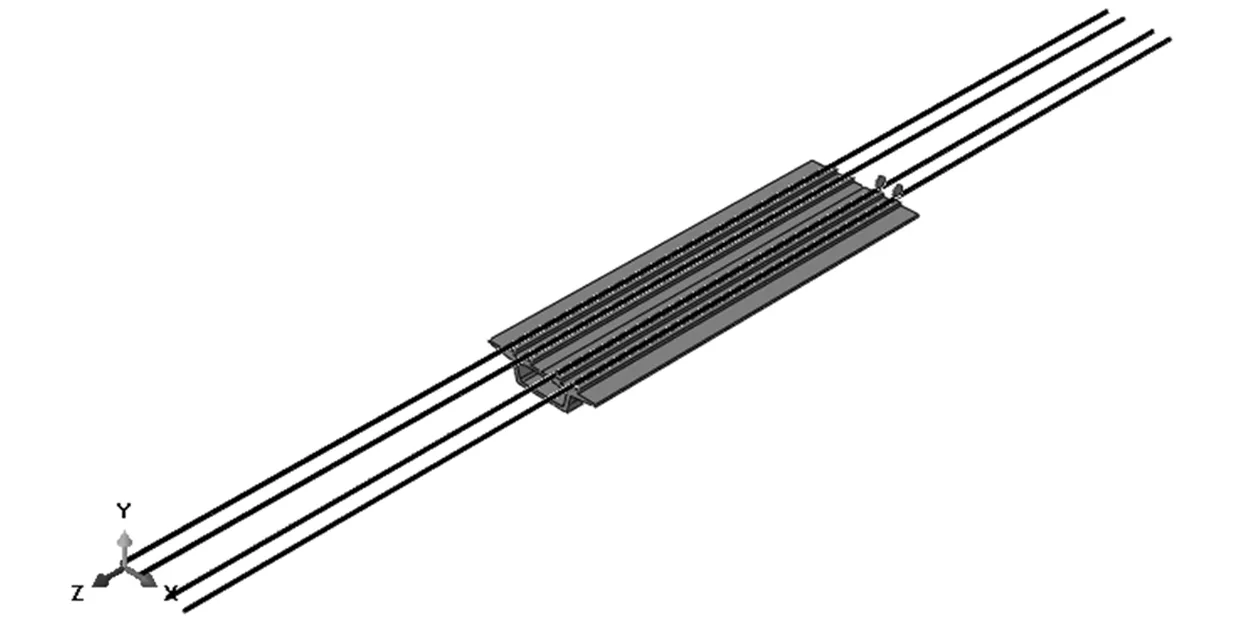
图3 车轮-轨道-桥梁耦合模型

1.2 动力模型计算

本文选择轨道高低不平顺作为系统激励源。其中，轨道不平顺是指实际车轮和钢轨的接触面沿轨道长度方向上与理论平顺的轨道面之间的偏差。轨道结构在长期的列车荷载作用下，由于轮轨间作用产生的轨道累计变形不断增大，形成了各种各样的轨道不平顺如轨道高低不平顺、轨道水平不平顺、轨道方向不平顺等；此外，国内外实测资料表明，轨道不平顺本质上是一个随机过程，在仿真分析中常将其处理为平稳的各态历经的随机过程[15]。由于桥梁振动中主要以垂向振动为主，所以本文选取轨道高低不平顺作为激励源，根据三角级数法，通过MATLAB编程，将美国六级不平顺功率谱，如式(3)，转换为轨道高低不平顺空间样本[16-17]，如图4所示。

(3)

式中：Sv(ω)为轨道不平顺功率谱密度函数，cm2/(rad·m)；ω为空间角频率，rad/m；ωc为截断频率，对于美国六级谱，取0.824 5 rad/m；Av为粗糙度系数，cm2/(rad·m)；K为一般取0.25。

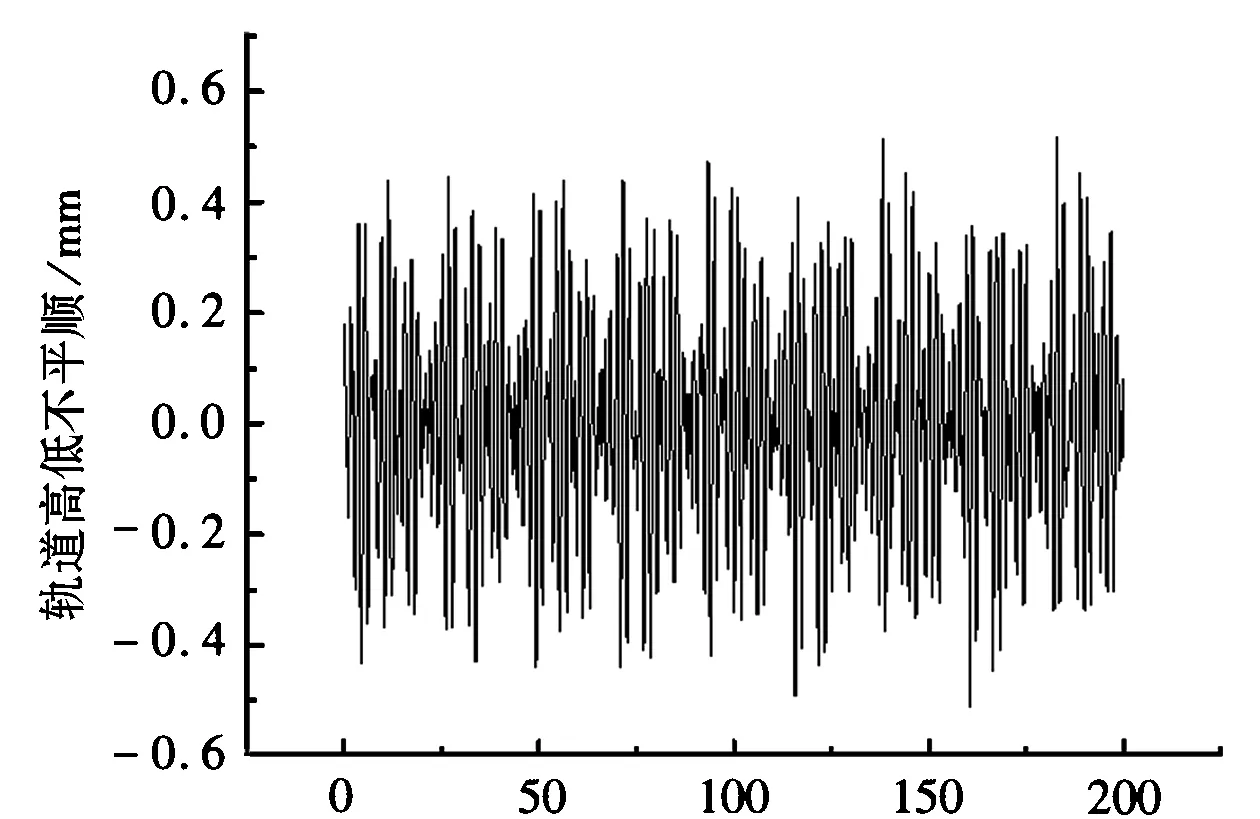
沿钢轨纵向/m图4 轨道高低不平顺空间样本

将模拟出的空间样本，输入到模型中。通过让轮对以60km/h的速度沿着钢轨运动，且在轮对上施加大小等于轴重的荷载来模拟车辆运营时桥梁的振动情况，分别计算桥梁在简支和固支(不约束垂向位移)的边界条件下的振动。其中，简支边界条件下桥梁跨中桥面振动加速度频谱图如图5所示。文献[18]中国内某城市高架桥普通轨道30m双线单室混凝土箱梁振动实测结果表明，桥面振动在低频范围内的主要频率段为：40～80Hz和150～180Hz，其中振动加速度在40～80Hz段的峰值更大，约0.025 m/s2。从图5中看出，仿真模型中跨中桥面振动加速度的主要频率段为25～65Hz，振动加速度峰值为0.02m/s2，在100～200Hz内振动加速度较小。表明建立的动力仿真模型能在一定程度上反映实际的桥梁振动，但存在一些差异。

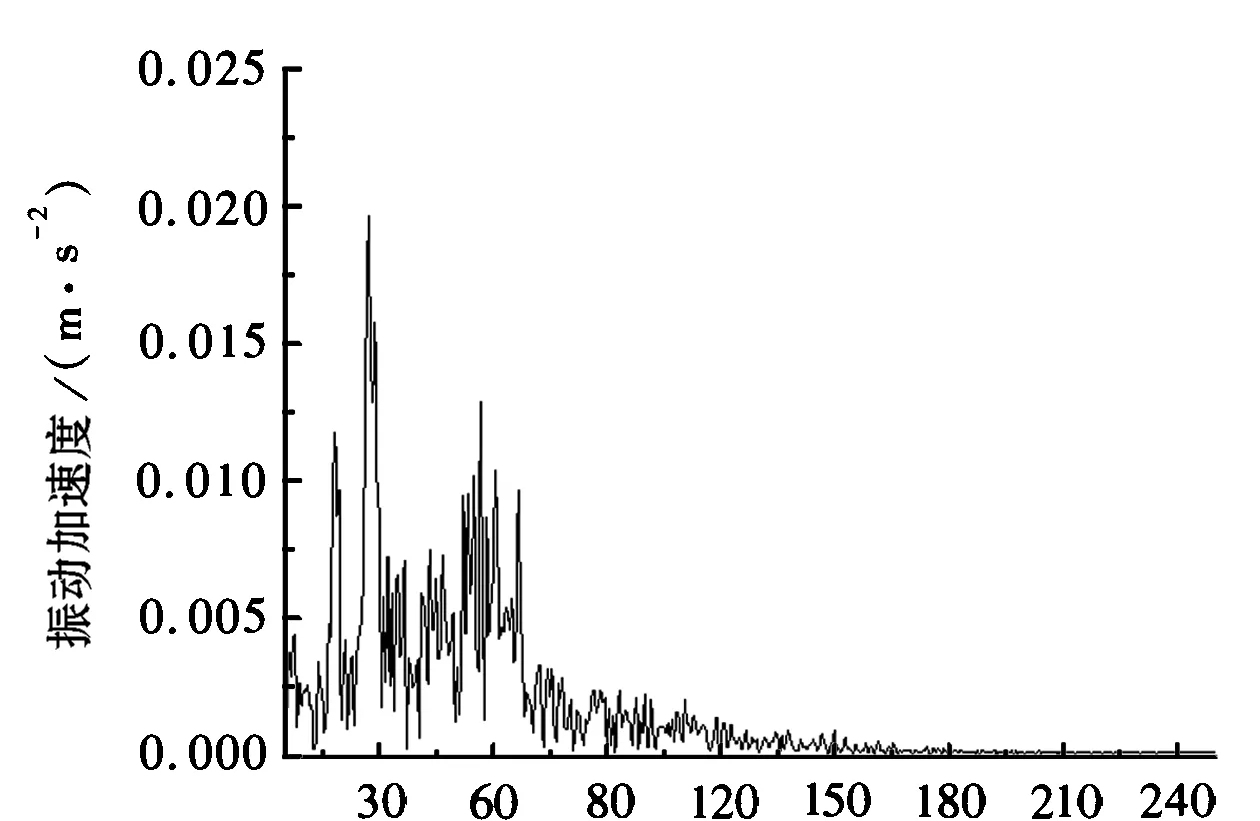
频率/Hz图5 桥梁跨中桥面振动加速度频谱图

2 桥梁声-固耦合仿真分析

声波是一种机械波，是在弹性介质(气体、液体、固体)中传播的压力、应力、质点运动等的一种或多种变化，一定范围的频率和强度的声波作用于人耳就产生了声音的感觉[19]。桥梁结构噪声就是由桥梁结构振动引发周围空气中的介质振动形成的。

由于桥梁与空气间的相互作用为弱耦合，即桥梁的振动容易引起空气介质的振动，而空气中介质振动对桥梁的振动影响非常微弱，所以本文采用弱耦合模型对桥梁结构噪声进行分析。

2.1 桥梁声-固耦合模型

本文利用ABAQUS的声学单元，建立桥梁结构噪声子模型。将计算出的桥梁振动位移结果作为边界条件，映射到桥梁结构噪声子模型当中。由于桥梁结构噪声为低频噪声，频率一般在250Hz以下，而声学网格的尺寸要小于最高分析频率对应波长的六分之一到十分之一，所以模型中声学网格的尺寸取15cm。建立的桥梁声固模型如图6所示。同时，为了保证计算出的声压时域结果在进行频谱分析时能够达到250Hz，根据采样定理，将分析步的增量步设置为0.002s。

图6 桥梁声-固耦合模型

2.2 桥梁结构噪声分析

本文在桥梁结构噪声模型跨中截面选取两个点作为观察点。《环境影响评价技术导则城市轨道交通》(HJ453-2008)中规定距外轨中心线7.5m，距轨面高1.5m的测点为高架线列车运行噪声源强点，所以本文选取近轨侧源强点作为观察点A，同时选取桥梁底板近场点作为第二个观察点B，如图7所示。A点是桥梁振动产生的综合噪声，B点则主要是底板振动产生的噪声[2]。

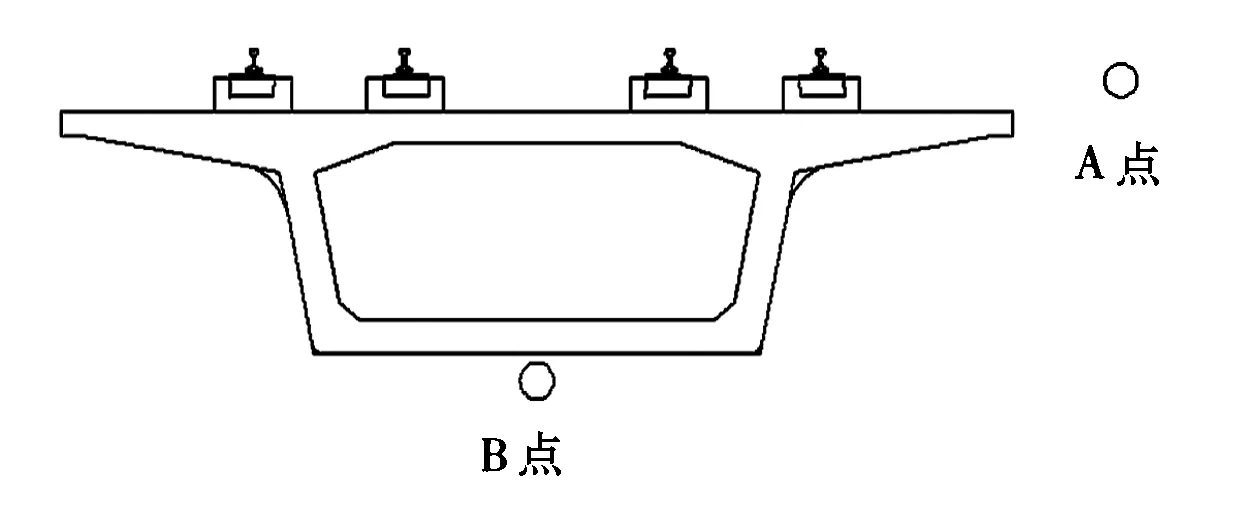
图7 声场观察点示意

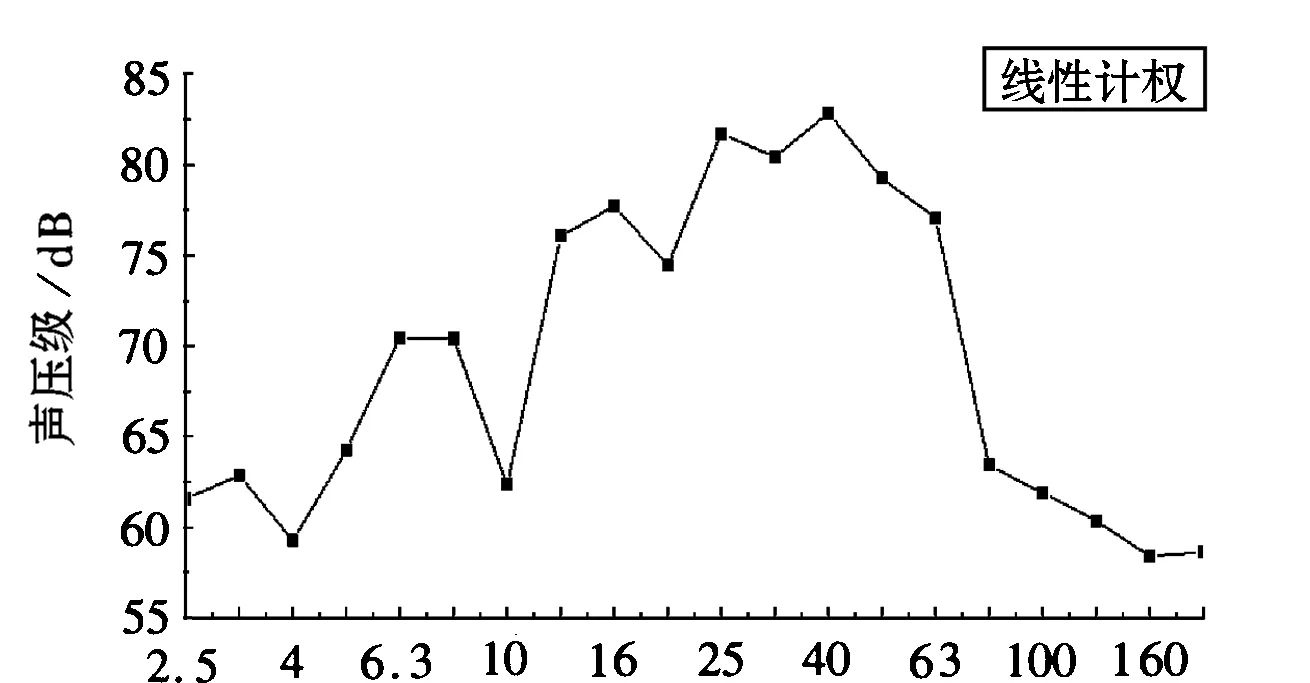
图8为简支箱梁B点处1/3倍频程线性计权声压级频谱图。

频率/Hz图8 B点处1/3倍频程线性声压级频谱图

从图8中可以看出，箱梁底B点处结构噪声的主要频率为12.5～63Hz，最大声压级为84dB。国内某城市高架双线混凝土简支箱梁噪声实测结果表明，在列车运行速度为60km/h的工况下，对于普通轨道-全封闭声屏障，距梁底面0.3m处噪声的主要频率段为40～80Hz，在63Hz处达到最大值85dB，并且该处的噪声可认为主要是桥梁结构噪声[18]。由此来看，本文的模拟结果在一定程度上能够反映实际情况。

改变模型中桥梁边界条件，最终得到桥梁在简支和固支两种边界条件下的结构噪声仿真结果。图9为桥梁在简支和固支(不约束垂向位移)边界条件下，A点噪声声压频谱图。从图9中可以看到，桥梁振动产生的结构噪声主要频率在100Hz以下，且当桥梁边界条件设置为固支(不约束垂向位移)时，桥梁结构噪声明显低于简支梁振动产生的噪声。从图10也可以看出固支(不约束垂向位移)条件下的桥梁结构噪声要小于简支梁振动产生的噪声。

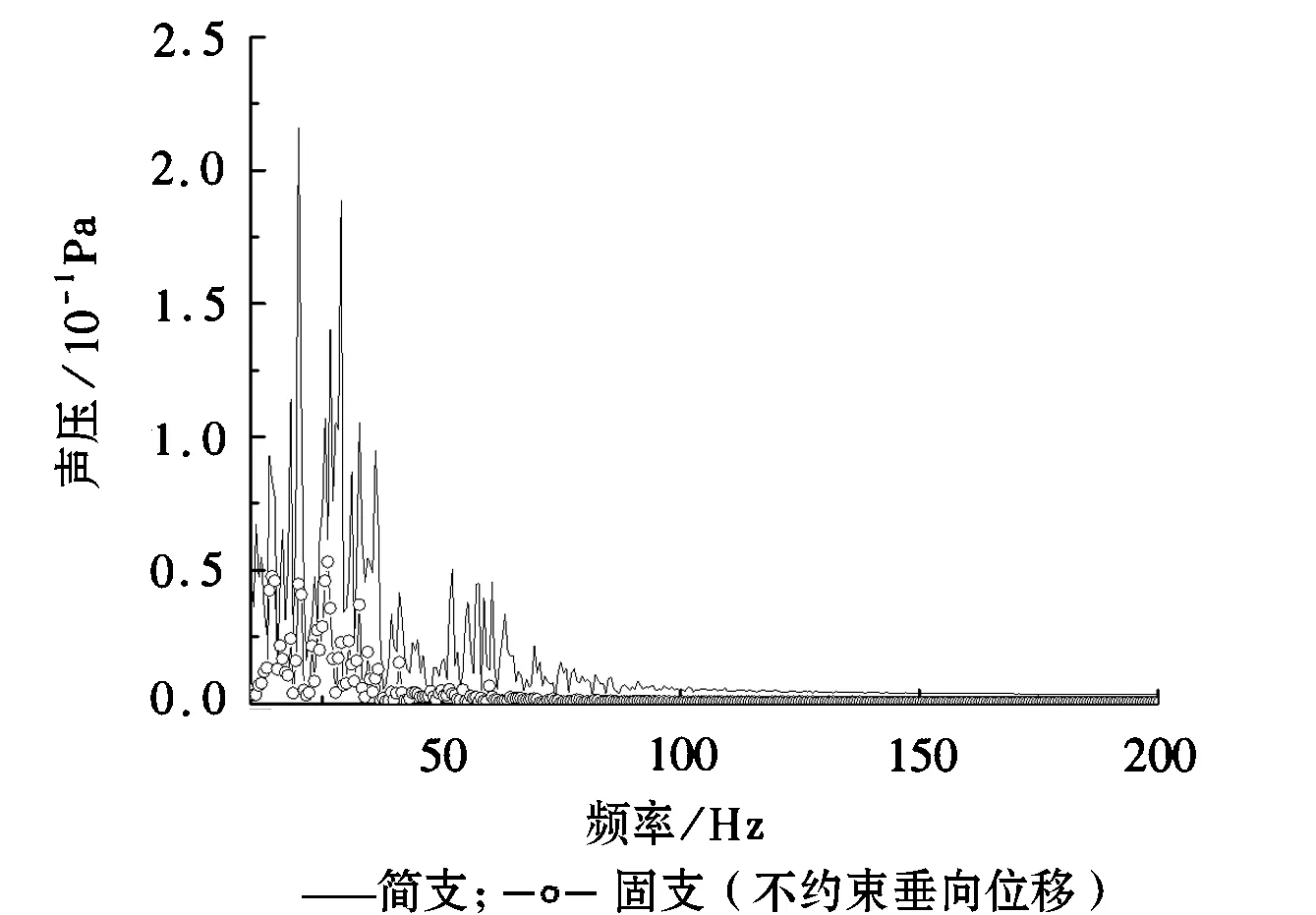
图9 A点声压频谱图

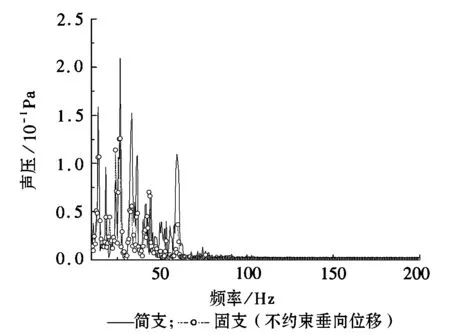
图10 B点声压频谱图

3 结论

在城市轨道交通的设计和建设过程中，为了管理和施工的方便，一般都会采用简支梁作为标准梁，除非在遇到特殊情况，如跨越路口或河流。根据本文的计算结果，可以看出，桥梁在固支边界条件下的结构噪声要低于简支边界条件下的结构噪声。从降低结构噪声的角度来看，单纯采用简支梁并非是一个很好的选择。虽然，桥梁固支会给施工带来诸多不便，且理想的固支边界条件很难实现。但是，可以考虑通过对简支梁的梁端进行加固来降低桥梁结构噪声。

本文在研究过程中也存在一些缺陷，第一，在动力学模型中并未建立完整的车辆模型，而仅以在一对轮对上施加轴重作为荷载，这难免会使得计算出的振动结果与实际情况有出入；第二，声学模型采用的是有限元而非无限元，模型声场截断边界会对计算结果产生影响。所以如果要对本课题进行进一步的研究，可在结合现场实测的基础上，建立更加完善的模型，并研究对梁端进行加固的具体措施。

[1] 张迅. 轨道交通桥梁结构噪声预测与控制研究[D]. 成都：西南交通大学，2012：2-29.

[2] 刘孝寒. 基于相干分析的高速铁路桥梁结构噪声源识别研究[D]. 成都：西南交通大学，2012：32-33.

[3] 闫靓. 低频噪声主观反应客观评价[D]. 西安：西北工业大学，2006：1-3.

[4] 刘林芽，付奇川，邵文杰，等. 箱型桥梁结构的面板声学贡献分析[J].铁道科学与工程学报，2015，12(4)：743-748.

[5] 欧阳昭. 高速铁路桥梁结构噪声研究[D]. 上海：同济大学，2015：18-73.

[6] 石广田， 杨新文， 孙昊天. 双块式无砟轨道-箱梁结构振动与噪声参数分析[J]. 兰州交通大学学报， 2014，33(4)：131-136.

[7] 高飞，夏禾，曹艳梅，等. 城市轨道交通高架结构振动与声辐射研究[J]. 振动与冲击，2012，31(4)：72-76.[8] NGAI K W， NG C F. Structure-borne noise and vibration of concrete box structure and rail viaduct[J].Journal of Sound and Vibration，2002，25(2)：281-297.

[9] COOPER J H， HARRISON M F.Development of an alternative design for the West Rail viaducts. Proceeding of Institution of Civil Engineers[C]//Proceedings of the Institute of Civil Engineers， London，2002：87-95.

[10] 翟婉明，蔡成标，王开云. 高速列车-轨道-桥梁动态相互作用原理及模型[J]. 土木工程学报，2005，38(11)：132-137.

[11] 翟婉明. 车辆-轨道耦合动力学[M]. 北京：科学出版社，2007：131-132.

[12] 康熊. 铁路计算机仿真技术[M]. 北京：中国铁道出版社，2012：45-48.

[13] 南化勇. 路基上CRTSII型板式无砟轨道动力特性分析及参数研究[D]. 兰州：兰州交通大学，2012：36-37.

[14] 刘维宁，马蒙. 地铁列车振动环境影响的预测、评估与控制[M]. 北京：科学出版社，2014：32-35.

[15] 陈冬梅.轨道不平顺数值模拟中的随机数生成算法研究[D]. 上海：复旦大学，2012：16-27.

[16] 雷晓燕. 高速铁路轨道动力学——模型、算法与应用[M]. 北京：科学出版社，2015：116-121.

[17] 陈士军，凌贤长，朱占元，等. 轨道高低不平顺谱分析[J]. 地震工程与工程振动，2012，32(5)：33-38.

[18] 王一干. 城市轨道交通高架桥30m混凝土简支梁结构噪声研究[D]. 北京：中国铁道科学研究院，2015：33-34.

[19] 方丹群，张斌，孙家麒，等. 噪声控制工程学[M]. 北京：科学出版社，2013：28-31.

(责任编辑：李 丽，吴晓红，编辑：丁 寒)

Research on the Influence of Structural Boundary of Rail Transit Viaduct on the Structure-Born Noise

ZHOU Li, LUO Yan-yun

(Institute of Rail Transit, Tongji University, Shanghai 200000, China)

Urban rail transit improves people's life, but meanwhile brings some problems. Aiming at the problem of the bridge structure-born noise caused by the urban rail transit, the wheels-rail-bridge coupling system was built basing on vehicle-track dynamics theory, and then the vibration level of box girder with different boundary conditions could be achieved in the simulation model. On this foundation, the acoustical-structure coupling model was established. It is found that the constraint of bridge boundary can reduce the structure noise level by calculating the sound field of bridge structure noise under different boundary conditions.

box girder; finite element; vibration; structure-born noise

2016-08-29

周力(1989-)，男，安徽阜南人，在读硕士，研究方向：轨道交通振动与噪声控制。

U24；TB123

A

1672-1098(2016)05-0020-05