谈“极限”思想及其求速度加速度的应用

肖 文

(望江县第二中学 安徽 安庆 246200)

陈 泽

(江苏省盐城中学 江苏 盐城 224005)



谈“极限”思想及其求速度加速度的应用

肖 文

(望江县第二中学 安徽 安庆 246200)

陈 泽

(江苏省盐城中学 江苏 盐城 224005)

结合物理学科知识，介绍了物理学中的“极限”思想，并通过运动学中的两个典型例题,详细分析了“极限”思想求解物体的瞬时速度、瞬时加速度的方法与思路.这种方法只需要学生具备初等数学的知识，就能加深对物理量瞬时值的理解；同时，对学生今后学习导数的概念也具有重要的启发意义.

极限思想 运动学 瞬时值

在高中物理学习过程中,经常遇到求解物体的瞬时速度、瞬时加速度(通常简称速度、加速度)的问题，但多数都集中在匀变速直线运动中，因而可以应用匀变速直线运动的基本公式、牛顿第二运动定律来求解，这属于典型的动力学问题的求解思路.还有一些则是非匀变速运动的问题，通常应用“微元法”、“矢量分解法”来求解，这种方法的过程较为复杂，也很难使学生真正地理解，针对这种方法的难理解性，很有必要寻找其他思想方法来解决这一问题.而“极限”思想求解物体的速度、加速度虽然过程略显复杂，但由于具有较强的数理逻辑性，也更符合高中学生的认知，因此，相对而言更容易被学生理解；从本质上讲，“极限”思想求解物体的速度、加速度立足于速度、加速度的原始定义，因此，这种思想方法对于深入理解速度、加速度的概念是非常重要的；另一方面，这一方法涉及的数学知识也是中学生物理竞赛要求掌握的数学基础知识[1].

以下将结合物理学科知识，介绍物理学中的“极限”思想，着重就运动学中的两个典型例题，详细分析、介绍 “极限”思想求解物体的速度、加速度的方法与思路.

1 物理学中的“极限”思想

理解了“极限”思想，非常有利于深化对物理概念的认识与理解，对于什么是瞬时速度、什么是瞬时功率这样的问题，也许不少学生会熟练地回答：物体在运动过程中某一时刻或某一位置时的速度；力与物体的瞬时速度的乘积.由此可见，学生对瞬时速度还是停留在字面上的理解，而对瞬时功率的理解则是“翻译”了公式“P=Fv”，从本质上讲，学生并没有真正理解这些概念[2].

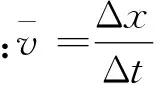
由此可见，某一时刻的瞬时速度就是包含该时刻的极短时间间隔内的平均速度在Δt→0时的极限.在实际的物理问题中，这样的极限当然是存在的，可能还有学生会问，Δt→0时，则Δx→0，这样的比值到底是什么呢？学生提出这样的疑问应该值得肯定，说明学生已经深入思考过这个问题， 对于Δt→0时，则Δx→0这样的结论是完全正确的，但两者趋向于零的速率未必是相同的.举例来说，如

x(t)=kt

则

Δx=k(t+Δt)-kt=kΔt

那么Δx趋于零的速率是Δt→0的k倍，再如

x(t)=kt2

Δx=k(t+Δt)2-kt2=2ktΔt+kΔt2

忽略二次项kΔt2，则

Δx=k(t+Δt)2-kt2=2ktΔt

同理也可以用“极限”思想来定义瞬时加速度与瞬时功率，即

上面两个公式分别表示：物体在某一时刻的瞬时加速度(简称“加速度”)就是包含该时刻的极短时间间隔内的平均加速度在Δt→0时的极限；外力在某一时刻的瞬时功率(简称“功率”)就是包含该时刻的极短时间间隔内的平均功率在Δt→0时的极限.对于瞬时功率的定义式还可以进一步写为

若F与v方向相同时，cosθ=1，P=Fv(v为瞬时速度).

在物理学中，还有许多含时间t的物理量，往往都是先从平均值谈起，只有当Δt→0时的极限才是对应的该物理量的瞬时值.采用类比的思想，还可得到某一时刻的角速度、电流、感应电动势的瞬时值.表1为中学物理中常见物理量的瞬时值的定义.

表1 高中物理中应用“极限”思想定义的常见物理量瞬时值一览表

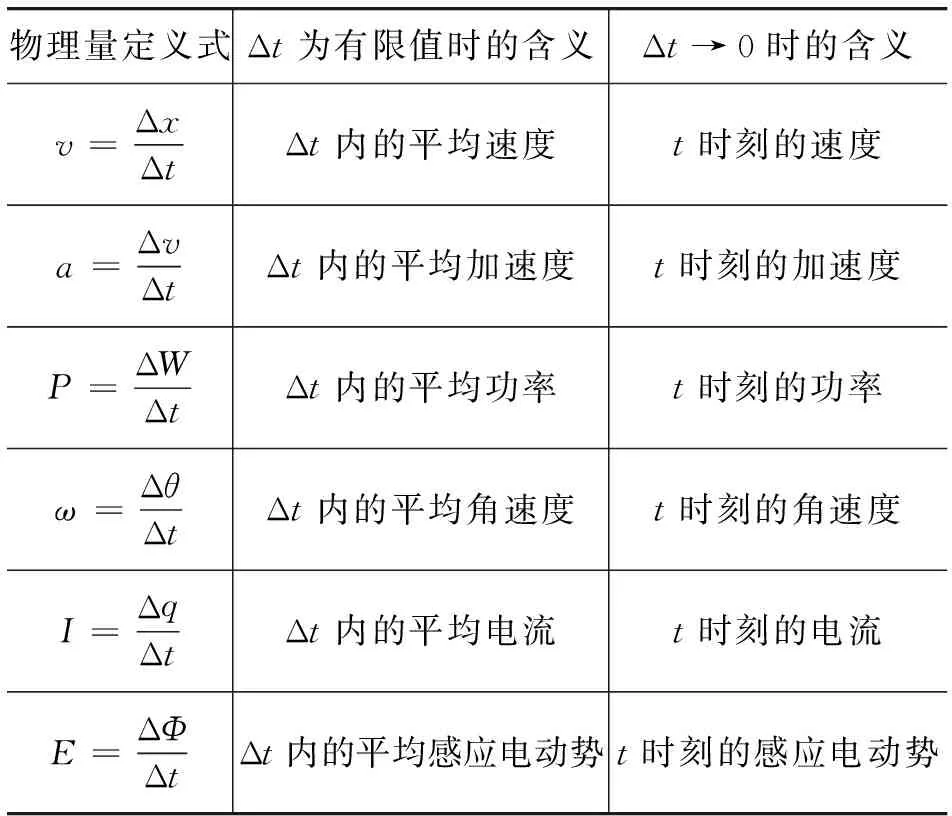
物理量定义式Δt为有限值时的含义Δt→0时的含义v=ΔxΔtΔt内的平均速度t时刻的速度a=ΔvΔtΔt内的平均加速度t时刻的加速度P=ΔWΔtΔt内的平均功率t时刻的功率ω=ΔθΔtΔt内的平均角速度t时刻的角速度I=ΔqΔtΔt内的平均电流t时刻的电流E=ΔΦΔtΔt内的平均感应电动势t时刻的感应电动势

2 “极限”思想求速度和加速度的应用

2.1 滑轮组和绳类连接体问题

【例1】如图1所示，滑轮组由3个尺寸完全相同的小滑轮与一尺寸较大的大滑轮组成，物体A和B分别具有向下的加速度aA和aB，物体C具有向上的加速度aC，求aA，aB，aC之间的关系.

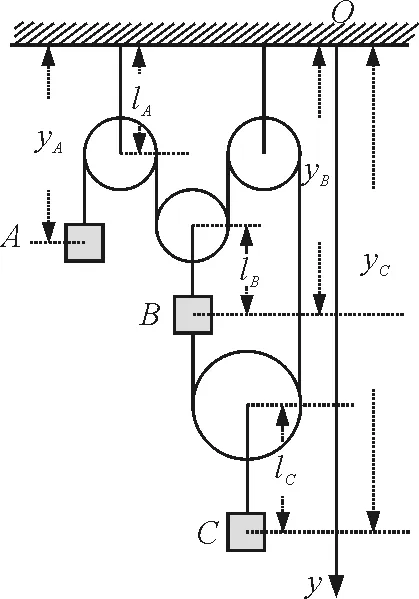
图1

分析与解：由于绕在滑轮组上面的绳的长度是固定的，不妨令绳总长度为l，同时整个系统仅涉及到竖直方向上的运动，建立如图1所示的竖直向下的坐标系Oy，则绳子的总长度可用A，B，C的位置及一些常量表示出来，从图1中不难看出

l=(yA-lA+πr)+2(yB-lB-lA)+πr+

(πr+yC-lA-lC+πR+yC-yB-lC)

式中yA，yB，yC分别表示物体A，B，C的位置，显然yA，yB，yC是随着时间变化的；r，R为小滑轮的半径和大滑轮的半径，lA，lB，lC为3个固定距离.因此有

l=(yA+yB+2yC)+(πR+3πr-4lA-

2lB-2lC)=(yA+yB+2yC)+c

其中

c=πR+3πr-4lA-2lB-2lC=const

(“const”表示常量)

在t时刻

l=l(t)=yA(t)+yB(t)+2yC(t)+c

(1)

在t+Δt(Δt→0)时刻

l=l(t+Δt)=

yA(t+Δt)+yB(t+Δt)+

2yC(t+Δt)+c

(2)

式(2)减去式(1)得

[yA(t+Δt)-yA(t)]+[yB(t+Δt)-yB(t)]+

2[yC(t+Δt)-yC(t)]=0

(3)

式(3)除以Δt后两边取极限得

根据

得

vA+vB+2vC=0

(4)

同理有

进一步得出

aA+aB+2aC=0

因此有

式中“-”表示物体C的加速度与物体A,B的加速度方向相反.

2.2 杆滑动问题

【例2】如图2所示，一杆长为l，搁在墙上，其下端端点A以恒定速度v向右滑动，当杆滑到与水平面成角α时，求杆上端端点B沿墙下滑的速度与加速度大小.

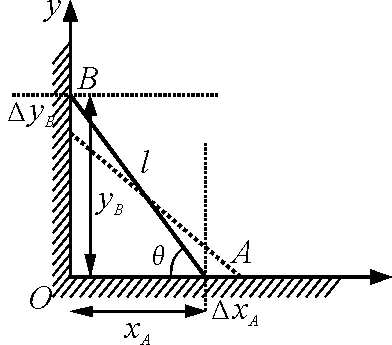
图2

分析与解：这是一道常见的物理题，只是关于杆上端端点B沿墙下滑的加速度大小的求法在习题中较为少见，若利用“极限”思想，学生只需要具备了初等数学的知识，就能顺利求出端点B沿墙下滑的加速度大小.由于杆的长度不变，同时整个系统的运动涉及到水平与竖直两个方向，因此可以建立如图2所示的二维直角坐标系xOy,在t时刻A,B的坐标分别为xA(t)=xA,yB(t)=yB，杆与水平面之间的夹角为θ，根据题意有

在t时刻

[xA(t)]2+[yB(t)]2=l2

(5)

在t+Δt(Δt→0)时刻

[xA(t+Δt)]2+[yB(t+Δt)]2=l2

(6)

此时，如图所示A和B的坐标分别变为xA+ΔxA和yB+ΔyB(其中ΔyB<0).

式(6)减去式(5)得

[xA(t+Δt)]2-[xA(t)]2+[yB(t+Δt)]2-

[yB(t)]2=0

(7)

式(7)除以Δt后两边取极限得

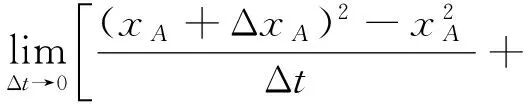
得

2xAvA+2yBvB=0

即

vB(t)=-vcotθ

当θ=α时

vB(t)=-vcotα

式中“-”表示物体B的速度沿着Oy轴负方向.

如图2所示,在t+Δt(Δt→0)时刻，θ变为θ+Δθ(其中Δθ<0)得

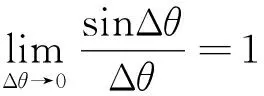
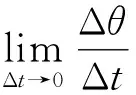
xA(t)=xA=lcosθ

xA(t+Δt)=lcos(θ+Δθ)

则有

由于

因此

则

当θ=α时

按照上面介绍的这种“极限”思想求解杆滑动问题中的一端点加速的思路也可以用在解决与此类似的物理问题.

3 结语

通过介绍物理学中的“极限”思想，进一步详细分析了“极限思想”求解物体的瞬时速度、瞬时加速度的方法与思路，学生只需要具备初等数学的知识，就能加深对物理量瞬时值的理解；理解了“极限”思想，对学生今后学习导数的概念也具有重要的启发意义.

1 全国中学生物理竞赛委员会.全国中学生物理竞赛专辑2014.北京：北京大学出版社,2014.6,12

2 人民教育出版社课程教材研究所,物理课程教材研究开发中心.普通高中课程标准实验教科书 物理·必修1(第3版).北京：人民教育出版社,2010.4,16

3 王溢然.中学物理思维方法丛书：数学物理法卷 .郑州：大象出版社,1999.9,177～178

4 张筑生.数学分析新讲(第一册).北京：北京大学出版社1990.1,97～98

2015-09-29)