蓝移啁啾与红移啁啾对非线性飞秒光孤子脉宽、脉冲抖动影响及抑制孤子自作用的研究

>> 1.珠海汉胜科技股份有限公司 2.湖南农业大学信息科学技术学院

曾辉1、2杨乔云1卓辉2

蓝移啁啾与红移啁啾对非线性飞秒光孤子脉宽、脉冲抖动影响及抑制孤子自作用的研究

>> 1.珠海汉胜科技股份有限公司 2.湖南农业大学信息科学技术学院

曾辉1、2杨乔云1卓辉2

一 引言

近年来，随着超高速光纤通信技术的不断发展，光纤传输中常常利用光孤子能有效抑制色散，能有效实现远距离传输和提高通信质量。但是，在飞秒量级脉冲中，光脉冲传输常常受到啁啾、群速度色散、三阶色散、五阶非线性作用、SPM调制作用以及自陡峭、自频移等影响导致光孤子传输使得脉冲形状发生周期或者非周期性畸变、脉冲频宽展宽或压缩、峰值呈不规则变化。因此，如何保持光孤子稳定传输成为光纤通信系统中最前沿研究热点。基于上述特点本文采用对称分布傅里叶算法对非线性修正项薛定谔方程数值模拟，着重对反常色散区和自相位调制作用下蓝移啁啾与红移啁啾对孤子脉冲传输演化图进行分析，得到当下正啁啾在一定数值范围内，随着数值增大，其红移现象愈加突出，不利于孤子间光脉冲传输。同理，在负啁啾作用下，当啁啾数值大小逐渐增大时，使得蓝移现象愈加显著但还是存在孤子弱干扰现象；进而提出采用多阶非线性增益控制的方法对光脉冲增益与放大，抑制光孤子自作用；这对改善通信过程中误码率问题提供一定理论依据。

二 物理计算模型及数值方法

超高速光纤通信系统中飞秒脉冲沿λ方向传输时满足的方程可从修正项非线性薛定谔方程出发表示如下：

式中A(λ,t)是脉冲包络复振幅，λ是传输距离，t是时间，n是高阶色散阶数，νGVD为群速度色散,是高阶非线性系数表达式，χ（3）指三阶电极化率，ko=noωo/c是载波频率在传输介质中波数，no是传输介质的折射率，βn是n阶色散系数, 同时有

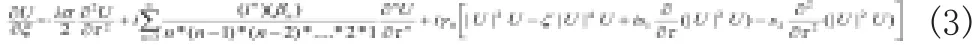
式中U(ξ,τ)为归一化脉冲包络复振幅，ξ,τ分别为归一化时间和距离，σ的取值范围在[-1,1]其中，光脉冲初始半宽度>>10fs, s=1/ωot，，S1，S2相对βn数值而言，可以忽略不计。其上述式中（3），选取λ=1.55μm，to=30fs，tR=3fs，β2=-20ps2/km，β3=-.1ps3/km，同时令：

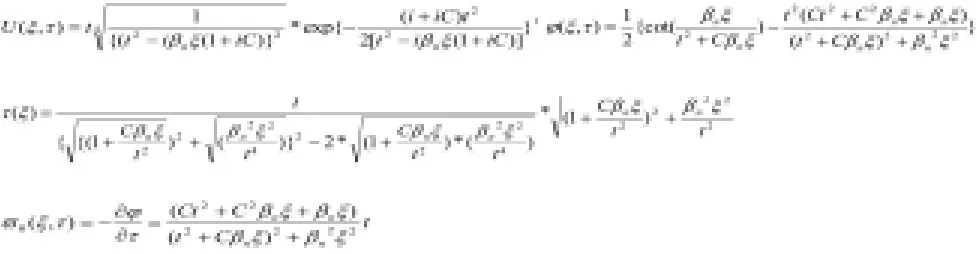
为方便数值计算，通过实践证明其分布傅立叶 算法为求解非线性薛定谔方程最佳有效方法，可将FFT算法原理分解为：

三 数值结果及分析

方程（3）为计算机编码模拟超高速光纤通信中超短脉冲孤子传输效应的数学建模公式，在此光脉冲传输过程常常需要考虑其GVD、SPM、初始啁啾、光纤损耗、二阶色散、三阶色散以及高阶非线性作用对孤子传输影响；在上述情况下选取孤子等距、振幅等同、初始啁啾不同；孤子脉冲公式可表示如下：

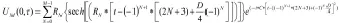
其中，M=2,3,4......2+(n-1)*,C为初始啁啾参量，设在正常色散区C=0,0.05,0.1,0.15,0.2;反常色散区C=-0.2,-0.15，-0.1；-0.05,0;RN=1,D=3.5（孤子间间距）,N=[0,+∞];通过MATLAB程序编码模拟在正啁啾与负啁啾情况下孤子间相互作用随初始啁啾变化产生如图1（a）上图,图2（c）上图,图3（e）上图所示，图像对比分析可知：当啁啾C=[0,0.2];ΔC=+0.05,其二孤子间峰值强度在C=[0,0.1]，Imax由1.8降为1.5；当啁啾递增至0.15时，其振幅峰值强度出现上升趋势I=1.58;随着啁啾数值不断增大至0.2时，此刻A强度再次减少；且在此过程中脉冲频谱增大，表现为延迟现象，脉宽逐渐向光脉冲波发射中心位置靠拢，呈压缩趋势，表现为脉宽减少。同时，通过分析图2（c）上图，三孤子间振幅强度在[1,1.6]波动；当初始啁啾由0→0.05时；其振幅最大峰值强度出现短暂递增，之后啁啾大于0.05时，其振幅均值从1.43→1.4与此同时，坐标x轴在[-15,10]之间不断向0靠近，使得脉宽不断压缩，其X轴大于15的位置，右频谱抖动加剧。同理，图3（e）上图，当啁啾不断递增至0.2时，振幅波动相对起始位置呈不规则变化、且振幅均值强度由1.5→1.45呈大致递减趋势，且通过发现在X轴左侧频谱抖动位置逐渐中心位置0移动，脉宽递减、脉冲延迟递增，左侧频谱抖动相对右侧抖动更频繁。故当啁啾在 时，其振幅均值强度随着啁啾数值增大而大致呈减少趋势，且孤子间作用不断增强，同时红移现象逐渐显著、脉宽减少。当啁啾C=[-0.2,0]时，同理，分析对比图1（a）中图, 图2（c）中图, 图3（e）中图当C小于O时，其X轴位置上远离发射波中心位置，其啁啾不断增大，脉冲抖动愈加减弱，且孤子外的频宽能量不断转移至就近孤子上。结合曲线图分析，故C=[-∞，0]时，其啁啾不断增大时，其脉宽展宽不断递增，呈舒展趋势，且孤子间作用表现减弱，脉冲延迟衰减、出现蓝移现象。为此，解决上述正啁啾中存在红移现象利于孤子传输和负啁啾中蓝移现象存在孤子弱干扰问题，进而在高阶非线性薛定谔方程基础上增加滤波装置对光脉冲补偿，达到增益目的、更稳定保持孤子间波形不变，故令;α=0.2，δ=0.03。通过增益之后，对比分析图1（b）上、下图, 图2（d）上、下图, 图3（f）上、下图发现不管是在正啁啾还是负啁啾情况下，通过非线性控制方法对孤子传输进行增益之后，其二孤子、三孤子、四孤子之间能维持较平稳传输且频谱变化呈基本稳定状态。且通过观察图1（b）中图, 图2（d）中图, 图3（f）中图发现增益后，其振幅曲线随正啁啾数值增大，其振幅均值依次呈振荡不规则变化，当C取[0,0.2]其大体呈AC=0.05>AC=0>AC=0.1>AC=0.2>AC=0.15；同理，在负啁啾作用下AC=0>AC=-0.05>AC=-0.2>AC=-0.15>AC=-0.1；因此，综上所述0＜C＜0.2时，随着啁啾不断递增，其孤子间红移现象愈加明显且脉冲延迟增加、脉宽减少；反之，-0.2＜C＜0时，啁啾越大，脉宽越大、频谱抖动衰减且蓝移现象逐渐显著。无论其啁啾如何变化在红移和蓝移现象中还是存在孤子间干扰；为此，进而采用多阶滤波装置对其光脉冲进行非线性放大增益，能较好使得入射孤子位置与出射位置保持一致，改善光脉冲过程中存在孤子互扰问题。

图1 正常色散区、反常色散区双孤子传输及抑制孤子干扰作用传输图

图2 正常色散区、反常色散区三孤子传输及抑制孤子干扰作用传输图

图3 正常色散区、反常色散区四孤子传输及抑制孤子干扰作用传输图

四 结论

本文首先对高阶修正项非线性薛定谔方程数值求解，然后采用分布傅立叶算法对NLSE方程线性算符与非线性算符分步运行；对其在一定数值范围内正负啁啾特性对孤子脉宽、脉冲抖动问题进行研究。同时，将非线性薛定谔方程在MATLAB科学计算软件数学建模分析，通过程序运行模拟发现：首先在正啁啾作用下，其脉冲脉宽随着啁啾增大呈正比变化，且红移现象愈加突出；脉冲延迟递增。反之，在负啁啾情况下，随着啁啾数值增大，利于蓝移现象出现，其脉冲抖动放缓，虽然能较好起到保持孤子平稳传输。但是，还会间断出现孤子互扰现象；为此，采用多阶非线性控制方法对其NLSE方程进行光脉冲放大与增益，能更有效改善正负啁啾对孤子传输互扰问题，使得在光脉冲在超远距离传输保持波形不失真，这将对减少超高速通信系统中信号衰减起到巨大作用。

国家自然科学基金项目(10674045)；国家科技部“国家星火计划”项目（2011GA770001）;国家科技部“十二五”重点课题（2011BAD21B03）；国家科技部“十二五”重点课题（2012BAD35B05）；湖南省教育厅科学研究重点项目（12A062）；湖南省科技计划重点项目（2013GK3106）湖南省教育厅学位基金项目( YB2010B024)