镁合金塑性变形过程中锯齿屈服现象的研究进展

李传强，许道奎，韩恩厚

(1.东北大学材料科学与工程学院，辽宁 沈阳 110819)(2.中国科学院金属研究所 中国科学院核用材料与安全评价重点实验室 辽宁 沈阳 110016)



特约专稿

镁合金塑性变形过程中锯齿屈服现象的研究进展

李传强1,2，许道奎2，韩恩厚2

(1.东北大学材料科学与工程学院，辽宁 沈阳 110819)(2.中国科学院金属研究所 中国科学院核用材料与安全评价重点实验室 辽宁 沈阳 110016)

在所有工程用金属结构材料中，镁合金的密度最低，具有较高的比强度和比刚度。然而，镁合金在一定的塑性变形条件下会出现明显的“塑性不稳定”现象，也被称作锯齿屈服(流变)现象或Portevin-Le Chatelier(PLC)效应，主要表现为应力-应变曲线上的锯齿状波动。近年来，关于镁合金PLC效应的研究报道逐年增加。本文将重点介绍镁合金中存在塑性不稳定现象相关的研究进展，叙述并归纳镁合金PLC效应发生的条件、锯齿屈服的特征、合金元素对锯齿屈服现象的影响及对应的理论机制等。最后，指出目前研究中尚存在的问题，提出将来的研究重点和发展方向。

镁合金；Portevin-Le Chatelier效应；锯齿流变；变形机制；微观组织

1 前 言

对于晶体材料而言，塑性变形是一个复杂非均匀的过程，且伴随着一系列位错运动的无标量和间歇性的剪切崩塌行为，其中应力突变的产生主要由剪切带的协同开动和剪切崩塌所引起的[1]。在塑性变形初期，合金的应力应变曲线上会出现一个应力平台[2]。另外，在一定塑性变形条件(温度和应变速率)下，Mg、Al和Ni基合金均会出现一种连续的塑性失稳现象，即整个应力-应变曲线均呈锯齿状波动，且锯齿波的类型会随着变形条件的变化而变化[3-10]。1923年，Portevin和Le Chatelier首次对这种连续的锯齿屈服现象进行了系统的研究，并将该屈服现象定义为Portevin-Le Chatelier(PLC)效应[11]。1984年，Rodriguez等归纳了导致PLC效应可能的7个主要原因[12]：①位错密度的增加；②可动位错的动态应变时效；③可动位错有序向无序的转变，渐变或调整；④变形孪晶的产生；⑤位错切割第二相粒子；⑥材料温度的突变或温度的不均匀传递；⑦应力或应变诱导相变。

在众多金属材料中，镁是地壳中储量较多的金属元素之一(2.l wt%)，仅次于铝和铁，居第三位，且镁的密度为铝的2/3，是最轻的结构用金属结构材料，其比强度高、比刚度高、具有优良的导热和导电性能，具有广泛的应用前景[13-15]。然而，直到上世纪50～60年代，研究人员才发现镁合金中也存在PLC效应[16,17]，并揭示出Mg-0.5wt%Th合金中存在的PLC现象只在较高的变形温度条件下出现，但在室温条件下却会消失。可以看出，镁合金中存在的锯齿屈服现象可能与原子气团对可动位错的钉扎作用有关。由于室温下镁合金中的非基面滑移需要的临界剪切应力远高于基面滑移所需的临界剪切应力，所以溶质原子与可动位错之间的交互作用很弱，不足以引起应力的锯齿波动，最终导致锯齿屈服现象的消失。在对含氮量仅为0.0008～0.0048 wt%镁单晶材料的研究中[18]，Geiselman等发现只有当材料经高温固溶和200 ℃时效处理后才会出现锯齿屈服现象，且所需的变形温度要在200 ℃以上，这主要归因于氮原子形成的Cottrell气团对可动位错的钉扎作用。同时，Chiao和Kossn等发现镁单晶材料在高温和室温下均能表现出锯齿屈服现象[19,20]，且应力下降的幅度随变形温度的降低而变小，表明当进入塑性变形阶段时样品中的位错密度会出现陡然增加。与此类似，Huseby等也将Mg-25vol%B复合材料在拉伸过程中出现的锯齿屈服现象归因于位错密度的陡然增加[21]。近年来，Koike等报道了经等径道挤压(ECAE)制备的AZ31镁合金样品在室温拉伸应力-应变曲线上会出现应力平台，并将该现象归因于非基面滑移的开动与晶界的协调作用[22]。另外，Agnew和Mora等报道孪晶的大量形成也会促使镁合金在塑性变形时应力的下降[23,24]。可以看出，镁合金的锯齿屈服现象可能与位错滑移和孪晶的启动有关。

总体而言，关于镁合金中PLC效应的研究起步较晚，远不如铝合金中的那么广泛和深入，且学者们的观点缺乏统一。本文将对迄今有关镁合金PLC效应的特征及发生的条件、锯齿屈服的特征和合金元素对锯齿屈服现象的影响及可能的理论机制方面的报道进行归纳和总结。最后，指出目前对镁合金中PLC效应研究中尚存在的问题，并对将来的研究重点和方向进行展望。

2 锯齿屈服的特征

在对AZ81镁合金力学行为的研究中，陈立佳等提出镁合金锯齿屈服现象主要具有3个特征[25]：①出现负的应变速率敏感性系数；②应力应变曲线在一临界应变点之后出现锯齿型波动；③强度随变形温度的升高无明显变化或出现应力平台。然而，Stanford等在研究和对比Mg-Gd和Mg-Al合金应变速率敏感性时[26]，发现两种合金均发生锯齿流变现象，且它们的延伸率在锯齿流变的温度变化区间内基本不变，但在相同流变条件下Mg-Gd合金的塑性较低，表明Mg-Gd合金的应变速率敏感性系数较负。因此，负的应变速率敏感性系数并不是镁合金发生PLC效应的必要条件，但可以影响合金的塑性。Wang等在研究Mg-Li-Al合金的塑性不稳定性时[27-29]，发现随着应变速率的升高Mg-4%Li-1%Al(LA41)合金的锯齿波动幅值会有所减小，但其应变速率敏感性系数会随着流变过程发生正负波动。其中，镁合金中的正应变速率敏感性系数主要归因于[27]：应变速率越高，镁合金中启动的孪晶数量就越多，位错与孪晶的交互作用就越强，强度也就会越高。另外，基面的临界剪切应力随着应变速率的提高也会略有增加。由于这些微观强化机制抵消了合金动态应变时效的软化效应，最终使合金表现出正的应变速率敏感性。对于镁合金中负的应变速率敏感系数，主要解释如下[29]：在一定的温度和应变速率范围内，溶质原子对高速率运动位错的拖曳作用力小于与低速率运动位错的拖曳作用力，宏观上此作用力的差别便体现为在不同应变速率下流变应力的差异，即在达到同一应变情况下，高应变速率拉伸所需的应力小，而低应变速率拉伸所需的应力大，致使合金的应变速率敏感系数为负。Cai等发现含18R和14H长周期相的两种Mg-10%Dy-1%Zn合金在发生锯齿流变的温度区间内的应变速率敏感性系数为负，而在其它温度区间为正[30]。可见，应变速率敏感性系数的正负与变形条件和合金的化学成分等存在一定的内在联系。

关于镁合金随变形温度增加出现应力平台的特殊现象，已有很多的相关报道。Zhu等发现Mg-Y-Nd(WE54)合金在中间变形温度区间内会发生PLC效应并出现应力平台[31]，且延伸率随温度升高而呈现出正常的递增趋势，如图1所示。对于其它镁合金如AZ81合金[25]，Mg-Gd-Zn合金[32]，Mg-Nd-Zn合金[33]等，研究人员也发现了类似现象。可见，这种应力平台现象的出现除了与位错和溶质原子之间的交互作用有关。当然，孪晶的作用也不容忽视。另外，镁合金在高温变形过程中可以发生动态回复，会对合金的强度和塑性产生一定的影响。Stanford等研究发现对于含稀土镁合金而言，变形孪晶的启动(低温下)和回复及动态再结晶(高温下)是影响合金塑性的主要因素[26,34]。在200 ℃温度条件下，纯镁、Mg-Al与Mg-Gd合金的变形机制有所不同[26]，其中纯镁在该温度下发生了再结晶，Mg-Gd合金产生了更多的变形孪晶，而Mg-Al合金介于两者之间。目前，国内外学者对存在的应力平台缺乏系统的研究和统一的见解。

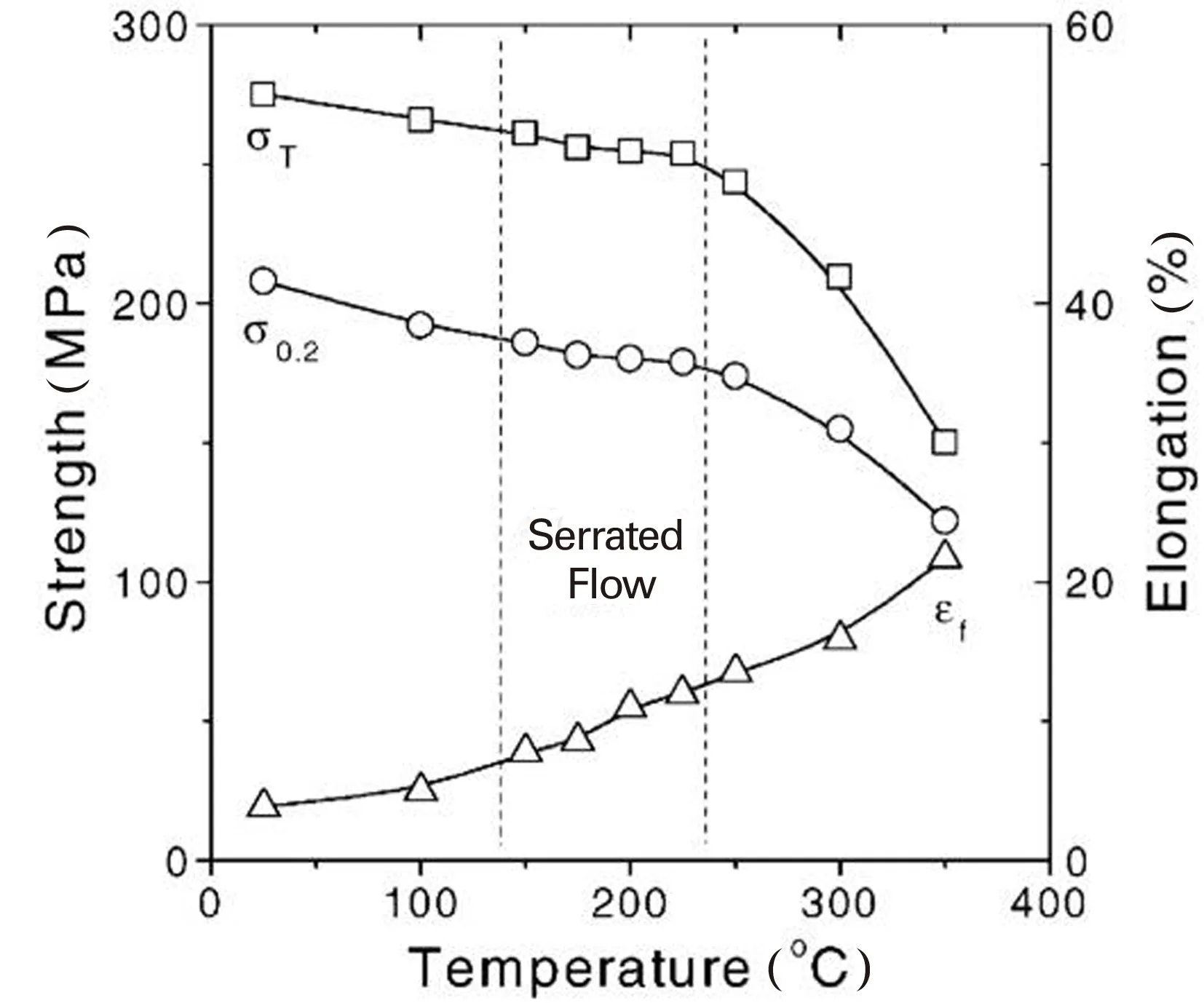
图1 WE54合金在应变速率为5.6×10-4 s-1时的屈服强度σ0.2、抗拉强度σT、延伸率εf与温度的关系[31]Fig.1 Temperature dependence of 0.2% yield strength σ0.2,ultimate tensile strength σT,and elongation to fracture εf.The strain rate employed is 5.6×10-4 s-1[31]

通常，镁合金中锯齿屈服现象的发生往往需要达到一个临界应变值εc，主要的解释如下[25]：在固溶体合金中，溶质原子只能通过空位来进行有效的扩散，而这种原子扩散所需的空位只能通过一定量的塑性变形来获得。因此，要出现锯齿流变现象，就需要达到一个临界应变量，且临界应变量与应变速率和变形温度有着密切的关系。在对Mg-0.8%Ca合金力学行为的研究中，Peng等发现合金在室温下出现PLC效应所需的临界应变会随着应变速率的增高而增加[35]。Sha等发现Mg-3.5%Li合金在0.5 mm/min的拉伸速率下出现PLC效应所需的临界应变值为6.7%，而在5 mm/min的拉伸速率下对应的临界应变为9.3%[36]。采用声发射技术，Trojanova等研究了AZ91镁合金锯齿流变的临界应变[37]，揭示出林位错的产生会引起变形初期局部小变形带的形成。随着塑性变形的进行，这些小的变形带会逐渐增多并叠加，从而增加变形带所引起的局部应变量，直至出现宏观的锯齿屈服现象。利用公式Δεvb≥i[37]，可以清楚表达这一过程。式中，Δε是变形带引起的局部应变量，vb是变形带的移动速率，i是外加试样的宏观应变速率。当应变量较低时，异种位错形成的林位错密度较低，变形带所产生的应变量较小，不能满足上述公式，位错将以平滑方式扩展运动。随着应变量的增加，林位错的密度增大，临近的小变形带将合并而增加单个变形带所引起的应变量，直至满足公式。此时，试样将表现出明显的宏观锯齿效应。

在镁合金锯齿屈服所需的临界应变和温度的关系研究中，Zhu等发现WE54合金在温度为150～225 ℃和应变速率为5.6×10-4s-1的条件下具有PLC效应，且对应的临界应变量会随着温度升高而减小[31]。采用数值模拟计算方法，Cai等证明了镁合金中PLC效应发生时对应临界应变量随着温度的升高而减小的变化关系[38]。另外，Wang等发现Mg-2.7%Nd-0.6%Zn-0.5%Zr合金发生PLC效应时对应的临界应变εc与温度并不是呈简单的线性关系，而是随着温度的升高先降低后升高[39]。可见，PLC效应对应的临界应变量是由多种因素决定的。基于此，Wang提出了新的概念，即溶质原子钉扎位错的临界应变εcp(Critical Strain for Pinning)和位错脱钉的临界应力σcu(Critical Stress for Unpinning)[39]，并用示意图清楚表达了溶质原子钉扎位错时对应的临界应变εcp、位错脱钉时对应的临界应力σcu、临界应变εc、锯齿波类型和变形温度等之间的关系，如图2所示。其中，εcp值随着温度的升高而降低，σcu值随着温度的升高而增加。当应力(σ)达到位错脱钉所需的临界应力σcu，而应变ε小于位错被钉扎所需的临界应变εcp时，即σ>σcu和ε<εcp，如区域Ⅰ，锯齿流变将不能发生，主要因为此时溶质原子对位错的钉扎很弱。当应变(ε)达到位错被钉扎所需的临界应变εcp，而应力σ小于位错脱钉所需的临界应力σcu时，即σ<σcu和ε>εcp，如区域Ⅳ，锯齿流变也不能发生，主要因为被钉扎的位错很难脱钉。当应变ε达到位错被钉扎所需的临界应变εcp，应力σ也达到位错脱钉所需的临界应力σcu时，即σ>σcu和ε>εcp，如区域Ⅱ和Ⅲ，锯齿流变才能发生。

图2 溶质原子钉扎位错的临界应变εcp，位错脱钉的临界应力σcu，临界应变εc，锯齿波类型和变形温度的关系示意图[39]Fig.2 Diagram of the relationships among critical strain εc,critical strain for pinning εcp,critical stress for unpinning σcu,serration types and temperature [39]

3 锯齿屈服的条件

镁合金锯齿屈服的发生除了要达到一临界应变外，还需满足一定的外部条件如变形温度和加载速率等。在研究铸态Mg-2.7%Nd-0.6%Zn-0.5%Zr(NZ31)镁合金高温力学行为的过程中[33]，Wu等发现合金在200 ℃和250 ℃时表现出明显的锯齿屈服现象，且延伸率随温度的升高呈现出先升后降的反常现象，这主要归因于高温变形时锯齿屈服更易引起应力局部集中并导致塑性的降低。当温度低于200 ℃时，合金的应力应变曲线上并没有锯齿波动现象，这主要因为低温下位错运动能力较低，且时效析出相可以进一步抑制位错的运动。相反，高温条件下位错运动能力很强，位错可以切过第二相，从而导致了PLC效应。轧制态Mg-2.74%Gd-1.06%Zn(GZ31)合金在150～250 ℃中间温度和应变速率为1×10-4～ 1×10-2s-1条件下塑性变形时，将会出现锯齿屈服现象，但塑性也会有所损失[32]。Cai等发现含长周期相的Mg-10%Dy-1%Zn合金也只在应变速率为5×10-2s-1和变形温度为150～250 ℃的条件下，锯齿屈服现象才会发生[30]。对于Mg-Y-Nd合金而言，其PLC效应出现需要的应变速率为5.6×10-4s-1，所需的变形温度为150～225 ℃[31]。在对Mg-4.9%Y-4.2%Nd-0.56%Zr合金的平面应变压缩和单轴压缩行为的研究中，Azzeddine等发现合金在两种塑性变形条件下发生PLC效应所需的温度为300 ℃和400 ℃，所需的应变速率为1×10-4s-1[40]。Wang等[41]发现T4和T6态Mg-4%Zn-3%RE(ZE43)合金仅在120～240 ℃温度区间存在锯齿屈服现象，而其它温度条件下不会出现。当应变速率为5×10-5～1×10-4s-1时，热挤压AZ81镁合金发生PLC效应的温度范围为125～200 ℃，而当应变速率为5×10-4s-1时，合金发生PLC效应的温度范围为150～200 ℃[25]。然而，在对Mg-3%Al-1%Zn-0.1%RE合金PLC效应的研究中[42]，Qiu等发现当应变速率为1×10-4s-1时，合金可在393～453 K的温度区间表现出PLC效应，而当应变速率为5×10-4～1 s-1时，合金仅在453K温度下出现PLC效应。Sha等对Mg-3.5%Li合金的力学行为进行了研究[36]，发现合金在0.5 mm/min和5 mm/min拉伸速率下具有明显的PLC效应，但在0.05 mm/min和50 mm/min拉伸速率下拉伸曲线是光滑的，无PLC效应。Hidalgo等对Mg-1%Mn-1%Nd(MN11)合金在中间变形温度(150～300 ℃)存在明显的锯齿效应给予了解释[43]：HCP结构的镁合金在中间温度变形，位错的启动会引起应力与温度反常的关系，并计算出在1×10-3s-1的应变速率下镁合金中的基面、柱面和锥面滑移及孪晶启动所需的临界剪切应力与温度的关系，如图3所示。可见，随着温度的升高，非基面位错密度将会增大。因此，MN11合金的PLC效应与非基面位错的启动关系很大。

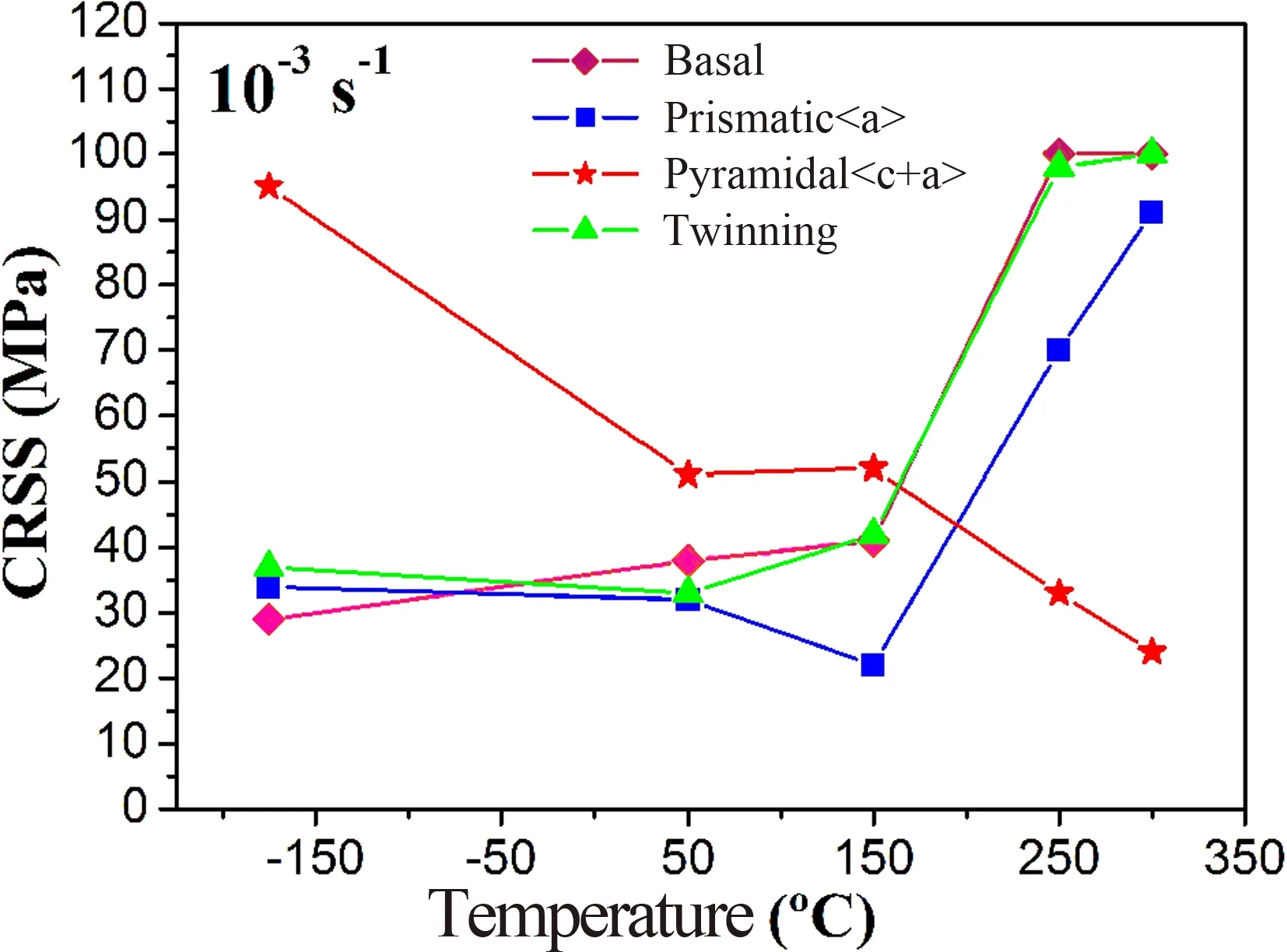
图3 应变速率为1×10-3 s-1时，不同变形机制模型的临界剪切应力(CRSS)与温度的关系[43]Fig.3 Critical resolved shear stress (CRSS)values for the different deformation modes at 1×10-3 s-1 as a function of temperature [43]

综上所述，镁合金往往倾向于在中间变形温度区间内发生PLC效应。其原因可做如下解释：当温度较低时，溶质原子扩散能力较差，在位错被障碍物阻碍过程中的停留时间内，不能形成气团对位错进行有效钉扎。随着变形量的增加或应变速率的提高，位错将可以进行平滑地扩展运动，宏观上应力将不会出现波动。当在中间变形温度区间内塑性变形时，溶质原子扩散能力增强，可以对可动位错实施有效钉扎。随着应变速率的升高，位错将会脱钉，导致应力的下降，继而位错可再被钉扎和脱钉。如此往复，宏观上将表现出锯齿屈服现象。当在高温条件下变形时，溶质原子气团和位错将一起运动，位错不容易发生脱钉，应力不会发生突变，从而抑制了PLC效应。

另外，早期关于镁合金中存在PLC效应的研究主要侧重于应变速率往往小于1×103s-1的加载条件。然而，在一些高速运动的物体发生碰撞时，瞬间应变速率可超过1×103s-1，材料的变形行为将会发生改变。Feng等在对AZ31B镁合金的高应变速率拉伸行为的研究中[44]，发现当应变速率大于1397 s-1时，合金的拉伸曲线表现出明显的锯齿波动现象，且强度和延伸率均明显高于低应变速率条件下的，如图4所示。同样，Hidalgo等发现MN11合金在快速应变速率为103s-1时的锯齿流变效应也很明显[43]。Dudamell等揭示出MN11合金在高应变速率条件下基面滑移所需的剪切应力会减小，且孪晶对PLC效应的作用会减弱[45]。迄今，关于镁合金在高应变速率条件下的锯齿屈服现象的相关研究报道较少，相关机理性的解释还很缺乏，与慢应变速率条件下发生锯齿屈服现象的差别尚不清楚。

图4 室温下，AZ31B合金的动态和准静态拉伸实验的工程应力应变曲线[44]Fig.4 The engineering stress-strain curves of AZ31B alloys under dynamic and quasi-static tensile tests at room temperature [44]

除应变速率和变形温度外，镁合金的晶粒尺寸和合金元素与PLC效应的出现也存在着一定的关系，Rodriguze等[12]发现合金的晶粒尺寸越小，锯齿流变越易发生，原因为晶粒越小晶界就越多，可为溶质原子在晶界的偏聚提供更多位置，最终增强了位错与溶质原子之间的交互作用。

4 合金元素对镁合金PLC效应的影响

合金元素加入到镁基体中，将形成不同浓度的固溶体，势必会影响到镁合金的PLC效应。Stanford等研究并对比了纯镁、Mg-1.4%Gd和Mg-1%Al三种材料在200 ℃的变形温度条件下的锯齿流变行为[26]。采用三维原子探针技术，检测了溶质原子的分布，发现溶质原子Gd主要呈线性集中分布(如L1和L2)或呈团簇集中分布(如C1和C2)，如图5所示。对不同区域的溶质原子进行定量分析，表明Gd原子在位错处的浓度是基体中的2倍以上，而其它元素(如Al和Mn)却没有明显的聚集现象。

图5 200 ℃温度下Mg-1.4Gd合金应变速率突变后Gd元素的三维分布图：(a)所有Gd原子的分布图，(b)～(c)是高浓度Gd原子的分布位置[26]Fig.5 APT reconstruction of the Mg-1.4Gd alloy after strain rate jump tests at 200 ℃:(a)image showing all detected Gd atoms,(b)～(c)images showing the high concentration locations of Gd atoms [26]

在研究不同Zn和Al元素含量的Mg-Zn、Mg-Al和Mg-Al-Zn等五种镁合金的力学行为过程中，Corby等发现仅有AZ91镁合金存在锯齿屈服现象[46]。可见，Al和Zn的共同作用与AZ91合金中存在的PLC效应密切相关。Lukác等对此现象进行了两种机制性解释[47,48]：一是扩散机制：即随着Zn含量的增加，柱面滑移的临界剪切应力将明显减小。在塑性变形过程中，基面位错向柱面双交滑移而形成的林位错密度会有所增加，致使Al原子可通过管扩散机制向位错附近扩散，从而达到钉扎位错的效果。由于Zn原子的半径比Al大，Zn扩散能力相对较差。因此，Al产生动态应变时效的程度比Zn大。二是非扩散机制：即镁合金在变形过程中基面滑移最先启动，从而形成基面位错团，导致应力的局部集中，继而通过二次滑移(柱面)释放应力而形成林位错。随着塑性变形的进行，林位错密度不断增加，穿过此位错林就需更多位错的塞积。同时，位错林也随着变形的增大而增多，导致位错源可以释放出更多的位错。若由此引起的微观应变速率大于外加的宏观应变速率，则应力将会出现陡然降低现象。因此，Zn的作用是促进柱面滑移，形成更多的林位错，而Al原子可通过扩散机制对位错进行钉扎，最终致使AZ91合金的锯齿屈服现象。

在对溶质原子浓度与PLC效应的关系性研究中，Gao等揭示出不同Y含量(0.2,0.34,0.86,1.32和1.88 at%)对二元铸态单相Mg-Y合金PLC效应的影响规律[49]。在250 ℃温度条件下，几种Mg-Y合金均表现出明显的PLC效应，且随着Y含量的增多，锯齿效应越加明显，如图6a所示。Azzeddine等发现在同样的压缩条件下，WE54合金的PLC效应明显强于AZ31合金[40]，如图6b所示。可能的解释是：镁基体中Y、Nd溶质原子与位错的交互作用要强于Al和Zn原子。Stanford等研究发现Al的原子半径比Mg小20%，Gd的原子半径比Mg大13%，但Mg-Gd合金的锯齿效应却更加明显[26]。综上所述，镁合金中存在的PLC效应不是决定于溶质原子/溶剂原子半径差的绝对值，而是与溶质原子的扩散能力及溶质原子的浓度更为相关。

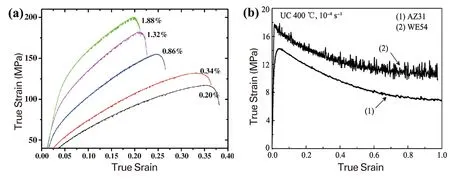
图6 (a)当温度为250 ℃，应变速率为10-3 s-1时不同Y含量的Mg-Y合金的应力应变曲线[49]和(b)当温度为400 ℃，应变速率为10-4 s-1时WE54 和AZ31合金的流变屈服曲线[40]Fig.6 (a)Segments of flow curves obtained at 250 ℃ and a strain rate of 10-3 s-1 for the Mg-Y alloys,the labels in image (a)indicate the yttrium concentration in at% [49]and (b)stress-strain curves of WE54 and AZ31 alloys at 400 ℃ and a strain rate of 10-4 s-1 [40]

锂是最轻的金属元素，当加入到镁基体中，会形成一种最轻的金属材料即Mg-Li合金[10,50-54]。由于Li原子的半径很小，扩散能力很强，且Li的加入可降低镁合金的c/a轴比，有效降低非基面滑移的临界剪切应力。因此，Mg-Li合金PLC效应将会更易发生[10]。Mg-Li合金所具有的独特特点是：随着Li含量的增多，合金的结构会发生转变[55,56]，即HCP结构(Li：<5.5 wt%)→(HCP+BCC)结构(Li：5.5～11.2 wt%)→ BCC结构(Li：>11.2 wt%)，这种相结构的转变对镁锂合金PLC效应的影响尚不清楚。通常，Mg-Li合金发生PLC效应的温度区间明显比其它系列镁合金的低，甚至在低于室温条件下也能发生。可能的解释是：Li原子的半径很小，所需的扩散能比其它溶质原子要低，可在较低温度下发生扩散并产生动态应变时效。对固溶态Mg-14.3%Li-0.8%Zn合金的低温力学性能的研究中，Wu等发现合金在-25和-50 ℃温度条件下具有最明显的PLC效应，且锯齿的幅值最大[57]。Li等发现在高于100 ℃的变形条件下，挤压态Mg-4%Li-6%Zn-1.2%Y合金的宏观应力应变曲线上将观察不到明显的PLC效应[10]。另外，李廷取等发现在LAZ532-2RE合金的拉伸曲线中存在两种塑性失稳现象[58,59]。其中，第一种是小锯齿形波动的失稳现象，第二种是大锯齿形波动的严重失稳现象。对于小锯齿波的出现，可能是由固溶原子与位错相互作用引起的，即“动态应变时效”机制。对于大的锯齿波的出现，可能是由切变孪晶诱发的，即“孪晶诱导稳态塑性失稳”机制。在研究Mg-Li-Al合金的PLC效应过程中，Wang等发现没有锯齿效应的LA11合金的声发射信号要弱于具有PLC效应的LA41合金[60]，其原因为LA41合金的轴比c/a较低，柱面滑移启动比LA11的容易，较多的滑移系的启动引起了更强烈的声发射信号。在室温变形条件下，具有较低轴比c/a的Mg-Li合金中基面位错向柱面的双交滑移而导致林位错的形成，致使Li和Al等溶质原子可以管道机制进行扩散。另外，双相结构的镁锂合金往往没有PLC效应，这与两相的协调变形有密切的关系。例如，Xu等[8-10,50,53]研究发现在同样的变形条件下，单相Mg-4%Li-(6%Zn-1.2%Y)合金表现出明显的PLC效应，而Mg-6%Li-(6%Zn-1.2%Y)合金却没有PLC效应。

5 镁合金锯齿屈服现象的理论机制

5.1 动态应变时效

通常，应变时效分为静态和动态应变时效，前者是合金材料在发生塑性变形时或产生塑性变形后所发生的时效过程；后者是变形和时效同时发生的过程，即溶质原子与位错的交互作用[61]。在解释PLC效应的理论机制中，动态应变时效是最先被建立的，也是被学者们广泛接受的。塑性变形时，位错被溶质原子气团钉扎时，其密度将会有所增加。当位错挣脱溶质原子的束缚时(往往这是一个突变过程)，应力将迅速减小。若溶质原子扩散速率与位错的移动速度相当，则溶质原子可再次对位错实施钉扎，导致应力再次增加，继而位错再脱钉，应力再减小。如此反复，应力应变曲线就呈锯齿状变化[62]。然而，基于目前的研究技术，很难直接观察到动态应变时效现象，而学者们往往利用静态应变时效的试验间接证明动态应变时效的存在。在应变速率为0.05 s-1和变形温度为200 ℃的静态应变时效条件下，Cai等[30]发现含18R长周期相的Mg-10%Dy-1%Zn合金在时效1～10 min后出现了明显的屈服点，即应力值陡然升高，如图7所示。由此说明，静态应变时效过程中溶质原子会向位错周围聚集，这也间接说明含18R长周期相合金的锯齿流变现象与动态应变时效密切相关。Zhu[31]和Wu[32]等对Mg-Y-Nd和Mg-Gd-Zn合金中存在PLC效应的解释也采用了类似的方法。

图7 当温度为473 K (200 ℃)，应变速率为0.05 s-1时，含18R-LPSO相的Mg-10%Dy-1%Zn合金静态应变时效后的真应力应变曲线[30]Fig.7 True stress-strain curves showing the effect of statically aged Mg-10%Dy-1%Zn alloy containing 18R-LPSO at 473 K (200 ℃)and a strain rate of 0.05 s-1 [30]

5.2 位错切割第二相

Wang等认为因位错切割第二相颗粒所导致的PLC效应最终也归结为动态应变时效的作用[41]。由于位错切割第二相会引起相的快速溶解，并使溶质原子在位错线周围重新分配，从而导致动态应变时效的发生，这个过程也被称作二次动态应变时效。另外，镁合金中第二相的体积分数、分布、尺寸及其与基体的取向关系等都与PLC效应有一定关系[41]。通过DMD(Disintegrated Melt Deposition)方法，Hassan等制备出Y2O3纳米颗粒强化镁基复合材料[63]。在室温条件下，该镁基复合材料的拉伸曲线表现出明显的PLC效应。然而，经粉末冶金法制备出类似镁基复合材料的锯齿效应却不明显。Qiu等将Mg-3%Al-1%Zn-0.1%RE合金在不同温度和应变速率下表现出的PLC效应也归因于位错切割第二相粒子[42]。Wu等[32]发现轧制态GZ31合金在200 ℃拉伸时表现出PLC效应，但经480 ℃保温1 h后，合金中第二相被固溶，PLC效应也相应消失，可能原因是基体中溶质原子过多，位错不能摆脱气团的束缚，动态应变时效也很难发生。随后，再在300或350 ℃温度下进行时效处理，第二相将大量析出，PLC效应又会重新出现。这一结果充分说明位错切割第二相是GZ31合金中存在PLC效应的主要原因。通过对变形后的表面进行微观观察，Wu等获得到了位错切割第二相粒子的直接证据，如图8所示。

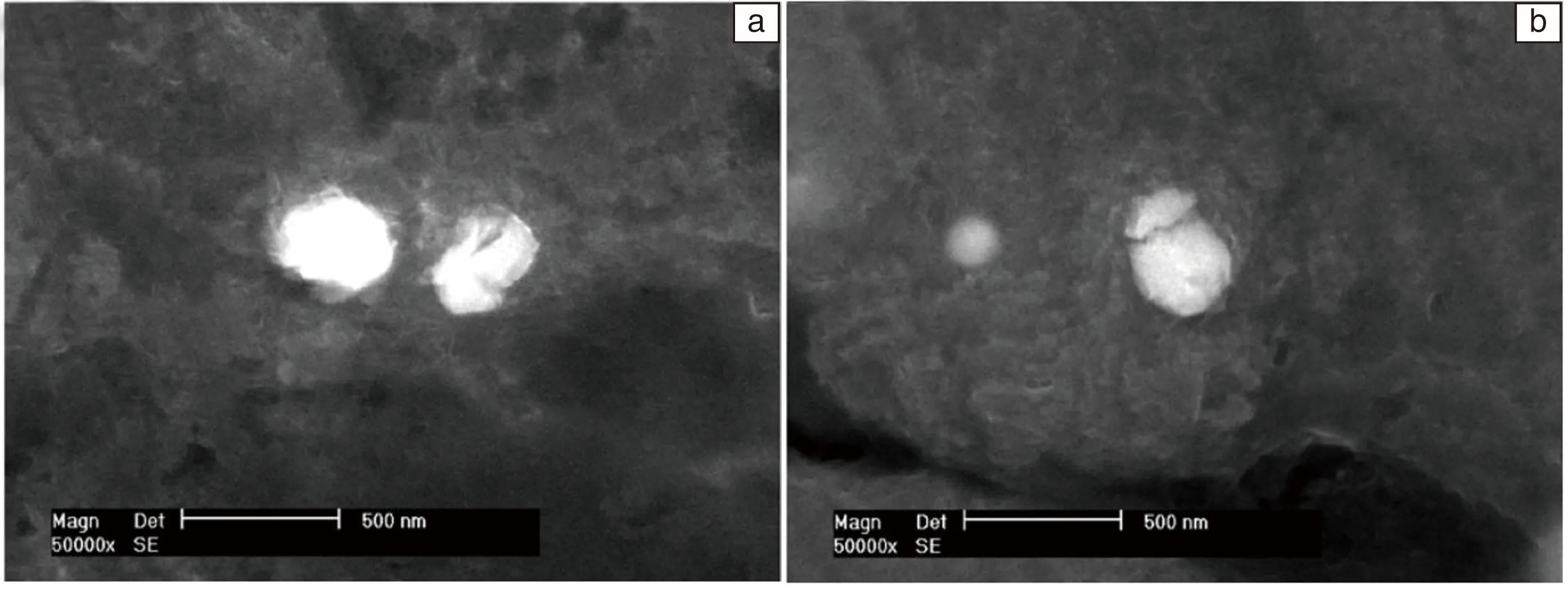
图8 GZ31合金的扫描电镜照片：(a)和(b)分别为200 ℃和1×10-3 s-1的拉伸应变速率条件下应变量为0.1时第二相粒子的前后变化情况[32]Fig.8 SEM micrographs to the secondary phase particles in GZ31 alloy:(a)before and (b)after being tensile deformed to ε=0.1 at 200 ℃and a strain rate of 1×10-3 s-1[32]

5.3 孪晶的作用

由于密排六方结构的镁合金所具有的独立滑移系较少，孪晶是其主要的变形机制之一。近年来，学者们也逐步重视孪晶与镁合金PLC效应的关系性研究。Dudamell等[45]发现MN11合金在200 ℃变形时，PLC效应最明显，同时变形孪晶也最多。当PLC效应减弱时，合金中的孪晶数量也减少。李廷取等[58,59]发现LAZ532-2RE合金应力应变曲线的中期，锯齿波幅值较大，在初期和末期的锯齿波幅值较小，并对3个试样分别在严重锯齿屈服前、严重锯齿屈服时、严重锯齿屈服后停载并观察其微观组织的变化，如图9所示。可以看出，在严重锯齿屈服前几乎没有孪晶，在严重锯齿屈服时存在少量的孪晶，在严重锯齿屈服后观察到了大量的孪晶。因此，大锯齿波的出现主要归因于孪晶的启动和增加。Wang等[27]发现LA41合金经过退火处理，基体中存在较多的退火孪晶，但该状态合金却无PLC效应，这主要是因为孪晶可以阻碍位错的运动，致使动态应变时效和位错切割第二相都不能发生。因此，合金中预先存在的孪晶可以抑制PLC效应。王聪等[29]对变形过程中形成的孪晶与LA41合金PLC效应的关系进行了研究，发现LA41合金在应变速率为6.66×10-4s-1，应变量分别为4.5%，10%和17%时，变形孪晶并未随应变量的增加而增多，说明变形孪晶并不是引起LA41合金塑性不稳定的直接起因。Zhu等[31]发现Mg-Y-Nd合金在150～225 ℃温度条件下出现PLC效应，但从变形3%的微观组织中发现，在没有出现PLC效应的室温条件和表现明显PLC效应的200 ℃温度条件下合金中均存在滑移带和孪晶，说明孪晶和PLC效应没有必然关系。综上所述，早期报道的关于孪晶与镁合金PLC效应的关系存在一定矛盾性，关于其中的机理性解释至今尚未有深入的报道。

图9 (a)LAZ532-2RE合金以应变速率1×10-3 s-1进行的分段拉伸曲线，(b)严重锯齿屈服前对应的微观组织，(c)严重锯齿屈服时对应的微观组织，(d)严重锯齿屈服后对应的微观组织[58]Fig.9 (a)Step-tensile curves of LAZ532-2RE alloy tested at a strain rate of 1×10-3 s-1,(b)initial microstructure before the occurrence of serrated flow PLC effect,(c)microstructure corresponding to the occurred severe PLC effect,(d)microstructure after severe PLC effect [59]

5.4 其它

镁合金PLC效应的发生需要满足一定的温度条件，而在高温变形条件下位错可挣脱溶质原子的束缚，同时动态再结晶也易于发生。因此，Azzeddine等将WE54镁合金在400 ℃的高温变形下表现的PLC效应归因于不连续动态再结晶[40]。在对含14H长周期相Mg-10%Dy-1%Zn合金中PLC效应的研究中，Cai等发现在静态应变时效过程中合金的屈服点无明显突变现象[30]，进一步微观分析表明合金的锯齿屈服现象主要与{10-12}晶面处形成的微裂纹有关，如图10所示。

图10 含14H-LPSO相Mg-10%Dy-1%Zn合金的透射电镜照片，表明在锯齿屈服过程中形成了微裂纹并与14H-LPSO相呈一定角度[30]Fig.10 TEM micrograph of Mg-10%Dy-1%Zn alloy containing 14H-LPSO phases,indicating some micro-cracks and 14H-LPSO phases intersected with each other during the serrated flow[30]

6 结 语

轻质镁基合金材料的PLC效应无论在时域还是空域上都是一个复杂的过程，也是材料科学前沿领域中的热门研究课题。在塑性变形时因PLC现象所产生的变形带会造成镁合金板面上的带状迹痕，影响板材的外观，限制了其在功能和结构件中的应用。目前，虽然学者们对镁合金PLC效应的研究逐渐增多，但仍存在一些至今尚未阐明的问题，如PLC效应宏观剪切带的形成、演化与传播机理，变形带的宽度与试件厚度的关系，孪晶与PLC效应的关系等。鉴于此，对镁合金PLC效应的认识还需要从以下5个方面进行深入研究：①随着实验技术的发展，对PLC变形带的空间观察要多样化，发展三维数字成像技术，提高动态观测精度；②研究试件的几何尺寸对锯齿波及变形带的分布、空间形貌、传播特性等的影响；③对动态应变时效微观过程的直接实验观察，动态应变时效是原子位错尺度上伴随变形的动态微观过程，位错的运动和溶质原子气团的形成是关键，可借助透射电镜的附件装置，观察不同成分与处理状态的镁合金在不同加载条件下位错的运动情况，获取动态应变时效的位错运动特点；④孪晶的启动对不同成分与处理状态镁合金PLC效应的影响规律及机理分析；⑤探究抑制镁合金PLC效应的加工工艺或适当的处理方法，改变PLC效应发生的条件，将其转移到材料服役区域以外，以达到抑制PLC效应的效果。

References

[1]Bian Xilei (卞西磊)，Li Jie (李 洁)，Wang Gang (王 刚).MaterialsChina(中国材料进展)[J]，2014，33(5)：265-269.

[2]Luders W．Dingler’sPolytechnischesJournal(Fourth Series)[J]，1860(5)：18-22

[3]Zhemchuzhnikova D A，Lebyodkin M A，Lebedkina T A，etal.MaterialsScience&EngineeringA[J]，2015 (639)：37-41.

[4]Fu S H，Cheng T，Zhang Q C，Qi H，etal.ActaMaterialia[J]，2012(60)：6650-6656.

[5]Cai Y L，Tian C G，Fu S H，etal.MaterialsScience&EngineeringA[J]，2015(638)：314-321.

[6]Maj P，Zdunek J，Gizynski M，etal.MaterialsScience&EngineeringA[J]，2014 (619)：158-164.

[7]Xu Daokui(许道奎)，Li Chuanqiang(李传强)，Han Eenhou(韩恩厚)，etal.MaterialsChina(中国材料进展)[J]，2016，35(3)：146-153.

[8]Yin Miao(尹 淼).DissertationforMasterate(硕士论文)[D].Shenyang：Shenyang Aerospace University，2013.

[9]Zu Tingting(祖婷婷).DissertationforMasterate(硕士论文)[D].Beijing：University of Science and Technology Beijing，2013.

[10]Li C Q，Xu D K，Zu T T，etal.JournalofMagnesiumandAlloys[J]，2015(3)：106-111.

[11]Portevin A，Le Chatelier F.ComptesRendusdeI'AcadémieSciences[J]，1923(176)：507-510.

[12]Rodriguez P.Bull.MaterialsScience[J],1984，6(4)：653-663.

[13]Xu Y B，Xu D K，Shao X H，etal.ActaMetallSin(EnglLett)[J]，2013，26(3)：217-231.

[14]Xu D K，Han E H.ProgressinNaturalScience：MaterialsInternational[J]，2012，22(5)：364-385.

[15]Xu D K，Liu L，Xu Y B，etal.ActaMaterialia[J]，2008(56)：985-994.

[16]Couling S L.ActaMetallurgiea[J]，1959 (7)：133-134.

[17]Keni K G，Kelly A.JournaloftheJapanInstituteofMetals[J]，1965 (93)：536-542.

[18]Geiselman D，Guy A G.TransactionsoftheMetallurgicalSocietyofAIME[J]，1959 (215)：814-820.

[19]Chiao W F，Gordon R B.TransactionsoftheMetallurgicalSocietyofAIME[J]，1966 (236)：658-663.

[20]Koss D A，Gordon R B.TransactionsoftheMetallurgicalSocietyofAIME[J]，1966 (236)：1185-1193.

[21]Huseby I C，Hsu S E，Mcnelley T R，etal.MetallurgicalandMaterialsTransactionsA[J]，1975，6 (11)：2005-2008.

[22]Koike J，Kobayashi T，Mukai T，etal.ActaMaterialia[J]，2003 (51)：2055-2065.

[23]Agnew S R，Horton J A，Lillo T M，etal.ScriptaMaterialia[J]，2004 (50)：377-381.

[24]Mora E，Garces G，Onorbe E，etal.ScriptaMaterialia[J]，2009，60 (9)：776-782.

[25]Chen Lijia(陈立佳)，Mao Liang(茆 亮)，Zhang Siqian(张思倩)，etal.JournalofShenyangUniversityofTechnology(沈阳工业大学学报)[J]，2008，30 (4)：419-423.

[26]Stanford N，Sabirov I，Sha G，etal.MetallurgicalandMaterialsTransactionsA[J]，2010 (41A)：734-743.

[27]Wang C，Li Z Q，Xu Y B，etal.JournalofMaterialsScience[J]，2007 (42)：3573-3579.

[28]Wang C，Xu Y B，Li Z Q，etal.MaterialsLetters[J]，2006 (60)：2941-2944.

[29]Wang Cong(王 聪)，Xu Yongbo(徐永波)，Han Enhou(韩恩厚).ActaMetallurgicaSinica(金属学报)[J]，2006，42 (2)：191-194.

[30]Cai X C，Fu H，Guo J X，etal.MetallurgicalandMaterialsTransactionsA[J]，2014 (45A)：3703-3707.

[31]Zhu S M，Nie J F.ScriptaMaterialia[J]，2004 (50)：51-55.

[32]Wu D，Chen R S，Han E H.MaterialsScienceandEngineeringA[J]，2012 (532)：267-274.

[33]Wu D，Chen R S，Ke W.MaterialsandDesign[J]，2014 (58)：324-331.

[34]Stanford N，Sha G，Xia J H，etal.ScriptaMaterialia[J]，2011 (65)：919-921.

[35]Peng Q，Fu H，Xiao W L.MetallurgicalandMaterialsTransactionsA[J]，2013 (44A)：4469-4474.

[36]Sha G Y，Liu T，Yu T，etal.ProcediaEngineering[J]，2012 (27)：1216-1221.

[37]Trojanova Z，Caceresb C H.ScriptaMaterialia[J]，2007 (56)：793-796.

[38]Cai M C，Niu L S，T.Yu，etal.MaterialsScienceandEngineeringA[J]，2010 (527)：5175-5180.

[39]Wang W H，Wu D，Shah S S A，etal.MaterialsScience&EngineeringA[J]，2016 (649)：214-221.

[40]Azzeddine H，Bradai D.JournalofRareEarths[J]，2013，31 (8)：804-810.

[41]Wang Y，Zhang X N，Cao N Z，etal.JournalofMaterialsScience[J]，2007 (42)：2630-2632.

[42]Qiu W，Han E H，Liu L.JournalofMaterialsScienceandTechnology[J]，2009 (25)：441-444.

[43]Hidalgo-Manrique P，Herrera-Solaz V，Segurado J，etal.ActaMaterialia[J]，2015 (92)：265-277.

[44]Feng F，Huang S Y,Meng Z H，etal.MaterialsandDesign[J]，2014 (57)：10-20.

[45]Dudamell N V，Hidalgo-Manrique P，Chakkedath A，etal.MaterialsScience&EngineeringA[J]，2013 (583)：220-231.

[46]Caceres C H，Rovera D M.JournalofLightMetals[J]，2001 (1-3)：151-156.

[47]Akhtar A，Teghtsoonian E.ActaMetallurgical[J]，1969 (17)：1351-1356.

[48]Lukac P，Czech.JournalofPhysics[J],1981(B31)：130-132.

[49]Gao L，Chen R S，Han E H.JournalofAlloysandCompounds[J]，2009 (472)：234-240.

[50]Xu D K，Li C Q，Wang B J，etal.MaterialsandDesign[J]，2015 (88)：88-97.

[51]Xu D K，Wang B J，Li C Q，etal.MaterialsandDesign[J]，2015 (69)：124-129.

[52]Xu D K，Han E H.ScriptaMaterialia[J]，2014 (71)：21-24.

[53]Xu D K，Zu T T，M Yin，etal.JournalofAlloysandCompounds[J]，2014 (582)：161-166.

[54]Xu D K，Liu L，Xu Y B，etal.ScriptaMaterialia[J]，2007 (57)：285-288.

[55]Nayeb-Hashemi A A，Clark J B.BulletinofAlloyPhaseDiagrams[J]，1984 (5)：365-374.

[56]Gasior W，Moser Z，Zakulski W，etal.MetallurgicalandMaterialsTransactionsA[J]，1996 (27A)：2419-2428.

[57]Wu S K，Chien C，Yang C S，etal.MaterialsScience&EngineeringA[J]，2014 (605)：33-38.

[58]Li Tingqu(李廷取)，Liu Xiangling(刘祥玲)，Meng Fanyan(孟凡岩)，etal.JournalofJilinInstituteofChemicalTechnology(吉林化工学院学报)[J]，2013，30 (11)：59-61.

[59]Li T Q，Liu Y B，Cao Z Y，etal.JournalofAlloysandCompounds[J]，2011 (509)：7607-7601.

[60]Wang C，Xu Y B，Han E H.JournalofMetallurgy[J],2012：1-5.

[61]Qian Kuangwu(钱匡武)，Li Xiaoqi(李效琦)，Xiao Lingang(萧林钢)，etal.JournalofFuzhouUniversity(NaturalScience)(福州大学学报(自然科学版))[J]，2001，29 (6)：8-23.

[62]Fang Xiya(方西亚).ThesisforDoctorate(博士论文)[D].Changsha：Central South University，2009.

[63]Hassan S F.MaterialsScienceandEngineeringA[J]，2011 (528)：5484-5490.

(编辑 吴 琛)

Research Progress on the Plastic Instability Phenomenon of Magnesium Alloys

LI Chuanqiang1,2，XU Daokui2，HAN Enhou2

(1.School of Materials Science and Engineering,Northeastern University,Shenyang 110819,China)(2.CAS Key Laboratory of Nuclear Materials Safety Assessment,Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,China)

Among all the structural metallic materials,magnesium alloys have the lowest density,relatively high specific strength and rigidity.However,under plastic deformation conditions,magnesium alloys can exhibit the phenomenon of plastic instability,i.e.serrated flow or Portevin-Le Chatelier (PLC)effect,showing serrated waves on the stress-strain curves.Recently,research works about the PLC effects of magnesium alloys are widely carried out and increase annually.This paper is mainly concentrated on the research progress on PLC effect of magnesium alloys.The occurring conditions of PLC effect,characteristics of serration,effect of alloying elements on the PLC effect and relevant mechanisms are reviewed.Finally,the existing problems in current studies,research emphasis and direction in the future are also pointed out.

magnesium alloys; Portevin-Le Chatelier effect; serrated flow; deformation mechanism；microstructure

2015-10-19

国家重点研发计划资助项目(2016YFB0700505)；国家重点研发计划课题(2016YFB0301105)；科技部973项目(2013CB632205)

李传强，男，1988年生，博士研究生

许道奎，男，1980年生，教授，博士生导师，Email:dkxu@imr.ac.cn

10.7502/j.issn.1674-3962.2016.11.01

TG146.22

A

1674-3962(2016)11-0809-10