基于KPCA的监控系统传感器异常诊断方法*

彭红星， 潘梨莉， 赵鸿图

(1.河南理工大学 计算机科学与技术学院，河南 焦作 454000；2.煤炭安全生产河南省协同创新中心，河南 焦作 454000)



基于KPCA的监控系统传感器异常诊断方法*

彭红星1，2， 潘梨莉1， 赵鸿图1

(1.河南理工大学 计算机科学与技术学院，河南 焦作 454000；2.煤炭安全生产河南省协同创新中心，河南 焦作 454000)

针对监控系统数据异常时，故障检测准确性不高的问题，提出一种基于监控系统传感器异常的核主元分析(KPCA )检测方法。利用平方预报误差(SPE)统计量和均方贡献值法进行故障检测和故障源的定位，改善了主元分析(PCA)应用于非线性系统故障检测准确性低的问题。分别利用基于KPCA和PCA的故障检测模型进行仿真比较。实验结果表明：KPCA提高了非线性监控系统传感器异常诊断的准确性。

传感器； 核主元分析； 主元分析； 故障检测； 故障源定位

0 引 言

瓦斯抽采监控系统是由大量传感器组成，大部分传感器都处于高湿度、高压等恶劣环境下，容易造成传感器性能下降且大多数传感器不具备自我诊断和校正功能。因此，需要人工定期校准，但两次人工校准期间无法掌握测量数据的准确度，针对这一问题，文献[1]提出了基于概率鲁棒思想的自适应阈值算法，但该算法忽略了多个传感器之间的关联性，不能准确预测故障的发生，因此，需要一种更加有效的方法来监测故障。故障诊断方法很多[2]，但由于复杂的瓦斯抽采监控系统无法得到精确的解析式，而基于信号处理的主元分析(PCA)方法不需要建立系统的数学模型，因而其成为一种很好的故障检测方法。

PCA是一种线性诊断方法，在很多领域得到了广泛应用，且取得了一定的研究成果[3～6]。复杂的瓦斯抽采监控系统不存在严格的线性关系，因此，将PCA直接运用于监控系统可能会产生较大的偏差。另外，由于PCA直接舍弃特征值较小的主元，若运用PCA监控系统有可能较小的主元包含重要的信息。所以，需寻找更合适的建模方法来解决复杂的瓦斯抽采监控系统数据诊断问题。

针对上文中PCA方法的局限性，Scholkopf B等人提出了一种基于核主元分析(kernel PCA,KPCA)的非线性故障诊断方法[7]，Lee Jong-Min等人已证明KPCA方法在非线性故障监测方面具有一定优势[8]。本文运用KPCA建立瓦斯抽采监控系统模型进行故障检测，并利用均方贡献值法进行故障源定位。通过仿真实验比较KPCA和PCA的故障检测效果，实验结果表明KPCA故障检测的准确性和可靠性高于PCA。

1 KPCA

1.1 KPCA检测模型

(1)

设相关矩阵R的特征值和特征向量分别为λ和v,则有

Rv=λv

(2)

由于等式

(3)

存在系数ai(i=1,2,…,m)，使得特征向量v必定在特征点φ(xi)的张成平面内，即v表示为

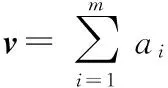
(4)

式中 m维矢量a，它的第j个元素是系数aj。

引入矩阵K是m×m维的核矩阵，其定义为

K=k(xi,xj)={kij}=(φ(xi),φ(xj)),

i,j=1,2,…,m

式中 kij为核函数K的第i行第j列元素。

将式(4)代入式(3)且两边左乘φ(xk)，得

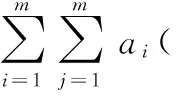
i,j,k=1,2,…,m

(5)

根据引入的矩阵，式(5)化简式得：mλa=Ka。

求解上式，得出矩阵K的特征值是mλi,(规定λ1≥λ2≥…≥λm)且与其对应的特征向量ai(i=1,2,…，m)。其中，向量a归一化可通过相关矩阵R的特征向量v的归一化来实现。

测试样本数据的第s个非线性主元ts的提取[7]可表示为

(6)

式中vs为相关矩阵R的第 个特征向量；as,i为核矩阵K的第k个特征值对应的特征向量as的第i个系数。

1.2 KPCA归一化处理

PCA一般运用主元贡献率来确定主元个数。同样，KPCA经过映射后，在特征空间中也应用主元贡献率来确定主元个数。

2 故障检测与分离

2.1 基于KPCA的故障检测

故障检测方法很多，基于霍金斯指标的故障检测[9]适用于传感器个数相对比较少的情况下，基于T2指标的故障检测[10]灵敏度不高，而基于平方预报误差(square prediction error,SPE)统计量[11]简单、准确度高，所以,本文运用SPE统计量进行故障检测。

由于测量变量之间的非线性，所以，这就需要一种基于KPCA的故障检测方法。数据经过非线性映射到特征空间后，在特征空间中运用SPE统计量进行故障检测，其定义[11]如下式

(7)

SPE统计量的控制限可以由其适当的估计分布进行计算如下

(8)

式中g为表征SPE幅值的权重参数，h为χ2分布的自由度。假设a和b分别为KPCA建模样本中SPE的估计均值与方差，则g和h计算如下

(9)

2.2 基于KPCA的故障源定位

由于KPCA的非线性变换函数不是显式表示，所以,需要通过分析可知故障变量与非线性主元之间的关系强，正常变量与非线性主元之间的关系弱。

本文在基于KPCA贡献图的基础上，借鉴T2统计量的计算原理，定义第i个测量变量xi的均方贡献值如下

(10)

则新的测量向量的均方贡献向量C计算过程如下

C′=xTtΛ-1

(11)

上式每行的范数即为每个测量变量的均方贡献值，故令

(12)

C=[c1c2…cn]T

(13)

3 仿真实验研究

3.1 模型建立

以郑煤集团某泵站监控系统为研究对象，监控系统中包括多个传感器对不同高度的支管道和主管道的瓦斯浓度、流量、和压力等参数连续监测。本文选取以上200组监测参数作为建立模型的数据源，部分传感器测点如表1。

表1 传感器与测点位置

3.2 故障检测实验

选取正常状态下的样本数据，根据基于KPCA所建立的模型计算SPE值和阈值。如果所有传感器均正常，则SPE值小于阈值。以Fwj流量传感器为例，其效果如图1。

图1 基于KPCA各传感器正常工作时的检测结果Fig 1 Detection results of each sensor in normaloperation based on KPCA

3.2.1 20 %故障检测实验

另选取200组样本数据，在流量传感器Fwj信号的第120点数据加上20 %阶跃信号来模拟基于KPCA和PCA的故障检测效果，其结果如图2和图3所示。

图2 基于PCA的传感器故障检测Fig 2 Sensor fault detection based on PCA

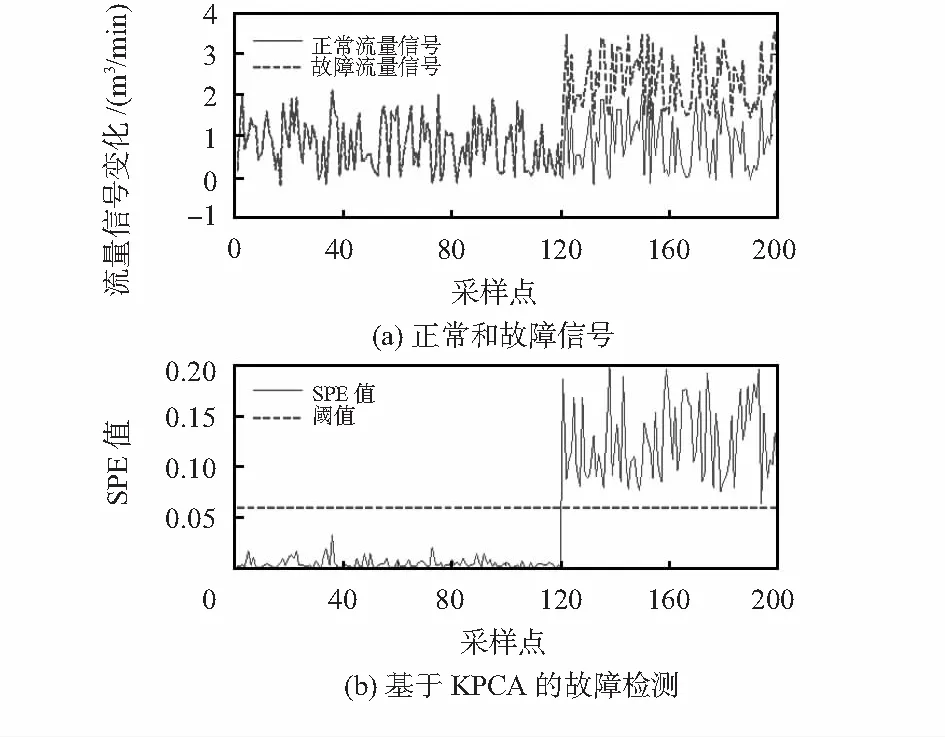
图3 基于KPCA的传感器故障检测Fig 3 Sensor fault detection based on KPCA

图2(a)和图3(a)为Fwj正常信号和模拟故障信号的比较，故障从第120～200个采样点。由图2(b)和图3(b)可知，在第120～200个采样点，SPE值都明显超出其阈值，其他采样点都在阈值下，说明基于KPCA和PCA方法都检测出了故障。

3.2.2 小故障检测实验

采用上述的200组样本数据，在第120～200个采用数据点加上10 %信号来模拟基于KPCA和PCA的故障检测效果，其结果如图4和图5所示。

图4 基于PCA的小故障检测Fig 4 Small fault detection based on PCA

图5 基于KPCA的小故障检测Fig 5 Small fault detection based on KPCA

同样，图4(a)和图5(a)为Fwj正常信号和模拟故障信号的比较。较图2(a)和图3(a)可知，图4(a)和图5(a)的正常信号与故障信号的偏离幅度不明显，其原因为小故障。由图4(b)和图5(b)可知，在第120～200个采样点，观察图4(b)，故障信号的SPE值高于其正常信号的SPE值但都低于其阈值。由图5(b)可知，故障信号的SPE值高于其阈值，其他正常信号点都在阈值以下。说明基于KPCA方法检测出了小故障，而基于PCA方法无法准确检测出非严格线性关系系统的小故障。

文中运用均方贡献值法进行故障分离，由图6看出，随机选取的4个样本点都检测出第3只流量传感器发生了故障，很好地验证了基于KPCA方法故障检测的高效性。

图6 基于KPCA方法的传感器故障分离Fig 6 Sensor fault isolation based on KPCA

4 结 论

本文以郑煤集团某泵站监控系统为例，对基于KPCA和PCA的故障检测方法进行了验证比较。通过仿真实验得出，对于非严格线性关系的系统，基于KPCA方法的故障检测优于基于PCA方法的故障检测。检测到故障后，利用均方贡献值法进行故障源定位。实验结果表明：基于KPCA的故障检测和识别方法对非严格线性关系的监控系统具有很好的应用意义。

[1] 李 楠，张云燕,，李言俊.一种自旋稳定卫星姿态传感器数据异常的诊断方法[J].宇航学报，2011，32(6)：1327-1332.

[2] 马文龙，吕建新，吴虎胜，等.多传感器信息融合在滚动轴承故障诊断中的应用[J].传感器与微系统，2013，32(7)：132-135.

[3] 梁冠东，郭 栋，彭红星.压风机监控系统传感器故障检测与分离方法[J].煤炭科学技术，2011，39(6)：82-85.

[4] 邓晓刚，田学民.一种基于KPCA的非线性故障诊断方法[J].山东大学学报：工学版，2005(3)：103-106.

[5] 李冬辉，王乐英，李 晟.基于PCA的空调系统传感器故障诊断[J].电工技术学报，2008(6)：130-136.

[6] 王巍巍，张赛男.基于PCA与BP混合神经网络算法的电子鼻系统[J].传感器与微系统， 2014，33(4)：90-92.

[7] Scholkopf B,Smola A,Muller K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5):1299-1319.

[8] Lee Jong-Min,Yoo Chang-Kyoo,Choi Sang-Wook,et al.Nonlinear process monitoring using kernel principal component analysis[J].Chemical Engineering Science,2004,59(1):223-234.

[9] 邱 天，丁艳军，吴占松.基于霍金斯指标的传感器数据有效性验证[J].中国电机工程学报，2007，27(14)：77-81.

[10] 许 洁,胡寿松,申忠宇.基于改进多尺度核主元分析的化工过程故障检测与诊断方法研究[J].仪器仪表学报,2010，31(1)：51-55.

[11] Peng H X,Wang R,Hai L P.Sensor fault detection and identification using Kernel PCA and its fast data reconstruction[C]∥2010 Chinese Control and Decision Conference,CCDC 2010,Xuzhou,China,2010:26-28.

Study on abnormal diagnosis of sensor in monitoring system based on KPCA*

PENG Hong-xing1,2, PAN Li-li1, ZHAO Hong-tu1

(1.School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China; 2.Collaborative Innovation Center of Coal Work Safety，Jiaozuo 454000,China)

Aiming at problem of low accuracy of fault detection when abnormal data occurs in monitoring system,put forward a detecting method of kernel principal component analysis(KPCA),which is based on sensor abnormal of monitoring system.The method KPCA detects faults and locates the fault source via the statistics of square prediction error(SPE)and the mean square contribution value from KPCA method,improve problem of low accuracy of PCA applied to fault detecting of nonlinear system.Fault detecting models based on KPCA and PCA are used for simulation and comparison.Experimental results show that KPCA improve accuracy of sensor abnormal diagnosis of nonlinear monitoring system.

sensor; kernel principal component analysis(KPCA); PCA; fault detection; fault source identification

10.13873/J.1000—9787(2016)12—0033—04

2016—01—27

煤炭安全生产河南省协同创新中心重点资助项目(12140024)； 河南理工大学博士基金资助项目(64998449)

TP 712

A

1000—9787(2016)12—0033—04

彭红星(1977-)，男，河南滑县人，博士，副教授，主要从事安全检测与监控，信号处理与模式识别方向研究工作。