处理含参函数问题的常用策略———从一道模拟题的多种解法谈起

金国林

(浙江省宁波市镇海中学，315200)



处理含参函数问题的常用策略
———从一道模拟题的多种解法谈起

金国林

(浙江省宁波市镇海中学，315200)

自导数进入高中课堂后,以函数为载体,导数为工具的含参函数问题便纷纷出现在各省、市的高考试卷中.含参问题是检测学生逻辑理解能力和分析能力的一种综合题型.运用导数确定参数的取值范围是其中一类常见的探索性问题,是函数与导数交汇试题的显著特点和命题趋向.笔者以最近碰到的一道模拟题的多种解法为例,谈谈解决此类问题的几种常见思路,以飨读者.

题目 已知函数f(x)=x2+2x+aln x,对于任意的t≥1恒有f(2t-1)≥2f(t)-3.求实数a的取值范围.

一、单边化零法

解法1 根据题意,通过代入化简,原问题的条件等价于:对于任意的t≥1,不等式

2(t-1)2+aln(2t-1)-2aln t≥0

恒成立.令u(t)=2(t-1)2+aln(2t-1)-2aln t,则

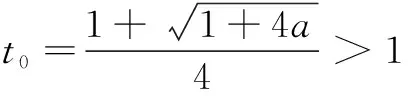
评注 将相关变量全部移到不等式一边后直接利用导数来研究函数性质,再对参数进行分类讨论是解决此类问题的基本方法.此种方法起点低,入手容易,经常需要进行累次求导,关键是要找准参数的分界值,这是个难点.

二、分离变量法

解法2 问题等价于对任意的t≥1,不等式

2(t-1)2≥a[2ln t-ln(2t-1)]

恒成立；当t=1时,不等式对于任意实数a恒成立.当t>1时,由于2ln t>ln(2t-1),故问题等价于对任意的t>1,

恒成立.

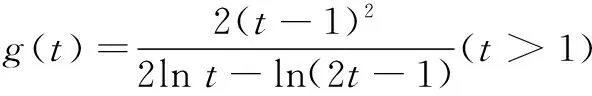
即h(t)在(1,+∞)内为增函数,故h(t)>h(1)=0，从而g′(t)>0,即g(t)在(1,+∞)内为增函数.根据洛必达法则,有

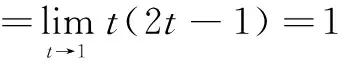
故满足条件的实数a的取值范围为a≤2.

评注 利用分离变量来处理此类问题也是一种非常基本的想法,而且在很多问题中往往能见奇效.通过分离变量,明确目标函数,能在一定程度上避免分类讨论带来的繁杂.这种方法在处理边界值时需要特别注意,它经常需要利用洛必达法则求极限值,这超出了高中数学的内容范围,需要谨慎选择.

三、构造统一函数

解法3 事实上,我们可以将解法2中的不等式

2(t-1)2≥a[2ln t-ln(2t-1)]

恒等变形为

2t2-aln t2≥2(2t-1)-aln(2t-1).

构造函数h(x)=2x-aln x (x≥1).

由于t2≥2t-1,且t为大于等于1的任意实数,因此我们只需考虑h(x)在(1,+∞)内为增函数即可.

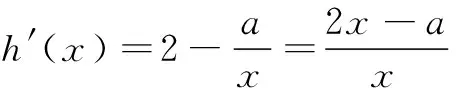
故 a≤2.

综上,实数a取值范围为a≤2.

评注 解法3针对题中系数结构特点,将原式进行大胆地恒等变形,构造一个全新的含参函数进行处理,有拨开云雾见青天之效.不过，虽然此种解法非常巧妙,但不是解决含参问题的基本方法.

四、利用不等式放缩

解法4 进一步,我们可以将解法2中的“对任意的实数t>1时,

恒成立”恒等变形为对任意的实数t>1,

恒成立.

当t>1时,利用不等式ln(1+x)≤x,有

从而实数a的取值范围是a≤2.

评注 利用熟悉的不等式进行局部放缩也是一种非常重要的方法.解法4将不等式ln(1+x)≤x运用得非常巧妙,直接将对数函数放缩成一个多项式函数,问题立刻得到解决.

五、利用函数的凹凸性

解法5 通过仔细观察,我们能够发现f(1)=3,故原问题等价于

对于任意t≥1恒成立.

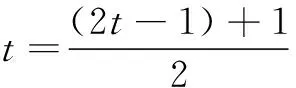
评注 解法5站在更高的观点下对问题进行宏观考虑,从整体上把握函数的本质属性,也是本题的命制背景.

尽管含参函数问题综合性强,但只要我们认真审题,深入挖掘变量关系,以单边化零或分离变量法为根本,基本能解决一般的含参问题.当然,如果我们能根据问题的特性,多思考尝试不等式放缩、构造统一函数等其他方法,也许能发现更巧妙的方法,收获意外的惊喜.